Table of contents

15 March 2014, Volume 23 Issue 3 Previous issue    Next issue

GENERAL

Select

Lie group analysis, numerical and non-traveling wave solutions for the (2+1)-dimensional diffusion–advection equation with variable coefficients Vikas Kumar, R. K. Gupta, Ram Jiwari Chin. Phys. B, 2014, 23 (3):  030201.  DOI: 10.1088/1674-1056/23/3/030201 Abstract ( 744 )   PDF (402KB) ( 511 )   In this paper, the variable-coefficient diffusion-advection (DA) equation, which arises in modeling various physical phenomena, is studied by the Lie symmetry approach. The similarity reductions are derived by determining the complete sets of point symmetries of this equation, and then exact and numerical solutions are reported for the reduced second-order nonlinear ordinary differential equations. Further, an extended (G’/G)-expansion method is applied to the DA equation to construct some new non-traveling wave solutions.

Select

Elastic behavior of disclination dipole near nanotube with surface/interface effect Zhao Ying-Xin (赵迎新), Zeng Xin (曾鑫), Chen Chang-Ping (陈昌萍) Chin. Phys. B, 2014, 23 (3):  030202.  DOI: 10.1088/1674-1056/23/3/030202 Abstract ( 596 )   PDF (761KB) ( 498 )   In this paper, we present an analytical solution of the interaction of the nanotube (NT) with a wedge disclination dipole in nanotube-based composites. The corresponding boundary value problem is solved exactly by using complex potential functions. The explicit expression of the force exerted on disclination dipole is given by using the generalized Peach–Koehler formula. As a numerical illustration, both the equilibrium position and the stability of the disclination dipole are evaluated for different material combinations, relative thickness of an NT, surface/interface effects, and the features of the disclination dipole. The results show that as the thickness of the NT layer increases, the NT has a relatively major role in the force acting on the disclination dipole in the NT-based composite. The cooperative effect of surface/interface stresses and the NT becomes considerable as the increase of NT layer thickness. The equilibrium position may occur, even more than one, due to the influences of the surface/interface stress and the NT thickening. The influences of the surface/interface stresses and the thickness of the NT layer on the force are greatly dependent on the disclination angle.

Select

Second-order two-scale computations for conductive–radiative heat transfer problem in periodic porous materials Yang Zhi-Qiang (杨志强), Cui Jun-Zhi (崔俊芝), Li Bo-Wen (李博文) Chin. Phys. B, 2014, 23 (3):  030203.  DOI: 10.1088/1674-1056/23/3/030203 Abstract ( 578 )   PDF (6432KB) ( 445 )   In this paper, a kind of second-order two-scale (SOTS) computation is developed for conductive–radiative heat transfer problem in periodic porous materials. First of all, by the asymptotic expansion of the temperature field, the cell problem, homogenization problem, and second-order correctors are obtained successively. Then, the corresponding finite element algorithms are proposed. Finally, some numerical results are presented and compared with theoretical results. The numerical results of the proposed algorithm conform with those of the FE algorithm well, demonstrating the accuracy of the present method and its potential applications in thermal engineering of porous materials.

Select

A new explicit multisymplectic integrator for the Kawahara-type equation Cai Wen-Jun (蔡文君), Wang Yu-Shun (王雨顺) Chin. Phys. B, 2014, 23 (3):  030204.  DOI: 10.1088/1674-1056/23/3/030204 Abstract ( 624 )   PDF (728KB) ( 713 )   We derive a new multisymplectic integrator for the Kawahara-type equation which is a fully explicit scheme and thus needs less computation cost. Multisympecticity of such scheme guarantees the long-time numerical behaviors. Numerical experiments are presented to verify the accuracy of this scheme as well as the excellent performance on invariant preservation for three kinds of Kawahara-type equations.

Select

Dissipative preparation of a steady three-dimensional entangled state via quantum-jump-based feedback Chen Li (陈丽), Wang Hong-Fu (王洪福), Zhang Shou (张寿) Chin. Phys. B, 2014, 23 (3):  030301.  DOI: 10.1088/1674-1056/23/3/030301 Abstract ( 561 )   PDF (1542KB) ( 382 )   A robust and scalable scheme to generate a steady three-dimensional entangled state for a V-type atom and a Λ-type atom trapped in a strongly dissipative bimodal cavity is proposed by direct feedback control based on quantum-jump detection. The robustness of this scheme reflects in the insensitivity to detection inefficiencies and the strong ability against the parameter fluctuations in the feedback, driving, and coupling strengths. The influence of atomic spontaneous emission can be suppressed by using the local feedback control. The scalability is ensured that N-dimensional entangled states of two atoms can be deterministically generated.

Select

Averaging in SU(2) open quantum random walk Clement Ampadu Chin. Phys. B, 2014, 23 (3):  030302.  DOI: 10.1088/1674-1056/23/3/030302 Abstract ( 648 )   PDF (783KB) ( 350 )   We study the average position and the symmetry of the distribution in the SU(2) open quantum random walk (OQRW). We show that the average position in the central limit theorem (CLT) is non-uniform compared with the average position in the non-CLT. The symmetry of distribution is shown to be even in the CLT.

Select

Master equation describing the diffusion process for a coherent state Liu Tang-Kun (刘堂昆), Shan Chuan-Jia (单传家), Liu Ji-Bing (刘继兵), Fan Hong-Yi (范洪义) Chin. Phys. B, 2014, 23 (3):  030303.  DOI: 10.1088/1674-1056/23/3/030303 Abstract ( 588 )   PDF (186KB) ( 1044 )   The evolution of a pure coherent state into a chaotic state is described very well by a master equation, as is validated via an examination of the coherent state’s evolution during the diffusion process, fully utilizing the technique of integration within an ordered product (IWOP) of operators. The same equation also describes a limitation that maintains the coherence in a weak diffusion process, i.e., when the dissipation is very weak and the initial average photon number is large. This equation is dρ/dt=-κ[a+aρ-a+ρa-aρa++ρaa+]. The physical difference between this diffusion equation and the better-known amplitude damping master equation is pointed out.

Select

Evolution law of a negative binomial state in an amplitude dissipative channel Chen Feng (陈锋), Fan Hong-Yi (范洪义) Chin. Phys. B, 2014, 23 (3):  030304.  DOI: 10.1088/1674-1056/23/3/030304 Abstract ( 631 )   PDF (169KB) ( 361 )   For the first time we derive the evolution law of the negative binomial state  in an amplitude dissipative channel with a damping constant κ. We find that after passing through the channel, the final state is still a negative binomial state, however the parameter γ evolves into γ’, where γ’=γ/(e-2κt(1-γ)+γ). The decay law of the average photon number is also obtained.

Select

Mutual transformations between the P–Q,Q–P, and generalized Weyl ordering of operators Xu Xing-Lei (徐兴磊), Li Hong-Qi (李洪奇), Fan Hong-Yi (范洪义) Chin. Phys. B, 2014, 23 (3):  030305.  DOI: 10.1088/1674-1056/23/3/030305 Abstract ( 632 )   PDF (198KB) ( 415 )   Based on the generalized Weyl quantization scheme, which relies on the generalized Wigner operator Ωk(p,q) with a real k parameter and can unify the P–Q, Q–P, and Weyl ordering of operators in k=1,-1,0, respectively, we find the mutual transformations between δ(p-P)δ(q-Q), δ(q-Q)δ(p-P), and Ωk(p,q), which are, respectively, the integration kernels of the P–Q, Q–P, and generalized Weyl quantization schemes. The mutual transformations provide us with a new approach to deriving the Wigner function of quantum states. The P- and Q- ordered forms of Ωk(p,q) are also derived, which helps us to put the operators into their P- and Q- ordering, respectively.

Select

Bound state solutions of the Dirac equation with the Deng–Fan potential including a Coulomb tensor interaction S. Ortakaya, H. Hassanabadi, B. H. Yazarloo Chin. Phys. B, 2014, 23 (3):  030306.  DOI: 10.1088/1674-1056/23/3/030306 Abstract ( 598 )   PDF (329KB) ( 486 )   Approximate analytical solutions of the Dirac equation in the case of pseudospin and spin symmetry limits are investigated under the Deng–Fan potential by applying the asymptotic iteration method for the arbitrary quantum numbers n and κ. Some of the numerical results are also represented in both pseudospin symmetry and spin symmetry limits.

Select

The duality of a single particle with an n-dimensional internal degree of freedom Jia Ai-Ai (贾爱爱), Huang Jie-Hui (黄接辉), Feng Wei (冯伟), Zhang Tian-Cai (张天才), Zhu Shi-Yao (朱诗尧) Chin. Phys. B, 2014, 23 (3):  030307.  DOI: 10.1088/1674-1056/23/3/030307 Abstract ( 536 )   PDF (641KB) ( 418 )   The wave–particle duality of a single particle with an n-dimensional internal degree of freedom is re-examined theoretically in a Mach–Zehnder interferometer. The famous duality relation D2+V2 ≤ 1 is always valid in this situation, where D is the distinguishability and V is the visibility. However, the sum of the particle information and the wave information, D2+V2, can be smaller than one for the input of a pure state if this initial pure state includes the internal degree of freedom of the particle, while the quantity D2+V2 is always equal to one when the internal degree of freedom of the particle is excluded.

Select

An adiabatic quantum optimization for exact cover 3 problem Zhang Ying-Yu (张映玉), Xu Li-Li (许丽莉), Li Jun-Qing (李俊青) Chin. Phys. B, 2014, 23 (3):  030308.  DOI: 10.1088/1674-1056/23/3/030308 Abstract ( 748 )   PDF (172KB) ( 307 )   A perturbation method is applied to study the structure of the ground state of the adiabatic quantum optimization for the exact cover 3 problem. It is found that the instantaneous ground state near the end of the evolution is mainly composed of the eigenstates of the problem Hamiltonian, which are Hamming close to the solution state. And the instantaneous ground state immediately after the starting is mainly formed of low energy eigenstates of the problem Hamiltonian. These results are then applied to estimate the minimum gap for a special case.

RAPID COMMUNICATION

Select

All-electrically reading out and initializing topological qubits with quantum dots Hot! Chen Wei (陈伟), Xue Zheng-Yuan (薛正远), Wang Z. D.(汪子丹) , Shen Rui (沈瑞) Chin. Phys. B, 2014, 23 (3):  030309.  DOI: 10.1088/1674-1056/23/3/030309 Abstract ( 564 )   PDF (309KB) ( 463 )   We analyze the reading and initialization of a topological qubit encoded by Majorana fermions in one-dimensional semiconducting nanowires, weakly coupled to a single level quantum dot (QD). It is shown that when the Majorana fermions are fused by tuning gate voltage, the topological qubit can be read out directly through the occupation of the QD in an energy window. The initialization of the qubit can also be realized via adjusting the gate voltage on the QD, with the total fermion parity conserved. As a result, both reading and initialization processes can be achieved in an all-electrical way.

GENERAL

Select

Quantum entanglement of an entangled coherent state：Role of particle losses Liu Pan (刘盼), Feng Xiao-Min (冯晓敏), Jin Guang-Ri (金光日) Chin. Phys. B, 2014, 23 (3):  030310.  DOI: 10.1088/1674-1056/23/3/030310 Abstract ( 691 )   PDF (892KB) ( 558 )   We analyze entanglement properties of entangled coherent state (ECS), |α, 0>1,2+|0, α >1,2, with and without photon losses. 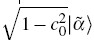By separating the coherent state into |α >=c0|0>+, we derive exact results of the logarithmic negativity EN, which quantifies the degree of entanglement between the two bosonic modes. Without particle losses, EN=1 for the N00N state; while for the ECS, EN increases from 0 to 1 as |α|2→∞. In the presence of photon losses, we find that the ECS with large enough photon number is more robust than that of the N00N state. An optimal ECS is obtained by maximizing EN with respect to |α|2.

Select

Soliton breathers in spin-1 Bose–Einstein condensates Ji Shen-Tong (冀慎统), Yan Pei-Gen (颜培根), Liu Xue-Shen (刘学深) Chin. Phys. B, 2014, 23 (3):  030311.  DOI: 10.1088/1674-1056/23/3/030311 Abstract ( 564 )   PDF (1258KB) ( 494 )   We consider a spin-1 Bose–Einstein condensate trapped in a harmonic potential with different nonlinearity coefficients. We illustrate the dynamics of soliton breathers in two-component and three-component states by numerically solving the one-dimensional time-dependent coupled Gross–Pitaecskii equations (GPEs). We present that two condensates with repulsive interspecies interactions make elastic collision and novel soliton breathers are created in two-component state. We also demonstrate novel soliton breathers in three-component state with attractive coupling constants. Furthermore, possible reasons for creating soliton breathers are discussed.

Select

Exact breathing soliton solutions in combined time-dependent harmonic-lattice potential You Lu-Yun (佑六云), Li Hua-Mei (李画眉), He Jun-Rong (何俊荣) Chin. Phys. B, 2014, 23 (3):  030501.  DOI: 10.1088/1674-1056/23/3/030501 Abstract ( 502 )   PDF (1796KB) ( 460 )   We investigate the explicit novel localized nonlinear matter waves of the cubic-quintic nonlinear Schrödinger equation with spatiotemporal modulation of the nonlinearities and the harmonic-lattice potential using a modified similarity transformation. We also find that when the modulus of the Jacobian elliptic function in the limit closes to 1, the shapes of the breathing solitons may exhibit some interesting features, i.e., one breathing soliton dividing into two in the ground state. The stability of the exact solutions is investigated numerically such that some stable breathing soliton solutions are found.

Select

A modified fractional least mean square algorithm for chaotic and nonstationary time series prediction Bilal Shoaib, Ijaz Mansoor Qureshi, Ihsanulhaq, Shafqatullah Chin. Phys. B, 2014, 23 (3):  030502.  DOI: 10.1088/1674-1056/23/3/030502 Abstract ( 785 )   PDF (340KB) ( 898 )   A method of modifying the architecture of fractional least mean square (FLMS) algorithm is presented to work with nonlinear time series prediction. Here we incorporate an adjustable gain parameter in the weight adaptation equation of the original FLMS algorithm and absorb the gamma function in the fractional step size parameter. This approach provides an interesting achievement in the performance of the filter in terms of handling the nonlinear problems with less computational burden by avoiding the evaluation of complex gamma function. We call this new algorithm as the modified fractional least mean square (MFLMS) algorithm. The predictive performance for the nonlinear Mackey glass chaotic time series is observed and evaluated using the classical LMS, FLMS, kernel LMS, and proposed MFLMS adaptive filters. The simulation results for the time series with and without noise confirm the superiority and improvement in the prediction capability of the proposed MFLMS predictor over its counterparts.

Select

A fast image encryption algorithm based on only blocks in cipher text Wang Xing-Yuan (王兴元), Wang Qian (王倩) Chin. Phys. B, 2014, 23 (3):  030503.  DOI: 10.1088/1674-1056/23/3/030503 Abstract ( 614 )   PDF (4231KB) ( 646 )   In this paper, a fast image encryption algorithm is proposed, in which the shuffling and diffusion is performed simultaneously. The cipher-text image is divided into blocks and each block has k×k pixels, while the pixels of the plain-text are scanned one by one. Four logistic maps are used to generate the encryption key stream and the new place in the cipher image of plain image pixels, including the row and column of the block which the pixel belongs to and the place where the pixel would be placed in the block. After encrypting each pixel, the initial conditions of logistic maps would be changed according to the encrypted pixel’s value; after encrypting each row of plain image, the initial condition would also be changed by the skew tent map. At last, it is illustrated that this algorithm has a faster speed, big key space, and better properties in withstanding differential attacks, statistical analysis, known plaintext, and chosen plaintext attacks.

Select

Periodic synchronization of community networks with non-identical nodes uncertain parameters and adaptive coupling strength Chai Yuan (柴元), Chen Li-Qun (陈立群) Chin. Phys. B, 2014, 23 (3):  030504.  DOI: 10.1088/1674-1056/23/3/030504 Abstract ( 561 )   PDF (1037KB) ( 403 )   In this paper, we propose a novel approach for simultaneously identifying unknown parameters and synchronizing time-delayed complex community networks with nonidentical nodes. Based on the LaSalle’s invariance principle, a criterion is established by constructing an effective control identification scheme and adjusting automatically the adaptive coupling strength. The proposed control law is applied to a complex community network which is periodically synchronized with different chaotic states. Numerical simulations are conducted to demonstrate the feasibility of the proposed method.

Select

Experimental identification of a comb-shaped chaotic region in multiple parameter spaces simulated by the Hindmarsh–Rose neuron model Jia Bing (贾冰) Chin. Phys. B, 2014, 23 (3):  030505.  DOI: 10.1088/1674-1056/23/3/030505 Abstract ( 716 )   PDF (1185KB) ( 789 )   A comb-shaped chaotic region has been simulated in multiple two-dimensional parameter spaces using the Hindmarsh–Rose (HR) neuron model in many recent studies, which can interpret almost all of the previously simulated bifurcation processes with chaos in neural firing patterns. In the present paper, a comb-shaped chaotic region in a two-dimensional parameter space was reproduced, which presented different processes of period-adding bifurcations with chaos with changing one parameter and fixed the other parameter at different levels. In the biological experiments, different period-adding bifurcation scenarios with chaos by decreasing the extra-cellular calcium concentration were observed from some neural pacemakers at different levels of extra-cellular 4-aminopyridine concentration and from other pacemakers at different levels of extra-cellular caesium concentration. By using the nonlinear time series analysis method, the deterministic dynamics of the experimental chaotic firings were investigated. The period-adding bifurcations with chaos observed in the experiments resembled those simulated in the comb-shaped chaotic region using the HR model. The experimental results show that period-adding bifurcations with chaos are preserved in different two-dimensional parameter spaces, which provides evidence of the existence of the comb-shaped chaotic region and a demonstration of the simulation results in different two-dimensional parameter spaces in the HR neuron model. The results also present relationships between different firing patterns in two-dimensional parameter spaces.

Select

Riccati-type Bäcklund transformations of nonisospectral and generalized variable-coefficient KdV equations Yang Yun-Qing (杨云青), Wang Yun-Hu (王云虎), Li Xin (李昕), Cheng Xue-Ping (程雪苹) Chin. Phys. B, 2014, 23 (3):  030506.  DOI: 10.1088/1674-1056/23/3/030506 Abstract ( 670 )   PDF (249KB) ( 625 )   We extend the method of constructing Bäcklund transformations for integrable equations through Riccati equations to the nonisospectral and the variable-coefficient equations. By taking nonisospectral and generalized variable-coefficient Korteweg–de Vries (KdV) equations as examples, their Bäcklund transformations are obtained under a more generalized constrain condition. In addition, the Lax pairs and infinite numbers of conservation laws of these equations are given. Especially, some classical equations such as the cylindrical KdV equation are just the special cases of the constrain condition.

Select

A control method applied to mixed traffic flow for the coupled-map car-following model Cheng Rong-Jun (程荣军), Han Xiang-Lin (韩祥临), Lo Siu-Ming (卢兆明), Ge Hong-Xia (葛红霞) Chin. Phys. B, 2014, 23 (3):  030507.  DOI: 10.1088/1674-1056/23/3/030507 Abstract ( 841 )   PDF (1808KB) ( 534 )   In light of previous work [Phys. Rev. E 60 4000 (1999)], a modified coupled-map car-following model is proposed by considering the headways of two successive vehicles in front of a considered vehicle described by the optimal velocity function. The non-jam conditions are given on the basis of control theory. Through simulation, we find that our model can exhibit a better effect as p=0.65, which is a parameter in the optimal velocity function. The control scheme, which was proposed by Zhao and Gao, is introduced into the modified model and the feedback gain range is determined. In addition, a modified control method is applied to a mixed traffic system that consists of two types of vehicle. The range of gains is also obtained by theoretical analysis. Comparisons between our method and that of Zhao and Gao are carried out, and the corresponding numerical simulation results demonstrate that the temporal behavior of traffic flow obtained using our method is better than that proposed by Zhao and Gao in mixed traffic systems.

REVIEW

Select

Review of chip-scale atomic clocks based on coherent population trapping Wang Zhong (汪中) Chin. Phys. B, 2014, 23 (3):  030601.  DOI: 10.1088/1674-1056/23/3/030601 Abstract ( 805 )   PDF (857KB) ( 2062 )   Research on chip-scale atomic clocks (CSACs) based on coherent population trapping (CPT) is reviewed. The background and the inspiration for the research are described, including the important schemes proposed to improve the CPT signal quality, the selection of atoms and buffer gases, and the development of micro-cell fabrication. With regard to the reliability,stability, and service life of the CSACs, the research regarding the sensitivity of the CPT resonance to temperature and laser power changes is also reviewed, as well as the CPT resonance’s collision and light of frequency shifts. The first generation CSACs have already been developed but its characters are still far from our expectations. Our conclusion is that miniaturization and power reduction are the most important aspects calling for further research.

GENERAL

Select

Optical properties of aluminum-doped zinc oxide films deposited by direct-current pulse magnetron reactive sputtering Gao Xiao-Yong (郜小勇), Chen Chao (陈超), Zhang Sa (张飒) Chin. Phys. B, 2014, 23 (3):  030701.  DOI: 10.1088/1674-1056/23/3/030701 Abstract ( 771 )   PDF (276KB) ( 995 )   A series of <103>-oriented aluminum-doped zinc oxide (AZO) films were deposited on glass substrates via direct-current pulse magnetron reactive sputtering at different O2-to-Ar gas flow ratios (GFRs). The optical properties of the films were characterized using the fitted optical constants in the general oscillator model (which contains two Psemi-Tri oscillators) through the use of measured ellipsometric parameters. The refractive index dispersion data below the interband absorption edge were analyzed using a single-oscillator model. The fitted optical energy gap obtained using the single-oscillator model clearly shows a blue shift, followed by a red shift, as the GFR increases from 0.9/18 to 2.1/18. This shift can be attributed to the change in the free electron concentration of the film, which is closely related to the film stress. In addition, the fitted β value indicates that the AZO film falls under the ionic class. The photoluminescence spectrum indicates a photoluminescence mechanism of the direct and wide energy gap semiconductor.

ATOMIC AND MOLECULAR PHYSICS

Select

The geometry structures and electronic properties of LimBn (m+n=12) clusters Ruan Wen (阮文), Xie An-Dong (谢安东), Wu Dong-Lan (伍冬兰), Luo Wen-Lang (罗文浪), Yu Xiao-Guang (余晓光) Chin. Phys. B, 2014, 23 (3):  033101.  DOI: 10.1088/1674-1056/23/3/033101 Abstract ( 608 )   PDF (702KB) ( 488 )   The geometric structures, electronic properties, total and binding energies, harmonic frequencies, the highest occupied molecular orbital to the lowest unoccupied molecular orbital energy gaps, and the vertical ionization potential energies of small LimBn (m+n=12) clusters were investigated by the density functional theory B3LYP with a 6-311+G (2d, 2p) basis set. All the calculations were performed using the Gaussian09 program. For the study of the LimBn clusters, the global minimum of the B12 cluster was chosen as the starting point and the boron atoms were gradually replaced by Li atoms. The results showed that as the number of Li atoms increased, the stability of the LimBn cluster decreased and the physical and chemical properties became more active. In addition, on average there was a large charge transfer from the Li atoms to the B atoms.

Select

Diversity of photonic differentiators based on flexible demodulation of phase signals Zheng Ao-Ling (郑傲凌), Dong Jian-Ji (董建绩), Lei Lei (雷蕾), Yang Ting (杨婷), Zhang Xin-Liang (张新亮) Chin. Phys. B, 2014, 23 (3):  033201.  DOI: 10.1088/1674-1056/23/3/033201 Abstract ( 615 )   PDF (417KB) ( 317 )   We theoretically propose a multifunctional photonic differentiation (DIFF) scheme based on phase demodulation using two cascaded linear filters. The photonic DIFF has a diversity of output forms, such as the 1st order intensity DIFF, the 1st order field DIFF and its inversion, and the 2nd-order field DIFF, depending on the relative shift between the optical carrier and the filter’s resonant notches. As a proof, we also experimentally demonstrate the DIFF diversity using a phase modulator and two delay interferometers (DIs). The calculated average deviation is less than 7% for all DIFF waveforms. Our schemes show the advantages of flexible DIFF functions and forms, which may have different optical applications. For example, high order field differentiators can be used to generate complex temporal waveforms, and intensity differentiators are useful for the ultra-wideband pulse generation.

Select

Role of excited states in the elliptically polarized harmonic generation Du Hong-Chuan (杜洪川), Wen Yi-Zhen (文一震), Wang Xiao-Shan (王小山), Hu Bi-Tao (胡碧涛) Chin. Phys. B, 2014, 23 (3):  033202.  DOI: 10.1088/1674-1056/23/3/033202 Abstract ( 665 )   PDF (678KB) ( 401 )   We theoretically investigate the contribution of the excited state to the ellipticity of the harmonics from H2+ at different orientation angles irradiated by a linearly polarized laser pulse. It is found that the first excited state has a significant influence to the ellipticity of the harmonics, and the contribution of higher excited states to the ellipticity can be neglected. Moreover, the conclusion is not dependent on the laser intensity.

Select

The ternary Ni–Al–Co embedded-atom-method potential for γ/γ’ Ni-based single-crystal superalloys：Construction and application Du Jun-Ping (杜俊平), Wang Chong-Yu (王崇愚), Yu Tao (于涛) Chin. Phys. B, 2014, 23 (3):  033401.  DOI: 10.1088/1674-1056/23/3/033401 Abstract ( 740 )   PDF (830KB) ( 556 )   An Ni–Al–Co system embedded-atom-method potential is constructed for the γ(Ni)/γ’(Ni3Al) superalloy based on experiments and first-principles calculations. The stacking fault energies (SFEs) of the Ni(Co, Al) random solid solutions are calculated as a function of the concentrations of Co and Al. The calculated SFEs decrease with increasing concentrations of Co and Al, which is consistent with the experimental results. The embedding energy term in the present potential has an important influence on the SFEs of the random solid solutions. The cross-slip processes of a screw dislocation in homogenous Ni(Co) solid solutions are simulated using the present potential and the nudged elastic band method. The cross-slip activation energies increase with increasing Co concentration, which implies that the creep resistance of γ (Ni) may be improved by the addition of Co.

ELECTROMAGNETISM, OPTICS, ACOUSTICS, HEAT TRANSFER, CLASSICAL MECHANICS, AND FLUID DYNAMICS

Select

Frequency-selective microwave polarization rotator using substrate-integrated waveguide cavities Zuo Yu (左钰), Shen Zhong-Xiang (沈忠祥), Feng Yi-Jun (冯一军) Chin. Phys. B, 2014, 23 (3):  034101.  DOI: 10.1088/1674-1056/23/3/034101 Abstract ( 830 )   PDF (919KB) ( 823 )   A frequency selective polarization rotator that can rotate the polarization angle of an incident electromagnetic wave at the microwave frequency by 45° is presented. The polarization rotator is based on a two-dimensional periodic array of substrate integrated waveguide cavities, realizing the polarization rotation by coupling the input signal to the output wave through three metallic slots. Two layers of frequency selective surfaces are cascaded by substrate and form the polarization rotator. A vertical slot on the top layer is used to select the horizontal polarization from the incident wave, the vertical and the horizontal slots on the bottom layer are, respectively, used to obtain horizontally and vertically polarized outgoing waves. The two orthogonal outgoing waves are combined to result in the 45° polarized wave. Both full wave simulation and experimental measurement are carried out, together validating the proposed method.

Select

Propagation characteristics of power line harmonic radiation in the ionosphere Wu Jing (吴静), Fu Jing-Jing (付静静), Zhang Chong (张翀) Chin. Phys. B, 2014, 23 (3):  034102.  DOI: 10.1088/1674-1056/23/3/034102 Abstract ( 530 )   PDF (306KB) ( 420 )   Theoretical model and solutions on power line harmonic radiation (PLHR) propagating in the ground, air, and anisotropic homogeneous ionosphere are presented. The theoretical model is verified by the PLHR events observed by the DEMETER satellite. Some propagation characteristics of PLHR based on the model are obtained. This paper is beneficial to quantitatively interpret the formation mechanism of PLHR phenomenon.

Select

Effects of self-fields on electron trajectory and gain in planar wiggler free-electron lasers with two-stream and ion-channel guiding S. Saviz, M. Karimi Chin. Phys. B, 2014, 23 (3):  034103.  DOI: 10.1088/1674-1056/23/3/034103 Abstract ( 663 )   PDF (762KB) ( 842 )   The effects of self-fields on electron trajectories and gain in planar wiggler free-electron lasers with two-stream and ion-channel guiding are investigated. An analysis of the two-stream quasi-steady-state electron trajectories is given by solving the equation of motion in the presence of ion-channel guiding and the planar wiggler. The electron trajectories and the gain are derived. The stability of the trajectories, the characteristics of the linear gain, and the normalized maximum gain are studied numerically. The numerical calculations show that there are eight group trajectories rather than the two groups reported in the absence of the self-fields. It is also shown that the normalized gain group seven (G7) decreases while the rest increases with the increase in normalized ion-channel frequency. The two-stream instability and the self-field lead to a decrease in the maximum gain, except for G7.

Select

Numerical simulation for all-optical Thomson scattering X-ray source Tan Fang (谭放), Zhu Bin (朱斌), Han Dan (韩丹), Xin Jian-Ting (辛建婷), Zhao Zong-Qing (赵宗清), Cao Lei-Feng (曹磊峰), Gu Yu-Qiu (谷渝秋), Zhang Bao-Han (张保汉) Chin. Phys. B, 2014, 23 (3):  034104.  DOI: 10.1088/1674-1056/23/3/034104 Abstract ( 543 )   PDF (1156KB) ( 611 )   Energy spectra, angular distributions, and temporal profiles of the photons produced by an all-optical Thomson scattering X-ray source are explored through numerical simulations based on the parameters of the SILEX-I laser system (800 nm, 30 fs, 300 TW) and the previous wakefield acceleration experimental results. The simulation results show that X-ray pulses with a duration of 30 fs and an emission angle of 50 mrad can be produced from such a source. Using the optimized electron parameters, X-ray pulses with better directivity and narrower energy spectra can be obtained. Besides the electron parameters, the laser parameters such as the wavelength, pulse duration, and spot size also affect the X-ray yield, the angular distribution, and the maximum photon energy, except the X-ray pulse duration which is slightly changed for the case of ultrafast laser–electron interaction.

Select

Temperature dependence of the refractive index of optical fibers Wang Zhi-Yong (王智勇), Qiu Qi (邱琪), Shi Shuang-Jin (史双瑾) Chin. Phys. B, 2014, 23 (3):  034201.  DOI: 10.1088/1674-1056/23/3/034201 Abstract ( 1028 )   PDF (208KB) ( 2255 )   Many experimental investigations on the temperature dependence of the refractive index of optical fibers have been reported previously, however a satisfying theoretical explanation for it is still absent. In this paper, a theoretical model about the temperature dependence of the refractive index of optical fibers is presented and it is in agreement with the previous experimental results. This work is a significant reference for the research and development of temperature sensors based on optical fiber delay lines.

Select

Transmission through array of subwavelength metallic slits curved with a single step or multi-step Wang Ying-Qi (王瑛琪), Wang Yan-Hua (王艳花), Zheng Xian-Hua (郑显华), Ye Jia-Sheng (叶佳声), Zhang Yan (张岩), Liu Shu-Tian (刘树田) Chin. Phys. B, 2014, 23 (3):  034202.  DOI: 10.1088/1674-1056/23/3/034202 Abstract ( 644 )   PDF (1062KB) ( 466 )   The transmission of normally incident plane wave through an array of subwavelength metallic slits curved with a single step or mutli-step has been explored theoretically. The transmission spectrum is simulated by using the finite-difference time-domain method. The influences of surface plasmon polaritons make the end of finite long sub-wavelength metallic slit behaves as magnetic-reflecting barrier. The electromagnetic fields in the subwavelength metallic slits are the superposition of standing wave and traveling wave. The standing electromagnetic oscillation behaves like LC oscillating circuit to decide the resonance wavelength. Therefore, the parameters of adding step may change the LC circuit and influence the transmission wavelength. A new explanation model is proposed in which the resonant wavelength is decided by four factors: the changed length for electric field, the changed length for magnetic field, the effective coefficient of capacitance, and the effective coefficient of inductance. The effect of adding step is presented to analyze the interaction of two steps in slit with mutli-step. This explanation model has been proved by the transmission through arrayed subwavelength metallic slits curved with two steps and fractal steps. All calculated results are well explained by our proposed model.

Select

Entanglement of two two-level atoms trapped in coupled cavities with a Kerr medium Wu Qin (吴琴), Zhang Zhi-Ming (张智明) Chin. Phys. B, 2014, 23 (3):  034203.  DOI: 10.1088/1674-1056/23/3/034203 Abstract ( 579 )   PDF (753KB) ( 399 )   In this paper, the entanglement dynamics of two two-level atoms trapped in coupled cavities with a Kerr medium is investigated. We find that the phenomena of entanglement sudden death (ESD) and entanglement sudden birth (ESB) appear during the evolution process. The influences of initial atomic states, Kerr medium, and cavity–cavity hopping rate on the atom–atom entanglement are discussed. The results obtained by the numerical method show that the atom–atom entanglement is strengthened and even prevented from ESD with increasing cavity–cavity hopping rate and Kerr nonlinearity.

Select

Dynamics of quantum discord in a two-qubit system under classical noise Guo You-Neng (郭有能), Fang Mao-Fa (方卯发), Liu Xiang (刘翔), Yang Bai-Yuan (杨百元) Chin. Phys. B, 2014, 23 (3):  034204.  DOI: 10.1088/1674-1056/23/3/034204 Abstract ( 634 )   PDF (654KB) ( 831 )   We study the quantum discord dynamics of two noninteracting qubits that are, respectively, subject to classical noise. The results show that the dynamics of quantum discord are dependent on both the coupling between the qubits and classical noise, and the average switching rate of the classical noise. In the weak-coupling Markovian region, quantum discord exhibits exponent decay without revival, and can be well protected by increasing the average classical noise switching rate. While in the strong-coupling non-Markovian region, quantum discord reveals slowly decayed oscillations with quick revival by decreasing the average switching rate of the classical noise. Thus, our results provide a new method of protecting quantum discord in a two-qubit system by controlling the coupling between the qubits and classical noise, and the average switching rate of the classical noise.

Select

Multi-ion Mach–Zehnder interferometer with artificial nonlinear interactions Hu Yan-Min (胡艳敏), Yang Wan-Li (杨万里), Xiao Xing (肖兴), Feng Mang (冯芒), Li Chao-Hong (李朝红) Chin. Phys. B, 2014, 23 (3):  034205.  DOI: 10.1088/1674-1056/23/3/034205 Abstract ( 894 )   PDF (306KB) ( 404 )   We propose a method to implement a Mach–Zehnder interferometry based upon a string of trapped ions with artificial nonlinear interactions. By manipulating the coupling strength between two involved internal states of the ions, we could achieve the beam splitting/recombination with NOON states. Using current techniques for manipulating trapped ions, we discuss the experimental feasibility of our scheme and analyze some undesired uncertainty under realistic experimental environment.

Select

Highly sensitive digital optical sensor with large measurement range based on the dual-microring resonator with waveguide-coupled feedback Xiang Xing-Ye (向星烨), Wang Kui-Ru (王葵如), Yuan Jin-Hui (苑金辉), Jin Bo-Yuan (晋博源), Sang Xin-Zhu (桑新柱), Yu Chong-Xiu (余重秀) Chin. Phys. B, 2014, 23 (3):  034206.  DOI: 10.1088/1674-1056/23/3/034206 Abstract ( 578 )   PDF (321KB) ( 522 )   We propose a novel high-performance digital optical sensor based on the Mach–Zehnder interferential effect and the dual-microring resonators with the waveguide-coupled feedback. The simulation results show that the sensitivity of the sensor can be orders of magnitude higher than that of a conventional sensor, and high quality factor is not critical in it. Moreover, by optimizing the length of the feedback waveguide to be equal to the perimeter of the ring, the measurement range of the proposed sensor is twice as much as that of the conventional sensor in the weak coupling case.

Select

A narrow-linewidth continuous wave Ho：YALO3 laser with Fabry–Perot etalons Yang Xiao-Tao (杨晓涛) Chin. Phys. B, 2014, 23 (3):  034207.  DOI: 10.1088/1674-1056/23/3/034207 Abstract ( 620 )   PDF (236KB) ( 421 )   A narrow linewidth continuous wave Ho:YAP laser with two Fabry–Perot etalons pumped by a Tm:YLF laser is reported. The maximum output power reaches 8.3 W when the incident pump power is 15.8 W, with 52.5% optical-to-optical conversion efficiency and 62.6% slope efficiency. A stable laser output at 2118.1 nm is achieved, with a linewidth less than 0.4 nm (full width at half maximum). The beam quality factor is M2～1.25, measured by the traveling knife-edge method.

Select

UV–visible spectral characterization and density functional theory simulation analysis on laser-induced crystallization of amorphous silicon thin films Huang Lu (黄璐), Jin Jing (金晶), Shi Wei-Min (史伟民), Yuan Zhi-Jun (袁志军), Yang Wei-Guang (杨伟光), Cao Ze-Chun (曹泽淳), Wang Lin-Jun (王林军), Zhou Jun (周军), Lou Qi-Hong (楼祺洪) Chin. Phys. B, 2014, 23 (3):  034208.  DOI: 10.1088/1674-1056/23/3/034208 Abstract ( 643 )   PDF (624KB) ( 423 )   The effect of laser energy density on the crystallization of hydrogenated intrinsic amorphous silicon (a-Si:H) thin films was studied both theoretically and experimentally. The thin films were irritated by a frequency-doubled (λ=532 nm) Nd:YAG pulsed nanosecond laser. An effective density functional theory model was built to reveal the variation of bandgap energy influenced by thermal stress after laser irradiation. Experimental results establish correlation between the thermal stress and the shift of transverse optical peak in Raman spectroscopy and suggest that the relatively greater shift of the transverse optical (TO) peak can produce higher stress. The highest crystalline fraction (84.5%) is obtained in the optimized laser energy density (1000 mJ/cm2) with a considerable stress release. The absorption edge energy measured by the UV-visible spectra is in fairly good agreement with the bandgap energy in the density functional theory (DFT) simulation.

Select

Intensity and composition-dependent sign reversal of non-linearity in TiO2/CeO2 nanocomposites S. Divya, V. P. N. Nampoori, P. Radhakrishnan, A. Mujeeb Chin. Phys. B, 2014, 23 (3):  034209.  DOI: 10.1088/1674-1056/23/3/034209 Abstract ( 599 )   PDF (521KB) ( 669 )   CeO2/TiO2 composite nanoparticles with different Ce/Ti molar ratios have been successfully synthesized via sol–gel method. It was found that the band gap of the nanocomposite is tunable by varying Ce/Ti content. The nonlinear response of the sample was studied by using the nanosecond laser pulses from a Q switched Nd:Yag laser employing the Z-scan method. Open aperture Z-scan experiment revealed that with the increase in the CeO2 amount in the nanocomposite, the non-linearity of the composite increases, and it was assumed that this could be due to the modification of TiO2 dipole symmetry by the addition of CeO2. Closed aperture Z-scan experiment showed that when the CeO2 amount increases, positive nonlinear refraction decreases, and this could be attributed to the increase in the two photon absorption which subsequently suppresses the nonlinear refraction.

Select

Tailoring optical properties of TiO2 in silica glass for limiting applications S. Divya, Indu Sebastian, V. P. N. Nampoori, P. Radhakrishnan, A. Mujeeb Chin. Phys. B, 2014, 23 (3):  034210.  DOI: 10.1088/1674-1056/23/3/034210 Abstract ( 643 )   PDF (479KB) ( 533 )   We present the linear and nonlinear optical studies on TiO2–SiO2 nanocomposites with varying compositions. Optical band gap of the material is found to vary with the amount of SiO2 in the composite. The phenomenon of two-photon absorption (TPA) in TiO2/SiO2 nanocomposites has been studied using open aperture Z-scan technique. The nanocomposites show better nonlinear optical properties than pure TiO2, which can be attributed to the surface states and weak dielectric confinement of TiO2 nanoparticles by SiO2 matrix. The nanocomposites are thermally treated and similar studies are performed. The anatase form of TiO2 in the nanocomposites shows superior properties relative to the amorphous and rutile counterpart. The involved mechanism is explained by rendering the dominant role played by the excitons in the TiO2 nanoparticles.

Select

Optical properties of the electromagnetic waves propagating in an elliptical cylinder multilayer structure A. Abdoli-Arani Chin. Phys. B, 2014, 23 (3):  034211.  DOI: 10.1088/1674-1056/23/3/034211 Abstract ( 873 )   PDF (239KB) ( 571 )   Theoretical description of the wave propagation in an elliptical cylinder multilayer structure under the conditions of H polarization and E polarization is presented. A transfer matrix method has been developed for elliptical cylinder waves. The formulas of reflection and transmission coefficients for an elliptical cylinder multilayer structure are driven. Reflection and transmission coefficients of elliptical cylinder waves by a single elliptical cylinder interface is presented. The obtained formulas can be generalized to the cold plasma filled structures and thus the obtained results in the limit of circular cylinder structures are investigated.

Select

Effect of optical pump on the dielectric properties of SrTiO3 in terahertz range Wu Liang (吴亮), Jiang Lin-Kun (蒋霖坤), Yuan Cai (袁偲), Ding Xin (丁欣), Yao Jian-Quan (姚建铨) Chin. Phys. B, 2014, 23 (3):  034212.  DOI: 10.1088/1674-1056/23/3/034212 Abstract ( 586 )   PDF (329KB) ( 824 )   Tuning the dielectric permittivity spectra of strontium titanate (SrTiO3) single crystals in an external optical field is investigated at room temperature by means of terahertz time-domain spectroscopy. The application of the optical field leads to an appreciable tuning of the permittivity, reaching up to 2.8%, with the dielectric loss changing about 3%. The observed behavior is interpreted in terms of soft-mode hardening due to the anharmonic character of its potential. We also find that the change of the refractive index responds linearly to the applied light power. These findings are attributed to a linear electro-optical effect of the internal space charge field of the crystal.

Select

Subwavelength beam manipulation via multiple-metal slits coupled by disk-shaped nanocavity Zheng Gai-Ge (郑改革), Xu Lin-Hua (徐林华), Pei Shi-Xin (裴世鑫), Chen Yun-Yun (陈云云) Chin. Phys. B, 2014, 23 (3):  034213.  DOI: 10.1088/1674-1056/23/3/034213 Abstract ( 542 )   PDF (483KB) ( 497 )   A novel plasmonic structure consisting of three nano-scaled slits coupled by nano-disk-shaped nanocavities is proposed to produce subwavelength focusing and beam bending at optical frequencies. The incident light passes through the metal slits in the form of surface plasmon polaritons (SPPs) and then scatters into radiation fields. Numerical simulations using finite-difference time-domain (FDTD) method show that the transmitted fields through the design example can generate light focusing and deflection by altering the refractive index of the coupled nanocavity. The simulation results indicate that the focal spot is beyond the diffraction limit. Light impinges on the surface at an angle to the optical axis will add an extra planar phase front that interferes with the asymmetric phase front of the plasmonic lens, leading to a larger bending angle off the axial direction. The advantages of the proposed plasmonic lens are smaller device size and ease of fabrication. Such geometries offer the potential to be controlled by using nano-positioning systems for applications in dynamic beam shaping and scanning on the nanoscale.

Select

Spatiotemporal binary interaction and designer quasi-particle condensates Ramaswamy Radha, Pattu Sakthi Vinayagam, Hyun Jong Shin, Kuppuswamy Porsezian Chin. Phys. B, 2014, 23 (3):  034214.  DOI: 10.1088/1674-1056/23/3/034214 Abstract ( 637 )   PDF (2362KB) ( 342 )   We introduce a new integrable model to investigate the dynamics of two component quasi-particle condensates with spatiotemporal interaction strengths. We derive the associated Lax pair of the coupled Gross–Pitaevskii (GP) equation and construct matter wave solitons. We show that the spatiotemporal binary interaction strengths not only facilitate the stabilization of the condensates, but also enables one to fabricate condensates with desirable densities, geometries, and properties, leading to the so-called “designer quasi-particle condensates”.

Select

Asymmetric light propagation based on semi-circular photonic crystals Wang Lin-Hui (王林辉), Yang Xiu-Lun (杨修伦), Meng Xiang-Feng (孟祥锋), Wang Yu-Rong (王玉荣), Chen Shou-Xiang (陈寿翔), Huang Zhe (黄哲), Dong Guo-Yan (董国艳) Chin. Phys. B, 2014, 23 (3):  034215.  DOI: 10.1088/1674-1056/23/3/034215 Abstract ( 544 )   PDF (1389KB) ( 465 )   A new structure based on a semi-circular photonic crystal is proposed to achieve asymmetric light propagation. The semi-circular photonic crystal structure proposed in this paper is a deformation of a two-dimensional conventional square photonic crystal. Through the directional bandgap of the semi-circular photonic crystal, the light from one direction can transfer to the other side, but the light from the opposite direction cannot. A high contrast ratio is obtained by designing the constitutive parameters of the photonic crystal and choosing the suitable light frequency. This structure promises a significant potential in optical integration and other areas.

Select

A three-dimensional Eulerian method for the numerical simulation of high-velocity impact problems Wu Shi-Yu (吴士玉), Liu Kai-Xin (刘凯欣), Chen Qian-Yi (陈千一) Chin. Phys. B, 2014, 23 (3):  034601.  DOI: 10.1088/1674-1056/23/3/034601 Abstract ( 549 )   PDF (1057KB) ( 362 )   In the present paper, a three-dimensional (3D) Eulerian technique for the 3D numerical simulation of high-velocity impact problems is proposed. In the Eulerian framework, a complete 3D conservation element and solution element scheme for conservative hyperbolic governing equations with source terms is given. A modified ghost fluid method is proposed for the treatment of the boundary conditions. Numerical simulations of the Taylor bar problem and the ricochet phenomenon of a sphere impacting a plate target at an angle of 60° are carried out. The numerical results are in good agreement with the corresponding experimental observations. It is proved that our computational technique is feasible for analyzing 3D high-velocity impact problems.

Select

Large-eddy simulations of a forced homogeneous isotropic turbulence with polymer additives Wang Lu (王璐), Cai Wei-Hua (蔡伟华), Li Feng-Chen (李凤臣) Chin. Phys. B, 2014, 23 (3):  034701.  DOI: 10.1088/1674-1056/23/3/034701 Abstract ( 545 )   PDF (2967KB) ( 408 )   Large-eddy simulations (LES) based on the temporal approximate deconvolution model were performed for a forced homogeneous isotropic turbulence (FHIT) with polymer additives at moderate Taylor Reynolds number. Finitely extensible nonlinear elastic in the Peterlin approximation model was adopted as the constitutive equation for the filtered conformation tensor of the polymer molecules. The LES results were verified through comparisons with the direct numerical simulation results. Using the LES database of the FHIT in the Newtonian fluid and the polymer solution flows, the polymer effects on some important parameters such as strain, vorticity, drag reduction, and so forth were studied. By extracting the vortex structures and exploring the flatness factor through a high-order correlation function of velocity derivative and wavelet analysis, it can be found that the small-scale vortex structures and small-scale intermittency in the FHIT are all inhibited due to the existence of the polymers. The extended self-similarity scaling law in the polymer solution flow shows no apparent difference from that in the Newtonian fluid flow at the currently simulated ranges of Reynolds and Weissenberg numbers.

Select

Attractor comparison analysis for characterizing vertical upward oil–gas–water three-phase flow Zhao Jun-Ying (赵俊英), Jin Ning-De (金宁德), Gao Zhong-Ke (高忠科), Du Meng (杜萌), Wang Zhen-Ya (王振亚) Chin. Phys. B, 2014, 23 (3):  034702.  DOI: 10.1088/1674-1056/23/3/034702 Abstract ( 547 )   PDF (1004KB) ( 441 )   We investigate the dynamic characteristics of oil–gas–water three-phase flow in terms of chaotic attractor comparison. In particular, we extract a statistic to characterize the dynamical difference in attractor probability distribution. We first take time series from Logistic chaotic system with different parameters as examples to demonstrate the effectiveness of the method. Then we use this method to investigate the experimental signals from oil–gas–water three-phase flow. The results indicate that the extracted statistic is very sensitive to the change of flow parameters and can gain a quantitatively insight into the dynamic characteristics of different flow patterns.

Select

Three-dimensional numerical simulation of crown spike due to coupling effect between bubbles and free surface Han Rui (韩蕊), Zhang A-Man (张阿漫), Li Shuai (李帅) Chin. Phys. B, 2014, 23 (3):  034703.  DOI: 10.1088/1674-1056/23/3/034703 Abstract ( 629 )   PDF (2256KB) ( 358 )   The motion of gas bubbles beneath a free surface will lead to a spike of fluid on the free surface. The distance of the bubbles to the free surface is the key factor to different phenomena. When the inception distance varies in some range, crown phenomenon would happen after the impact of weak buoyancy bubbles, so this kind of spike is defined as crown spike in the present paper. Based on potential flow theory, a three-dimensional numerical model is established to simulate the motion of the free-surface spike generated by one bubble or a horizontal line of two in-phase bubbles. After the downward jet formed near the end of the collapse phase, the simulation of the free surface is performed to study the crown spike without regard to the toroidal bubble’s effect. Calculations about the interaction between one bubble and free surface agree well with the experimental results conducted with a high-speed camera, and relative error is within 15%. Crown spike in both single-and two-bubble cases are simulated numerically. Different features and laws of the motion of crown spike, depending on the bubble-boundary distances and the inter-bubble distances, have been investigated.

Select

Flow characterization and dilution effects of N2 and CO2 on premixed CH4/air flames in a swirl-stabilized combustor Han Yue (韩乐), Cai Guo-Biao (蔡国飙), Wang Hai-Xing (王海兴), Renou Bruno, Boukhalfa Abdelkrim Chin. Phys. B, 2014, 23 (3):  034704.  DOI: 10.1088/1674-1056/23/3/034704 Abstract ( 492 )   PDF (2679KB) ( 538 )   Numerically-aided experimental studies are conducted on a swirl-stabilized combustor to investigate the dilution effects on flame stability, flame structure, and pollutant emissions of premixed CH4/air flames. Our goal is to provide a systematic assessment on combustion characteristics in diluted regimes for its application to environmentally-friendly approaches such as biogas combustion and exhaust-gas recirculation technology. Two main diluting species, N2 and CO2, are tested at various dilution rates. The results obtained by means of optical diagnostics show that five main flame regimes can be observed for N2-diluted flames by changing excess air and dilution rate. CO2-diluted flames follow the same pattern evolution except that all the domains are shifted to lower excess air. Both N2 and CO2 dilution affect the lean blow-out (LBO) limits negatively. This behavior can be counter-balanced by reactant preheating which is able to broaden the flammability domain of the diluted flames. Flame reactivity is degraded by increasing dilution rate. Meanwhile, flames are thickened in the presence of both diluting species. NOx emissions are significantly reduced with dilution and proved to be relevant to flame stability diagrams: slight augmentation in NOx emission profiles is related to transitional flame states where instability occurs. Although dilution results in increase in CO emissions at certain levels, optimal dilution rates can still be proposed to achieve an ideal compromise.

PHYSICS OF GASES, PLASMAS, AND ELECTRIC DISCHARGES

Select

Investigation on the shockwave induced by surface arc plasma in quiescent air Jin Di (金迪), Li Ying-Hong (李应红), Jia Min (贾敏), Li Fan-Yu (李凡玉), Cui Wei (崔巍), Sun Quan (孙权), Zhang Bai-Ling (张百灵), Li Jun (李军) Chin. Phys. B, 2014, 23 (3):  035201.  DOI: 10.1088/1674-1056/23/3/035201 Abstract ( 640 )   PDF (1113KB) ( 531 )   The shockwave induced by surface direct-current (DC) arc discharge is investigated both experimentally and numerically. In the experiment, the shockwave generated by rapid gas heating is clearly observed from Schlieren images. The peak velocity of the shockwave is measured to be over 410 m/s; during its upright movement, it gradually falls to about 340 m/s; no remarkable difference is seen after changing the discharge voltage and the pulse frequency. In the modeling of the arc plasma, the arc domain is not simulated as a boundary condition with fixed temperature or pressure, but a source term with a time-varying input power density, which could better reflect the influence of the heating process. It is found that with a reference power density of 2.8×1012 W/m3, the calculated peak velocity is higher than the measured one, but they quickly (in 30 μs) become agreed with each other. The peak velocity also rises while increasing the power density, the maximum velocity acquired in the simulation is over 468 m/s, which is expected to be effective for high speed flow control.

Select

Electromagnetic interaction between local surface plasmon polaritons and an atmospheric surface wave plasma jet Chen Zhao-Quan (陈兆权), Hu Dong (胡东), Liu Ming-Hai (刘明海), Xia Guang-Qing (夏广庆), Zheng Xiao-Liang (郑晓亮), Hu Ye-Lin (胡业林), Ye Qiu-Bo (叶秋波), Chen Ming-Gong (陈明功), Zhu Long-Ji (祝龙记), Hu Xi-Wei (胡希伟) Chin. Phys. B, 2014, 23 (3):  035202.  DOI: 10.1088/1674-1056/23/3/035202 Abstract ( 645 )   PDF (748KB) ( 662 )   We analyze the electromagnetic interaction between local surface plasmon polaritons (SPPs) and an atmospheric surface wave plasma jet (ASWPJ) in combination with our designed discharge device. Before discharge, the excitation of the SPPs and the spatial distribution of the enhanced electric field are analyzed. During discharge, the critical breakdown electric field of the gases at atmospheric gas pressure and the surface wave of the SPPs converted into electron plasma waves at resonant points are studied. After discharge, the ionization development process of the ASWPJ is simulated using a two-dimensional fluid model. Our results suggest that the local enhanced electric field of SPPs is merely the precondition of gas breakdown, and the key mechanism in maintaining the discharge development of a low-power ASWPJ is the wave-mode conversion of the local enhanced electric field at the resonant point.

Select

Growth of small diameter multi-walled carbon nanotubes by arc discharge process K. T. Chaudhary, J. Ali, P. P. Yupapin Chin. Phys. B, 2014, 23 (3):  035203.  DOI: 10.1088/1674-1056/23/3/035203 Abstract ( 642 )   PDF (1541KB) ( 474 )   Multi-walled carbon nanotubes (MWCNTs) are grown by arc discharge method in a controlled methane environment. The arc discharge is produced between two graphite electrodes at the ambient pressures of 100 torr, 300 torr, and 500 torr. Arc plasma parameters such as temperature and density are estimated to investigate the influences of the ambient pressure and the contributions of the ambient pressure to the growth and the structure of the nanotubes. The plasma temperature and density are observed to increase with the increase in the methane ambient pressure. The samples of MWCNT synthesized at different ambient pressures are analyzed using transmission electron microscopy, scanning electron microscopy, Raman spectroscopy, Fourier transform infrared spectroscopy, and X-ray diffraction. An increase in the growth of MWCNT and a decrease in the inner tube diameter are observed with the increase in the methane ambient pressure.

Select

On the energy conservation electrostatic particle-in-cell/Monte Carlo simulation：Benchmark and application to the radio frequency discharges Wang Hong-Yu (王虹宇), Jiang Wei (姜巍), Sun Peng (孙鹏), Kong Ling-Bao (孔令宝) Chin. Phys. B, 2014, 23 (3):  035204.  DOI: 10.1088/1674-1056/23/3/035204 Abstract ( 846 )   PDF (546KB) ( 651 )   We benchmark and analyze the error of energy conservation (EC) scheme in particle-in-cell/Monte Carlo (PIC/MC) algorithms by simulating the radio frequency discharge. The plasma heating behaviors and electron distributing functions obtained by one-dimensional (1D) simulation are analyzed. Both explicit and implicit algorithms are checked. The results showed that the EC scheme can eliminated the self-heating with wide grid spacing in both cases with a small reduction of the accuracies. In typical parameters, the EC implicit scheme has higher precision than EC explicit scheme. Some “numerical cooling” behaviors are observed and analyzed. Some other errors are also analyzed. The analysis showed that the EC implicit scheme can be used to qualitative estimation of some discharge problems with much less computational resource cost without much loss of accuracies.

Select

Preparation of biomedical Ag incorporated hydroxyapatite/titania coatings on Ti6Al4V alloy by plasma electrolytic oxidation Zhou Lan (周澜), Lü Guo-Hua (吕国华), Mao Fei-Fei (毛菲菲), Yang Si-Ze (杨思泽) Chin. Phys. B, 2014, 23 (3):  035205.  DOI: 10.1088/1674-1056/23/3/035205 Abstract ( 605 )   PDF (957KB) ( 485 )   Nano-Ag incorporated hydroxyapatite/titania (HA/TiO2) coatings were deposited on Ti6Al4V substrates by the plasma electrolytic oxidation process. Compared with the substrate, the deposited coatings display attractive mechanical and biomedical properties. First, the coatings have stronger wear resistance and corrosion resistance. Second, they show a strong antibacterial ability. The mean vitality of the P. gingivalis on the coating surfaces is reduced to about 21%. Third, the coatings have good biocompatibility. The mean viability of the fibroblast cells on the coating surface is increased to about 130%. With these attractive properties, Ag incorporated HA/TiO2 coatings may be useful in the biomedical field.

CONDENSED MATTER: STRUCTURAL, MECHANICAL, AND THERMAL PROPERTIES

Select

Mechanical properties of self-irradiated single-crystal copper Li Wei-Na (李维娜), Xue Jian-Ming (薛建明), Wang Jian-Xiang (王建祥), Duan Hui-Ling (段慧玲) Chin. Phys. B, 2014, 23 (3):  036101.  DOI: 10.1088/1674-1056/23/3/036101 Abstract ( 694 )   PDF (1759KB) ( 1286 )   Molecular dynamics simulations are performed to investigate the influence of irradiation damage on the mechanical properties of copper. In the simulation, the energy of primary knocked-on atoms (PKAs) ranges from 1 to 10 keV, and the results indicate that the number of point defects (vacancies and interstitials) increases linearly with the PKA energy. We choose three kinds of simulation samples: un-irradiated and irradiated samples, and comparison samples. The un-irradiated samples are defect-free, while irradiation induces vacancies and interstitials in the irradiated samples. It is found that due to the presence of the irradiation-induced defects, the compressive Young modulus of the single-crystal Cu increases, while the tensile Young modulus decreases, and that both the tensile and compressive yield stresses experience a dramatic decrease. To analyze the effects of vacancies and interstitials independently, the mechanical properties of the comparison samples, which only contain randomly distributed vacancies, are investigated. The results indicate that the vacancies are responsible for the change of Young modulus, while the interstitials determine the yield strain.

Select

Microstructure evolution of zircaloy-4 during Ne ion irradiation and annealing：An in situ TEM investigation Shen Hua-Hai (申华海), Peng Shu-Ming (彭述明), Zhou Xiao-Song (周晓松), Sun Kai (孙凯), Wang Lu-Ming (王鲁闽), Zu Xiao-Tao (祖小涛) Chin. Phys. B, 2014, 23 (3):  036102.  DOI: 10.1088/1674-1056/23/3/036102 Abstract ( 635 )   PDF (449KB) ( 473 )   The microstructural evolution of zircaloy-4 was studied, including the amorphization and recrystallization of Zr(Fe, Cr)2 precipitates, and the density of dislocations under in situ Ne ion irradiation and post annealing. The results show that irradiation at a relatively high temperature and dose induces the formation of nanocrystals in pre-amorphized Zr(Fe, Cr)2 precipitates. The recrystallized nanocrystals also have the structure of hcp-Zr(Fe, Cr)2. The formation of the nanocrystals is thought to be the consequence of competition between atomistic disordering and the recrystallization of precipitates under ion irradiation. The free energy of the nanocrystal is lower than that of the amorphous state, which is another reason for the recrystallization of the precipitates. With increased annealing temperature, the density of the nanocrystals is increased. The dislocation density sharply decreases with the increase in the annealing temperature, and its size increases.

Select

Phase separation in Sr doped BiMnO3 Li Guan-Nan (李冠男), Rao Guang-Hui (饶光辉), Huang Qing-Zhen (黄清镇), Gao Qing-Qing (高庆庆), Luo Jun (骆军), Liu Guang-Yao (刘广耀), Li Jing-Bo (李静波), Liang Jing-Kui (梁敬魁) Chin. Phys. B, 2014, 23 (3):  036401.  DOI: 10.1088/1674-1056/23/3/036401 Abstract ( 534 )   PDF (718KB) ( 525 )   Phase separation in Sr doped BiMnO3 (Bi1-xSrxMnO3, x=0.4–0.6) was studied by means of temperature-dependent high-resolution neutron powder diffraction (NPD), high resolution X-ray powder diffraction (XRD), and physical property measurements. All the experiments indicate that a phase separation occurs at the temperature coinciding with the reported charge ordering temperature (TCO) in the literature. Below the reported TCO, both the phases resulting from the phase separation crystallize in the orthorhombically distorted perovskite structure with space group Imma. At lower temperature, these two phases order in the CE-type antiferromagnetic structure and the A-type antiferromagnetic structure, respectively. However, a scrutiny of the high-resolution NPD and XRD data at different temperatures and the electron diffraction experiment at 300 K did not manifest any evidence of a long-range charge ordering (CO) in our investigated samples, suggesting that the anomalies of physical properties such as magnetization, electric transport, and lattice parameters at the TCO might be caused by the phase separation rather than by a CO transition.

Select

Structural and physical properties of BiFeO3 thin films epitaxially grown on SrTiO3 (001) and polar (111) surfaces He Shu-Min (贺树敏), Liu Guo-Lei (刘国磊), Zhu Da-Peng (朱大鹏), Kang Shi-Shou (康仕寿), Chen Yan-Xue (陈延学), Yan Shi-Shen (颜世申), Mei Liang-Mo (梅良模) Chin. Phys. B, 2014, 23 (3):  036801.  DOI: 10.1088/1674-1056/23/3/036801 Abstract ( 513 )   PDF (2569KB) ( 477 )   The influence of surface polarity on the structural properties of BiFeO3 (BFO) thin films is investigated. BFO thin films are epitaxially grown on SrTiO3 (STO) (100) and polar (111) surfaces by oxygen plasma-assisted molecular beam epitaxy. It is shown that the crystal structure, surface morphology, and defect states of BFO films grown on STO substrates with nonpolar (001) or polar (111) surfaces perform very differently. BFO/STO (001) is a fully strained tetragonal phase with orientation relationship (001)[100]BFO‖(001)[100]STO, while BFO/STO (111) is a rhombohedral phase. BFO/STO (111) has rougher surface morphology and less defect states, which results in reduced leakage current and lower dielectric loss. Moreover, BFO films on both STO (001) and STO (111) are direct band oxides with similar band gaps of 2.65 eV and 2.67 eV, respectively.

TOPICAL REVIEW—Magnetism, magnetic materials, and interdisciplinary research

Select

Writability issues in high-anisotropy perpendicular magnetic recording media Wang Fang (王芳), Xu Xiao-Hong (许小红) Chin. Phys. B, 2014, 23 (3):  036802.  DOI: 10.1088/1674-1056/23/3/036802 Abstract ( 523 )   PDF (2222KB) ( 1840 )   Challenges and recent developments associated with writability issues in high-anisotropy perpendicular recording media are reviewed. The writing field is limited by the high coercivity caused by the high anisotropy. Some new alternatives are proposed to solve the writability issues, including texture-tilting-assisted, domain-wall-assisted, energy-assisted magnetic recording technologies, and so on. In addition, we propose new alternatives for the next-generation of magnetic recording media.

RAPID COMMUNICATION

Select

Disappearance of the Dirac cone in silicene due to the presence of an electric field Hot! D. A. Rowlands, Zhang Yu-Zhong (张宇钟) Chin. Phys. B, 2014, 23 (3):  037101.  DOI: 10.1088/1674-1056/23/3/037101 Abstract ( 633 )   PDF (2496KB) ( 436 )   Using the two-dimensional ionic Hubbard model as a simple basis for describing the electronic structure of silicene in the presence of an electric field induced by the substrate, we use the coherent-potential approximation to calculate the zero-temperature phase diagram and the associated spectral function at half filling. We find that any degree of symmetry-breaking induced by the electric field causes the silicene structure to lose its Dirac fermion characteristics, thus providing a simple mechanism for the disappearance of the Dirac cone.

CONDENSED MATTER: ELECTRONIC STRUCTURE, ELECTRICAL, MAGNETIC, AND OPTICAL PROPERTIES

Select

Effect of Cr, Mo, and Nb additions on intergranular cohesion of ferritic stainless steel：First-principles determination Li Chun-Xia (李春霞), Dang Sui-Hu (党随虎), Wang Li-Ping (王丽萍), Zhang Cai-Li (张彩丽), Han Pei-De (韩培德) Chin. Phys. B, 2014, 23 (3):  037102.  DOI: 10.1088/1674-1056/23/3/037102 Abstract ( 662 )   PDF (1778KB) ( 542 )   Effects of Cr, Mo, and Nb on the ferritic stainless steel ∑(210) grain boundary and intragranularity are investigated using the first-principles principle. Different positions of solute atoms are considered. Structural stability is lowered by Cr doping and enhanced by Mo and Nb doping. A ranking on the effect of solute atoms enhancing the cohesive strength of the grain boundary, from the strongest to the weakest is Cr, Mo, and Nb. Cr clearly prefers to locate in the intragranular region of Fe rather than in the grain boundary, while Mo and Nb tend to segregate to the grain boundary. Solute Mo and Nb atoms possess a strong driving force for segregation to the grain boundary from the intragranular region, which increases the grain boundary embrittlement. For Mo-and Nb-doped systems, a remarkable quantity of electrons accumulate in the region close to Mo (Nb). Therefore, the bond strength may increase. With Cr, Mo, and Nb additions, an anti-parallel island is formed around the center of the grain boundary.

Select

Electronic structures and thermoelectric properties of solid solutions CuGa1-xInxTe2：A first-principles study Xue Li (薛丽), Xu Bin (徐斌), Yi Lin (易林) Chin. Phys. B, 2014, 23 (3):  037103.  DOI: 10.1088/1674-1056/23/3/037103 Abstract ( 522 )   PDF (457KB) ( 526 )   The electronic structures of solid solutions CuGa1-xInxTe2 are systematically investigated using the full-potential all-electron linearized augmented plane wave method. The calculated lattice parameters almost linearly increase with the increase of the In composition, which are in good agreement with the available experimental results. The calculated band structures with the modified Becke–Johnson potential show that all solid solutions are direct gap conductors. The band gap decreases linearly with In composition increasing. Based on the electronic structure calculated, we investigate the thermoelectric properties by the semi-classical Boltzmann transport theory. The results suggest that when Ga is replaced by In, the bipolar effect of Seebeck coefficient S becomes very obvious. The Seebeck coefficient even changes its sign from positive to negative for p-type doping at low carrier concentrations. The optimal p-type doping concentrations have been estimated based on the predicted maximum values of the power factor divided by the scattering time.

Select

First-principles study of the electronic structure and optical properties of cubic Perovskite NaMgF3 Li Zhen-Li (李贞丽), An Xin-You (安辛友), Cheng Xin-Lu (程新路), Wang Xue-Min (王雪敏), Zhang Hong (张红), Peng Li-Ping (彭丽萍), Wu Wei-Dong (吴卫东) Chin. Phys. B, 2014, 23 (3):  037104.  DOI: 10.1088/1674-1056/23/3/037104 Abstract ( 589 )   PDF (481KB) ( 1269 )   The structural, electronic, and optical properties of cubic perovskite NaMgF3 are calculated by plane-wave pseudopotential density functional theory. The calculated lattice constant a0, bulk modulus B0, and the derivative of bulk modulus B0’ are 3.872 Å, 78.2 GPa, and 3.97, respectively. The results are in good agreement with the available experimental and theoretical values. The electronic structure shows that cubic NaMgF3 is an indirect insulator with a wide forbidden band gap of Eg=5.90 eV. The contribution of the different bands is analyzed by total and partial density of states curves. Population analysis of NaMgF3 indicates that there is strong ionic bonding in the MgF2 unit, and a mixture of ionic and weak covalent bonding in the NaF unit. Calculations of dielectric function, absorption coefficient, refractive index, electronic energy loss spectroscopy, optical reflectivity, and conductivity are also performed in the energy range 0 to 70 eV.

Select

Residual compressive stress and intensity of infrared absorption of cubic BN films prepared by plasma enhanced chemical vapor deposition Yang Hang-Sheng (杨杭生), Jin Pan-Pan (金盼盼), Xu Ya-Bo (徐亚伯), Li Hai-Yang (李海洋) Chin. Phys. B, 2014, 23 (3):  037201.  DOI: 10.1088/1674-1056/23/3/037201 Abstract ( 634 )   PDF (425KB) ( 362 )   Theoretical and experimental investigations on the dependence of the intensity of infrared (IR) absorption of polycrystalline cubic boron nitride thin films under the residual compressive stress conditions have been performed. Our results indicate that the intensity of the IR absorption is proportional to the total degree of freedom of all the ions in the ordered regions. The reduction of interstitial Ar atom concentration, which causes the increase in the ordered regions of cubic boron nitride (cBN) crystallites, could be one cause for the increase in the intensity of IR absorption after residual compressive stress relaxation. Theoretical derivation is in good agreement with the experimental results concerning the IR absorption intensity and the Ar interstitial atom concentration in cubic boron nitride films measured by energy dispersion X-ray spectroscopy. Our results also suggest that the interstitial Ar is the origin of residual compressive stress accumulation in plasma enhanced cBN film deposition.

Select

Unidirectional emissions from dielectric photonic circuits decorated with plasmonic phased antenna arrays Hot! Ding Wei (丁伟), Chen Yu-Hui (陈宇辉), Li Zhi-Yuan (李志远) Chin. Phys. B, 2014, 23 (3):  037301.  DOI: 10.1088/1674-1056/23/3/037301 Abstract ( 572 )   PDF (2562KB) ( 533 )   Thanks to resonant characteristics of metallic nanoparticles, optical waves scattered from plasmonic nanoantennae can be well tailored in both amplitude and phase. We numerically demonstrate that, by varying the lengths and the lateral positions of gold nanorods in vicinity of a silicon waveguide, unidirectional emissions with typical forward–backward contrast ratio of 15 dB and directivity of 12 dB can be acquired in a plasmonic phased antenna array with sub-wavelength device length. The properties, i.e., the emission directionality and the size compactness, can be employed to control the far-field radiation pattern from a dielectric photonic circuit. Moreover, by altering the orientations of the dielectric waveguides decorated with plasmonic phased antenna arrays, we propose wireless light transportations in a layered photonic infrastructure, which may have applications in high-density photonic integrations.

Select

Improved mobility of AlGaN channel heterojunction material using an AlGaN/GaN composite buffer layer Wen Hui-Juan (温慧娟), Zhang Jin-Cheng (张进成), Lu Xiao-Li (陆小力), Wang Zhi-Zhe (王之哲), Ha Wei (哈微), Ge Sha-Sha (葛莎莎), Cao Rong-Tao (曹荣涛), Hao Yue (郝跃) Chin. Phys. B, 2014, 23 (3):  037302.  DOI: 10.1088/1674-1056/23/3/037302 Abstract ( 671 )   PDF (878KB) ( 520 )   The quality of an AlGaN channel heterojunction on a sapphire substrate is massively improved by using an AlGaN/GaN composite buffer layer. We demonstrate an Al0.4Ga0.6N/Al0.18Ga0.82N heterojunction with a state-of-the-art mobility of 815 cm2/(V·s) and a sheet resistance of 890 Ω/ under room temperature. The crystalline quality and the electrical properties of the AlGaN heterojunction material are analyzed by atomic force microscopy, high-resolution X-ray diffraction, and van der Pauw Hall and capacitance–voltage (C–V) measurements. The results indicate that the improved electrical properties should derive from the reduced surface roughness and low dislocation density.

Select

Leakage current reduction by thermal oxidation in Ni/Au Schottky contacts on lattice-matched In0.18Al0.82N/GaN heterostructures Lin Fang (林芳), Shen Bo (沈波), Lu Li-Wu (卢励吾), Xu Fu-Jun (许福军), Liu Xin-Yu (刘新宇), Wei Ke (魏珂) Chin. Phys. B, 2014, 23 (3):  037303.  DOI: 10.1088/1674-1056/23/3/037303 Abstract ( 661 )   PDF (524KB) ( 379 )   By using temperature-dependent current–voltage, variable-frequency capacitance–voltage, and Hall measurements, the effects of the thermal oxidation on the electrical properties of Ni/Au Schottky contacts on lattice-matched In0.18Al0.82N/GaN heterostructures are investigated. Decrease of the reverse leakage current down to six orders of magnitude is observed after the thermal oxidation of the In0.18Al0.82N/GaN heterostructures at 700 ℃. It is confirmed that the reverse leakage current is dominated by the Frenkel–Poole emission, and the main origin of the leakage current is the emission of electrons from a trap state near the metal/semiconductor interface into a continuum of electronic states associated with the conductive dislocations in the InxAl1-xN barrier. It is believed that the thermal oxidation results in the formation of a thin oxide layer on the InxAl1-xN surface, which increases the electron emission barrier height.

Select

Finite size effects on helical edge states in HgTe quantum wells with the spin–orbit coupling due to bulk-and structure-inversion asymmetries Cheng Zhi (成志), Zhou Bin (周斌) Chin. Phys. B, 2014, 23 (3):  037304.  DOI: 10.1088/1674-1056/23/3/037304 Abstract ( 624 )   PDF (985KB) ( 582 )   There is a quantum spin Hall state in the inverted HgTe quantum well, characterized by the topologically protected gapless helical edge states lying within the bulk gap. It has been found that for a strip of finite width, the edge states on the two sides can couple together to produce a gap in the spectrum. The phenomenon is called the finite size effect in quantum spin Hall systems. In this paper, we investigate the effects of the spin–orbit coupling due to bulk-and structure-inversion asymmetries on the finite size effect in the HgTe quantum well by means of the numerical diagonalization method. When the bulk-inversion asymmetry is taken into account, it is shown that the energy gap Eg of the edge states due to the finite size effect features an oscillating exponential decay as a function of the strip width of the HgTe quantum well. The origin of this oscillatory pattern on the exponential decay is explained. Furthermore, if the bulk-and structure-inversion asymmetries are considered simultaneously, the structure-inversion asymmetry will induce a shift of the energy gap Eg closing point. Finally, based on the roles of the bulk-and structure-inversion asymmetries on the finite size effects, a way to realize the quantum spin Hall field effect transistor is proposed.

Select

High-efficiency S-band harmonic tuning GaN amplifier Cao Meng-Yi (曹梦逸), Zhang Kai (张凯), Chen Yong-He (陈永和), Zhang Jin-Cheng (张进成), Ma Xiao-Hua (马晓华), Hao Yue (郝跃) Chin. Phys. B, 2014, 23 (3):  037305.  DOI: 10.1088/1674-1056/23/3/037305 Abstract ( 627 )   PDF (419KB) ( 830 )   In this paper, we present a high-efficiency S-band gallium nitride (GaN) power amplifier (PA). This amplifier is fabricated based on a self-developed GaN high-electron-mobility transistor (HEMT) with 10 mm gate width on SiC substrate. Harmonic manipulation circuits are presented in the amplifier. The matching networks consist of microstrip lines and discrete components. Open-circuited stub lines in both input and output are used to tune the 2nd harmonic wave and match the GaN HEMT to the highest efficiency condition. The developed amplifier delivers an output power of 48.5 dBm (～ 70 W) with a power-added efficiency (PAE) of 72.2% at 2 GHz in pulse condition. When operating at 1.8–2.2 GHz (20% relative bandwidth), the amplifier provides an output power higher than 48 dBm (～ 65 W), with a PAE over 70% and a power gain above 15 dB. When operating in continuous-wave (CW) operating conditions, the amplifier gives an output power over 46 dBm (40 W) with PAE beyond 60% over the whole operation frequency range.

Select

Revivals of Zitterbewegung in the Bernevig–Hughes–Zhang model in the quantum spin Hall regime with a laser pulse Wang Yi-Xiang (王义翔), Wu Ya-Min (吴亚敏) Chin. Phys. B, 2014, 23 (3):  037306.  DOI: 10.1088/1674-1056/23/3/037306 Abstract ( 777 )   PDF (497KB) ( 409 )   We theoretically investigate the Zitterbewegung (ZB) behavior of electrons in the Bernevig–Hughes–Zhang model with a short laser pulse. To obtain a steady picture, we fix the electron on the Landau levels with a magnetic field. The ZB motion and the electromagnetic radiations in the quantum spin Hall regime are given. We find that over a shorter time, the electromagnetic radiations show a quasi-classical cyclotron oscillation, while over a longer time, they exhibit a clear revival picture. The resulting revival time and excited electric field are large enough to make experimental detection accessible.

Select

First-principles study of orbital ordering in cubic fluoride KCrF3 Ming Xing (明星), Xiong Liang-Bin (熊良斌), Xu Huo-Xi (徐火希), Du Fei (杜菲), Wang Chun-Zhong (王春忠), Chen Gang (陈岗) Chin. Phys. B, 2014, 23 (3):  037401.  DOI: 10.1088/1674-1056/23/3/037401 Abstract ( 796 )   PDF (375KB) ( 528 )   Comprehensive first-principles calculations are performed to provide insight into the intriguing physical properties of the ternary cubic fluoride KCrF3. The electronic structures exhibit a prominent dependence on the effective local Coulomb interaction parameter Ueff. The ground state of the cubic phase is a ferromagnetic (FM) half-metal with Ueff equal to 0, 2, and 4 eV, whereas the insulating A-type antiferromagnetic (A-AFM) state with concomitant homogeneous orbital ordering is more robust than the FM state for Ueff exceeding 4 eV. We propose that the origin of the orbital ordering is purely electronic when the cooperative Jahn–Teller distortions are absent in cubic KCrF3.

Select

Ho and Ti co-doped BiFeO3 multiferroic ceramics with enhanced magnetization and ultrahigh electrical resistivity Gu Yan-Hong (谷艳红), Liu Yong (刘雍), Yao Chao (姚超), Ma Yan-Wei (马衍伟), Wang Yu (王雨), Chan Helen Lai-Wah (陈王丽华), Chen Wan-Ping (陈万平) Chin. Phys. B, 2014, 23 (3):  037501.  DOI: 10.1088/1674-1056/23/3/037501 Abstract ( 615 )   PDF (906KB) ( 624 )   Bi0.9Ho0.1Fe0.95O3 and Bi0.9Ho0.1Fe0.9Ti0.05O3 ceramics were prepared and compared to reveal the effects of Ho and Ti codoping in BiFeO3. X-ray diffraction indicated that both ceramics had a high rhombohedral perovskite phase content, and microstructural analyses showed that the grains of the Bi0.9Ho0.1Fe0.9Ti0.05O3 ceramics were much smaller than those of Bi0.9Ho0.1Fe0.95O3. An electrical resistivity of more than 1×1014 Ω·cm at room temperature, and a magnetic hysteresis loop with a remnant magnetization 2Mr of ～0.485 emu/g were obtained for Bi0.9Ho0.1Fe0.9Ti0.05O3; both were much higher than those of Bi0.9Ho0.1Fe0.95O3. Changes in the defect subsystem of BiFeO3 induced by Fe-deficiency and (Ho,Ti) codoping are proposed as being responsible for the improvement in the properties.

Select

Thermodynamic properties of Heisenberg magnetic systems Qin Wei (秦伟), Wang Huai-Yu (王怀玉), Long Gui-Lu (龙桂鲁) Chin. Phys. B, 2014, 23 (3):  037502.  DOI: 10.1088/1674-1056/23/3/037502 Abstract ( 469 )   PDF (462KB) ( 537 )   In this paper, we present a comprehensive investigation of the effects of the transverse correlation function (TCF) on the thermodynamic properties of Heisenberg antiferromagnetic (AFM) and ferromagnetic (FM) systems with cubic lattices. The TCF of an FM system is positive and increases with temperature, while that of an AFM system is negative and decreases with temperature. The TCF lowers internal energy, entropy and specific heat. It always raises the free energy of an FM system but raises that of an AFM system only above a specific temperature when the spin quantum number is S≥1. Comparisons between the effects of the TCFs on the FM and AFM systems are made where possible.

TOPICAL REVIEW—Magnetism, magnetic materials, and interdisciplinary research

Select

Magnetic iron oxide nanoparticles：Synthesis and surface coating techniques for biomedical applications Sun Sheng-Nan (孙圣男), Wei Chao (魏超), Zhu Zan-Zan (朱赞赞), Hou Yang-Long (侯仰龙), Subbu S Venkatraman, Xu Zhi-Chuan (徐梽川) Chin. Phys. B, 2014, 23 (3):  037503.  DOI: 10.1088/1674-1056/23/3/037503 Abstract ( 1927 )   PDF (4676KB) ( 14992 )   Iron oxide nanoparticles are the most popular magnetic nanoparticles used in biomedical applications due to their low cost, low toxicity, and unique magnetic property. Magnetic iron oxide nanoparticles, including magnetite (Fe3O4) and maghemite (γ-Fe2O3), usually exhibit a superparamagnetic property as their size goes smaller than 20 nm, which are often denoted as superparamagnetic iron oxide nanoparticles (SPIONs) and utilized for drug delivery, diagnosis, therapy, and etc. This review article gives a brief introduction on magnetic iron oxide nanoparticles in terms of their fundamentals of magnetism, magnetic resonance imaging (MRI), and drug delivery, as well as the synthesis approaches, surface coating, and application examples from recent key literatures. Because the quality and surface chemistry play important roles in biomedical applications, our review focuses on the synthesis approaches and surface modifications of iron oxide nanoparticles. We aim to provide a detailed introduction to readers who are new to this field, helping them to choose suitable synthesis methods and to optimize the surface chemistry of iron oxide nanoparticles for their interests.

CONDENSED MATTER: ELECTRONIC STRUCTURE, ELECTRICAL, MAGNETIC, AND OPTICAL PROPERTIES

Select

Pressure effects on magnetic properties and martensitic transformation of Ni–Mn–Sn magnetic shape memory alloys Zhang Ya-Zhuo (张雅卓), Cao Jia-Mu (曹伽牧), Tan Chang-Long (谭昌龙), Cao Yi-Jiang (曹一江), Cai Wei (蔡伟) Chin. Phys. B, 2014, 23 (3):  037504.  DOI: 10.1088/1674-1056/23/3/037504 Abstract ( 596 )   PDF (341KB) ( 538 )   The mechanism for the effects of pressure on the magnetic properties and the martensitic transformation of Ni–Mn–Sn shape memory alloys is revealed by first-principles calculations. It is found that the total energy difference between paramagnetic and ferromagnetic austenite states plays an important role in the magnetic transition of Ni–Mn–Sn under pressure. The pressure increases the relative stability of the martensite with respect to the austenite, leading to an increase of the martensitic transformation temperature. Moreover, the effects of pressure on the magnetic properties and the martensitic transformation are discussed based on the electronic structure.

Select

Co1-xZnxFe2O4 nanofiber：Synthesized by electrospinning and its magnetic properties Dai Jian-Feng (戴剑锋), Lu Rui-E (路瑞娥), Fu Bi (付比), Gao Kun (高锟), Zhang Liang-Liang (张亮亮) Chin. Phys. B, 2014, 23 (3):  037505.  DOI: 10.1088/1674-1056/23/3/037505 Abstract ( 462 )   PDF (773KB) ( 385 )   Well-aligned and uniform Co0.8Zn0.2Fe2O4 nanofibers (NFs) are prepared by electrospinning via sol–gel and subsequent heat treatment. Each of the as-spun NFs has a diameter of about 300 nm and a smooth surface morphology. The scanning electron microscope (SEM) image shows that the diameter decreases to 70 nm after the Co0.8Zn0.2Fe2O4 NF has been annealed at 650 ℃ for 3 h. The structure and chemical of Co0.8Zn0.2Fe2O4 NF are investigated by X-ray diffraction (XRD) and energy dispersive X-ray spectroscopy (EDS), respectively. Single phase cubic spinel structure, Co0.8Zn0.2Fe2O4 NF, is successfully obtained after having been calcined at 550 ℃ in air for 3 h, and a reduced lattice constant of the Co0.8Zn0.2Fe2O4 NF provides the evidence of effective Zn2+ substitution. The magnetic measurements show that the substitution of Zn2+ for Co2+, i.e., the introduction of non-magnetic Zn2+ ions into A sites, can increase the saturation magnetization (Ms) and reduce the coercivity (Hc). The obtained Hc results of different samples reveal that the critical single-domain size of the Co0.8Zn0.2Fe2O4 NF is approximately 44 nm. By doping Zn2+ with different concentrations, the morphologies of Co1-xZnxFe2O4 (0≤ x ≤ 0.5) NFs do not show obvious changes. For magnetic properties, the Ms increases and Hc decreases monotonically, respectively.

Select

Effect of heating treatment on trap level distribution in polyamide 66 film electrets Xu Pei (徐佩), Zhang Xing-Yuan (张兴元) Chin. Phys. B, 2014, 23 (3):  037701.  DOI: 10.1088/1674-1056/23/3/037701 Abstract ( 681 )   PDF (314KB) ( 346 )   The effect of heating treatment on the trap level distribution in polyamide 66 film electret is studied by thermally stimulated depolarization current (TSDC) technique. For annealed polyamide 66, there are three trap levels that respectively originate from space charge trapped in amorphous phase, interphase and crystalline phase. There is one peak that originates from space charge trapped in amorphous phase for quenched one. Using multi-point method to fit the experimental curves, the detrapping current peaks can be separated and the trap depth is obtained. The shallower trap levels trapped in amorphous phase and interphase are obviously close to the deeper trap level trapped in crystalline phase for annealed polyamide 66 as the polarization temperature increases, while the trap level distribution remains unaffected by polarization temperature for quenched one.

Select

Speckle intensity images of target based on Monte Carlo method Wu Ying-Li (武颖丽), Wu Zhen-Sen (吴振森) Chin. Phys. B, 2014, 23 (3):  037801.  DOI: 10.1088/1674-1056/23/3/037801 Abstract ( 762 )   PDF (1630KB) ( 390 )   Speckle intensity in the detector plane is deduced in the free-space optical system and imaging system based on Van Cittert–Zernike theorem. The speckle intensity images of plane target and conical target are obtained by using the Monte Carlo method and measured experimentally. The results show that when the range extent of target is smaller, the speckle size along the same direction become longer, and the speckle size increase with increasing incident light wavelengths. The speckle size increases and the speckle intensity images of target is closer to the actual object when the aperture scale augments. These findings are useful to access the target information by speckle in laser radar systems.

Select

Theoretical research on electron beam modulation in a field-emission cold cathode electron gun Li Xing-Xing (李兴兴), Yuan Xue-Song (袁学松), Zhang Yu (张宇), Yan Yang (鄢扬) Chin. Phys. B, 2014, 23 (3):  037901.  DOI: 10.1088/1674-1056/23/3/037901 Abstract ( 696 )   PDF (579KB) ( 735 )   In order to develop miniaturized and integrated electron vacuum devices, the electron beam modulation in a field-emission (FE) electron gun based on carbon nanotubes is researched. By feeding a high-frequency field between the cathode and the anode, the steady FE electron beam can be modulated in the electron gun. The optimal structure of the electron gun is discovered using 3D electromagnetism simulation software, and the FE electron gun is simulated by PIC simulation software. The results show that a broadband (74–114 GHz) modulation can be achieved by the electron gun with a rhombus channel, and the modulation amplitude of the beam current increases with the increases in the input power and the electrostatic field.

INTERDISCIPLINARY PHYSICS AND RELATED AREAS OF SCIENCE AND TECHNOLOGY

Select

Coupling interaction between a single emitter and the propagating surface plasmon polaritons in a graphene microribbon waveguide Zhang Lei (张磊), Fu Xiu-Li (符秀丽), Lei Ming (雷鸣), Chen Jian-Jun (陈建军), Yang Jun-Zhong (杨俊忠), Peng Zhi-Jian (彭志坚), Tang Wei-Hua (唐为华) Chin. Phys. B, 2014, 23 (3):  038101.  DOI: 10.1088/1674-1056/23/3/038101 Abstract ( 698 )   PDF (2420KB) ( 1084 )   The coupling interaction between an individual optical emitter and the propagating surface plasmon polaritons in a graphene microribbon (GMR) waveguide is investigated by numerical calculations, where the emitter is situated above the GMR or in the same plane of the GMR. The results reveal a multimode coupling mechanism for the strong interaction between the emitter and the propagating plasmonic waves in graphene. When the emitter is situated in the same plane of the GMR, the decay rate from the emitter to the surface plasmon polaritons increases more than 10 times compared with that in the case with the emitter above the GMR.

TOPICAL REVIEW—Magnetism, magnetic materials, and interdisciplinary research

Select

From self-assembly to quantum guiding：A review of magnetic atomic structures on noble metal surfaces Cao Rong-Xing (曹荣幸), Zhang Xiao-Pu (张孝谱), Miao Bing-Feng (缪冰锋), Sun Liang (孙亮), Wu Di (吴镝), You Biao (游彪), Ding Hai-Feng (丁海峰) Chin. Phys. B, 2014, 23 (3):  038102.  DOI: 10.1088/1674-1056/23/3/038102 Abstract ( 732 )   PDF (2652KB) ( 671 )   Recent advances in the study of magnetic atomic structures on noble metal surfaces are reviewed. These include one-dimensional strings, two-dimensional hexagonal superlattices, and novel structures stabilized by quantum guiding. The combined techniques of low-temperature scanning tunneling microscopy, kinetic Monte Carlo simulations, and ab initio calculations reveal that surface-state-mediated adatom-step and adatom-adatom interactions are the driving forces for selfassembly of these structures. The formation conditions are further discussed by comparing various experimental systems and the kinetic Monte Carlo simulations. Using scanning tunneling spectroscopy and tight-binding calculations together, we reveal that the spectra of these well-ordered structures have characteristic peaks induced by electronic scattering processes of the atoms within the local environment. Moreover, it is demonstrated that quantum confinement by means of nano-size corrals has significant influence on adatom diffusion and self-assembly, leading to a quantum-guided self-assembly.

INTERDISCIPLINARY PHYSICS AND RELATED AREAS OF SCIENCE AND TECHNOLOGY

Select

Enhancing visible-light photocatalytic activity of α-Bi2O3 via non-metal N and S doping Shang Jun (尚军), Gao Yuan (高远), Hao Wei-Chang (郝维昌), Jing Xi (井溪), Xin Hui-Ju (信会菊), Wang Liang (王亮), Feng Hai-Feng (冯海凤), Wang Tian-Min (王天民) Chin. Phys. B, 2014, 23 (3):  038103.  DOI: 10.1088/1674-1056/23/3/038103 Abstract ( 692 )   PDF (920KB) ( 614 )   In recent years, some important research indicated that the visible-light activity of photocatalysts could be enhanced via incorporating p-block non-metal elements into the lattice. In this paper, we investigated the electronic structures of pure and different non-metal (C, N, S, F, Cl, and Br) doped α-Bi2O3 using first-principles calculations based on the density functional theory. The band structures, the electronic densities of states, and the effective masses of electrons and holes for doped α-Bi2O3 were obtained and analyzed. The N and S dopings narrowed the band gap and reduced the effective mass of the carriers, which are beneficial for the photocatalytic performance. The theoretical predication was further confirmed by the experimental results.

Select

Dendrite to symmetry-broken dendrite transition in directional solidification of non-axially oriented crystals Xing Hui (邢辉), Wang Jian-Yuan (王建元), Chen Chang-Le (陈长乐), Jin Ke-Xin (金克新), Du Li-Fei (杜立飞) Chin. Phys. B, 2014, 23 (3):  038104.  DOI: 10.1088/1674-1056/23/3/038104 Abstract ( 700 )   PDF (2626KB) ( 476 )   In this paper, the morphological transition from dendrite to symmetry-broken dendrite is investigated in the directional solidification of non-axially-oriented crystals using a quantitative phase-field model. The effects of pulling velocity and crystal orientation on the morphological transition are investigated. The results indicate the orientation dependence of the symmetry-broken double dendrites. A dendrite to symmetry-broken dendrite transition is found by varying the pulling velocity at different crystal orientations and the symmetry-broken multiple dendrites emerge as a transition state for the symmetry-broken double dendrites. The state region during the transition can be well characterized through the variations of the characteristic angle and the average primary dendritic spacing.

Select

Residual stress induced wetting variation on electric brush-plated Cu film Meng Ke-Ke (孟可可), Jiang Yue (江月), Jiang Zhong-Hao (江忠浩), Lian Jian-She (连建设), Jiang Qing (蒋青) Chin. Phys. B, 2014, 23 (3):  038201.  DOI: 10.1088/1674-1056/23/3/038201 Abstract ( 603 )   PDF (1067KB) ( 352 )   Nanocrystalline Cu film with a mirror surface finishing is prepared by the electric brush-plating technique. The as-prepared Cu film exhibits a superhydrophilic behavior with an apparent water contact angle smaller than 10°. A subsequent increase in the water contact angle and a final wetting transition from inherent hydrophilicity with water contact angle smaller than 90° to apparent hydrophobicity with water contact angle larger than 90° are observed when the Cu film is subjected to natural aging. Analysis based on the measurement of hardness with nanoindentation and the theory of the bond-order-length-strength correlation reveals that this wetting variation on the Cu film is attributed to the relaxation of residual stress generated during brush-plating deposition and a surface hydrophobization role associated with the broken bond polarization induced by surface nanostructure.

Select

Self-consistent field theory of adsorption of flexible polyelectrolytes onto an oppositely charged sphere Tong Zhao-Yang (童朝阳), Zhu Yue-Jin (诸跃进), Tong Chao-Hui (童朝晖) Chin. Phys. B, 2014, 23 (3):  038202.  DOI: 10.1088/1674-1056/23/3/038202 Abstract ( 567 )   PDF (282KB) ( 412 )   The adsorption of flexible polyelectrolyte (PE) with the smeared charge distribution onto an oppositely charged sphere immersed in a PE solution is studied numerically with the continuum self-consistent field theory. The power law scaling relationships between the boundary layer thickness and the surface charge density and the charge fraction of PE chains revealed in the study are in good agreement with the existing analytical result. The curvature effect on the degree of charge compensation of the total amount of charges on the adsorbed PE chains over the surface charges is examined, and a clear understanding of it based on the dependences of the degree of charge compensation on the surface charge density and the charge fraction of PE chains is established.

Select

Reduction of signal reflection along through silicon via channel in high-speed three-dimensional integration circuit Liu Xiao-Xian (刘晓贤), Zhu Zhang-Ming (朱樟明), Yang Yin-Tang (杨银堂), Wang Feng-Juan (王凤娟), Ding Rui-Xue (丁瑞雪) Chin. Phys. B, 2014, 23 (3):  038401.  DOI: 10.1088/1674-1056/23/3/038401 Abstract ( 749 )   PDF (371KB) ( 1042 )   The through silicon via (TSV) technology has proven to be the critical enabler to realize a three-dimensional (3D) gigscale system with higher performance but shorter interconnect length. However, the received digital signal after transmission through a TSV channel, composed of redistribution layers (RDLs), TSVs, and bumps, is degraded at a high data-rate due to the non-idealities of the channel. We propose the Chebyshev multisection transformers to reduce the signal reflection of TSV channel when operating frequency goes up to 20 GHz, by which signal reflection coefficient (S11) and signal transmission coefficient (S21) are improved remarkably by 150% and 73.3%, respectively. Both the time delay and power dissipation are also reduced by 4% and 13.3%, respectively. The resistance-inductance-conductance-capacitance (RLGC) elements of the TSV channel are iterated from scattering (S)-parameters, and the proposed method of weakening the signal reflection is verified using high frequency simulator structure (HFSS) simulation software by Ansoft.

Select

Through-silicon-via crosstalk model and optimization design for three-dimensional integrated circuits Qian Li-Bo (钱利波), Zhu Zhang-Ming (朱樟明), Xia Yin-Shui (夏银水), Ding Rui-Xue (丁瑞雪), Yang Yin-Tang (杨银堂) Chin. Phys. B, 2014, 23 (3):  038402.  DOI: 10.1088/1674-1056/23/3/038402 Abstract ( 655 )   PDF (1282KB) ( 676 )   Through-silicon-via (TSV) to TSV crosstalk noise is one of the key factors affecting the signal integrity of three-dimensional integrated circuits (3D ICs). Based on the frequency dependent equivalent electrical parameters for the TSV channel, an analytical crosstalk noise model is established to capture the TSV induced crosstalk noise. The impact of various design parameters including insulation dielectric, via pitch, via height, silicon conductivity, and terminal impedance on the crosstalk noise is analyzed with the proposed model. Two approaches are proposed to alleviate the TSV noise, namely, driver sizing and via shielding, and the SPICE results show 241 mV and 379 mV reductions in the peak noise voltage, respectively.

Select

Low-leakage-current AlGaN/GaN HEMTs on Si substrates with partially Mg-doped GaN buffer layer by metal organic chemical vapor deposition Li Ming (黎明), Wang Yong (王勇), Wong Kai-Ming (王凯明), Lau Kei-May (刘纪美) Chin. Phys. B, 2014, 23 (3):  038403.  DOI: 10.1088/1674-1056/23/3/038403 Abstract ( 797 )   PDF (1317KB) ( 931 )   High-performance low-leakage-current AlGaN/GaN high electron mobility transistors (HEMTs) on silicon (111) substrates grown by metal organic chemical vapor deposition (MOCVD) with a novel partially Magnesium (Mg)-doped GaN buffer scheme have been fabricated successfully. The growth and DC results were compared between Mg-doped GaN buffer layer and a unintentionally one. A 1-μm gate-length transistor with Mg-doped buffer layer exhibited an OFF-state drain leakage current of 8.3×10-8 A/mm, to our best knowledge, which is the lowest value reported for MOCVD-grown AlGaN/GaN HEMTs on Si featuring the same dimension and structure. The RF characteristics of 0.25-μm gate length T-shaped gate HEMTs were also investigated.

Select

Analysis and modeling of resistive switching mechanism oriented to fault tolerance of resistive memory based on memristor Huang Da (黄达), Wu Jun-Jie (吴俊杰), Tang Yu-Hua (唐玉华) Chin. Phys. B, 2014, 23 (3):  038404.  DOI: 10.1088/1674-1056/23/3/038404 Abstract ( 612 )   PDF (287KB) ( 735 )   With the progress of the semiconductor industry, resistive memories, especially the memristor, have drawn increasing attention. The resistive memory based on memrsitor has not been commercialized mainly because of data error. Currently, there are more studies focused on fault tolerance of resistive memory. This paper studies the resistive switching mechanism which may have time-varying characteristics. Resistive switching mechanism is analyzed and its respective circuit model is established based on the memristor Spice model.

Select

UV-ozone-treated MoO3 as the hole-collecting buffer layer for high-efficiency solution-processed SQ：PC71BM photovoltaic devices Yang Qian-Qian (杨倩倩), Yang Dao-Bin (杨道宾), Zhao Su-Ling (赵谡玲), Huang Yan (黄艳), Xu Zheng (徐征), Gong Wei (龚伟), Fan Xing (樊星), Liu Zhi-Fang (刘志方), Huang Qing-Yu (黄清雨), Xu Xu-Rong (徐叙瑢) Chin. Phys. B, 2014, 23 (3):  038405.  DOI: 10.1088/1674-1056/23/3/038405 Abstract ( 603 )   PDF (552KB) ( 350 )   The enhanced performance of a squaraine compound, with 2,4-bis[4-(N,N-diisobutylamino)-2,6-dihydroxyphenyl] squaraine as the donor and [6,6]-phenyl-C71-butyric acid methyl ester (PC71BM) as the acceptor, in solution-processed organic photovoltaic devices is obtained by using UV-ozone-treated MoO3 as the hole-collecting buffer layer. The optimized thickness of the MoO3 layer is 8 nm, at which the device shows the best power conversion efficiency (PCE) among all devices, resulting from a balance of optical absorption and charge transport. After being treated by UV-ozone for 10 min, the transmittance of the MoO3 film is almost unchanged. Atomic force microscopy results show that the treated surface morphology is improved. A high PCE of 3.99% under AM 1.5 G illumination (100 mW/cm2) is obtained.

Select

100-nm T-gate InAlAs/InGaAs InP-based HEMTs with fT=249 GHz and fmax=415 GHz Wang Li-Dan (汪丽丹), Ding Peng (丁芃), Su Yong-Bo (苏永波), Chen Jiao (陈娇), Zhang Bi-Chan (张毕禅), Jin Zhi (金智) Chin. Phys. B, 2014, 23 (3):  038501.  DOI: 10.1088/1674-1056/23/3/038501 Abstract ( 706 )   PDF (1135KB) ( 949 )   InAlAs/InGaAs high electron mobility transistors (HEMTs) on an InP substrate with well-balanced cutoff frequency fT and maximum oscillation frequency fmax are reported. An InAlAs/InGaAs HEMT with 100-nm gate length and gate width of 2×50 μm shows excellent DC characteristics, including full channel current of 724 mA/mm, extrinsic maximum transconductance gm.max of 1051 mS/mm, and drain–gate breakdown voltage BVDG of 5.92 V. In addition, this device exhibits fT=249 GHz and fmax=415 GHz. These results were obtained by fabricating an asymmetrically recessed gate and minimizing the parasitic resistances. The specific Ohmic contact resistance was reduced to 0.031 Ω·mm. Moreover, the fT obtained in this work is the highest ever reported in 100-nm gate length InAlAs/InGaAs InP-based HEMTs. The outstanding gm.max, fT, fmax, and good BVDG make the device suitable for applications in low noise amplifiers, power amplifiers, and high speed circuits.

Select

A two-dimensional analytical subthreshold behavior model for junctionless dual-material cylindrical surrounding-gate MOSFETs Li Cong (李聪), Zhuang Yi-Qi (庄奕琪), Zhang Li (张丽), Jin Gang (靳刚) Chin. Phys. B, 2014, 23 (3):  038502.  DOI: 10.1088/1674-1056/23/3/038502 Abstract ( 553 )   PDF (514KB) ( 504 )   A two-dimensional analytical subthreshold behavior model for junctionless dual-material cylindrical surrounding-gate (JLDMCSG) metal-oxide-semiconductor field-effect transistors (MOSFETs) is proposed. It is derived by solving the two-dimensional Poisson’s equation in two continuous cylindrical regions with any simplifying assumption. Using this analytical model, the subthreshold characteristics of JLDMCSG MOSFETs are investigated in terms of channel electrostatic potential, horizontal electric field, and subthreshold current. Compared to junctionless single-material cylindrical surrounding-gate MOSFETs, JLDMCSG MOSFETs can effectively suppress short-channel effects and simultaneously improve carrier transport efficiency. It is found that the subthreshold current of JLDMCSG MOSFETs can be significantly reduced by adopting both a thin oxide and thin silicon channel. The accuracy of the analytical model is verified by its good agreement with the three-dimensional numerical simulator ISE TCAD.

Select

Low on-resistance high-voltage lateral double-diffused metal oxide semiconductor with a buried improved super-junction layer Wu Wei (伍伟), Zhang Bo (张波), Luo Xiao-Rong (罗小蓉), Fang Jian (方健), Li Zhao-Ji (李肇基) Chin. Phys. B, 2014, 23 (3):  038503.  DOI: 10.1088/1674-1056/23/3/038503 Abstract ( 601 )   PDF (749KB) ( 638 )   A novel low specific on-resistance (Ron,sp) lateral double-diffused metal oxide semiconductor (LDMOS) with a buried improved super-junction (BISJ) layer is proposed. A super-junction layer is buried in the drift region and the P pillar is split into two parts with different doping concentrations. Firstly, the buried super-junction layer causes the multiple-direction assisted depletion effect. The drift region doping concentration of the BISJ LDMOS is therefore much higher than that of the conventional LDMOS. Secondly, the buried super-junction layer provides a bulk low on-resistance path. Both of them reduce Ron,sp greatly. Thirdly, the electric field modulation effect of the new electric field peak introduced by the step doped P pillar improves the breakdown voltage (BV). The BISJ LDMOS exhibits a BV of 300 V and Ron,sp of 8.08 mΩ·cm2 which increases BV by 35% and reduces Ron,sp by 60% compared with those of a conventional LDMOS with a drift length of 15 μm, respectively.

Select

Increased work function in PEDOT：PSS film under ultraviolet irradiation Xing Ying-Jie (邢英杰), Qian Min-Fang (钱旻昉), Guo Deng-Zhu (郭等柱), Zhang Geng-Min (张耿民) Chin. Phys. B, 2014, 23 (3):  038504.  DOI: 10.1088/1674-1056/23/3/038504 Abstract ( 747 )   PDF (338KB) ( 1625 )   An increase of work function (0.3 eV) is achieved by irradiating poly(3,4-ethylenedioxythiophene):poly(styrene sulfonate) (PEDOT:PSS) film in vacuum with 254-nm ultraviolet (UV) light. The mechanism for such an improvement is investigated by photoelectron yield spectroscopy, X-ray photo electron energy spectrum, and field emission technique. Surface oxidation and composition change are found as the reasons for work function increase. The UV-treated PEDOT:PSS film is used as the hole injection layer in a hole-only device. Hole injection is improved by UV-treated PEDOT:PSS film without baring the enlargement of film resistance. Our result demonstrates that UV treatment is more suitable for modifying the injection barrier than UV ozone exposure.

Select

High performance pentacene organic field-effect transistors consisting of biocompatible PMMA/silk fibroin bilayer dielectric Li Hai-Qiang (李海强), Yu Jun-Sheng (于军胜), Huang Wei (黄伟), Shi Wei (施薇), Huang Jiang (黄江) Chin. Phys. B, 2014, 23 (3):  038505.  DOI: 10.1088/1674-1056/23/3/038505 Abstract ( 933 )   PDF (492KB) ( 62442 )   Pentacene organic field-effect transistors (OFETs) based on single-or double-layer biocompatible dielectrics of poly(methyl methacrylate) (PMMA) and/or silk fibroin (SF) are fabricated. Compared with those devices based on single PMMA or SF dielectric or SF/PMMA bilayer dielectric, the OFETs with biocompatible PMMA/SF bilayer dielectric exhibit optimal performance with a high field-effect mobility of 0.21 cm2/Vs and a current on/off ratio of 1.5×104. By investigating the surface morphology of the pentacene active layer through atom force microscopy and analyzing the electrical properties, the performance enhancement is mainly attributed to the crystallization improvement of the pentacene and the smaller interface trap density at the dielectric/organic interface. Meanwhile, a low contact resistance also indicates that a good electrode/organic contact is formed, thereby assisting the performance improvement of the OFET.

Select

Zero-bias high-responsivity high-bandwidth top-illuminated germanium p–i–n photodetectors Li Chong (李冲), Xue Chun-Lai (薛春来), Liu Zhi (刘智), Cheng Bu-Wen (成步文), Li Chuan-Bo (李传波), Wang Qi-Ming (王启明) Chin. Phys. B, 2014, 23 (3):  038506.  DOI: 10.1088/1674-1056/23/3/038506 Abstract ( 641 )   PDF (294KB) ( 656 )   We report efficient zero-bias high-speed top-illuminated p–i–n photodiodes (PDs) with high responsivity fabricated with germanium (Ge) films grown directly on silicon-on-insulator (SOI) substrates. For a 15 μm-diameter device at room temperature, the dark current density was 44.1 mA/cm2 at –1 V. The responsivity at 1.55 μm was 0.30 A/W at 0 V. The saturation of the optical responsivity at 0 V bias revealed that this photodetector allows a complete photo-generated carrier collection without bias. Although the 3-dB bandwidth of the 15-μ-diameter detector was 18.8 GHz at the reverse bias of 0 V, the detector responsivity was improved by one order of magnitude compared with that reported in the literature. Moreover, the dark current of the detector was significantly reduced.

Select

Sixteen-element Ge-on-SOI PIN photo-detector arrays for parallel optical interconnects Li Chong (李冲), Xue Chun-Lai (薛春来), Liu Zhi (刘智), Cheng Bu-Wen (成步文), Wang Qi-Ming (王启明) Chin. Phys. B, 2014, 23 (3):  038507.  DOI: 10.1088/1674-1056/23/3/038507 Abstract ( 575 )   PDF (424KB) ( 459 )   We describe the structure and testing of one-dimensional array parallel-optics photo-detectors with 16 photodiodes of which each diode operates up to 8 Gb/s. The single element is vertical and top illuminated 30-μm-diameter silicon on insulator (Ge-on-SOI) PIN photodetector. High-quality Ge absorption layer is epitaxially grown on SOI substrate by the ultra-high vacuum chemical vapor deposition (UHV-CVD). The photodiode exhibits a good responsivity of 0.20 A/W at a wavelength of 1550 nm. The dark current is as low as 0.36 μA at a reverse bias of 1 V, and the corresponding current density is about 51 mA/cm2. The detector with a diameter of 30 μm is measured at an incident light of 1.55 μm and 0.5 mW, and the 3-dB bandwidth is 7.39 GHz without bias and 13.9 GHz at a reverse bias of 3 V. The 16 devices show a good consistency.

Select

Confinement of spherical colloid particles in a soft fluid membrane tube Zheng Bin (郑斌), Meng Qing-Tian (孟庆田) Chin. Phys. B, 2014, 23 (3):  038701.  DOI: 10.1088/1674-1056/23/3/038701 Abstract ( 553 )   PDF (540KB) ( 282 )   We investigate the structure of multiple spherical particles confined in a soft membrane tube that originally has a cylindrical shape. Assuming an attraction energy between the surface of the spherical particle and the inner wall of the membrane tube, we show that a variety of conformational structures can be stabilized on the basis of analyzing a Helfrich energy for the soft tube. Using a numerical approach, we calculate the phase diagram in terms of basic parameters in the system. Structures that prefer close contact of spheres and structures that contain well separated spheres are found in this calculation.

Select

Reduced aliasing artifacts using shaking projection k-space sampling trajectory Zhu Yan-Chun (朱艳春), Du Jiang (杜江), Yang Wen-Chao (杨文超), Duan Chai-Jie (段侪杰), Wang Hao-Yu (王浩宇), Gao Song (高嵩), Bao Shang-Lian (包尚联) Chin. Phys. B, 2014, 23 (3):  038702.  DOI: 10.1088/1674-1056/23/3/038702 Abstract ( 724 )   PDF (1099KB) ( 1219 )   Radial imaging techniques, such as projection-reconstruction (PR), are used in magnetic resonance imaging (MRI) for dynamic imaging, angiography, and short-T2 imaging. They are less sensitive to flow and motion artifacts, and support fast imaging with short echo times. However, aliasing and streaking artifacts are two main sources which degrade radial imaging quality. For a given fixed number of k-space projections, data distributions along radial and angular directions will influence the level of aliasing and streaking artifacts. Conventional radial k-space sampling trajectory introduces an aliasing artifact at the first principal ring of point spread function (PSF). In this paper, a shaking projection (SP) k-space sampling trajectory was proposed to reduce aliasing artifacts in MR images. SP sampling trajectory shifts the projection alternately along the k-space center, which separates k-space data in the azimuthal direction. Simulations based on conventional and SP sampling trajectories were compared with the same number projections. A significant reduction of aliasing artifacts was observed using the SP sampling trajectory. These two trajectories were also compared with different sampling frequencies. A SP trajectory has the same aliasing character when using half sampling frequency (or half data) for reconstruction. SNR comparisons with different white noise levels show that these two trajectories have the same SNR character. In conclusion, the SP trajectory can reduce the aliasing artifact without decreasing SNR and also provide a way for undersampling reconstruction. Furthermore, this method can be applied to three-dimensional (3D) hybrid or spherical radial k-space sampling for a more efficient reduction of aliasing artifacts.

Select

β-FeSi2 as the bottom absorber of triple-junction thin-film solar cells：A numerical study Yuan Ji-Ren (袁吉仁), Shen Hong-Lie (沈鸿烈), Zhou Lang (周浪), Huang Hai-Bin (黄海宾), Zhou Nai-Gen (周耐根), Deng Xin-Hua (邓新华), Yu Qi-Ming (余启名) Chin. Phys. B, 2014, 23 (3):  038801.  DOI: 10.1088/1674-1056/23/3/038801 Abstract ( 716 )   PDF (368KB) ( 555 )   Using β-FeSi2 as the bottom absorber of triple-junction thin-film solar cells is investigated by a numerical method for widening the long-wave spectral response. The presented results show that the β-FeSi2 subcell can contribute 0.273 V of open-circuit voltage to the a-Si/μc-Si/β-FeSi2 triple-junction thin-film solar cell. The optimized absorber thicknesses for a-Si, μc-Si, and β-FeSi2 subcells are 260 nm, 900 nm, and 40 nm, respectively. In addition, the temperature coefficient of the conversion efficiency of the a-Si/μc-Si/β-FeSi2 cell is -0.308 %/K, whose absolute value is only greater than that of the a-Si subcell. This result indicates that the a-Si/μc-Si/β-FeSi2 triple-junction solar cell has a good temperature coefficient. As a result, using β-FeSi2 as the bottom absorber can improve the thin-film solar cell performance, and the a-Si/μc-Si/β-FeSi2 triple-junction solar cell is a promising structure configuration for improving the solar cell efficiency.

Select

MoO3/Ag/Al/ZnO intermediate layer for inverted tandem polymer solar cells Qing Jian (卿健), Zhong Zhen-Feng (钟镇锋), Liu Yong (刘勇), Li Bao-Jun (李宝军), Zhou Xiang (周翔) Chin. Phys. B, 2014, 23 (3):  038802.  DOI: 10.1088/1674-1056/23/3/038802 Abstract ( 664 )   PDF (385KB) ( 874 )   We report an MoO3/Ag/Al/ZnO intermediate layer connecting two identical bulk heterojunction subcells with a poly(3-hexylthiophene) and [6,6]-phenyl-C61-butyric acid methyl ester (P3HT and PCBM) active layer for inverted tandem polymer solar cells. The highly transparent intermediate layer with an optimized thickness realizes an Ohmic contact between the two subcells for effective charge extraction and recombination. A maximum power conversion efficiency of 3.76% is obtained for the tandem cell under 100 mW/cm2 illumination, which is larger than that of a single cell (3.15%). The open-circuit voltage of the tandem cell (1.18 V) approaches double that of the single cell (0.61 V).

Select

Effective absorption enhancement in small molecule organic solar cells using trapezoid gratings Xiang Chun-Ping (相春平), Jin Yu (金玉), Liu Jie-Tao (刘杰涛), Xu Bin-Zong (许斌宗), Wang Wei-Min (汪卫敏), Wei Xin (韦欣), Song Guo-Feng (宋国峰), Xu Yun (徐云) Chin. Phys. B, 2014, 23 (3):  038803.  DOI: 10.1088/1674-1056/23/3/038803 Abstract ( 663 )   PDF (2934KB) ( 528 )   We demonstrate that the optical absorption is enhanced in small molecule organic solar cells by using a trapezoid grating structure. The enhanced absorption is mainly attributed to both waveguide modes and surface plasmon modes, which is simulated by using finite-difference time-domain method. The simulated results show that the surface plasmon along the semitransparent metallic Ag anode is excited by introducing the periodical trapezoid gratings, which induce the increase of high intensity field in the donor layer. Meanwhile, the waveguide modes result in a high intensity field in acceptor layer. The increase of field improves the absorption of organic solar cells significantly, which is demonstrated by simulating the electrical properties. The simulated results also show that the short-circuit current is increased by 31% in an optimized device, which is supported by the experimental measurement. Experimental result shows that the power conversion efficiency of the grating sample is increased by 7.7%.