Highlights

Please wait a minute...


For selected: Download citations EndNote Ris BibTeX Toggle thumbnails

Select

Two-step growth of 4-inch multilayer MoS2 wafers Yang-Kun Zhang(张养坤), Yu-Chen Wang(王雨辰), Wei Yang(杨威), Dong-Xia Shi(时东霞), Luo-Jun Du(杜罗军), and Guang-Yu Zhang(张广宇) Chin. Phys. B, 2025, 34 (6): 068103.   DOI: 10.1088/1674-1056/adce9f Abstract （163）      PDF （2727KB）（120）       Knowledge map    Molybdenum disulfide (MoS$_{2}$) is an emerging two-dimensional (2D) semiconductor and has great potential for high-end applications beyond the traditional silicon-based electronics. Compared to the monolayers, multilayer MoS$_{2}$ has improved electron mobility and current density, and therefore provides a more promising platform in terms of thin-film transistors, flexible electronic devices, etc. However, the synthesis of large-area, high-quality multilayer MoS$_{2}$ films with controlled layer number remains a challenge. Here, we develop a two-step oxygen-assisted chemical vapor deposition (OA-CVD) methodology for the synthesis of 4-inch MoS$_{2}$ films from monolayer to trilayer on sapphire substrates. The influence of critical growth parameters on the growth of multilayer MoS$_{2}$ is systematically explored, such as the evaporation temperature of MoO$_{3}$ and the flow rate of O$_{2}$. Flexible field-effect transistor (FET) devices fabricated from bilayer/trilayer MoS$_{2}$ show substantial improvements in mobility compared with flexible FETs based on monolayer films.

Select

Multiferroicity and thermal expansion of the layered metal-organic framework [NH4Cl]2[Ni(HCOO)2(NH3)2] Dan Cheng(程丹), Yingjie He(何英杰), Shuang Liu(刘爽), Na Su(苏娜), and Young Sun(孙阳) Chin. Phys. B, 2025, 34 (6): 067505.   DOI: 10.1088/1674-1056/adcaa4 Abstract （127）      PDF （1303KB）（74）       Knowledge map    We have investigated the magnetic, dielectric, pyroelectric, and thermal expansion properties of a layered perovskite metal-organic framework, [NH$_{4}$Cl]$_{2}$[Ni(HCOO)$_{2}$(NH$_{3}$)$_{2}$]. The material undergoes three phase transitions including a canted antiferromagnetic transition at $\sim 36 $ K, and two successive structural transitions around 100 K and 110 K, respectively. The temperature dependence of dielectric permittivity and pyroelectric current suggests that the structural transitions induce weak ferroelectricity along the $c$-axis and antiferroelectricity in the ab plane. A negative thermal expansion along the $c$-axis is observed between two structural phase transitions, which is ascribed to the abnormal shrinkage of interlayer hydrogen bonding length. Moreover, the ferroelectric/antiferroelectric phase transition temperature shifts towards a higher temperature under a magnetic field, suggesting certain magnetoelectric coupling in the paramagnetic phase. Our study suggests that the layered metal-organic frameworks provide a unique playground for exploring exotic physical properties such as multiferroicity and abnormal thermal expansion.

Select

Simple robot swarm with magnetic coupling connections can collaboratively accomplish collective tasks Xingyu Ma(马星宇), Chuyun Wang(汪楚云), Jing Wang(王璟), Huaicheng Chen(陈怀城), Gao Wang(王高), and Liyu Liu(刘雳宇) Chin. Phys. B, 2025, 34 (6): 068701.   DOI: 10.1088/1674-1056/adc666 Abstract （107）      PDF （2887KB）（49）       Knowledge map    The use of robotic swarms to study the properties of active matter is a common experimental approach. In such studies, robots are often required to possess capabilities in computation, storage, perception, and two-dimensional (2D) movement to execute predefined rules. Under these rules, the swarm can accomplish complex tasks, exhibit rich collective states, or demonstrate intriguing phase transition phenomena. However, this study demonstrates how a swarm of spin robots, which only respond to simple ambient light intensity, can be constructed into a collective system capable of performing practical swarm tasks such as phototactic motion, controllable folding, and object transport through weak coupling interactions between individuals. Furthermore, it is proven that this swarm exhibits strong system fault tolerance. This research aims to demonstrate that, beyond the common design of sophisticated individuals and excellent inter-individual interaction rules, appropriate structural and coupling designs can enable individuals without computational capabilities to generate complex collective behaviors and accomplish diverse swarm tasks through cooperation. This provides a research direction for experimental studies of active matter using robotic systems.

Select

Resolving gravitational redshift with sub-millimeter height differences using spin-squeezed optical clocks Deshui Yu(于得水), Jia Zhang(张佳), Shougang Zhang(张首刚), Tiantian Shi(史田田), and Jingbiao Chen(陈景标) Chin. Phys. B, 2025, 34 (5): 054208.   DOI: 10.1088/1674-1056/adca1d Abstract （507）   HTML （12）    PDF （1517KB）（447）       Knowledge map    The phenomenon that a clock at a higher gravitational potential ticks faster than one at a lower potential, also known as gravitational redshift, is one of the classical tests of Einstein's theory of general relativity. Owing to their ultra-high accuracy and stability, state-of-the-art optical lattice clocks have enabled resolving the gravitational redshift with a millimeter-scale height difference. Further reducing the vertical inter-clock separation down to the sub-millimeter level and especially shortening the required measurement time may be achieved by employing spin squeezing. Here, we theoretically investigate the spin-squeezing-enhanced differential frequency comparison between two optical clocks within a lattice-trapped cloud of $^{171}$Yb atoms. The numerical results illustrate that for a sample of $10^{4}$ atoms, the atomic-collision-limited resolution of the vertical separation between two clocks can reach 0.48 mm, corresponding to a fractional gravitational redshift at the $10^{-20}$ level. In addition, the required averaging time may be reduced to less than one hundredth of that of conventional clocks with independent atoms. Our work opens a door to the future spin-squeezing-enhanced test of general relativity.

Select

Scaling corrections in driven critical dynamics: Application to the two-dimensional dimerized quantum Heisenberg model Jing-Wen Liu(刘静雯), Shuai Yin(阴帅), and Yu-Rong Shu(舒玉蓉) Chin. Phys. B, 2025, 34 (5): 057502.   DOI: 10.1088/1674-1056/adc672 Abstract （282）   HTML （0）    PDF （799KB）（246）       Knowledge map    Driven critical dynamics in quantum phase transitions holds significant theoretical importance, and also has practical applications in fast-developing quantum devices. While scaling corrections have been shown to play important roles in fully characterizing equilibrium quantum criticality, their impact on nonequilibrium critical dynamics has not been extensively explored. In this work, we investigate the driven critical dynamics in a two-dimensional quantum Heisenberg model. We find that in this model the scaling corrections arising from both finite system size and finite driving rate must be incorporated into the finite-time scaling form in order to properly describe the nonequilibrium scaling behaviors. In addition, improved scaling relations are obtained from the expansion of the full scaling form. We numerically verify these scaling forms and improved scaling relations for different starting states using the nonequilibrium quantum Monte Carlo algorithm.

Select

Shear viscosity of an ultracold Fermi gas in the BCS-BEC crossover Jing Min(闵靖), Xiangchuan Yan(严祥传), Da-Li Sun(孙大立), Lu Wang(王璐), Xin Xie(谢馨), Xizhi Wu(吴熙至), Shi-Guo Peng(彭世国), and Kaijun Jiang(江开军) Chin. Phys. B, 2025, 34 (5): 053103.   DOI: 10.1088/1674-1056/adc403 Abstract （274）   HTML （6）    PDF （610KB）（243）       Knowledge map    We report on the measurement of shear viscosity in an ultracold Fermi gas with variable temperatures and tunable interactions. A quadrupole mode excitation in an isotropic harmonic trap is used to quantify the shear viscosity of the quantum gas within the hydrodynamic regime. The shear viscosity of the system as a function of temperature has been investigated, and the results closely align with calculations in the high-temperature limit utilizing a new definition of the cutoff radius. Through an adiabatic sweep across the Bardeen-Cooper-Schrieffer (BCS) to Bose-Einstein condensate (BEC) crossover, we find that the minimum value of the shear viscosity, as a function of interaction strength, is significantly shifted toward the BEC side. Furthermore, the behavior of the shear viscosity is asymmetric on both sides of the location of the minimum.

Select

Enhancing p-d hybridization via synergistic regulation of spatial and energetic orbital overlaps in Ba-doped LaNiO3 epitaxial films for oxygen evolution activity Yingjia Li(李莹嘉), Xiang Xu(徐翔), Xiaoyu Qiu(邱晓宇), Jie Tu(涂杰), Zijian Chen(陈子健), Yujie Zhou(周雨洁), Zhao Guan(关赵), Youyuan Zhang(张友圆), Wen-Yi Tong(童文旖), Shaohui Xu(徐少辉), Ni Zhong(钟妮), Pinghua Xiang(向平华), Chun-Gang Duan(段纯刚), and Binbin Chen(陈斌斌) Chin. Phys. B, 2025, 34 (5): 057101.   DOI: 10.1088/1674-1056/adc7f8 Abstract （258）   HTML （4）    PDF （2065KB）（169）       Knowledge map    The hybridization between oxygen 2p and transition-metal 3d states largely determines the electronic structure near the Fermi level and related functionalities of transition-metal oxides (TMOs). Considerable efforts have been made to manipulate the p-d hybridization in TMOs by tailoring the spatial orbital overlap via structural engineering. Here, we demonstrate enhanced p-d hybridization in Ba$^{2+}$-doped LaNiO$_{3}$ epitaxial films by simultaneously modifying both the spatial and energetic overlaps between the O-2p and Ni-3d orbitals. Combining x-ray absorption spectroscopy and first-principles calculations, we reveal that the enhanced hybridization stems from the synergistic effects of a reduced charge-transfer energy due to hole injection and an increased spatial orbital overlap due to straightening of Ni-O-Ni bonds. We further show that the enhanced p-d hybridization can be utilized to promote the oxygen evolution activity of LaNiO$_{3}$. This work sheds new insights into the fine-tuning of the electronic structures of TMOs for enhanced functionalities.

Select

SR and NMR studies on the van der Waals cluster magnet Nb3Cl8 Lin Yang(杨林), Detong Wu(吴德桐), Xin Han(韩鑫), Jun Luo(罗军), Bo Liu(刘波), Xiaoyan Ma(马肖燕), Huiqian Luo(罗会仟), Jie Yang(杨杰), Bing Shen(沈冰), Rhea Stewart, Devashibhai Adroja, Youguo Shi(石友国), Rui Zhou(周睿), and Shiliang Li(李世亮) Chin. Phys. B, 2025, 34 (5): 057501.   DOI: 10.1088/1674-1056/adc667 Abstract （209）   HTML （0）    PDF （1417KB）（173）       Knowledge map    The van der Waals cluster magnet Nb$_3$Cl$_8$ has recently been shown to possibly host a quantum-spin-liquid ground state. The Nb ions in this compound form a breathing kagome structure, where the magnetic moment comes from three nearest Nb ions forming a molecular cluster with spin $1/2$. Previous bulk measurements including magnetic susceptibility and specific heat suggested the existence of spinon Fermi surfaces. Here we further probe the spin system by nuclear magnetic resonance (NMR) and muon spin rotation and relaxation (μSR) techniques. We confirm that there is no magnetic long-range order and the dynamical spin fluctuations persist down to 0.075 K. These results provide further evidence that Nb$_3$Cl$_8$ may host a quantum spin liquid.

Select

Synergistic bulk and surface engineering via rapid quenching for high-performance Li-rich layered manganese oxide cathodes Xinyun Xiong(熊馨筠), Sichen Jiao(焦思晨), Qinghua Zhang(张庆华), Luyao Wang(王璐瑶), Kun Zhou(周坤), Bowei Cao(曹博维), Xilin Xu(徐熙林), Xiqian Yu(禹习谦), and Hong Li(李泓) Chin. Phys. B, 2025, 34 (5): 058201.   DOI: 10.1088/1674-1056/adc673 Abstract （191）   HTML （3）    PDF （8343KB）（180）       Knowledge map    Lithium-rich manganese-based cathodes (LRMs) have garnered significant attention as promising candidates for high-energy-density batteries due to their exceptional specific capacity exceeding 300 mAh/g, achieved through synergistic anionic and cationic redox reactions. However, these materials face challenges including oxygen release-induced structural degradation and consequent capacity fading. To address these issues, strategies such as surface modification and bulk phase engineering have been explored. In this study, we developed a facile and cost-effective quenching approach that simultaneously modifies both surface and bulk characteristics. Multi-scale characterization and computational analysis reveal that rapid cooling partially preserves the high-temperature disordered phase in the bulk structure, thereby enhancing the structural stability. Concurrently, Li$^{+}$/H$^{+}$ exchange at the surface forms a robust rock-salt/spinel passivation layer, effectively suppressing oxygen evolution and mitigating interfacial side reactions. This dual modification strategy demonstrates a synergistic stabilization effect. The enhanced oxygen redox activity coexists with the improved structural integrity, leading to superior electrochemical performance. The optimized cathode delivers an initial discharge capacity approaching 307.14 mAh/g at 0.1 C and remarkable cycling stability with 94.12% capacity retention after 200 cycles at 1 C. This study presents a straightforward and economical strategy for concurrent surface-bulk modification, offering valuable insights for designing high-capacity LRM cathodes with extended cycle life.

Select

Unveiling the role of high-order anharmonicity in thermal expansion: A first-principles perspective Tianxu Zhang(张天旭), Kun Zhou(周琨), Yingjian Li(李英健), Chenhao Yi(易晨浩), Muhammad Faizan, Yuhao Fu(付钰豪), Xinjiang Wang(王新江), and Lijun Zhang(张立军) Chin. Phys. B, 2025, 34 (4): 046301.   DOI: 10.1088/1674-1056/adb94c Abstract （444）   HTML （2）    PDF （2041KB）（311）       Knowledge map    Thermal expansion is crucial for various industrial processes and is increasingly the focus of research endeavors aimed at improving material performance. However, it is the continuous advancements in first-principles calculations that have enabled researchers to understand the microscopic origins of thermal expansion. In this study, we propose a coefficient of thermal expansion (CTE) calculation scheme based on self-consistent phonon theory, incorporating the fourth-order anharmonicity. We selected four structures (Si, CaZrF$_{6}$, SrTiO$_{3}$, NaBr) to investigate high-order anharmonicity's impact on their CTEs, based on bonding types. The results indicate that our method goes beyond the second-order quasi-harmonic approximation and the third-order perturbation theory, aligning closely with experimental data. Furthermore, we observed that an increase in the ionicity of the structures leads to a more pronounced influence of high-order anharmonicity on CTE, with this effect primarily manifesting in variations of the Grüneisen parameter. Our research provides a theoretical foundation for accurately predicting and regulating the thermal expansion behavior of materials.

Select

Strain-modulated superconductivity of monolayer Tc2B2 Zhengtao Liu(刘正涛), Zihan Zhang(张子涵), Hao Song(宋昊), Tian Cui(崔田), and Defang Duan(段德芳) Chin. Phys. B, 2025, 34 (4): 047104.   DOI: 10.1088/1674-1056/adb94d Abstract （295）   HTML （0）    PDF （5960KB）（178）       Knowledge map    Two-dimensional (2D) superconductors have attracted significant research interest due to their promising potential applications in optoelectronic and microelectronic devices. Herein, we employ first-principles calculations to predicted a new 2D conventional superconductor, Tc$_{2}$B$_{2}$, demonstrating its stable structural configuration. Remarkably, under biaxial strain, the superconducting transition temperature ($T_{\rm c}$) of Tc$_{2}$B$_{2}$ demonstrates a significant enhancement, achieving 19.5 K under 3% compressive strain and 9.2 K under 11% tensile strain. Our study reveals that strain-induced modifications in Fermi surface topology significantly enhance the Fermi surface nesting effect, which amplifies electron-phonon coupling interactions and consequently elevates $T_{\rm c}$. Additionally, the presence of the Lifshitz transition results in a more pronounced rise in $T_{\rm c}$ under compressive strain compared to tensile strain. These insights offer important theoretical guidance for designing 2D superconductors with high-$T_{\rm c}$ through strain modulation.

Select

All-microwave CZ gate based on fixed-frequency driven coupler Wanpeng Gao(高万鹏), Xiaoliang He(何潇梁), Zhengqi Niu(牛铮琦), Daqiang Bao(包大强), Kuang Liu(刘匡), Junfeng Chen(陈俊锋), Zhen Wang(王镇), and Z. R. Lin(林志荣) Chin. Phys. B, 2025, 34 (4): 040304.   DOI: 10.1088/1674-1056/adb68a Abstract （256）   HTML （0）    PDF （1543KB）（161）       Knowledge map    High-quality entangling gates are crucial for scalable quantum information processing. Implementing all-microwave two-qubit gates on fixed-frequency transmons offers advantages in reducing wiring complexity, but the gate performance is often limited due to the residual $ZZ$ interaction and the frequency crowding problem. Here, we introduce a novel scheme that enables a microwave drive-activated CZ gate compatible with the coupler structure to suppress the residual $ZZ$ interaction. The microwave drive is applied to the coupler and the microwave drive frequency remains far detuned from the system's transition frequency to alleviate the frequency crowding problem. We model the gate process analytically and demonstrate a theoretical gate fidelity up to 99.9% numerically. Our scheme is compatible with current coupler-structure-based circuits, and insensitive to microwave crosstalk, showing a possible path for all-microwave quantum operations at scale.

Select

Electronic structure and carrier mobility of BSb nanotubes Lantian Xue(薛岚天), Chennan Song(宋晨楠), Miaomiao Jian(见苗苗), Qiang Xu(许强), Yuhao Fu(付钰豪), Pengyue Gao(高朋越), and Yu Xie(谢禹) Chin. Phys. B, 2025, 34 (3): 037304.   DOI: 10.1088/1674-1056/adacd3 Abstract （599）   HTML （21）    PDF （1097KB）（545）       Knowledge map    High-mobility semiconductor nanotubes have demonstrated great potential for applications in high-speed transistors, single-charge detection, and memory devices. Here we systematically investigated the electronic properties of single-walled boron antimonide (BSb) nanotubes using first-principles calculations. We observed that rolling the hexagonal boron antimonide monolayer into armchair (ANT) and zigzag (ZNT) nanotubes induces compression and wrinkling effects, significantly modifying the band structures and carrier mobilities through band folding and $\pi^*$-$\sigma^*$ hybridization. As the chiral index increases, the band gap and carrier mobility of ANTs decrease monotonically, where electron mobility consistently exceeds hole mobility. In contrast, ZNTs exhibit a more complex trend: the band gap first increases and then decreases, and the carrier mobility displays oscillatory behavior. In particular, both ANTs and ZNTs could exhibit significantly higher carrier mobilities compared to hexagonal monolayer and zinc-blende BSb, reaching $10^3$-$10^7$ cm$^2\cdot$V$^{-1}\cdot$s$^{-1}$. Our findings highlight strong curvature-induced modifications in the electronic properties of single-walled BSb nanotubes, demonstrating the latter as a promising candidate for high-performance electronic devices.

Select

Anomalous Hall effect in Bernal tetralayer graphene enhanced by spin-orbit interaction Zhuangzhuang Qu(曲壮壮), Zhihao Chen(陈志豪), Xiangyan Han(韩香岩), Zhiyu Wang(王知雨), Zhuoxian Li(李卓贤), Qianling Liu(刘倩伶), Wenjun Zhao(赵文俊), Kenji Watanabe, Takashi Taniguchi, Zhi-Gang Cheng(程智刚), Zizhao Gan(甘子钊), and Jianming Lu(路建明) Chin. Phys. B, 2025, 34 (3): 037201.   DOI: 10.1088/1674-1056/adb411 Abstract （445）   HTML （28）    PDF （4650KB）（370）       Knowledge map    Spin-orbit interaction (SOI) can be introduced by the proximity effect to modulate the electronic properties of graphene-based heterostructures. In this work, we stack trilayer WSe$_{2}$ on Bernal tetralayer graphene to investigate the influence of SOI on the anomalous Hall effect (AHE). In this structurally asymmetric device, by comparing the magnitude of AHE at positive and negative displacement fields, we find that AHE is strongly enhanced by bringing electrons in proximity to the WSe$_{2}$ layer. Meanwhile, the enhanced AHE signal persists up to 80 K, providing important routes for topological device applications at high temperatures.

Select

Manipulation of vortex array via a magnetism-tunable spin-polarized scanning tunnelling microscopy Bing Xia(夏冰), Hong-Yuan Chen(陈虹源), Jian Zheng(郑健), Bo Yang(杨波), Jie Cai(蔡杰), Yi Zhang(章毅), Yi Yang(杨毅), Hao Yang(杨浩), Dan-Dan Guan(管丹丹), Xiao-Xue Liu(刘晓雪), Liang Liu(刘亮), Yao-Yi Li(李耀义), Shi-Yong Wang(王世勇), Can-Hua Liu(刘灿华), Hao Zheng(郑浩), and Jin-Feng Jia(贾金锋) Chin. Phys. B, 2025, 34 (3): 037402.   DOI: 10.1088/1674-1056/adb38d Abstract （384）   HTML （16）    PDF （1457KB）（303）       Knowledge map    Manipulating and braiding Majorana zero modes (MZM) are a critical step toward realizing topological quantum computing. The primary challenge is controlling the vortex, which hosts the MZM, within a superconducting film in a spatially precise manner. To address this, we developed a magnetic force-based vortex control technology using the STM system with a self-designed four-electrode piezo-scanner tube and investigated vortex manipulation on the NbSe$_{2}$ superconducting film. We employed ferromagnetic tips to control the movement of vortex array induced by the tip's remanent magnetism. A magnetic core solenoid device was integrated into the STM system and a strong magnetic tip demagnetization technique was developed, providing a viable technical solution for further enabling single vortex manipulation.

Select

Explosive information spreading in higher-order networks: Effect of social reinforcement Yu Zhou(周宇), Yingpeng Liu(刘英鹏), Liang Yuan(袁亮), Youhao Zhuo(卓友濠), Kesheng Xu(徐克生), Jiao Wu(吴娇), and Muhua Zheng(郑木华) Chin. Phys. B, 2025, 34 (3): 038704.   DOI: 10.1088/1674-1056/adacc8 Abstract （240）   HTML （5）    PDF （1135KB）（194）       Knowledge map    Information spreading has been investigated for many years, but the mechanism of why the information explosively catches on overnight is still under debate. This explosive spreading phenomenon was usually considered driven separately by social reinforcement or higher-order interactions. However, due to the limitations of empirical data and theoretical analysis, how the higher-order network structure affects the explosive information spreading under the role of social reinforcement has not been fully explored. In this work, we propose an information-spreading model by considering the social reinforcement in real and synthetic higher-order networks, describable as hypergraphs. Depending on the average group size (hyperedge cardinality) and node membership (hyperdegree), we observe two different spreading behaviors: (i) The spreading progress is not sensitive to social reinforcement, resulting in the information localized in a small part of nodes; (ii) a strong social reinforcement will promote the large-scale spread of information and induce an explosive transition. Moreover, a large average group size and membership would be beneficial to the appearance of the explosive transition. Further, we display that the heterogeneity of the node membership and group size distributions benefit the information spreading. Finally, we extend the group-based approximate master equations to verify the simulation results. Our findings may help us to comprehend the rapidly information-spreading phenomenon in modern society.

Select

Elastic properties of Cu-6wt% Ag alloy wires for pulsed magnets investigated by ultrasonic techniques Ziyu Li(李滋雨), Tianyi Gu(顾天逸), Wenqi Wei(魏文琦), Yang Yuan(袁洋), Zhuo Wang(王卓), Kangjian Luo(罗康健), Yupeng Pan(潘宇鹏), Jianfeng Xie(谢剑峰), Shaozhe Zhang(张绍哲), Tao Peng(彭涛), Lin Liu(柳林), Qi Chen(谌祺), Xiaotao Han(韩小涛), Yongkang Luo(罗永康), and Liang Li(李亮) Chin. Phys. B, 2025, 34 (2): 020701.   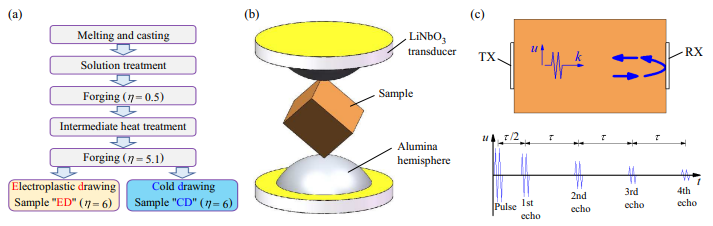DOI: 10.1088/1674-1056/ada1c8 Abstract （593）   HTML （21）    PDF （795KB）（503）       Knowledge map    Conductor materials with good mechanical performance as well as high electrical and thermal conductivities are particularly important to break through the current bottle-neck limit ($\sim 100$ T) of pulsed magnets. Here, we perform systematic studies on the elastic properties of the Cu-6wt% Ag alloy wire, which is a promising candidate material for the new-generation pulsed magnets, by employing two independent ultrasonic techniques, i.e., resonant ultrasound spectroscopy (RUS) and ultrasound pulse-echo experiments. Our RUS measurements manifest that the elastic properties of the Cu-6wt% Ag alloy wires can be improved by an electroplastic drawing procedure as compared with the conventional cold drawing. We also take this opportunity to test the availability of our newly-built ultrasound pulse-echo facility at the Wuhan National High Magnetic Field Center (WHMFC, China), and the results suggest that the elastic performance of the electroplastically-drawn Cu-6wt% Ag alloy wire remains excellent without anomalous softening under extreme conditions, e.g., in ultra-high magnetic field up to 50 T and nitrogen or helium cryogenic liquids.

Select

Evolution from the Kondo phase to the RKKY phase in the small impurity spacing regime of the two-impurity Anderson model Hou-Min Du(杜厚旻) and Yu-Liang Liu(刘玉良) Chin. Phys. B, 2025, 34 (2): 027102.   DOI: 10.1088/1674-1056/ada54f Abstract （370）   HTML （9）    PDF （1118KB）（330）       Knowledge map    Understanding the quantum critical phenomena is one of the most important and challenging tasks in condensed matter physics and the two-impurity Anderson model (TIAM) is a good starting point for this exploration. To this end, we employ the algebraic equation of motion approach to calculate the TIAM and analytically obtain the explicit single-particle impurity Green function under the soft cut-off approximation (SCA). This approach effectively incorporates the impurity spacing as an intrinsic parameter. By solving the pole equations of the Green function, we have, for the first time, qualitatively calculated the spectral weight functions of the corresponding low-energy excitations. We find that when the impurity spacing is less than one lattice distance, the dynamic Rudermann-Kittel-Kasuya-Yosida (RKKY) interaction effectively enters, resulting in a rapid increase in the spectral weights of the RKKY phase, which ultimately surpass those of the Kondo phase; while the spectral weights of the Kondo phase are strongly suppressed. From the perspective of spectral weights, we further confirm the existence of a crossover from the Kondo phase to the RKKY phase in the TIAM. Based on these results, the reasons for the phenomenon of the Kondo resonance splitting are also discussed.

Select

Possible coexistence of superconductivity and topological electronic states in 1T-RhSeTe Tengdong Zhang(张腾东), Rui Fan(樊睿), Yan Gao(高炎), Yanling Wu(吴艳玲), Xiaodan Xu(徐晓丹), Dao-Xin Yao(姚道新), and Jun Li(李军) Chin. Phys. B, 2025, 34 (2): 027403.   DOI: 10.1088/1674-1056/ada432 Abstract （281）   HTML （0）    PDF （1824KB）（274）       Knowledge map    Transition metal dichalcogenides (TMDs), exhibit a range of crystal structures and topological quantum states. The 1T phase, in particular, shows promise for superconductivity driven by electron-phonon coupling (EPC), strain, pressure, and chemical doping. In this theoretical investigation, we explore 1T-RhSeTe as a novel type of TMD superconductor with topological electronic states. The optimal doping structure and atomic arrangement of 1T-RhSeTe are constructed. Phonon spectrum calculations validate the integrity of the constructed doping structure. The analysis of the electron-phonon coupling using the electron-phonon Wannier (EPW) method has confirmed the existence of a robust electron-phonon interaction in 1T-RhSeTe, resulting in total EPC constant $\lambda = 2.02$, the logarithmic average frequency $\omega_{\rm log} = 3.15$ meV and $T_{\rm c} = 4.61$ K, consistent with experimental measurements and indicative of its classification as a BCS superconductor. The band structure analysis revealed the presence of Dirac-like band crossing points. The topological non-trivial electronic structures of the 1T-RhSeTe are confirmed via the evolution of Wannier charge centers (WCCs) and time-reversal symmetry-protected topological surface states (TSSs). These distinctive properties underscore 1T-RhSeTe as a possible candidate for a topological superconductor, warranting further investigation into its potential implications and applications.

Select

Auxiliary-field Monte Carlo method for frustrated spin systems Ning Cai(蔡凝), Yuan Gao(高源), Wei Li(李伟), and Yang Qi(戚扬) Chin. Phys. B, 2025, 34 (2): 027504.   DOI: 10.1088/1674-1056/ada758 Abstract （240）   HTML （5）    PDF （588KB）（239）       Knowledge map    We extend a semiclassical numerical method, bosonic auxiliary-field Monte Carlo, to quantum spin systems. This method breaks the lattice into clusters, solves each cluster precisely and couples them with classical auxiliary fields through classical Monte Carlo simulation. We test the method with antiferromagnetic spin models in one-dimensional chains, square lattices and triangular lattices, and obtain reasonable results at finite temperatures. This algorithm builds a bridge between classical Monte Carlo method and quantum methods. The algorithm can be improved with either progress in classical Monte Carlo sampling or the development of quantum solvers, and can also be further applied to systems with different lattices or interactions.

• page
• Page 1 of 38
• Total 750 records
• First page
• Prev page
• Next page
• Last page