Quantum entanglement of an entangled coherent state：Role of particle losses

doi:10.1088/1674-1056/23/3/030310

Abstract We analyze entanglement properties of entangled coherent state (ECS), |α, 0>_1,2+|0, α >_1,2, with and without photon losses. By separating the coherent state into |α >=c₀|0>+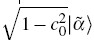

, we derive exact results of the logarithmic negativity E_N, which quantifies the degree of entanglement between the two bosonic modes. Without particle losses, E_N=1 for the N00N state; while for the ECS, E_N increases from 0 to 1 as |α|²→∞. In the presence of photon losses, we find that the ECS with large enough photon number is more robust than that of the N00N state. An optimal ECS is obtained by maximizing E_N with respect to |α|².

Keywords: quantum entanglement entangled coherent state photon losses

Received: 28 June 2013
Revised: 06 August 2013
Accepted manuscript online:

PACS:	03.67.Mn	(Entanglement measures, witnesses, and other characterizations)
	03.65.Ud	(Entanglement and quantum nonlocality)
	42.50.-p	(Quantum optics)

Fund: Project supported by the National Natural Science Foundation of China (Grant No. 11174028), the Fundamental Research Funds for the Central Universities of China (Grant No. 2011JBZ013), and the Program for New Century Excellent Talents in University of China (Grant No. NCET-11-0564).

Corresponding Authors: Jin Guang-Ri
E-mail: grjin@bjtu.edu.cn

Cite this article:

Liu Pan (刘盼), Feng Xiao-Min (冯晓敏), Jin Guang-Ri (金光日) Quantum entanglement of an entangled coherent state：Role of particle losses 2014 Chin. Phys. B 23 030310

[1]	Braunstein S L and van Loock P 2005 Rev. Mod. Phys. 77 513
[2]	Caves C M 1981 Phys. Rev. D 23 1963
[3]	Yurke B, MacCall S L and Klauder J R 1986 Phys. Rev. A 33 4033
[4]	Giovannetti V, Lloyd S and Maccone L 2011 Nat. Photon. 5 222
[5]	Genoni M G, Olivares S and Paris M G A 2011 Phys. Rev. Lett. 106 153603
[6]	Escher B M, Davidovich L, Zagury N and de Matos Filho R L 2012 Phys. Rev. Lett. 109 190404
[7]	Dorner U et al. 2009 Phys. Rev. Lett. 102 040403
[8]	Joo J, Munro W J and Spiller T P 2011 Phys. Rev. Lett. 107 083601
[9]	Leverrier A and Grangier P 2009 Phys. Rev. Lett. 102 180504
[10]	Grosshans F, van Assche G, Wenger J, Brouri R, Cerf N J and Grangier P 2003 Nature 421 238
[11]	Lance A M, Symul T, Sharma V, Weedbrook C, Ralph T C and Lam P K 2005 Phys. Rev. Lett. 95 180503
[12]	Ralph T C and Lam P K 2009 Nature 3 671
[13]	Sanders B C 1992 Phys. Rev. A 45 6811
[14]	Filip R, Rehácek J and Dusek M 2001 J. Opt. B: Quantum Semiclass. Opt. 3 341
[15]	Jeong H, Kim M S and Lee J 2001 Phys. Rev. A 64 052308
[16]	Wang X 2002 J. Phys. A 35 165
[17]	Tara K, Agarwal G S and Chaturvedi S 1993 Phys. Rev. A 47 5024
[18]	van Enk S J 2003 Phys. Rev. Lett. 91 017902
[19]	Paternostro M, Kim M S and Ham B S 2003 Phys. Rev. A 67 023811
[20]	Kuang L M, Chen Z B and Pan J W 2007 Phys. Rev. A 76 052324
[21]	Yu T and Eberly J H 2009 Science 323 598
[22]	Al-Qasimi A and James D F V 2009 Opt. Lett. 34 268
[23]	Ma J, Huang Y, Wang X and Sun C P 2011 Phys. Rev. A 84 022302
[24]	Liu Q G and Ji X 2012 Acta Phys. Sin. 61 230303 (in Chinese)
[25]	Gerry C C and Knight P L 2005 Introductory Quantum Optics (Cambridge: Cambridge University Press)
[26]	van Enk S J 2005 Phys. Rev. A 72 022308
[27]	Wickert R, Bernardes N K and van Loock 2010 Phys. Rev. A 81 062344
[28]	El Allati A, Hassouni Y and Metwally N 2011 Chin. Phys. B 20 110303
[29]	Lastra F, Romero G, Lopez C E, Zagury N and Retamal J C 2010 Opt. Commun. 283 3825
[30]	Vidal G and Werner R F 2002 Phys. Rev. A 65 032314
[31]	Adesso G, Serafini A and Illuminati F 2004 Phys. Rev. A 70 022318
[32]	Boto A N, Kok P, Abrams D S, Braunstein S L, Williams C P and Dowling J P 2000 Phys. Rev. Lett. 85 2733
[33]	Mitchell M W, Lundeen J S and Steinberg A M 2004 Nature 429 161
[34]	Zhang D H, Zhou D L and Fan H 2011 Chin. Phys. Lett. 27 90306
[35]	Agarwal G S, Chaturvedi S and Rai A 2010 Phys. Rev. A 81 043843
[36]	Helstrom C W 1976 Quantum Detection and Estimation Theory (New York: Academic Press)
[37]	Holevo A S 1982 Probabilistic and Statistical Aspect of Quantum Theory (Pisa: North-Holland Press)
[38]	Braunstein S L and Caves C M 1994 Phys. Rev. Lett. 72 3439
[39]	Pezzé L and Smerzi A 2009 Phys. Rev. Lett. 102 100401
[40]	Zhou B Y, Deng L, Duan Y F, Yu L and Li G X 2012 Chin. Phys. B 21 090302
[41]	Obada A S F, Hessian H A, Mohamed A B A and Hashem M 2012 Chin. Phys. B 21 100310

[1]	Entanglement and thermalization in the extended Bose-Hubbard model after a quantum quench: A correlation analysis Xiao-Qiang Su(苏晓强), Zong-Ju Xu(许宗菊), and You-Quan Zhao(赵有权). Chin. Phys. B, 2023, 32(2): 020506.
[2]	Nonreciprocal coupling induced entanglement enhancement in a double-cavity optomechanical system Yuan-Yuan Liu(刘元元), Zhi-Ming Zhang(张智明), Jun-Hao Liu(刘军浩), Jin-Dong Wang(王金东), and Ya-Fei Yu(於亚飞). Chin. Phys. B, 2022, 31(9): 094203.
[3]	Characterizing entanglement in non-Hermitian chaotic systems via out-of-time ordered correlators Kai-Qian Huang(黄恺芊), Wei-Lin Li(李蔚琳), Wen-Lei Zhao(赵文垒), and Zhi Li(李志). Chin. Phys. B, 2022, 31(9): 090301.
[4]	Bright 547-dimensional Hilbert-space entangled resource in 28-pair modes biphoton frequency comb from a reconfigurable silicon microring resonator Qilin Zheng(郑骑林), Jiacheng Liu(刘嘉成), Chao Wu(吴超), Shichuan Xue(薛诗川), Pingyu Zhu(朱枰谕), Yang Wang(王洋), Xinyao Yu(于馨瑶), Miaomiao Yu(余苗苗), Mingtang Deng(邓明堂), Junjie Wu(吴俊杰), and Ping Xu(徐平). Chin. Phys. B, 2022, 31(2): 024206.
[5]	Influences of spin-orbit interaction on quantum speed limit and entanglement of spin qubits in coupled quantum dots M Bagheri Harouni. Chin. Phys. B, 2021, 30(9): 090301.
[6]	Nonlocal advantage of quantum coherence and entanglement of two spins under intrinsic decoherence Bao-Min Li(李保民), Ming-Liang Hu(胡明亮), and Heng Fan(范桁). Chin. Phys. B, 2021, 30(7): 070307.
[7]	Entanglement properties of GHZ and W superposition state and its decayed states Xin-Feng Jin(金鑫锋), Li-Zhen Jiang(蒋丽珍), and Xiao-Yu Chen(陈小余). Chin. Phys. B, 2021, 30(6): 060301.
[8]	Quantifying entanglement in terms of an operational way Deng-Hui Yu(于登辉) and Chang-Shui Yu(于长水). Chin. Phys. B, 2021, 30(2): 020302.
[9]	Reversion of weak-measured quantum entanglement state Shao-Jiang Du(杜少将), Yonggang Peng(彭勇刚), Hai-Ran Feng(冯海冉), Feng Han(韩峰), Lian-Wu Yang(杨连武), Yu-Jun Zheng(郑雨军). Chin. Phys. B, 2020, 29(7): 074202.
[10]	Qubit movement-assisted entanglement swapping Sare Golkar, Mohammad Kazem Tavassoly, Alireza Nourmandipour. Chin. Phys. B, 2020, 29(5): 050304.
[11]	Quantum speed limit time and entanglement in a non-Markovian evolution of spin qubits of coupled quantum dots M. Bagheri Harouni. Chin. Phys. B, 2020, 29(12): 124203.
[12]	Protecting the entanglement of two-qubit over quantum channels with memory via weak measurement and quantum measurement reversal Mei-Jiao Wang(王美姣), Yun-Jie Xia(夏云杰), Yang Yang(杨阳), Liao-Zhen Cao(曹连振), Qin-Wei Zhang(张钦伟), Ying-De Li(李英德), and Jia-Qiang Zhao(赵加强). Chin. Phys. B, 2020, 29(11): 110307.
[13]	Hidden Anderson localization in disorder-free Ising–Kondo lattice Wei-Wei Yang(杨薇薇), Lan Zhang(张欄), Xue-Ming Guo(郭雪明), and Yin Zhong(钟寅)†. Chin. Phys. B, 2020, 29(10): 107301.
[14]	Geometrical quantum discord and negativity of two separable and mixed qubits Tang-Kun Liu(刘堂昆), Fei Liu(刘飞), Chuan-Jia Shan(单传家), Ji-Bing Liu(刘继兵). Chin. Phys. B, 2019, 28(9): 090304.
[15]	Atom interferometers with weak-measurement path detectors and their quantum mechanical analysis Zhi-Yuan Li(李志远). Chin. Phys. B, 2019, 28(6): 060301.

No Suggested Reading articles found!

Viewed

Full text

Abstract

Cited

Metrics
Related Articles

Quantum entanglement of an entangled coherent state：Role of particle losses

Cite this article:

Online attention