† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant Nos. 61176095 and 61404169) and the Youth Innovation Promotion Association of Chinese Academy of Sciences.
The experimental results of the cryogenic temperature characteristics on 0.18-μm silicon-on-insulator (SOI) metal-oxide-silicon (MOS) field-effect-transistors (FETs) were presented in detail. The current and capacitance characteristics for different operating conditions ranging from 300 K to 10 K were discussed. SOI MOSFETs at cryogenic temperature exhibit improved performance, as expected. Nevertheless, operation at cryogenic temperature also demonstrates abnormal behaviors, such as the impurity freeze-out and series resistance effects. In this paper, the critical parameters of the devices were extracted with a specific method from 300 K to 10 K. Accordingly, some temperature-dependent-parameter models were created to improve fitting precision at cryogenic temperature.
Nowadays, cryogenic integrated circuits have aroused great interest as a result of the high enthusiasm for Lunar and Martian exploration. However, the reliability of semiconductor devices to cryogenic environment confront more serious issues. The surprisingly extreme temperature of space background as low as 3 K makes the operation of electronics system quite difficult.[1,2] Presently, spacecraft operating in the cryogenic environment of deep space carries on-board radioisotope heating units to maintain a safe operating temperature for the electronic system.[3] This is not an ideal solution since the required active thermal control system increases cost and complexity. Meanwhile, some indispensable sub-systems such as high-sensitivity cooled sensors are required to operate in cryogenic environment. Particularly, sensors in SOI MOS process show an excellent cryogenic performance compared with bulk MOS process.[4] Hence, devices capable of operation at cryogenic temperatures will not only tolerate the unamiable space environment, but also reduce the weight of craft.
The SOI MOS offers several benefits over bulk MOS technology, such as latch-up immunity, especially in the space application due to its excellent radiation hardness.[5–7] The long-recognized advantages of MOS working at cryogenic temperature have encouraged investigators in many fields all over the world since the 1970s.[8] The main advantages of MOS under cryogenic temperature are associated with an increased carrier mobility, better turn-on capabilities, higher saturation velocity, higher thermal and electrical conductivity, lower power consumption, reduced thermal noise, and decrease of junction leakage currents.[9,10] With liquid nitrogen, Jason investigated the characteristic of bulk MOS.[11] With the increasing miniaturization of microelectronic technology, the experimental results for 0.1-μm MOS were reported in 1987 for the first time.[12] Recently, the reliability of 65-nm MOS was investigated in 2015.[13] The research on SOI technology at cryogenic temperature started a little later than on bulk silicon. Young and Elewa reported the advantages of cryogenic operation of SOI MOS as far back as 1990.[14,15] For the use of sub-20-nm CMOS technology, Shin investigated the characterization of advanced FD-SOI MOS at cryogenic temperature.[16] However, some specific problems related to the cryogenic temperature, such as the impurity freeze-out and series resistance effects, make it difficult for some practical applications. So as to solve some problems, a circuit structure featured twin-gate was proved effective at very low temperature.[17] More recently, Sansen obtained an 8-bit analog-to-digital converter working from 4.2 K to 300 K, guaranteeing the reliability of circuits at cryogenic temperature.[18]
Previous work was always concentrated in the area of cryogenic I–V performance of SOI MOS.[19–21] In this work, the experimental results of cryogenic I–V and C–V performance of SOI MOSFETs with a radiation-hard architecture in a 0.18-μm process are presented. Some specific behaviors at cryogenic temperature are analyzed. More specifically, numerical models of several key parameters are described.
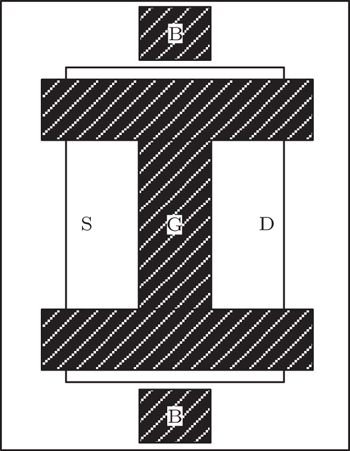
Due to the excellent performance in radiation hardness, devices with H-gate are generally used in the radiation-hard application.[22] In this paper, the devices are H-gate using 0.18 μm PDSOI process as shown in Fig.
To investigate the impact of cryogenic temperature, the gate width and length of the device in our test are both 20 μm to eliminate the effects of a short channel and narrow channel. In order to decrease the effect of noise and gate resistance in C–V test, a multiple fingers gate is utilized. In I–V test we investigated MOSFETs with gate length (L) and width (W) both of 20 μm. In C–V test, the MOSFET of which L and W are 10 μm and 100 μm respectively has 20 fingers. As shown in Fig.
The output characteristics of the NMOSFET (W = 20 μm, L = 20 μm) from room temperature to cryogenic temperature can be seen in Fig.
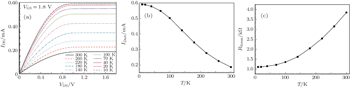 | Fig. 3. (a) Drain current versus VDS; (b) saturation drain current versus temperature; (c) linear resistance versus temperature, from 300 K to 10 K. |
Figures

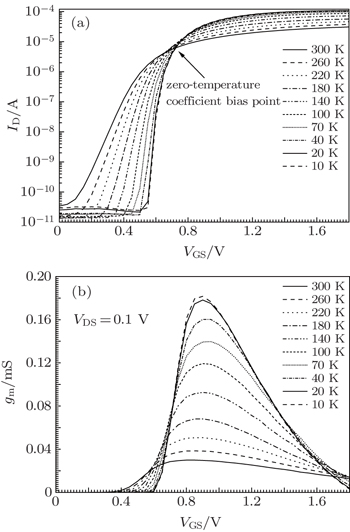 | Fig. 4. (a) Drain current versus gate-to-source voltage; (b) transconductance versus gate-to-source, from 300 K to 10 K. |
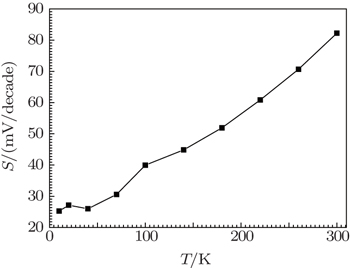
The sub-threshold swing S is defined as
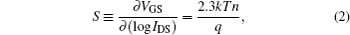
It is very important to maintain the reliability of COX. The C–V characteristic is universally used to measure some important parameters such as the thickness of oxide, Vth, and flatband voltage. In this paper, characterization analysis of MOS capacitors will be carried out at a high frequency of 1 MHz. The C–V test strategy in Keithley 4200 is implemented by applying a small alternating voltage to the MOSFET under test. Q can be derived by integrating the current over time, and C can be calculated from

To get the characteristic of gate-to-bulk capacitance CGB, the nodes gate and bulk of SOI NMOSFET are connected to the semiconductor characterization system, and the node drain and source are opened. The experimental result of CGB versus temperature is shown in Fig.
Starting from about 20 K, a specific behavior was observed and the CGB curves do not coincide with each other at adjacent measurement cycles and finally converge to a certain curve after some test iterations, and the same phenomenon exists in CGB curve of PMOSFET, as shown in Fig.
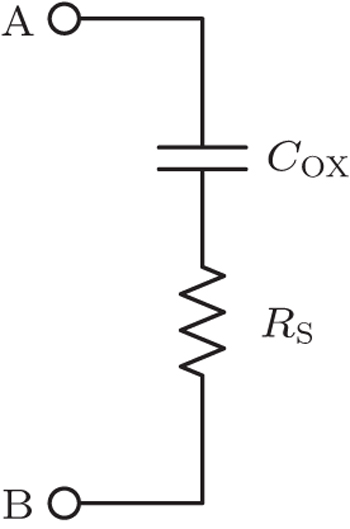
The COX is commonly defined as the capacitance in a strong accumulation region. However, the series resistance Rs is unavoidable in the device of a semiconducting film on a nonconducting substrate. Series resistances in our test mainly arise from the undepleted region between the tunnel and the body tie. To measure series resistance, the simple circuit can be utilized to analyze, as shown in Fig.
The equal capacitance Cm and conductance Gm can be tested by semiconductor characterization system. The admittance Ym across terminals A–B (see Fig.

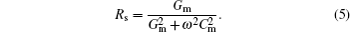
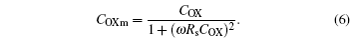
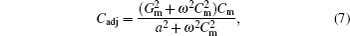

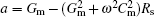
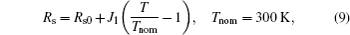
Flatband voltage represents an important parameter that can be derived from flatband capacitance CFB. As is well known, CFB is calculated as[11]

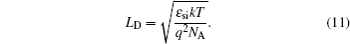



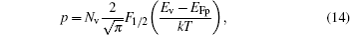
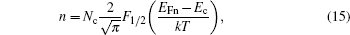
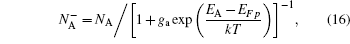
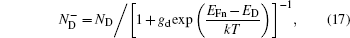
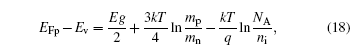



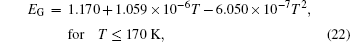

The Fermi–Dirac statistics is necessary for 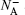
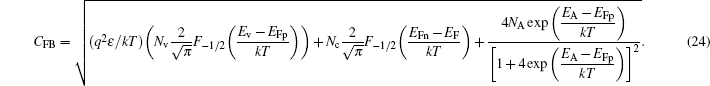
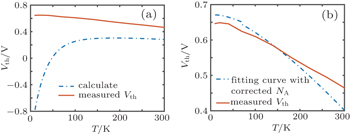
As is well known, Vth is defined as the gate voltage when the surface potential Ψs is equal to 2ΨB, where ΨB is the Fermi potential of bulk. In this paper, threshold voltage is determined from the device turn-on characteristic in the linear region. For NMOSFET, threshold voltage is defined as
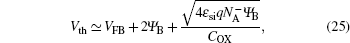

Furthermore in Eq. (
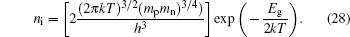
The cryogenic characteristics of H-gate SOI MOS fabricated with 0.18-μm PDSOI process are presented in this paper. Both of the important I–V and C–V parameter variations with temperature from 300 K to 10 K are discussed. We observe an obvious decrease in sub-threshold swing S and increase in transconductance Gm at cryogenic temperature. As temperature decreases, the decrease of series resistance exerts a huge impact on the test of oxide capacitance due to higher effective carrier mobility.
The freeze-out effect should be considered at cryogenic temperature, because it can reduce the concentration of ionized impurities which have a big influence on electrical parameters. For example, it can induce the Fermi-energy drift and narrow the energy gap, thus increasing the magnitude of flatband voltage and further increasing threshold voltage Vth. As a result, the current of MOS will be changed.
Furthermore, the comparison of different structures (traditional straight-gate and H-gate) will be done in later work. The significant I–V and C–V performance of SOI MOSFETs at cryogenic temperature provides an immense potential in the deep space application.
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 | |
| 18 | |
| 19 | |
| 20 | |
| 21 | |
| 22 | |
| 23 | |
| 24 | |
| 25 | |
| 26 | |
| 27 | |
| 28 | |
| 29 | |
| 30 |