† Corresponding author. E-mail:
Project supported by the Major Program of the National Natural Science Foundation of China (Grant Nos. 61790583, 61874043, 61874045, and 61775060) and the National Key Research and Development Program, China (Grant No. 2016YFB0501604).
Narrow-gap Hg1−xCdxTe material with a composition x of about 0.3 plays an extremely important role in mid-infrared detection applications. In this work, the optical properties of doped HgCdTe with x ≈ 0.3 are reviewed, including the defects and defect levels of intrinsic VHg and the extrinsic amphoteric arsenic (As) dopants, which can act as shallow/deep donors and acceptors. The influence of the defects on the determination of band-edge electronic structure is discussed when absorption or photoluminescence spectra are considered. The inconsistency between these two optical techniques is demonstrated and analyzed by taking into account the Fermi level position as a function of composition, doping level, conductivity type, and temperature. The defect level and its evolution, especially in As-doped HgCdTe, are presented. Our results provide a systematic understanding of the mechanisms and help for optimizing annealing conditions towards p-type As-activation, and eventually for fabricating high performance mid-infrared detectors.
The importance of the variable band gap Hg1−xCdxTe semiconductors for infrared detection is well known; e.g., the small composition HgCdTe material with x ≤ 0.3 still plays an extremely important role in fabricating mid-infrared focal plane arrays or multi-color detectors and may keep this status in the future.[1,2] For high-quality HgCdTe devices, the realization of p-type doping (or conductivity) is vital and has received much attention during the past few decades.[3,4] A direct and straight forward technique in which intrinsic p-type conductivity is realized by the cation metal vacancy VHg-doping as shallow acceptors is the most desirable. This is implemented during the growth of bulk material or by liquid phase epitaxy (LPE). However, VHg is also known to act as Shockley–Read–Hall recombination centers for minority carriers, thus shortening the carrier lifetime and reducing the quantum efficiency of detectors with p-type photon absorption layers. This, on the one hand, limits the effective p-type carrier density (typically below ∼1018 cm−3) and, on the other hand, degrades the crystal quality if the p-type conductivity level rises by increasing the intrinsic cation vacancy concentration.
In this case, the p-type conductivity implemented by extrinsic p-type doping in HgCdTe becomes more and more favorable and has been extensively investigated with the goal of fabricating large scale high performance infrared detector focal plane arrays. Until to now, the column V elemental arsenic (As) is thought as the most favorite dopant, mainly because of its stability and low diffusivity in HgCdTe, which is related to the best device performance parameters.[5,6] Another important advantage is involved in the growth method of in situ As-doping in HgCdTe by the molecular beam epitaxy (MBE), which can avoid high Hg pressures and lattice imperfections.[7] However, the As dopant in HgCdTe is electrically amphoteric. Under metal-rich condition it can be incorporated as an acceptor as AsTe (As occupies the Te site), while it is incorporated as a donor as AsHg (As occupies the Hg site) under Te-rich growth condition.[7,8] Thereafter, a post-growth annealing process, especially a two-stage annealing process, has been proposed to realize extrinsic p-type conductivity. This takes place by transferring the As from occupying Hg-sublattice sites to Te-sublattice sites under low activation temperature (e.g., < 300 °C) for preserving the intrinsic advantages of the low growth temperature of MBE. Different activation annealing processes on As-doped HgCdTe have been investigated by using different growth technologies, theoretical calculations, electrical measurements, and optical methods such as in our previous researches by modulating photoluminescence (PL) and photoreflectance (PR).[9–11] However, it is difficult to reach a consistent result on: (i) the optimized annealing condition, (ii) the physical mechanism relating to a low activation temperature, (iii) the defect activation energies, and (iv) the origin of As when GaAs is employed as the substrate.
Precise knowledge about the key parameters (such as the optical bandgap Eg) of doped-HgCdTe is a prerequisite for developing high quality devices. To obtain the most important optical bandgap value Eg of the materials, intrinsic absorption and transmission spectra are frequently analyzed, usually at a temperature of 77 K (liquid nitrogen temperature) or 300 K (room-temperature);[12] or for devices, the cutoff wavelength obtained from photocurrent (PC) spectra at room temperature is analyzed. Accordingly, the composition (x) can be deduced by using empirical formulas, e.g., CXT by Chu et al.[13] or HSC by Hansen et al.,[14] which work for a given sample if Eg changes linearly with temperature. Experimentally, the intrinsic absorption spectrum is determined by Fourier transform infrared (FTIR) spectroscopy that is regarded as a classical, straightforward, and accurate way to evaluate the optical Eg of HgCdTe. In such measurements, a non-linear shift of the absorption edge was observed with temperature in all kinds of doped HgCdTe, including material intrinsically or extrinsically doping. This suggests that the defects in HgCdTe influence the absorption edge and an extrinsic absorption edge is generated by contributions of defect-related transitions. This subsequently affects the determination of Eg (as well as the x value) of HgCdTe.
As mentioned previously, PL spectroscopy provides an effective way to investigate the band-edge electronic structure of doped-HgCdTe including the so-called PL bandgap (

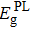
In this work, we review the optical properties of VHg- or As-doped HgCdTe with x ∼ 0.3, grown by different methods including bulk growth, LPE, and MBE. Absorption and PL spectra at different temperatures are used to analyze the optical bandgaps (Eg and 
The samples used in this work include VHg-doped HgCdTe grown as bulk material, by LPE and MBE, and As-doped HgCdTe grown by MBE. For As-activation, different annealing conditions have been used. The main composition of the samples is x ∼ 0.3.
The infrared reflectance, absorption, and PL were measured. Variable temperatures (from ∼ 8 K to 300 K) were used for absorption and PL measurements. For PL, different excitation densities were applied. As a reference, PC and photo-reflectance (PR) results have been used.
Bulk HgCdTe samples were prepared by the Bridgman method. The p-type conductivity is due to intrinsic VHg, leading to a carrier density on the order of 1014 cm−3 at 77 K. The corresponding carrier mobility was on the order of 104 cm2/V·s. The thickness of the samples was determined by a micrometer gauge with a standard thickness of less than 500 μm.
The LPE samples were VHg-doped by using a reflux vertical impregnation LPE system, which allows to grow big-area, compositional uniform, good surface profile epilayers with a controllable pressure of the solution. The substrates of the epilayers were (111) surfaces of CdTe or CdZnTe (∼ 4% of Zn), the latter was for the purpose of lattice match. The surface area was about 18 mm × 20 mm. The substrate was fixed by a clamp with a vertical inlet and outlet way. In a horizontal growth process, both the drop and pull-up of the sample were in vertical direction, while the growth direction was horizontal. The horizontal growth made the composition and thickness of the epitaxial layer uniform, while the vertical separation from the growth solution reduced the adhesion of any mother solution. After growth, the samples were annealed at different temperatures and times under Hg-rich condition. The p-type conductivity at 77 K was due to VHg, leading to a carrier density on the order of 1015 cm−3. The LPE samples L1–L6 were used for analysis. Among them, the main differences were the x value, the thickness, and, of course, the carrier density and mobility. The thickness of the HgCdTe layer was evaluated based on the Fabry–Pérot interference in the transmission spectra and was typically 10 μm.
The MBE-grown HgCdTe epilayers were grown in a Riber 32P MBE system on undoped semi-insulating GaAs (211)B substrates. A CdTe buffer layer 3 μm in thickness was grown prior to the HgCdTe nucleation. For comparison, As-doped and VHg-doped MBE samples were prepared. Except for the as-grown reference epilayer without any annealing, the other samples were annealed including a single- or two-stage annealing process, where the latter (e.g., 285 °C/0.5 h + 240 °C/48 h) was known to be beneficial to the As-activation without other residents. This happens because the first stage pushes the As from Hg sites to Te sites and the second stage, with a relatively low temperature, can remove the excess VHg and avoid forming the n-type AsHg.[17,18] The details of the samples are listed in Table
| Table 1. Composition (x), thickness (d), carrier density (Nc), mobility (Mc), and nature of defects in MBE samples. . |
Characterization by optical absorption was performed by using a Bruker IFS 66v/S spectrometer, which was equipped with a KBr beam splitter and a liquid-nitrogen-cooled HgCdTe detector. The spectrometer was evacuated during the measurement to avoid any influence of infrared absorption lines in air.
PL spectra were recorded with this setup by using the step-scan option of the FTIR as described elsewhere in detail.[15] The 514.5 nm line of a mechanically chopped (1.8 KHz) Ar+ laser was used to irradiate the sample with a beam diameter of ∼ 200 μm.
Before the experiment, the samples were treated with a quick etch in a 1% Br2/methanol solution to avoid influencing the surface smear, and then mounted on the cold finger of an Oxford closed-cycle cryostat. The temperature was adjusted from ∼8 K to 300 K. The spectral resolution was set to be 6 cm−1 or 0.7 meV.
Figures
According to the transmission spectra at any temperature, one can obtain the optical Eg value of HgCdTe. However, when the sample is doped, it can be imagined that the defects can be activated thermally and the carrier density is determined by the doping level and the temperature. This suggests that the absorption process of the carriers in the doped samples should be different from that without doping, on which transmission measurements are often considered to provide the intrinsic absorption spectra.
Figure
From the transmission spectra given in Figs.
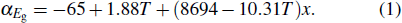 |
 | Fig. 3. Absorption coefficient spectra of (a) bulk, (b) LPE, and (c) MBE samples at different temperatures. |
Because of the difference in α values between the bulk and epilayer due to the thickness difference of HgCdTe, different procedures should be undertaken for these two kinds of samples in order to determine the critical point on the absorption spectrum. For the bulk samples with a thickness on the order of submillimeters, the absorption coefficient is extrapolated to the αEg as the critical point (Fig.
Figure
 |
The consistent x value can be calculated by referring to the absorption coefficient spectra at any temperature point and Eq. (
As shown in Fig.
Figure
PL measurements have been performed at different excitation power and temperatures. Figure
 | Fig. 6. (a), (b) Excitation power and (c) temperature dependence of the fit parameters obtained from the PL spectra. |
Figure 
Now we come to the As-doped samples, which are grown by MBE. Figure
 | Fig. 7. Representative PL spectra of (a) as-grown sample M0 and (b) As-activated annealed sample M2 at ∼ 8 K, and their line-shape fits. The samples are grown by MBE. |
Figure 
 | Fig. 8. PL spectra of sample M2 at different excitation powers and temperatures, and (c), (d) excitation power- and (b) temperature-dependent peak energy and peak integral intensity. |
To find an optimized annealing process, different annealing procedures are tested. Figure
 | Fig. 9. (a), (b) PL spectra of an As-doped MBE sample (M1) treated with a single-stage annealing process; (c), (d) the peak energies at different excitation powers and temperatures. |
After obtaining the specific defect information, the discussion of the origin of abundant peaks in the as-grown sample becomes easier. Figure
 | Fig. 10. (a) PL spectra of sample M0 and (b) temperature dependence of the peak energy. For the sake of clarity, the values of F and G in panel (b) are upshifted by 35 meV. |
Figure
It is obvious that the high energy peaks A–D (maybe E, as well) show a parabolic evolution at low temperatures but as the temperature increases beyond 20 K, they evolve in a linear increase way. The deep-level-related peaks F–H shift linearly with temperature increasing. The peak positions of A–H can be determined by extrapolating to 0 K as ∼ 238 meV, 232 meV, 225 meV, 221 meV, 207 meV, 164 meV, 146 meV, and 180 meV, respectively. Obviously, peak A has the characteristics of band-to-band transitions, while peaks B–H are related to defect-related transitions. According to the energy separation of these peaks and the statements given above, the high energy peaks B–E can be attributed to AsHg (∼ 6 meV), VHg (∼ 13 meV), TeHg (∼ 17 meV), and the AsHg–VHg complex (∼ 31 meV) transitions, respectively. Note that (i) in the unintentionally-doped or the annealed As-doped samples, none of deep levels like peaks F–H is observed; and (ii) peak H only appears at high temperatures and almost overlaps the evolution of peak G in the temperature range after the upshift of 35 meV of peak G. These may suggest that (i) peaks F–H should be related to the As dopant, such as the As-related cluster (or perhaps its complex with VHg) due to the dopant source of As4, which is prone to form Asi (i = 1, 2, and 4) clusters or interstitials in as-grown even by using a thermal cracker cell; and (ii) the deep levels are totally dependent on temperature, showing that the increase can first make the peak G-related defect state dissociate and strengthen the intensities of peaks F and H, and then make the peak F-related defect state de-complicated (to the H-related defect state) as the temperature increases further. However, obviously, the annealing process can annihilate all of them fully.[11,19]
The band-edge electronic structure in As-doped HgCdTe is schematically summarized in Fig.
As mentioned above, we observe that the absorption edge shifts abnormally with temperature increasing, and the determined Eg is inconsistent with the direct PL result 


 | Fig. 12. (a) Comparison between PL and absorption spectra of a representative LPE sample, (b)–(e) plots of temperature-dependent optical bandgap value obtained from absorption and PL spectra, and experimental Stokes shifts.[36] For comparison, the Stokes shifts are also shown according to the CXT formula. |
Details are shown in Figs. 


Based on this discussion, it can be imagined that to accurately determine the optical bandgap Eg (on which the x value depends in HgCdTe) is a key issue, because the measurement temperature point plays a vital role for different spectroscopic techniques including the transmission and PL. It involves that the reference temperature is intrinsically dependent on the selected optical method. Thus, to evaluate the accuracy of the determination of the optical Eg, figure
From this figure, we can see that if the cutoff wavelength (or energy) of the PC spectrum is considered as the value of Eg for the material, the PR spectrum, which can give the fine electronic structure including the defect levels also gives a very consistent value. However, this value is a little blue-shifted as compared with the PL results but a little red-shifted as compared with the transmission results, and this value is used as a standard value to evaluate the optical Eg of semiconductors, where the Stokes shift has a positive coefficient. Note that the PL spectrum at 77 K does not show the defect-related (i.e., VHg) emission peak, while at a low temperature (10 K), the VHg-related peak is evident as shown by the first sample (Fig.
The Stokes shift Es exists between the absorption and PL spectra, which are based on the reverse transition process of carriers. Thus, to explain the non-monotonic shift of the absorption edge and subsequently the abnormal shift of Es as temperature increases, it is vital to determine the position of the Fermi level EF, which influences the probability of transitions in a certain state. The electrical neutrality condition can be written as follows when considering p-type HgCdTe with only one single acceptor:
 |
 |
 |
For comparison with the ionized defects, we calculate the intrinsic density of carriers ni according to[23]
 |
In the temperature range of the non-monotonic shift of the absorption edge, equation (
 |
 |
 |
 |
 |
 |
The EF is a function of x, conductivity type, doping level, and ionization energy of defect. We mainly focus on the doping levels from 1014 to 1017 cm3 by considering the general density of extrinsic and intrinsic dopants in HgCdTe.[38–40] Figure
Table
| Table 2. Calculated values of the specified temperature points described in EF function. . |
According to the EF ∼ T expression and the experimental data, the temperature-dependent transitions can be explained when extrinsic/intrinsic shallow levels exist in HgCdTe, independent of growth methods and conductivity types, as well as dopant sources. As the experimental observation and the calculated result, the values of Td and Te represent the critical points of the non-monotonic shift of the absorption edge, the former corresponding to the occurrence of defect-related transition contribution and the latter for the full contribution of the defect-related transition.
Thus, a schematic evolution of the carrier transition can be presented by taking a p-type Hg0.7Cd.3Te for example as shown in Fig.
Intrinsic VHg doping provides a way to realize p-type HgCdTe, although the carrier density and the mobility are limited. The extrinsic-As doping presents an option for high quality epilayers but specified annealing processes are necessary, such as a two-stage process with a relatively low temperature of 285 °C to activate the As to occupy Te sites and simultaneously to avoid producing the excessive VHg. Optical characterization by utilizing transmission and PL spectroscopy can optimize the annealing conditions through analyzing the defects generated or eliminated in different annealing processes. After the value of Eg in HgCdTe is determined, the transmission can effectively disclose the band-to-band transition of carriers, but the reference temperature is a main factor in the measurement. This is because defects in HgCdTe can influence the contribution of the band-related carrier transition to the intrinsic absorption edge, which on one hand leads to a non-monotonic shift of the absorption edge energy with temperature increasing in the low temperature range < 100 K, and on the other hand makes the experimental Stokes energy abnormally shift from positive to negative when the temperature is beyond the critical point or the corresponding defect activation energy.
To evaluate the optical Eg of the doped HgCdTe, the absorption should be measured at very low temperatures; e.g., far below 77 K. While for the PL measurement, a much high temperature–e.g., up to ambient temperature–is beneficial to avoid the influence from the defects or the band tail states. The lower activation energy of the As (denoted as AsTe) than VHg points to the advantages of fabricating p-type HgCdTe-devices based on the As-doped HgCdTe after the application of a suitable annealing process.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] | |
| [39] | |
| [40] |











