† Corresponding author. E-mail:
Project supported by the Research Program of the National University of Defense Technology (Grant No. JC 13-06-04).
In this paper, the three-dimensional (3D) coupling effect is discussed for nanowire junctionless silicon-on-insulator (SOI) FinFETs. With fin width decreasing from 100 nm to 7 nm, the electric field induced by the lateral gates increases and therefore the influence of back gate on the threshold voltage weakens. For a narrow and tall fin, the lateral gates mainly control the channel and therefore the effect of back gate decreases. A simple two-dimensional (2D) potential model is proposed for the subthreshold region of junctionless SOI FinFET. TCAD simulations validate our model. It can be used to extract the threshold voltage and doping concentration. In addition, the tuning of back gate on the threshold voltage can be predicted.
Since their invention by J-P. Colinge, junctionless (JL) transistors have been a compelling candidate for ultra-scaled devices due to their excellent electrostatic gate control and simplified junction engineering.[1] These transistors have shown the promising applications in the field of analog/RF,[2] logic[3] and sensing circuits.[4] JL MOSFETs are usually designed with heavily doped silicon films (∼ 1019 cm−3) in order to achieve enough drain current. Owing to the high doping concentration of the channel, the carrier transport in a JL transistor relies on volume conduction instead of the conventional surface inversion in MOSFET. This device is switched off by fully depleting its heavily doped channel. Thus, the geometry of the channel must be small enough to permit the full depletion at a desired gate voltage. The junctionless transistor can operate in three modes: full depletion, partial depletion, and surface accumulation. The threshold voltage and flat-band voltage are the key identifiers to distinguish the three modes.
In classical inversion-mode FD SOI MOSFET, the operation of the transistor is governed by both front and back channels. This phenomenon is well known as the coupling effect between front and back gates, which has been demonstrated to have a strong influence on the threshold voltage and mobility.[5–7] However, most studies of the coupling effect involve the inversion-mode SOI MOSFETs with undoped or low-doped channel. There are few reports on the coupling effect in the JL transistor with a heavily doped channel. Owing to the small cross-section of the channel in the JL transistor, the coupling effect is expected to happen as in the inversion-mode SOI MOSFETs.[8,9]
On the other hand, the junctionless SOI FinFET with multiple gates has been fabricated due to its novel performance.[10,11] In the JL SOI FinFET, we must consider the effect of the lateral electric field between the two lateral gates. This lateral electric field which makes the difference between planar and FinFETs enhances the coupling effect. The enhanced coupling effect will lead to the difficulties in determining the threshold voltage, which reflects the full depletion of the doped channel. Several models based on the approximate solution of the Poisson equation have been proposed: a one-dimensional (1D) model for double-gate JL devices,[12–14] a 1D potential model in the full depletion region for double-gate JL transistors,[15] a 2D surface-potential-based current model for triple-gate transistors,[16] etc. While 2D models are too complicated to be used for parameter extraction, a 1D model does not consider the coupling effect between the gates.[17] Therefore, a simple model including the coupling effect between gates is imperative for parameter extraction in JL SOI FinFET.
In this paper, we will take the coupling effect into account in the modeling of JL SOI FinFET. We focus on the modeling of potential and the coupling effect in the subthreshold region (depletion region for JL transistor). Section 2 will show the evidence of coupling effects in JL SOI FinFETs. In Section 3, we will propose a 2D model for potential distribution in a subthreshold region. TCAD simulations are performed to validate our model. Based on this model, a simple and fast method to determine the threshold voltage is developed by considering the coupling effects, which will be explained in Section 4. In Section 5 we will draw some conclusions from the present study.
Before the 2D analytical model with considering the coupling effect in JL SOI FinFETs, we will firstly show the simulated characteristics of JL SOI FinFETs. The coupling effects will be uncovered by comparing the influences of fin width, film thickness and backgate on the characteristic curves.
Figure
Synopsys Sentaurus TCAD is employed for all simulations.[19] Fermi-Dirac distribution is employed due to the heavily doped channel. The effect of doping, velocity saturation and the surface scattering are considered. The Shockley–Read–Hall recombination dependent on the doping level and Auger recombination are also included. The work-functions of the front and back gates are selected to make the flat-band voltages (VFBF and VFBB) equal zero. Both the front- and the back-gate leakages are neglected.[18] The drain is 0.05 V and the gate is swept from −1.5 V to +1.5 V. All the simulations are 3D simulations.
Figure
 | Fig. 2. (a) Simulated drain currents and (b) transconductance versus front gate voltage for wide JL SOI FinFETs. ND = 1019 cm−3, Tsi = 9 nm, VD = 0.05 V, and VBG = 0 V. |
These modes of operation are also reflected by the contours of electron density in Fig. accumulation mode (VFG > VFBF), in which the drain current is the sum of volume current and accumulation current (Fig. partial depletion mode, in which the drain current comes from the volume conduction in the undepleted region (Fig. full depletion mode, in which the drain current decreases sharply with VFG (Fig.
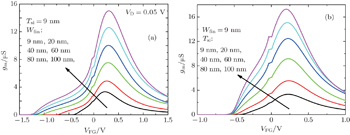
The effect of fin width on the transconductance curves gm(VFG) is shown in Fig.
Figure
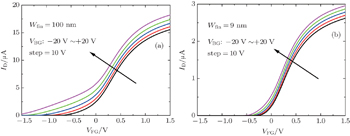 | Fig. 5. Effects of back gate on the drain currents for (a) wide and (b) narrow JL SOI FinFETs. ND = 1019 cm−3, Tsi = 9 nm, and VD = 0.05 V. |
This suppression of coupling effect between top and back gates is also visible in the comparison among gm(VFG) curves under different back gate biases (Fig.
 | Fig. 6. Effects of back gate on the transconductance for (a) wide and (b) narrow JL SOI FinFETs. ND = 1019 cm−3, Tsi = 9 nm, and VD = 0.05 V. |
In summary, the coupling effect in JL SOI FinFET plays the same role as in the inversion-mode vertical DG SOI FinFET[9]
In the 2D analytical model of triple-gate SOI FinFETs proposed by Akarvardar et al.,[22] a parabolic potential variation between the two lateral gates is assumed. Here, we still assume that the potential profile between the two lateral gates is parabolic in the JL SOI FinFETs:

The coefficients of Eq. (
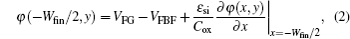

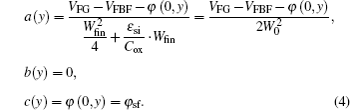

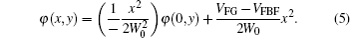

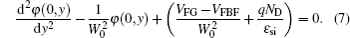
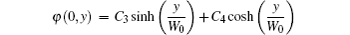



Substituting Eq. (






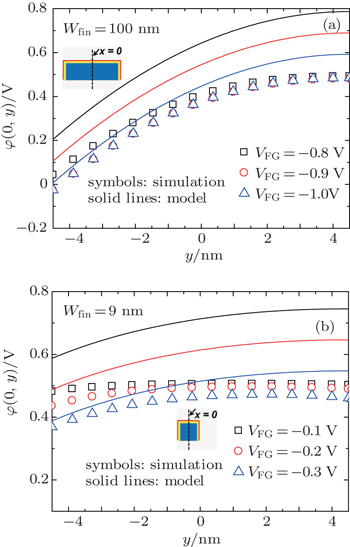
In order to validate our model for the potential distribution in JL SOI FinFET, we make a comparison of φ(0,y), the potential of the full depletion region along x = 0 (vertically cut in the middle of the channel, see Fig.
However, in the partial depletion region, the modeled potentials deviate from the simulated ones as shown in Fig.
The effects of back gate on the potential in both wide and narrow JL SOI FinFETs are shown in Fig.
In summary, this 2D potential model works in the full depletion regime with zero back gate bias or with VBG < 0 V (depletion at back interface).
Since our 2D potential model successfully applies to the full depletion region of nano-channel JL SOI FinFET, we can use it to extract the threshold voltage, which is a key identifier to distinguish the full and partial depletion regions. Before using the model, we will introduce the current-voltage method proposed by Jeon et al.[23] to extract threshold voltage.
In a planar junctionless transistor, the threshold voltage is determined from the derivative of the transconductance (dgm/dVFG), shown in Fig.
According to Ref. [15], the threshold voltage VTHF for a junctionless transistor can be defined as the front gate voltage when the channel is just fully depleted. It is given as the maximum potential at (x, y) = (0, −Tsi/2) for VBG = 0 V from Eq. (


For depletion in the back channel, the point ym depleted finally lies in the middle of the channel along x = 0. Assume that the potential at ym does not vary with VFG nor VBG and is always equal to the Fermi potential φF, we have



 | Fig. 13. Plots of (a) ym versus VBG, and (b) comparisons of extracted VTHF between the dgm/dVFG method and our model (Eq. ( |
It follows that equation (
Once the threshold voltage and flat-band voltage are known, the doping concentration of the channel can be determined. We can rewrite Eq. (

| Table 1. Extracted doping level from Eq. ( |
In this paper, we prove the coupling effects for JL SOI FinFETs and propose a simple analytical model to determine the 2D potential profile within the body. The very good agreement obtained between simulated and modeling results validates the model. It works well in the full depletion region. The proposed models can be used for analysis of the coupling effect, characterization and optimization of geometry in any other heavily doped FinFETs. On the other hand, understanding these coupling effects and modeling them accurately are of great importance for applications. For example, increasing threshold voltage can reduce leakage current and power consumption. Conversely, lower operating bias is achieved with reduced threshold voltage. Also, we can co-integrate different functions into the same chip by tuning the threshold voltage.
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 | |
| 18 | |
| 19 | |
| 20 | |
| 21 | |
| 22 | |
| 23 |