† Corresponding author. E-mail:
The electrical characteristics of a double-gate armchair silicene nanoribbon field-effect-transistor (DG ASiNR FET) are thoroughly investigated by using a ballistic quantum transport model based on non-equilibrium Green’s function (NEGF) approach self-consistently coupled with a three-dimensional (3D) Poisson equation. We evaluate the influence of variation in uniaxial tensile strain, ribbon temperature and oxide thickness on the on-off current ratio, subthreshold swing, transconductance and the delay time of a 12-nm-length ultranarrow ASiNR FET. A novel two-parameter strain magnitude and temperature-dependent model is presented for designing an optimized device possessing balanced amelioration of all the electrical parameters. We demonstrate that employing HfO 2 as the gate insulator can be a favorable choice and simultaneous use of it with proper combination of temperature and strain magnitude can achieve better device performance. Furthermore, a general model power (GMP) is derived which explicitly provides the electron effective mass as a function of the bandgap of a hydrogen passivated ASiNR under strain.
The monolayer honeycomb structure of silicon, silicene, [ 1 ] has appeared as an attractive one-atom thick material that might be highly compatible with the current silicon nanoelectronic technology. Similar to graphene, [ 2 ] silicene is also a gapless semimetal with linearly crossing bands near the Fermi level. Carriers in a silicene sheet are projected to face massless behavior in the vicinity of the Dirac point that would lead to a quite large mobility. Silicene stabilizes to form an unprecedented low-buckled (LB) geometry. [ 3 ] The height difference between the two nearest neighboring atoms in silicene, provides a tunable bandgap and makes this silicon allotrope a good candidate for switching and modulation applications. Exhibiting many characteristics of topological-insulators, [ 4 ] a quantum spin Hall effect [ 5 ] and attractive optoelectronic properties [ 6 ] are some of the distinguished aspects of silicene. Beside the aforementioned properties, high mechanical strength and elasticity [ 7 , 8 ] and low temperature synthesis, [ 9 ] altogether facilitate the conditions for the integration of silicene-based devices.
Scaling down the channel length of the field-effect-transistor (FET) makes the device suffer from short channel effects. [ 10 ] In order to enable continued FET scaling, an alternative channel geometry/material can be employed. Among the different classes of channel materials under study, the two-dimensional (2D) material silicene is of great importance due to the fact that it would be easier to adjust next-generation FETs to the silicene process technology. Meanwhile, the single layer material provides extremely good gate control over the channel. In this sense, silicene-based FETs are expected to greatly suppress short channel effects and provide better scalability of the device. Most recent, encapsulated silicene FET fabrication provided the first proof of concept for the silicene devices. Nevertheless, research on the application of silicene nanoribbons as the channel material of FETs is in their infancy and requires more comprehensive investigations. [ 9 ]
According to the International Technology Roadmap for Semiconductors (ITRS), [ 11 ] at 12-nm technology node where current FETs reach their physical scaling limits, [ 12 ] for silicene-based FETs to be an ideal alternative, a minimum gap of about 0.4 eV is required. A suitable bandgap for electronic applications can be achieved by patterning silicene into a narrow ribbon. [ 13 ] Independent of different shapes of the ribbon, armchair silicene nanoribbon (ASiNR) with 4 dimer lines along the width, 4-ASiNR, has great potential to be used in the electronics due to its large transport bandgap. In this paper, main electrical parameters of 4-ASiNR double-gate (DG) FET which play an important role in assessing the performance of the transistor, i.e., on–off current ratio, subthreshold swing, on-state saturation current, transconductance, and the delay time are calculated under different physical constraints and varying design parameters including the ribbon temperature, gate insulator thickness/material and uniaxial tensile strain. A new model is also proposed which determines appropriate values of temperature and strain to pave the way for designing a device with optimized performance suitable for digital and analog applications.
The ab initio study of quantum transport, [ 14 ] semiclassical top-of-the-barrier [ 15 ] and analytical electrical transport [ 16 ] are the three theoretical models that have been explored for the silicene-based FETs. However, a 3D coupled Poisson-quantum transport model to accurately evaluate the electrical characteristics of a DG silicene FET has not been explored yet. In this paper, numerical simulations are carried out based on the self-consistent solution of the 3D Poisson and Schrödinger equations, within the non-equilibrium Green’s function (NEGF) formalism, [ 17 ] implemented in NANOTCAD ViDES simulator. [ 18 , 19 ] The nearest-neighbor tight-binding (TB) Hamiltonian is expressed on a p z orbital basis set in the real-space. [ 20 ]
The rest of this paper is organized as follows: Section 2 discusses the band structure calculation of the unstrained and uniaxially tensile strained ASiNR, where an analytical formula is derived for the effective mass as a function of bandgap of the ribbon and the strain. Next, it elucidates the quantum transport of DG ASiNR FET within NEGF approach. In Section 3, the influence of physical and structural parameters on the electrical characteristics of 4-ASiNR FET is investigated. The method for designing a device with balanced electrical parameters is thoroughly presented in Section 4. In Section 5, we provide a summary.
The schematics of the device under study and the potential profile along the channel are presented in Fig.
 | Fig. 1. Schematics cross-section of (top) the simulated DG FET with the intrinsic 4-ASiNR as the channel material and (bottom) the self-consistent electrostatic potential profile along the device. |
We have employed TB approach for computing the energy bandgap of ASiNRs as a function of the ribbon’s width shown in Fig.
 | Fig. 2. (a) Energy bandgap of ASiNRs as a function of the ribbon’s width calculated by TB formalism and verified by DFT approach. (b) E − K dispersion of relaxed 4-ASiNR. |
Strain is a well-known efficient method, which modulates the electrical transport properties of a nanoscale system. This procedure has a significant influence not only on the energy bandgap but also on the effective mass. We analyze the effect of uniaxial tensile strain on the electronic properties of 4-ASiNR within a TB approach. The applied strain is limited to 5%, to ensure that we are in the elastic response regime. The Harrison’s model is utilized to modify the binding parameters for the strain calculations. [ 25 ] In the presence of strain, each binding parameter is scaled down by a dimensionless factor || l 0 / l || 2 , where l 0 and l are the unstrained and strained bond-lengths, respectively. We have calculated the energy bandgap and the electron effective mass of 4-ASiNR versus the uniaxial strain as depicted in Fig.

We present a general model power (GMP) to access an explicit relation between the electron effective mass and the bandgap value of ASiNR under strain. The analytical formula is applicable for different indexes of ASiNR and defined as follows:


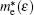
The ballistic transfer characteristic is calculated by using the NEGF formalism. [ 17 ] The retarded Green’s function of the channel, G ch , can be obtained as follows:

Once G ch is obtained, the transmission probability, T ( E ), of ASiNR FET can be evaluated for energies in the transport direction as 


The transfer characteristic of an 4-ASiNR FET is presented in Fig.
Among the important electrical parameters of ASiNR-FET, on–off current ratio and subthreshold swing are two significant parameters for low power fast switching speed applications whereas transconductance and intrinsic delay are remarkable for telecommunication usage. [ 28 , 29 ] The impact of several design parameters including temperature, uniaxial tensile strain, and gate insulator thickness on the electrical characteristics of 4-ASiNR is thoroughly investigated. The results are presented in Figs.
| Table 1. Design parameters that are employed for assessing the performance of 4-ASiNR FET, related results are depicted in Fig. |
The first figure of merit that is perceived is the on–off current ratio, Fig.
The gate capacitance of DG structure, C G , can be modeled as a series combination of the gate oxide capacitance, C ox (∝2 kε 0 / t ox ), and the quantum capacitance, C Q , which is proportional to the density of states. [ 30 ] In the off-state region, as the temperature increases, thermal energy increases the carrier concentration in the conduction band that significantly results in the channel conductance and consequently the leakage current enhancement. However, in the on-state region, C Q increases as compared with C ox which implies that the electron concentration in the conduction band exceeds the density of states. As a result, due to the high carrier concentration, the on-state current is not supposedly influenced by the temperature. Evidently, on–off current ratio degrades significantly as the temperature goes beyond 150 K. The impact of gate insulator thickness is assessed to evaluate the electrical performance of the unstrained device at room temperature. For the FETs including heavily doped contacts, the gate merely modulates the channel conductance. The increase of the gate insulator thickness induces an unreliable gate control over the channel [ 31 ] that eventually results in the increase of the subthreshold leakage current and a gentle degradation of the on–off current ratio.
Next, we focus on subthreshold swing (SS). This parameter determines how efficiently the transistor can be turned off by varying the gate source voltage, depicted in Fig.
The impact of key design parameters on the transconductance of the device under study is presented in Fig.
The final performance metric considered here is the intrinsic switching delay time. The delay time shows how fast a transistor can switch and is calculated as τ = ( Q ON – Q OFF )/ I ON , where Q ON(OFF) is the total charge in the channel in the on(off)-state. [ 36 ] Impact of strain, temperature, and gate oxide thickness on the intrinsic delay time is presented in Fig.
In this step, the effect of gate insulator material on the performance of unstrained 4-ASiNR FET is analyzed comprehensively for T = 300 K. SiO 2 ( k = 3.9), ZnO ( k = 8.5), Al 2 O 3 ( k = 9.8), ZrO 2 ( k = 20), and HfO 2 ( k = 25) are five different common insulators that are compatible with the silicon in FET technology. The on-state current dependence of the on–off current ratio and transconductance are calculated in particular and the results are depicted in Fig.
As implied in Figs.
Here, we propose a novel variation matrix, Var( m , n ), to gain insight into the effect of temperature and strain fluctuations on device performance. The objective of the variation matrix is to determine the region that provides the best combination of temperature and strain values that produces the desired balanced improvement of all the electrical parameters. First, we define the function E p ( m , n ) that denotes the effective contribution of the electrical parameters of 4-ASiNR FET to the variations of temperature and strain values. The two-parameter function is defined as follows:



The 2D variation matrix is sketched in Fig.
We have investigated the behavior of a monolayer 4-ASiNR DG FET by performing 3D self-consistent quantum transport simulations to address design considerations for obtaining a device with improved electrical performance. The effects of temperature, uniaxial tensile strain, and gate oxide thickness/material on the main electrical parameters of the ASiNR FET have been theoretically studied. Our simulation results based on NEGF formalism demonstrate that as the ribbon temperature and the strain magnitude go up, the electrical parameters of the 4-ASiNR FET have a dramatic change. The performance benefits are achieved in terms of the transconductance and intrinsic delay time, but on the other hand an increase in the subthreshold swing and a major degradation in the on–off current ratio seem challenging. However, using a thin oxide layer and high- k insulators are helpful techniques for obtaining a superior gate control over the channel and improvement of device main electrical parameters, as a consequence. Eventually, the device efficiency in terms of entire electrical parameters is improved by optimizing the related design parameters. An optimization method has been developed which provides a valuable reference for the simultaneous impact of temperature and stain magnitude on the electrical characteristics of the 4-ASiNR FET. As emphasized in this work, proper combination of temperature and strain magnitude and employing HfO 2 as the gate insulator may lead to average improvement of all the electrical parameters. We hope that this work will facilitate the research aiming at the application of silicene-based FET in nanoelectronics.
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 | |
| 18 | |
| 19 | |
| 20 | |
| 21 | |
| 22 | |
| 23 | |
| 24 | |
| 25 | |
| 26 | |
| 27 | |
| 28 | |
| 29 | |
| 30 | |
| 31 | |
| 32 | |
| 33 | |
| 34 | |
| 35 | |
| 36 | |
| 37 |







