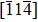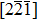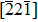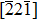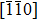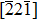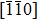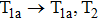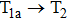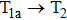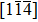† Corresponding author. E-mail:
Impurity segregation at grain boundary (GB) can significantly affect the mechanical behaviors of polycrystalline metal. The effect of nickel impurity segregated at Cu GB on the deformation mechanism relating to loading direction is comprehensively studied by atomic simulation. The atomic structures and shear responses of Cu Σ9(114) ⟨110⟩ and Σ9(221) ⟨110⟩ symmetrical tilt grain boundary with different quantities of nickel segregation are analyzed. The results show that multiple accommodative evolutions involving GB gliding, GB shear-coupling migration, and dislocation gliding can be at play, where for the 

Understanding the function of grain boundary (GB) is of great importance for regulating the properties of polycrystalline materials on a nanoscale, which suggests that the change of grain size can significantly affect the plasticity of material according to the Hall-Petch relationships.[1–4] It is well established that the GB would act as a heterogeneous nucleation source for emitting dislocations or a barrier to dislocation sliding, which would facilitate multiple deformation behaviors during external loading such as GB sliding, GB migration, local dissociation, mechanical twins, etc.[5,6] The accumulation of various defects tend to maintain a high concentration in the disordered region in GB generally.[7] Embrittlement or cohesion enhancement induced by impurity segregation at GB has been extensively analyzed.[8–13] Experimentally, impurity segregation phenomenon can be commonly investigated by transmission electron microscopy (TEM), electron backscattered diffraction (EBSD), atom probe tomography (APT) and Anger electron spectroscopy techniques.[14–16] Meanwhile, atomic scale simulation is also an essential approach to the exploration of the mechanism of how the GB segregation affects the mechanical properties of materials from energetic and electronic aspects.[17–19] According to the first-principles calculations, Lozovoi et al.[20] have determined that the embrittlement of impurity segregation is attributed to either structure effect or electronic effect in a binary copper alloy. Zhang et al.[21] further analyzed the effect of dense impurity segregation at GB on the plastic evolution of aluminum alloy. The cohesion influences of Mg, S, P segregated at tilted GB have been investigated by Li et al.,[22] indicating that chemical contribution plays a major role in GB cohesion. In Ref. [23], Chen et al. have proposed a theoretical model regarding the quasi-thermodynamics and the kinetics of non-equilibrium GB segregation and predicted the P nonequilibrium segregation induced by high temperature deformation. The recent atomic-level study reported by Zhao et al.[24] clearly showed the effects of Mg, Cu impurity segregation at GB in Al from the aspects of GB structure, charge density evolution and tensile strain. Besides, Cai et al.[25] have proved that the segregated elements could stabilize the grain size and strengthen the mechanical properties of nano-crystals experimentally.
Cu–Ni alloys have wide applications due to their high electrical resistance and low temperature coefficient.[26] Normally, Ni segregated at Cu interface or surface can hardly be observed by experimental means on account of their completely mutual miscibility and no obvious impurity-induced embrittlement effect. Nevertheless, Divinski et al.[27] proved that Ni impurity can be moderately segregated in Cu–Ni alloy, measured by the radiotracer technique. For a better understanding of segregated GB deformation mode, such an external loading is necessary to bring about plastic and fracture process.[28] Consequently, the influence of nickel enrichment at GB is well worth exploring through the combination of density functional theory (DFT) and molecular dynamic (MD) simulations. In this paper, the shear responses of Σ9(114) and Σ9(221) GB with different impurity concentrations are investigated by the MD simulations where the deformation process can be visually displayed on a large atomic scale. The DFT method is adopted to realize the accurate energetic calculations. Attention is paid to the difference among GB coupling motions with various dopants. The rest of this study is organized as follows. In Section
The original cells of CuΣ9(114)/[110] and Σ9(221)/[110] symmetric tilt GB were constructed by joining two separate (upper and lower) grains with the determinate lattice orientations. The details of models are listed in Table 

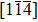

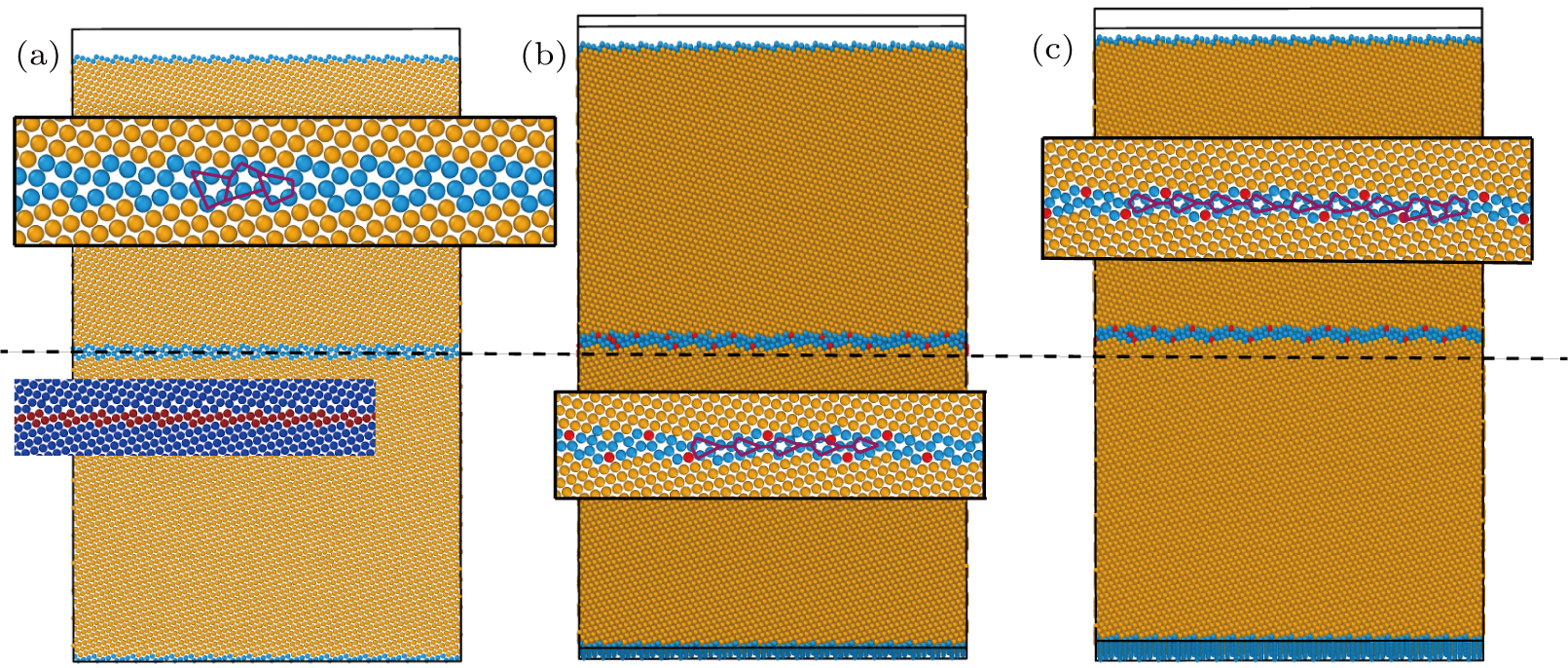
 | Fig. 1. (color online) Segregation models in MD simulations, showing impurity concentrations at high-angle GB in Cu displayed in 
|
| Table 1.
Orientation details of bicrystal cells. . |
Furthermore, to study how the concentration of GB segregated dopants affects the mechanical properties, the first-principles calculations were performed by employing VASP code.[33,34] The exchange correlation effects were described employing the generalized gradient approximation of Perdew–Burke–Ernzerhof functional (GGA-PBE).[35] A plane-wave cutoff energy of 500 eV and a suitable Gamma-centered k-point mesh were used for the geometry optimization. The global convergence criteria for electronic self-consistent cycles and interatomic force were set to be 1 × 10−5 eV and 0.01 eV/Å, respectively. Figure
The deformation response and energy calculations concerning the segregated Σ9(114) and Σ9(221) symmetric tilt GB are discussed below.
(i) Considering the overall presentation of the shear process, the stress–strain curves of pure Cu (black), Cu-0.7 at.% Ni (red), Cu-1.6 at.% Ni (green), Cu-4.3 at.% Ni (blue) model with Σ9(114)/[110] GB are plotted in Fig. 
Some typical MD snapshots are selected to display the concrete deformation processes as shown in Figs. 
The transformations of GB configuration in the four cases are approximately identical under the condition of small strain (T1a → T2, described in Fig.
(ii) As shown in Fig. 
Figures
We summarize the main mechanical behaviors of four model undergone 

| Table 2.
Dominant deformation behaviors of four Σ9(114) bicrystal models. . |
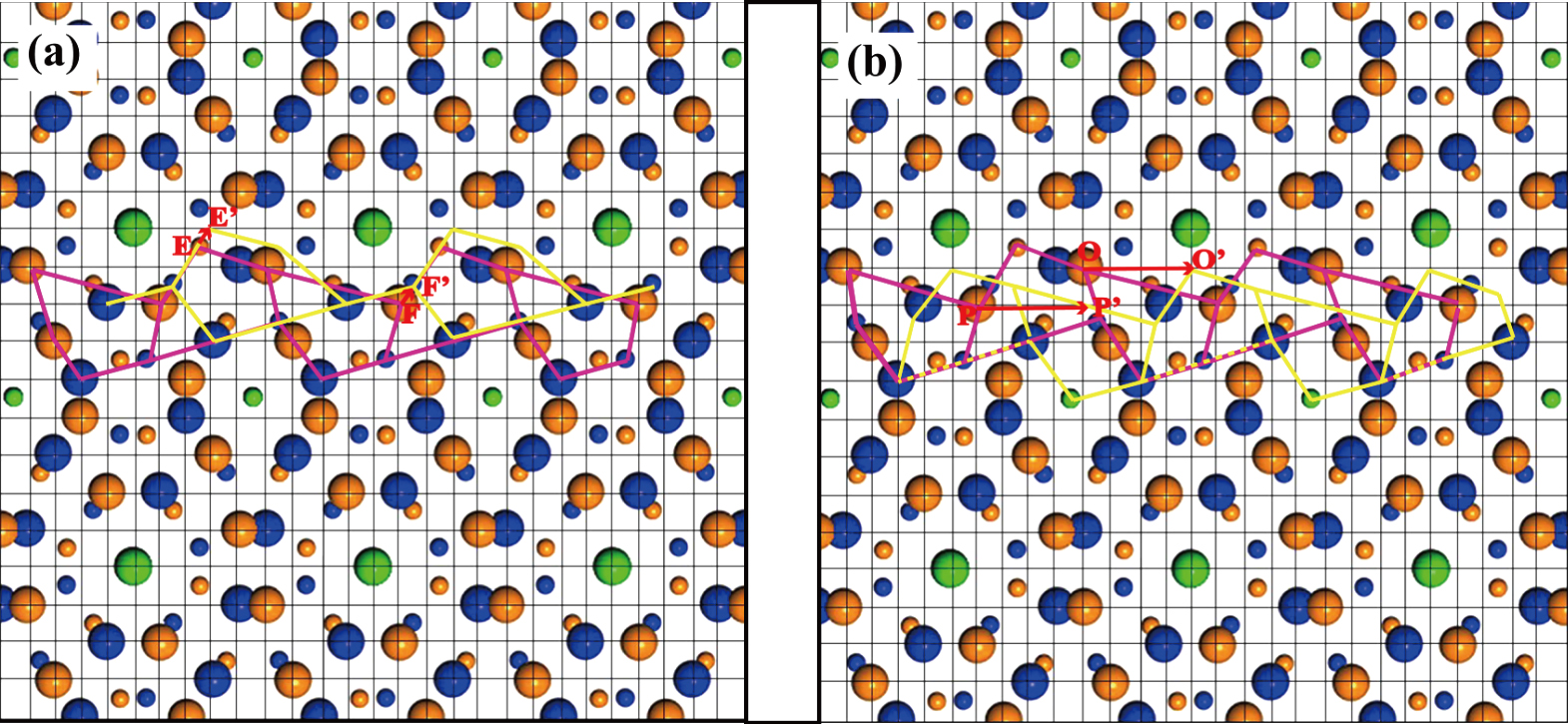
The involved structural transformations of Σ9(114) GB in the aforementioned shear processes are shown in Fig. 
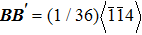

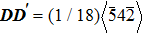
| Table 3.
Transformation processes of Σ9(114) GB structures in four bicrystal models under loading. . |
i) The stress–strain curves of pure Cu, Cu-0.7 at.% Ni, Cu-1.6 at.% Ni, Cu-4.3 at.% Ni models with Σ9(221)/[110] GB are depicted in Fig. 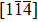
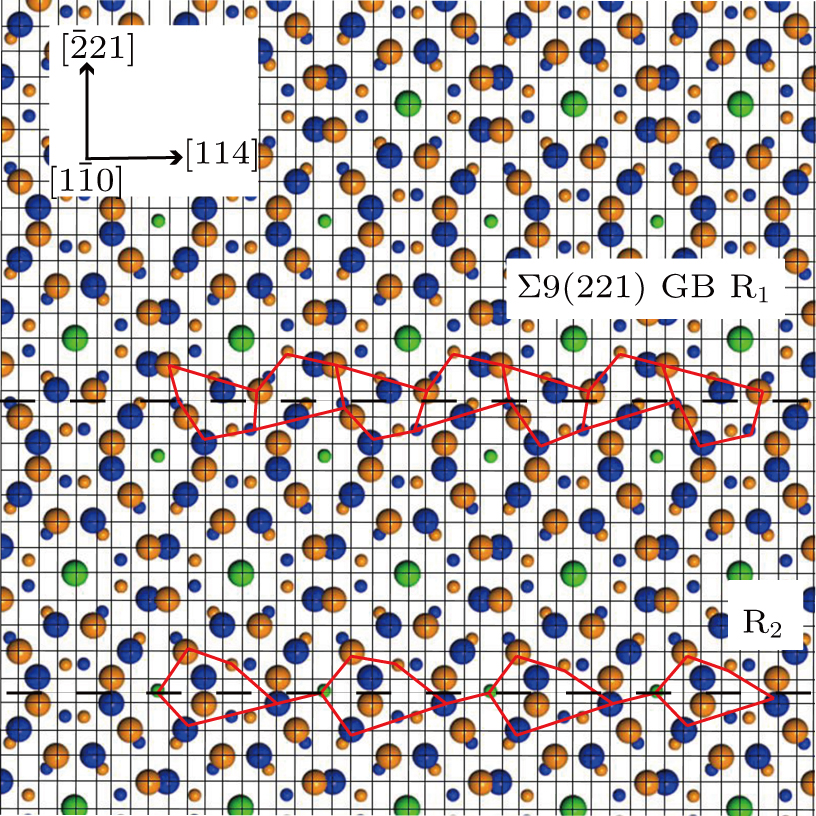
 | Fig. 14. (color online) Mechanical deformations of pure Σ9(221)/[110] Cu bi-crystal with different levels of nickel GB segregation, shearing along (a) 

|
The detailed deformation behaviors are explained in Figs.
 | Fig. 16. (color online) Atomic structures showing shear evolutions of Σ9(221) GB in Cu (Cu–Ni base) bi-crystal loading along 
|
 | Fig. 17. (color online) Atomic structures showing shear evolutions of Σ9(221) GB in Cu (Cu–Ni base) bi-crystal loading along 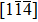
|
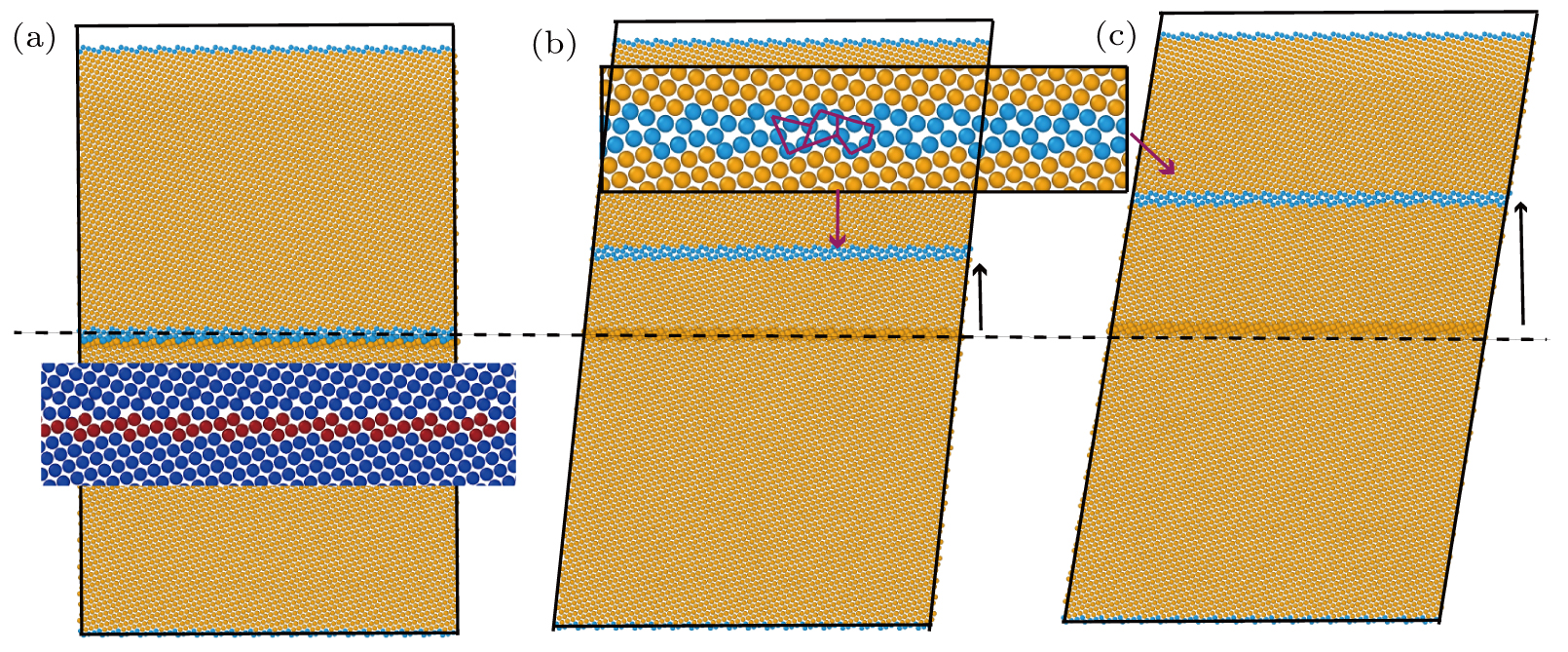 | Fig. 18. (color online) Atomic structures showing shear evolutions of Σ9(221) GB in Cu-0.7 at.% Ni bi-crystal loading along 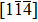
|
 | Fig. 19. (color online) Atomic structures showing shear evolutions of Σ9(221) GB in Cu-4.3 at.% Ni bi-crystal loading along 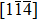
|
(ii) Figure 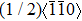
 | Fig. 21. (color online) Representative CNA snapshots of Cu-1.6 at.% Ni bi-crystal with Σ9(221) GB under shear deformation along 
|
 | Fig. 22. (color online) CNA snapshots of Cu-4.3 at.% Ni bi-crystal with Σ9(221) GB under shear deformation along 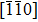
|
The deformation behaviors and the unit structure transformations in Subsection
| Table 4.
Dominant deformation behaviors of four Σ9(114) bicrystal models. . |
| Table 5.
Transformation processes of Σ9(221) GB structure in four bicrystal models under loading. . |
Figure 
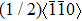
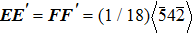



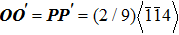
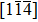
Corresponding to Subsection
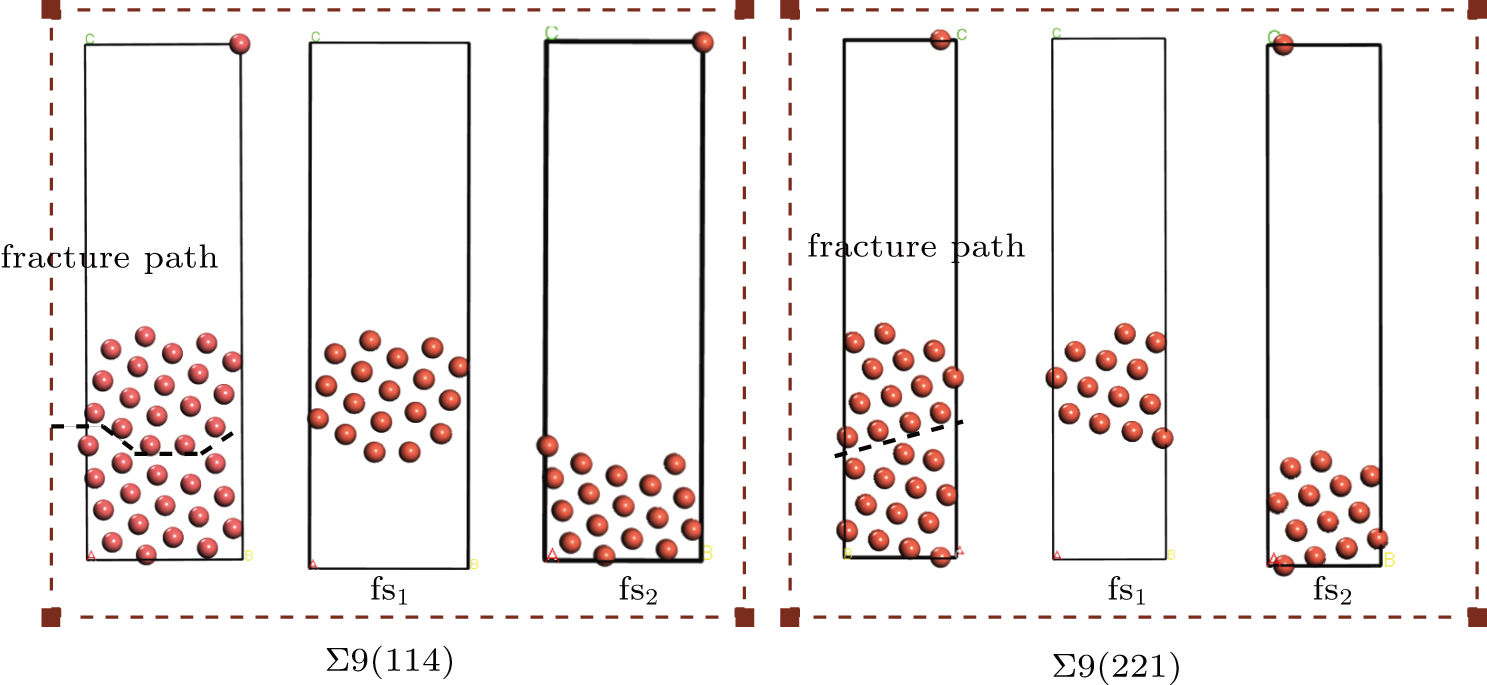 | Fig. 24. (color online) Diagrams of determined fracture paths for Σ9(114) and Σ9(221) GB models, where fs1 and fs2 represent the free surfaces caused by the fracture path. |
The calculation results are listed in Table
| Table 6.
Work of separation of Σ9(114) and Σ9(221) GB with varying segregated impurity. . |
Molecular dynamics simulations and first-principle energetic calculations have been carried out to investigate the effects of varying nickel segregation at GB on the mechanical behavior and structure configuration in copper. The deformation modes of Σ9(114) and Σ9(221) with varying segregation have been fully analyzed considering that two loading directions are parallel to GB plane. The results of this study can be summarized as follows.
The lattice dislocation activities can be motivated more commonly in models with relatively high concentration, which could improve the roughness under a high strength state. For the shear of Σ9(114) bicrystal along 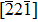

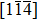

| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] |