† Corresponding author. E-mail:
We study the fractal rhythm in the ionization of Rydberg helium and lithium atoms in an electric field by using the semiclassical method. The fractal structures present a nested relationship layer by layer in the initial launch angles of the ionized electrons versus the escape time, which is defined as the rhythm attractor, and exhibit similar rhythm endings. The gradually enhanced chaotic regions of the escape time plots tend to broaden as the scaled energy increases. In addition, the fractal rhythm changes synchronously with the oscillations of the kinetic energy spectrum. We note that the intrinsic quality of the fractal rhythm is closely related to the kinetic energy distribution, that is, the inherent dynamic properties of the Hamiltonian equations have an impact on the fractal regularities. In addition, different ionizing closed trajectories exhibit iterate properties and the inherent beauty of symmetry. Our results and analysis can not only reveal new laws in the ionization of Rydberg atoms, but also promote the establishment of the dynamic mechanism of fractals.
In recent years, nonlinear science, especially chaos theory, has revealed the universality of the fractal structure in physics. Chaotic phenomena exist in many research fields, such as the escape dynamics of particles in mesoscopic devices, the ionization of high excited atoms, and so on.[1–7] The interaction between lasers and matter is an important means to explore new laws of microstructures.[8–13] The emergence and development of atomic physics in extreme strong field conditions can not only reveal new physical phenomena and effects, promote the progress of the ultra-fast laser, but also enable people to truly understand molecules, atoms, and their internal properties.[14–18]
With the advancement of laser technology and semiclassical theory, considerable attention has been paid to photoionization microscopy and the ionization dynamics of atoms in external fields.[2,6,7,19–25] The chaotic ionization of hydrogen in electric and magnetic fields is described by the Poincaré map.[26–29] Recently, with the development of chaos and fractal theory in physics, consideration has been given to fractal dynamics in many fields, for example, the fractal dynamics in quantum and semiclassical transport.[12,30–35] The escape dynamics of trapped ultracold atoms and Bose–Einstein condensates always exhibit fractal features.[36–38] What is more, diverse attractors exist in nonlinear systems, such as the limit cycle attractor, torus attractor, Lorenz attractor, strange attractor, and so on, which all reflect the diversity of the nature and the flexuosity in the process of evolution. The ionization of Rydberg atoms is one of the most interesting fields in chaos and fractal physics. It is notable that, for the ionization of multi-electron Rydberg atoms in external fields, the intrinsic quality of fractal remains unrealized. Hence, it is a challenge to find the correspondence between the fractal mechanism and the chaotic escape laws of electrons in ionization systems.
In the present paper, we study the intrinsic quality of the fractal in the ionization of Rydberg helium and lithium atoms in an electric field and define the rhythm attractor to analyze the fractal structures within the framework of the semiclassical closed orbit theory.[8,9] Moreover, we study the influence of the potential energy distribution on the chaotic extent of the ionized electrons and calculate the kinetic energy spectra, which show excellent synchronism to the fractal structures. The symmetrical and iterative properties of the typical closed trajectories are discussed to reveal the dynamic mechanism of fractals within the ionization process of Rydberg atoms.
The paper is organized as follows. In Section
Due to the fact that Rydberg atoms are very sensitive to external fields, we consider helium Rydberg atoms (with only one excited electron) and lithium atoms placed in an electric field directed along the z-axis, respectively. Within the framework of the closed-orbit theory, the outgoing wave packet which propagates away from the atomic core can be described as the evolution of ensemble electron trajectories.[8,9,13] In cylindrical coordinates (ρ,z), the ionization schematic view of the Rydberg system is depicted in Fig.
The Hamiltonian of highly excited electrons in helium atoms with an electric field oriented along the z-axis can be written as

By the scaling law 






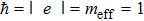
In order to show how the electrons escape in the ionization process, we depict the potential energy distribution of the Rydberg helium and lithium atoms at the same scaled energy 
Three successive magnifications of the escape time plots (icicle map) for the helium atom are shown in Figs. 

In order to identify the rhythm properties in the ionization process, we compute the Hamiltonian motion of the Rydberg helium and lithium atoms based on the canonical equations, which are written as




In Fig. 
We use the escape time curve, which is called the icicle map,[27–29] to provide more detailed insight into the connection between the fractal structure and the escape processes of the ionized electrons. As shown in Figs.
Considering the core scattering effect on the chaotic escape of electrons for the lithium atom, we further study the ionization of the helium Rydberg atom in a pure electric field at the scaled energy ε = −1.3. As shown in Figs. 

We next calculate the kinetic energy spectrum of families of ionizing trajectories. Figures
Moreover, figures
To get a deeper insight into the fractal and the classical trajectories, we calculate the closed trajectories of the ionized electrons of the helium and lithium atoms.
In principle, all the initial outgoing angles should be examined, but we find that the Hamiltonian has a symmetry about z and the ionized electrons escape from the atom in all directions. Therefore, the trajectories can be obtained to research the fractal rhythm in the ionization process. We calculate the fractal dimensions of the escape time plots at different scaled energies for both the helium and the lithium atoms to study the escape behavior of the ionized electrons. For the helium atom, the fractal dimensions of the escape time plots are 


Such rules of closed trajectories and fractal structures occur in many angles, which indicates the scale-free features in the ionization process. The symmetrical shapes of the closed trajectories and the rhythm reflect that the Hamiltonian equations influence the intrinsic dynamics of the ionization systems.
In summary, we have used the semiclassical closed-orbit theory to calculate the ionization fractal rhythm of Rydberg helium and lithium atoms in an electric field. The fractal structures exhibit the nested relationship layer by layer which is defined as the rhythm attractor and present similar rhythm endings in the initial launch angles versus the escape time. Due to the energy distributions of the potentials being distinct, the scattering effects of the helium and lithium atoms show different dynamical impacts on the electrons. In addition, the ionization chaotic regions of the escape time plots tend to broaden as the scaled energy increases for the Rydberg atoms. Oscillations in the kinetic energy spectra of the helium and lithium atoms show excellent correspondence with the fractal structures, which illustrates that the intrinsic dynamic properties of the Hamiltonian equations are closely related to the fractal rhythm. The typical ionizing closed trajectories have been calculated and show iterate properties and perfect symmetry. We believe this work will provide more research methods for revealing new laws in the ionization of Rydberg atoms.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] |









