† Corresponding author. E-mail:
‡ Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant No. 61306113).
It has been reported that the gate leakage currents are described by the Frenkel–Poole emission (FPE) model, at temperatures higher than 250 K. However, the gate leakage currents of our passivated devices do not accord with the FPE model. Therefore, a modified FPE model is developed in which an additional leakage current, besides the gate (III), is added. Based on the samples with different passivations, the III caused by a large number of surface traps is separated from total gate currents, and is found to be linear with respect to (φB−Vg)0.5. Compared with these from the FPE model, the calculated results from the modified model agree well with the Ig–Vg measurements at temperatures ranging from 295 K to 475 K.
AlGaN/GaN high electron mobility transistors (HEMTs) have lots of advantages, such as large critical electrical field, high two-dimensional electron gas (2DEG) density and high saturation velocity. Therefore, AlGaN/GaN HEMTs are suitable for realizing high-power and high-efficiency amplifiers for the next generation wireless communication, satellite communication and radar systems.[1–4] However, excessive gate leakage current in the power AlGaN/GaN HEMT remains a critical challenge. It is commonly believed that the high reverse gate leakage current is tunneling current caused by high-density traps.[5–10] Some of the researchers reported that the reverse gate leakage current is dominated by Frenkel–Poole emission (FPE) under high temperatures (> 250 K) and carrier transport via trapped state near the gate metal/semiconductor interface is a dominant source.[7–9]
In this paper, the gate leakage currents of our passivated devices are found not to accord with those from the FPE model. Thus, a modified model of FPE is developed by implementing an additional leakage current path besides the gate, which is caused by passivation/semiconductor surface traps. In order to separate the additional leakage current from the total current and obtain the modified current expression, two samples of AlGaN/GaN HEMTs are fabricated. One is with ALD-AlN/PECVD-SiNx mixed passivation, and the other is only with PECVD SiNx passivation. It is found that the measured data and the results from the modified model are in excellent agreement with each other at the temperatures ranging from 295 K to 475 K.
The schematic cross-sections of the AlGaN/GaN HEMTs are shown in Fig.
 | Fig. 1. Cross sections of AlGaN/GaN HEMTs: (a) Sample A passivated by PEALD AlN/PECVD SiNx, (b) Sample B passivated by PECVD SiNx. |
The device isolation was formed by Cl2/BCl3 plasma dry etching. Then, the Ti/Al/Ni/Au metal stack deposition was annealed at 850 °C for 30 s in nitrogen atmosphere to realize ohmic contact (0.45 Ω·mm). The source–drain spacing was 8 μm. After that, a 2-μm Schottky gate with Ni/Au (50/200 nm) metal stack was deposited by electron-beam evaporation, located in the middle of the source–drain spacing. Sample A was passivated by 5-nm ALD-AlN and 50-nm PECVD-SiNx at 300 °C, while sample B was passivated only by 50-nm PECVD SiNx at 300 °C.
The temperature-dependent gate current–gate voltage (Ig–Vg) curves of Samples A and B are shown in Fig.
 | Fig. 2. Ig–Vg characteristics of (a) sample A, (b) sample B, and ln(Jg/Er) −
 |
For the high temperatures (> 250 K), the gate leakage current is dominated by the emission of electrons via traps, which is successfully explained by the FPE model. The current density associated with FPE is given by[8]




From Eqs. (
Based on the Poisson equation, the width of the electrons emitting from gate to the surface trap can be expressed as

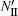
The vertical electric field in region II (as shown in Fig.

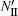



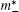
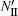



The gate leakage current in region II can be expressed as

Substituting Eqs. (


Based on Eqs. (
In order to obtain the trap states at the gate metal/semiconductor interface by Ct–f characteristics, large area devices are fabricated. The gate areas of sample A′ passivated by AlN/SiNx and sample B′ passivated by SiNx are both 80 μm×100 μm. Figure

Based on Eq. (

The modified model of FPE can be given by


When |Vg| < Vth (|Vg| values for samples A and B are both nearly 3.3 V), the electric field in the semiconductor under the gate metal can be approximately expressed as

Substituting Eqs. (

 | Fig. 6. Comparison of the results from FPE model (red dashed lines), and the modified FPE model (black solid lines) with the measured reverse Ig–Vg data for different temperatures of sample B. |
The modified FPE model is only suitable for the single channel, but unsuitable for the AlGaN/GaN double-channel HEMTs.[14–17] The capacitance in region II (CII) is comprised of CII1 and CII2 (as shown in Fig.
By considering the non-ideal interface states, a modified model of gate leakage current in AlGaN/GaN HEMT is proposed. Comparing with the FPE model, the modified model introduces an additional leakage current path bypassing the gate (III). In order to separate the gate leakage currents, two samples with different passivation are fabricated. III is a linear function of (ϕB − Vg)0.5, which is proved by the plots of temperature-dependent ΔIg−(ϕB − Vg)0.5 of samples A and B. Moreover, the modified gate leakage current model is verified by comparing with the measured temperature-dependent Ig–Vg of sample B, showing excellent agreement. In addition, it should be pointed out that the modified FPE model is only suitable for the single channel, but unsuitable for the AlGaN/GaN double-channel HEMTs.
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 |






