Cite this Article
Wu Ke-Hui†. A review of the growth and structures of silicene on Ag (111). Chinese Physics B, 24(8): 086802  
Permissions
A review of the growth and structures of silicene on Ag (111)
Wu Ke-Hui†a),b)
Beijing National Laboratory for Condensed Matter Physics and Institute of Physics, Chinese Academy of Sciences, Beijing 100190, China
Collaborative Innovation Center of Quantum Matter, Beijing 100871, China

†Corresponding author. E-mail: khwu@aphy.iphy.ac.cn

*Project supported by the National Basic Research Program of China (Grant Nos. 2012CB921703 and 2013CB921702), the National Natural Science Foundation of China (Grant No. 11334011), and the Strategic Priority Research Program of the Chinese Academy of Sciences (Grant No. XDB07020100).

Abstract

Ag (111) is currently the most often used substrate for growing silicene films. Silicene forms a variety of different phases on the Ag (111) substrate. However, the structures of these phases are still not fully understood so far. In this brief review we summarize the growth condition and resulting silicene phases on Ag (111), and discuss the most plausible structural model and electronic property of individual phases. The existing debates on silicene on Ag (111) system are clarified as mush as possible.

PACS: 68.37.Ef; 73.22.–f; 61.48.–c; 71.20.Mq
Keyword: silicene; scanning tunneling microscopy; surface structure; Dirac fermion
1. Introduction

Silicene is a single sheet of silicon atoms arranged in honeycomb lattice similar as graphene. It is a new two-dimensional (2D) silicon allotrope, different from any silicon structure previously found in nature. Silicene has attracted great interest, partially because of its similarity with graphene in both their structure and electronic properties. The study on silicene started with theoretical works. As early as 1994, Takeda and Shiraishi have proposed that silicon can exist in a two-dimensional sheet, [1] and also pointed out the key difference between silicene and graphene: In contrast to graphene where the A and B sublattices are in exactly the same plane, in silicene the two sublattices are relatively shifted in the direction perpendicular to the atomic plane, forming a so-called low buckled structure. However, this work was before the discovery of graphene and not paid too much attention. Following the boom of graphene research, silicene has received renewed interest. Several theoretical papers confirmed the buckled structure of silicene, [2, 3] and the name “ silicene” was also given.[2] Theoretical works also proposed various intriguing properties of silicene, including the existence of Dirac cone, [3, 4] and a larger spin– orbit coupling gap which can result in detectable quantum spin Hall effect (QSHE), [4] and unconventional properties tuned by external electric and magnetic fields[5, 6] as well as by nano-pattering, [7, 8] surface adsorption, [9, 10] and so on.

The breakthrough in experimental research on silicene took place in year 2012, when several groups reported in parallel the successful preparation of a silicene sheet. Among them Takamura group reported the formation of silicene on ZrB2 substrate, [11] whereas other groups, including the Le Lay group, [12] Kawai group, [13] and our group, [14, 15] reported the growth of silicene on Ag (111). It should be noted that before these works, Laimi et al. had claimed the successful growth of silicene on Ag (111) in an earlier work, [16] but their results were not reproduced by other groups. It was also notable that on Ag (111), silicene forms a variety of phases with different superstructures, including the 4× 4, , , and phases.[12– 15] We reported systematically on formation of different phases as a function of the Si coverage and substrate temperature, and also presented the observation of multilayer silicene films.[14] Following the successful preparation of silicene, the study on silicene saw a sudden increase since 2012, and silicene was also reported to be grown on a number of other substrates, such as Ir, [17] MoS2, [18] etc. Moreover, germanene, which is constructed in a similar planar structure by Ge, was also reported to be obtained.[19, 20]

Following the successful preparation of silicene, the focusing issue is then whether silicene indeed exhibits the exotic electronic properties predicted theoretically. To study the electronic structure of silicene, angle resolved photoelectron emission spectroscopy (ARPES) and scanning tunneling microscopy/spectroscopy (STM/STS) were two major experimental techniques. Le Lay et al. reported, together with their silicene structure, the ARPES measurement showing possible existence of the Dirac cone in the 4 × 4 phase of silicene.[12] However, their result was intensively questioned in the following few years.[21– 28] The key issue is that, once a monolayer silicene sheet is placed on a clean Ag (111) substrate, the interaction between the film and the substrate may significantly influence the surface electronic band structure. A number of theoretical papers argued that the Dirac state of silicene no longer exists.[21– 28] Additionally, the experimental work by scanning tunneling spectroscopy (STS) measurements by Lin et al. also found no signature related to a Dirac state.[21] The debates on this issue still continue, although at present most researchers tend to conclude that there is no Dirac state in this system. On the other hand, we mainly focused on the phases for electronic state measurement. We have discovered by STS a series of interesting results, including the quasiparticle interference (QPI) patterns and linear dispersion, [15] suppressed backscattering, [29] low temperature phase transition, [30] and an energy gap which is superconducting-like.[31] These results demonstrated that silicene is a promising playing ground for exotic electronic properties as well as potential applications.

Another most concerned issue of silicene is whether a device based on silicene is possible. However, the study on silicene device meets great challenge, mainly because silicene is not as stable as graphene in air. Once exposed to air, it spontaneously oxidized and no longer exists. Also, currently all the substrates used for silicene are metallic, while for a device a semiconducting or insulating substrate is needed. The attempts to prepare silicene device started from a study on the protection layers, such as Al2O3.[32, 33] A breakthrough occurred recently, where Tao et al. reported an FET device based on silicene films grown on Ag (111), which shows ambipolar transport behavior.[34] This work should inspire more intensive study on silicene devices.

It is notable that, the silicene research is very challenging. The preparation of silicene usually required ultrahigh vacuum (UHV) environment, suitable substrates are difficult to find, and the surface is sensitive to oxidation. Certainly, making silicene devices is far more difficult than the case of graphene. Because of these difficulties, the study on silicene is still in its early stage, and severe debates exist in almost all aspects, including whether alloying occurs during growth, [35– 37] and whether Dirac state exists.[21– 28] These debates, however, should not stop the community from moving forward. Just think about the important fact: The silicon industry has been developed for decades and dominated our life, but a hexagonal silicon sheet, with graphene structure, has just been found in the last few years. One can imagine how strong impact it would have once the intriguing properties of silicene can be introduced to the existing silicon-based devices.

In this brief review, I do not intend to cover all aspects of silicene research. I will focus on a small but important topic, which is the entrance of the silicene world: the growth and atomic structures of silicene on Ag (111). Several years have passed since the silicene growth on Ag (111) was first reported, but there are still many controversies in literature concerning the different structures of silicene on Ag (111). On the other hand, due to the progress in silicene research, some previous unclear issues are now made clear, and so an update of misleading points in literature is necessary. In this mini-review, I will try to give a correct and comprehensive picture on the growth and structures of various silicene structures on Ag (111), covering all debating issues so that the readers would not be confused by conflicting literatures. I will mainly focus on experiment results and analyses. Theoretical calculations will be used mainly to help discussion and understanding.

2. Growth and structure of silicene on Ag (111)

The preparation of silicene film has to be conducted in UHV environment due to the sensitivity of Si upon oxidation. A clean Ag (111) substrate can be achieved by repeated argon ion sputtering and annealing process. Silicon is deposited by thermal evaporation from a pure Si source. The substrate temperature is the key that determines the structure of the resulting silicene film. Depending on the substrate temperature, a variety of reconstructed phases can be observed on Ag (111). When the substrate temperature is low, below about 400 K, silicon atoms deposited on Ag (111) tend to form clusters or disordered structures.[14] When the substrate temperature is above 400 K during deposition, the system experiences five ordered phases: T phase, 4× 4, , , and finally to the phases with increasing substrate temperature. Although these phases appear to be very different in STM images, the key factor is actually not drastic. Mostly they are different due to the rearrangement of the buckling of the surface Si atoms — buckling is the key, intrinsic characteristics of silicene as compared with the planar structure of graphene.

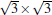
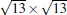
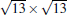
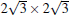
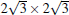
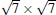
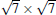
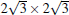
So far, the report of different phases and discussion of their structural models in literature still remain controversy. For examples, the T phase is ascribed to a special phase, [37] the structure of the is still under debated, and the phase is described as “ highly defective and disorder structure” .[38] Apart from these phases, there are occasionally reports of other ordered structures in this system.[16, 39, 40] In this review, we claim that T, 4× 4, , , and phases are the total five ordered Si phases that can be routinely prepared on Ag (111). We will discuss their structure models based on STM observations and first principles calculations. It should be also noted that in literature, the notation of these reconstruction phases is referred to both the pristine silicene-1 × 1 lattice and the Ag (111)-1 × 1 lattice. So that the 4 × 4 phase is also cited as 3 × 3, and the phase as with respective to the Ag (111)-1 × 1. Therefore in the following we will occasionally use Si(3 × 3)/Ag(4 × 4) and Si()/Ag() in order to avoid confusion. The use of silicene 1 × 1 as reference is sometimes useful if the film is not commensurate with the substrate, and it is also convenient to count the number of Si atoms in a theoretical model.

2.1. The T phase

The T phase, reported first by Feng et al., [14] was reproduced in a number of experimental papers, [38, 41] but it has been rarely discussed in literature. In STM images this phase appears as big and round protrusions arranged in a hexagonal closed pack pattern. The distance between neighboring protrusions is about 1.0 nm. Arafune et al. described it as 3.5× 3.5R26° reconstruction, but without detail analysis.[41] Liu et al. suggested that this phase has a periodicity and orientation identical to 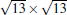phase, so it was ascribed to a special phase.[38]

Fig. 1. The T phase formed at relatively low temperature range. (a) (20 nm× 20 nm) A surface with mostly hexagonal close packed structure of this phase, where small pieces of phase are being nucleated inside the T phase. (b) (50 nm× 50 nm) A surface with better ordered T phase, in some area appearing as long chains.

In our previous paper, [14] we ascribed this T phase as the “ precursor” for the formation of the 4 × 4 phase, the structure of this phase consisting of small pieces of silicene chips instead of a complete honeycomb lattice. Our model of the T phase is based on several experimental facts. Firstly, this phase does not appear in the same temperature regime with other ordered structures. It appears at the lowest temperature regime where ordered Si phases just appear on Ag (111). 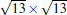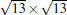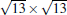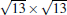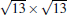Although frequently one can observe coexistence of this phase with 4 × 4 and phases, one can completely kill this phase by annealing the surface at appropriate temperature, leaving only 4 × 4 and phases on the surface. So, the thermal stability of this phase is lower than the 4 × 4 and phases, and thus it should not be included into the phases. Secondly, the periodicity of this phase is different from the other ordered phases. While in literature this phase has been reported as hexagonal close pack of big protrusions, we do often observe other periodic arrangement of the big protrusions, for example as parallel linear chains as shown in Fig. 1(b). We do not consider this parallel chain structure to be a different phase since it has the same formation condition and the same “ basic unit” as the hexagonal one. Thirdly, although normally this phase is imaged as big round protrusions in STM images, in images with atomic resolution one can see significant disorder in this protrusions. They can be recognized as two or three smaller protrusions with different rotations.[14] This further supports our point of view: this phase is likely a partially disordered phase consists of incomplete silicon rings, and it can be regarded as a “ precursor phase” for more ordered phases such as 4 × 4 and . However, the exact atomic structure of this phase is still not clear yet.

2.2. Si(3 × 3)/Ag(4 × 4) phase

The first perfectly ordered phase observed at relatively low temperature is the 3 × 3 phase with respect to silicene 1 × 1, or 4 × 4 phase with respect to the Ag (111)-1 × 1 substrate. The 4 × 4 phase is very easy to recognize in STM images among all different silicene phases on Ag (111), thus it was first reported by several groups in parallel.[12– 14] The STM image of the 4 × 4 phase, as shown in Fig. 2, exhibits triangular half unit cells (HUC), each consisting of three bright spots, which is quite similar to the well-known Si (111)-5 × 5 surface structure. It is notable that between different 4 × 4 domains, one can often observe another phase with a 4 × 4 periodicity, namely the β -4 × 4 phase.[38] It should be noted that β -4 × 4 is not just a domain boundary structure, because the structure can extend to a few unit cell length, indicating a true periodic structure. The reason it appears in the domain boundaries between 4 × 4 phases may be that this phase is less stable than the normal 4 × 4 phase (hereafter noted as α -4 × 4), and that the strain in domain boundary can help to stabilize this phase. The STM images reveal that the two HUCs of the β -4 × 4 phase are different, one with six spots whereas the other has only one spot in the center (see Fig. 2(a)).

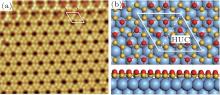Fig. 2. The high resolution STM image and structural model of clean Si(3 × 3)/Ag(4 × 4)-α phase. (a) A typical STM image (14 nm× 11 nm in size). In the upper-right part of the image there is a small area consisting of a metastable-β phase. The white rhombus and the red rhombus mark the α -4 × 4 and β -4 × 4 unit cells, respectively. (b) Structural model of α -4 × 4. Each unit cell consists of 6 upper-buckled Si atoms and the two HUCs are mirror-symmetric (adapted from Ref. [15]).

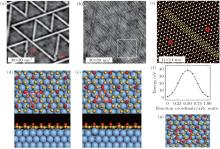
The atomic structure of the 4 × 4-α is relatively easy to be understood.[12] Although at the beginning some different models have been proposed, a general consensus has been reached. It has been known that there is a so-called “ magic mismatch” between the lattice constant of Ag (aAg = 2.88 Å ) and Si (aSi = 3.84 Å ), so that 4 × aAg = 3× aSi within 0.5% of error. Because both the Ag (111) surface and silicene are hexagonal lattices, the simplest model can be constructed by overlapping a low-buckled, free-standing silicene 1 × 1 lattice on top of an Ag (111)-1 × 1 lattice in the same orientation. This naturally results in a commensurate Si(3 × 3)/Ag(4 × 4) superstructure. The commensuration results in minimal interface strain and thus stabilizes the structure.

Overlapping two periodic lattices generally results in “ moiré pattern” , which is commonly observed in graphene on metal surfaces.[42– 45] But in the Si(3 × 3)/Ag(4 × 4) phase, the STM image showing six protrusions in each unit does not correspond to a moiré pattern. They are real Si atoms with higher position. This is due to the rearrangement of buckling configuration of Si atoms. Free-standing silicene-1 × 1 consists of two sub-lattices, A and B, just as the case of graphene. These two sublattices are displaced in opposite direction perpendicular to the film surface. However, once the silicene-1 × 1 sheet is placed on an Ag (111) substrate, the buckling configuration will spontaneously rearrange in order to lower the surface energy. In each Si(3 × 3)/Ag(4 × 4) unit cell there are 18 Si atoms, originally half of them are upper-buckled and half are lower-buckled. But after rearrangement only 6 Si atoms are upper-buckled, and other 12 Si atoms are all lower-buckled, see Fig. 2(b). Moreover, one can see that the 3 upper-buckled Si atoms in one HUC are not in the same sublattice with the 3 upper buckled Si atoms in the other HUC. This is in contrast to the case of free-standing silicene where all upper-buckled Si atoms (or all lower-buckled ones) belong to the same sublattice. Similarly, in the model of silicene β -4 × 4 phase, the registration of the silicene 1 × 1 lattice with the Ag (111) 1 × 1 lattice is identical to the α -4 × 4 phase. The only difference between them is the buckling configuration. In the β phase there are six upper-buckled Si atoms in one HUC, and only one upper-buckled Si atom in the other HUC. Totally there are 7 upper-buckled Si atoms in each UC (see Fig. 4(c)).

Recently, there have been questions on whether the experimentally observed silicene superstructures on Ag (111) is actually Ag– Si alloy phase. Prevot et al. explored in-situ STM measurement during the growth of silicene films, and found that the morphology of the Ag (111) suffers a significant change during growth.[35] They indicated that there is strong Ag mass transport during growth, and thus Ag atoms should be incorporated into the resulting silicene film. However, mass-transport is not a direct proof of the incorporation of Ag in the silicene film. So far, we believe that a pure silicene model without Ag incorporation is still the most plausible model. First, the atomic structure model of the silicene α -4 × 4 is a very natural one. It is energetically stable, and the simulated STM image can perfectly match the experimental observation. In fact, up to now there is still no alloy structure model that can explain the STM images of the 4 × 4 phase. In addition, recently we have conducted a hydrogen adsorption experiment, [46] which further supports the pure silicene structure model, as discussed below.

Hydrogen is the simplest atom. It tends to stick to un-saturated surface atoms with sp3 bonds, such as the Si (111) surface. The Si atoms in silicene have mixed sp2/sp3 hybridization, which weakens their π bond nature, so the Si atoms are partially un-saturated, and they will naturally adsorb one H atom to saturate its dangling bond. For free standing silicene, previous theoretical works proposed that hydrogenation of A and B sublattices from the two opposite sides of the silicene sheet is the most stable.[47– 49] However, on an Ag (111) substrate, only the top side of silicene is accessible to hydrogenation. In such a case the most favorable adsorption site would be the upper-buckled Si atoms. We hydrogenate the silicene α -4 × 4 phase by absorbing atomic hydrogen in UHV. Upon exposing to a saturate hydrogen dose at room temperature, a perfectly ordered structure with the same 4 × 4 periodicity can be observed, as shown in Fig. 3. High resolution image of the hydrogenated structure manifests two inequivalent HUCs, one with six bright spots while the other with only one bright spot in the middle, as shown in Fig. 3(b). The distance between the nearest bright spots is about 3.8 Å , corresponding to the lattice constant of silicene-1 × 1.

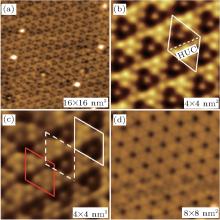Fig. 3. (a) A large area STM image of hydrogenated α -4 × 4 silicene surface showing an ordered 4 × 4 structure. (b) Zoom-in STM image of hydrogenated α -4 × 4 phase. The white rhombus marks an apparent unit cell of the structure. There are six bright protrusions in one HUC and one protrusion in the other HUC. (c) STM image showing the comparison between the position of apparent UCs of clean and hydrogenated α -4 × 4. The red and white rhombus correspond to clean α -4 × 4 UC and the hydrogenated α -4 × 4 UC, respectively. A translation of the white UC (dot line) does not match with the red one. (d) The clean α -4 × 4 surface is fully recovered after annealing the surface at 450 K (adapted from Ref. [46]).

Since the adsorption of H atoms on upper-buckled Si atoms will only increase its degree of buckling, i.e., moves it a little bit upper. The resulting STM image with hydrogenation should be actually not much different from a clean silicene-α -4 × 4 surface. At a first glance this seems to contradict with our observation of significant change of the surface upon hydrogenation — the symmetric 4 × 4 HUCs become asymmetric. But interestingly, the STM image of hydrogenated α -4 × 4 phase looks very similar as the clean β -4 × 4 phase. Indeed, the buckling configuration of silicene changes from α -4 × 4 to β -4 × 4 after adsorbing H atoms. This is fairly easy to understand because in clean surface, the β -4 × 4 phase also prefers to stay in strained area — the domain boundaries between α domains. The adsorption of H atoms will increase the degree of buckling of Si atoms and thus increases the strain, and thus the β phase may become more stable. The perfect agreement of our theoretical model also supports that both the α -4 × 4 and β -4 × 4 are pure silicon structures, see Fig. 4. Indeed, after hydrogenation, one of the HUCs of the 4 × 4 structure becomes a local 1 × 1 structure, corresponding to 1 × 1 arrangements of Si atoms in a honeycomb lattice. There is simply no place to put possible Ag atoms in such a simple 1 × 1 lattice.

Fig. 4. Panels (a) and (b) are the structural model and the simulated STM image of hydrogen-terminated α -4 × 4 and β -4 × 4 models, respectively. Panels (c) and (d) are the structural model and the simulated STM image of hydrogen-terminated α -4 × 4 and β -4 × 4 models, respectively. In panel (c) the white and red rhombuses correspond to the positions of apparent UCs of α -4 × 4 and β -4 × 4 phases, respectively, which are shifted relatively. Note that in panels (a) and (c), the lateral position of Si atoms are fixed unchanged and only the buckling configuration has changed, resulting in the change of the position of apparent UCs (adapted from Ref. [46]).

Another debating issue about the 4 × 4 phase is whether there exists Dirac electron states in the electronic structure. A number of theoretical and experimental evidences show that the Dirac state associated with a free-standing silicene no longer exists in a silicene film on Ag (111).[21– 28] However, interestingly, recently we have directly observed Dirac cones on a surface consisting silicene-4 × 4 on Ag (111) by ARPES.[50] The Dirac cones are present at the edges of the Brillouin zone, and there are twelve Dirac cones. This is in contrast to the theoretical expectation for free-standing silicene that involves six Dirac cones at the K (K′ ) points of the Brillouin zone. The unusual Dirac cone structure is an effect of the silicene– Ag (111) interface, and such interfacial effects may open up new possibilities for investigating quantum phenomena in low dimensional structures.

2.3. The phase

The R13.9° (simplified as ) phase usually co-exist with the 4 × 4 phase.[13, 14, 38] Such a mix-phase film can fully cover the substrate surface with appropriate Si coverage. Depending on the annealing temperature, the area ratio of these two phases can vary notably, but it is usually unlikely to prepare a pure phase surface. This strongly suggests that the 4 × 4 phase and the have very similar thermal stability.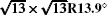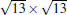

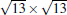
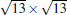
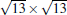
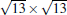
The typical STM images of phase are illustrated in Fig. 5, where one can see the co-existence of the 4 × 4 phase with the phase. When the STM image resolution is not high enough, the two phases will appear very similar, and the phase also has a dark corner hole and triangular unit cells. But the orientation of the phase is rotated by 13.9° with respect to the 4 × 4 phase, as marked in Fig. 5(a). Interestingly, in larger domains of phase, there usually exist long-range periodic patterns, which at a first glance are very similar like moiré patterns. We have observed many different long-range patterns, and figure 5(b) shows several examples.

Fig. 5. (a) Typical STM image of a surface with mix phases of 4 × 4 and . The cross lines indicates the relative rotation of the orientation of the two phases. Panel (b) shows in the same image three domains marked by numbers 1– 3, where different long range, domain boundary patterns can be recognized. The image sizes are (a) 30 nm× 30 nm and (b) 50 nm× 50 nm.

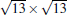
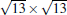
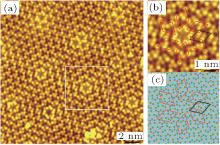High resolution STM images reported by Liu et al. revealed the structure of the phase as well as its “ moiré -like” pattern, as shown in Fig. 6(a).[38] Within a unit cell (marked by the black rhombus), the most prominent feature is a trimer in the center of one half unit cell (HUC), and a protrusion at the corner. The large “ moiré -like pattern” with periodic vortex structure is actually domain wall structure. Each vortex is surrounded by six triangular domains. We can understand the formation mechanism of such domain wall pattern by a symmetry breaking mechanism. Unlike the 4 × 4 phase which can have only one orientation. The R13.9° phase can have two symmetric configurations, depending on the rotation direction — clockwise or anti-clockwise. Under normal preparation condition these two configurations should both present with equal proportion. The system thus chooses a very smart way to satisfy this situation, by spontaneously interlacing the two symmetric domains in a hexagonal pattern.

Fig. 6. (a) High-resolution topography STM image taken on a 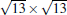domain showing a large hexagonal pattern. U = 3 mV and I = 0.2 nA. (b) Enlarged STM image cut from the square indicated in panel (a). (c) Ball structural model for the vortex pattern shown in panel (b) (adapted from Ref. [38]).

Similar as the 4 × 4 phase, the protrusions that one observed in STM images: the trimer and the spot at the corner, should correspond to rearrangement of the buckling of Si atoms. There have been a number of theoretical models proposed for this phase, [13, 21, 50– 53] as shown in Fig. 7. The simulated STM images were shown in the same figure. One can see that the models (a) and (e) both produce STM images quite similar as the experimental ones, and both of them are possible models. The difference between models (a) and (e) is simply an additional buckled Si atom (red ball). Taking into account the fact that upper-buckled Si atoms and lower-buckled Si atoms should naturally take alternative positions in a silicene lattice, model (a) is more reasonable, while in model (c) all the Si atoms in an HUC are lower-buckled, which should be energetically less favorable.

2.4. The phase

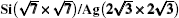
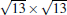
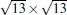
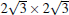
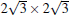
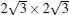
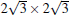
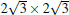
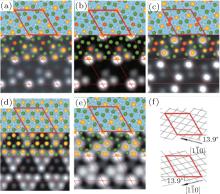The 4 × 4 and phases usually co-exist on the Ag (111) surface and it is almost not possible to obtain a surface with a single phase of either 4 × 4 or . In contrast, the Si()/Ag() phase, reported first by Feng et al., [14] is the only structure that can be prepared with single phase spreading over the entire Ag (111) substrate surface (hereafter we note it as phase). Indeed, by slightly annealing a mix-phase surface containing 4 × 4 and phases, one can obtain a complete phase, and there is no apparent change of the area of the film. This means that the Si density in the 4 × 4, , and phases are almost the same, and that the phase has a higher thermal stability. Therefore this phase is worthy of paying more attention.

Fig. 7. Summary of the atomic structural models proposed previously for the silicene/Ag (111) superstructure. Below each ball model is its corresponding STM simulation result with partial superimposition. Panels (a) and (c) are after Ref. [13], (b) after Ref. [21], (d) after Ref. [51], (e) after Ref. [52]. (h) Schematic illustration showing two sets of 13 × 13 unit cell with rotational angles of ± 13.9° from the direction (adapted from Ref. [38]).

A recent paper by Liu et al. claimed that this phase is too defective to be thermodynamically stable.[39] Here we emphasize that the phase is thermodynamically stable, but it is a challenging issue to understand its atomic structure, especially in the apparently disordered area. Note that recently, Tao et al. reported the FET devices based on monolayer silicene prepared on and then peeled off an Ag (111) substrate.[34] They selected 4 × 4 phase surface and (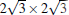)R30° surface as the starting materials. As a result, both devices have basically the same property. It is intriguing because if the 4 × 4 is an ordered phase while ()R30° is severely defective, then their transport behavior such as carrier density and mobility should be very different. In this paper we try to give answers to these issues.

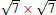
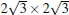
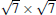
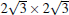
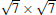
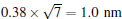
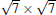
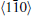
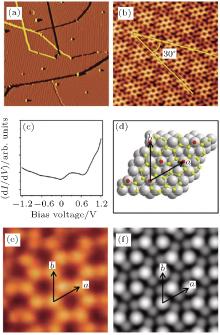Typical large area and zoom-in STM images of the Si()/Ag() phase are shown in Figs. 8(a) and 8(b), respectively. Although the surface is uniform everywhere in a large area, the atomically-resolved structure appears rather defective and disordered. In the large size image one can see periodic pattern of brighter areas. The zoom-in image shows that the brighter region consists of a few hexagonal rings that are perfectly ordered. In contrast, the areas in between the brighter area seem rather disordered. The atomic structure model of the perfect area is relatively easy to understand, as we presented in our early paper with the help of first principles calculations. The model involves a low-buckled silicene lattice on top of the Ag (111)-1 × 1, with the Si- unit cell matching to the Ag- unit cell. Within each Si- unit cell, there is one Si atom which is located exactly on top of an Ag atom, which would appear brighter. This gives a honeycomb lattice with period , in accordance well with our experiment. The angle between the lattice direction of the superstructure and direction of Ag (111) is 30° , which has been confirmed by our experiments.

Fig. 8. (a) A derivative STM image (200 nm× 200 nm, Vtip = 1.43 V) of a surface fully covered by the 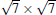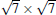phase. (b) High-resolution STM image (15 nm× 15 nm, Vtip = − 1.0 V) showing the atomic structure. The bright areas exhibit complete honeycomb rings with a period of 1.0 nm, while other areas are disordered. (c) dI/dV spectra shows a peak at 0.3 V and a shoulder at 0.9 V are observed. (d) Calculated model of superstructure of silicene. The gray, yellow, and red balls represent the silver, lower silicon, and higher silicon atoms, respectively. (e) and (f) Experimental and simulated STM images (1.0 eV above Fermi energy) showing the similar structure features and unit cell of lattice (adapted from Ref. [14]).

The areas between ordered areas appear disordered and defective. However, carefully inspecting the disordered area, as shown in Fig. 9(a), one can find hidden order everywhere. Around a hole site there are always six spots, not more and not less. Connecting these six spots will result in a hexagon, albeit the hexagon is obvious distorted as compared with the perfect ones in the ordered center. Some of these six spots appear darker, which is the reason why the defective area appears darker than the perfect area. Therefore, although in our early paper we suggested that the large period pattern is due to moiré pattern, it should be more likely to be due to different electronic states in the ordered and disordered areas.

Fig. 9. (a) High resolution STM image of the (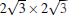)R30° structure with periodic perfect areas surrounded by disordered areas. (b) The structure model proposed by Jamgotchian et al., with a big unit cell (blue diamond) having a superstructure (adapted from Ref. [54]).

We shall emphasize again that the disordered area is not completely disordered. It is most likely that the low-buckled honeycomb structure of silicene is distorted to accommodate the strain, but the basic honeycomb network is still preserved. Recently, Jamgotchian et al. proposed such a kind of structural model, [54] as shown in Fig. 9. Surrounding the perfect area are distorted hexagonal rings that corresponds to disordered area. The real situation should not be exactly same as this model, for example, we observe that the number of hexagonal rings in the perfect area is different from place to place. But the model indeed captures important ingredient of the system. 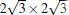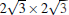In fact, we have recently conducted hydrogen adsorption experiment on the ()R30° surface. Interestingly, after hydrogenation the whole surface can be converted to a complete silicene 1 × 1 structure. This result has two implications. First, the ()R30° surface consists of a complete silicene lattice instead of broken, or fragments of silicene. Secondly, the ()R30° is a pure silicene surface instead of Ag– Si alloy surface, because the resulting silicene 1 × 1 is so simple that one is not able to construct an alloy model with 1 × 1 periodicity. Our results will be published elsewhere.

2.5. phase

As the substrate temperature reaches 500 K, silicene islands with periodicity are observed on the surface. This phase is very interesting due to several experimental facts. Firstly, this phase exhibits a metallic surface state which generates quasi-particle interference (QPI) patterns. It can be probed by STS at low temperature, as shown in Fig. 10. The fitting of the energy– momentum relation of the QPI pattern around a step edge gives linear dispersion which is expected for a Dirac fermion system.[15] Recently we have also measured the decaying behavior of the QPI patterns, and obtained a large decaying factor, which is typical for backscattering suppressed systems like topological insulator or graphene, and different from conventional 2D gas systems.[29] This provides evidences that the phase host Dirac fermions. For comparison, although other monolayer silicene phases are also expected to be metallic, QPI patterns have never been observed on their surfaces. Moreover, a number of intriguing phenomena are also observed in silicene, including the low temperature phase transition, [30] and a superconducting-like gap at zero bias.[31] Finally, we can obtain multilayer silicene film by continue growing Si on the surface, and the surface of the multilayer silicene film exhibits exactly the same structure.[14, 55]

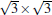
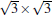
Fig. 10. (a) dI/dV curves taken at 77 K. The position of Dirac point (DP) is labeled. (b) The STM image (40 nm× 40 nm) of 1-ML silicene surface containing an island of the second layer taken at tip bias − 1.0 V. (c), (d), and (e) dI/dV maps of the same area as panel (b) taken at tip bias − 1.0 V, − 0.8 V, and − 0.5 V, respectively. (f) Energy dispersion for silicene determined from wavelength of QPI patterns. The inset shows a schematic drawing of the overall band structure, with the relative location of DP, EF, and our data points (red line) (adapted from Ref. [15]).

The STM image in Fig. 11 shows a silicene island across the step edges of the underlying Ag (111) surface without losing continuity, which is similar to graphene grown on metal surfaces. The high resolution STM image of Fig. 11(b) shows honeycomb structure of silicene terrace. The lattice period of the honeycomb structure is about 0.64 nm, corresponding to a honeycomb superstructure with respect to the 1 × 1 honeycomb lattice.

To account for the atomic structure of the 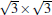phase, it is important to mention the characteristic phase transition at low temperature. When the sample is cooled to liquid helium temperature (5 K), a dramatic structural phase transition occurs, which is characterized by the appearance of atomic chains forming interconnected triangles. A close inspection reveals that these are boundaries separating two symmetric domains, as shown in Fig. 12. At 77 K, the two neighboring protrusions in each honeycomb unit cell are equally bright. While upon the phase transition, one of them becomes much brighter than the other. As there are two possible configurations, the surface is phase-separated into triangular domains with the two symmetric configurations separated by narrow domain boundaries. Temperature-dependent experiments show that the phase transition takes place at about 40 K.

Fig. 11. The STM image of a large area (65 nm× 65 nm) consisting of a sheet of silicene on Ag (111) crossing two substrate steps. (b) The line profile as indicated by the black line in panel (a) shows that the island is of one atom-thick. (c) The high-resolution STM image (10 nm× 10 nm) of the silicene surface taken at tip bias 1.0 V. The honeycomb structure is clearly observed. (d) The line profile as indicated by the black line in panel (c) showing both the lateral and vertical corrugations of the structure observed by STM (adapted from Ref. [15]).

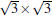
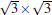
This structure of superstructure can be explained by double symmetric reconstruction structures with dynamic flip– flop motion at high temperature, as shown in Fig. 12(d)– 12(g). These two superstructures have identical geometry if ignoring the substrate, and share the same central substrate atom for each hexagon unit. In each unit cell, only one Si atom is buckled upward, whereas the other five Si atoms have almost the same lower height, resulting in rhombic ()R30° superstructure. The two types of rhombic superstructures accord with the two mirror-symmetric phases observed in low temperature experiments very well. At higher temperature, the flip– flop motion between the two phases results in an averaged, symmetric phase.

So far, there are several debating issues related with the structure. The first one is whether this film is a monolayer silicene or (at least) double layer silicene. In our early paper, we have claimed that this structure exists in both monolayer and multilayer films.[14] In those experiments, we performed growth at relatively high temperature, and only the phase was observed and other phases did not exist. Following our work, several other researchers obtained the same phase by continue growing Si on top of a mix-phase (4 × 4) surface at a relatively low temperature, and islands of surface will form on top of the 4 × 4 film. This makes them conclude that our phase is actually a 2-ML film.[56– 58] In our point of view, these experimental facts indicate that 2-ML and multilayer silicene films all exhibit a structure, and that our previous works were likely performed on 2-ML films. However one still cannot exclude the possibility that monolayer may exist, but rarely observed. The reason is because theoretically the structure is quite stable, and in many other systems such as ZrB2 and Ir (111) substrates, monolayer silicene was indeed observed.[11, 17]

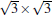
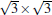
Fig. 12. (a) and (b) The STM images of the same area on 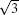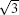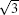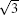R30° silicene taken at tip bias − 2.0 V and 0.1 V, respectively, at 5 K. (c) The filtered high-resolution STM image with high contrast taken at 0.1 V. (d) and (e) Models of two energy-degenerated reconstructed structures of silicene sheet on Ag (111) surface with an orientation angle of θ = 30° , which are obtained from DFT. Color code: Blue, yellow, and red spheres denote Ag atoms, Si atoms in lower layer, and Si atoms in higher layer, respectively. The red triangles denote the units of silicene structures. (f) The interpolated potential energy curve for structural transition between the two the mirror-symmetric geometries on Ag (111). (g) The intermediate structure between the two rhombic structures of silicene shown in panels (d) and (e) (adapted from Ref. [30]).

The second debating issue is whether the structure (on both 2-ML and multilayer silicene film surfaces) is a pure silicone structure, or it is simply the well-known Si (111)-– Ag structure that was conventionally observed in a single crystal Si (111) surface with 1-ML Ag adatoms, as suggested recently by Shirai et al.[59] Indeed, in STM experiments, our phase and the Si (111) -Ag surface appear very similar. Fortunately, recently we can distinctively rule out this possibility by experiments. We first prepared a multilayer silicene film and observed the structure on the surface. And then we used the STM tip to peel off the top layer, exposing the surface of the underneath layer.[60] The high resolution STM image shows the atomic structures of the underneath layer to be , identical to the top layer. As we know, the Si (111) -Ag surface consists of only one layer of Ag atoms on top of pure Si (111) substrate, and it forms at temperature above 700 K. Supposing that our structure comes from Si (111)-– Ag, when we remove the top layer at liquid nitrogen temperature, we should not observe the reconstruction on the underneath layer, which is a pure silicon surface. Therefore, our reconstruction is not the Si (111)-– Ag, but is an intrinsic structure of pure Si. Additionally, there are differences between our and Si (111)-– Ag. For example, although both surfaces exhibit a structural phase transition at low temperature, the transition temperature is drastically different: 30 K-40 K for our phase, and above 150 K for Si (111)-– Ag.

3. Summary

In this brief review we summarized the growth condition and resulting silicene phases on Ag (111), and discussed the most plausible structural model and electronic property of individual phases. The existing debates on silicene on Ag (111) system are clarified as mush as possible. The key issue in the superstructure formation is the rearrangement of buckling which makes silicene potentially more controllable than graphene.

Reference
1 Takeda K and Shiraishi K 1994 Phys. Rev. B 50 14916 [Cited within:1]
2 Guzmań-Verri G G and Lew Yan Voon L C 2007 Phys. Rev. B 76 075131 DOI:10.1103/PhysRevB.76.075131 [Cited within:2]
3 Cahangirov S, Topsakal M, Akturk E, Sahin H and Ciraci S 2009 Phys. Rev. Lett. 102 236804 DOI:10.1103/PhysRevLett.102.236804 [Cited within:2]
4 Liu C C, Feng W and Yao Y 2011 Phys. Rev. Lett. 107 076802 DOI:10.1103/PhysRevLett.107.076802 [Cited within:2]
5 Ezawa M 2012 Phys. Rev. Lett. 109 055502 DOI:10.1103/PhysRevLett.109.055502 [Cited within:1]
6 Ezawa M 2013 Phys. Rev. Lett. 110 026603 DOI:10.1103/PhysRevLett.110.026603 [Cited within:1]
7 Tsai W F, Huang C Y, Chang T R, Lin H, Jeng H T and Bansil A 2013 Nat. Commun. 4 DOI:10.1038/ncomms2525 1500 [Cited within:1]
8 Yamakage A, Ezawa M, Tanaka Y and Nagaosa N 2013 Phys. Rev. B 88 085322 DOI:10.1103/PhysRevB.88.085322 [Cited within:1]
9 Sivek J, Sahin H, Partoens B and Peeters F M 2013 Phys. Rev. B 87 085444 DOI:10.1103/PhysRevB.87.085444 [Cited within:1]
10 Quhe R, Fei R, Liu Q, Zheng J, Li H, Xu C, Ni Z, Wang Y, Yu D, Gao Z and Lu J 2012 Sci. Rep. 2 853 [Cited within:1]
11 Fleurence A, Friedlein R, Ozaki T, Kawai H, Wang Y and Yamada-Takamura Y 2012 Phys. Rev. Lett. 108 245501 DOI:10.1103/PhysRevLett.108.245501 [Cited within:2]
12 Vogt P, Padova P D, Quaresima C, Avila J, Frantzeskakis E, Asensio M C, Resta A, Ealet B and Le Lay G 2012 Phys. Rev. Lett. 108 155501 DOI:10.1103/PhysRevLett.108.155501 [Cited within:5]
13 Lin C L, Arafune R, Kawahara K, Tsukahara N, Minamitani E, Kim Y, Takagi N and Kawai M 2012 Appl. Phys. Express 5 045802 DOI:10.1143/APEX.5.045802 [Cited within:3]
14 Feng B, Ding Z, Meng S, Yao Y, He X, Cheng P, Chen L and Wu K 2012 Nano Lett. 12 DOI:10.1021/nl301047g 3507 [Cited within:11]
15 Chen L, Liu C C, Feng B, He X, Cheng P, Ding Z, Meng S, Yao Y and Wu K 2012 Phys. Rev. Lett. 109 056804 DOI:10.1103/PhysRevLett.109.056804 [Cited within:4]
16 Lalmi B, Oughaddou H, Enriquez H, Kara A, Vizzini S, Ealet B and Aufray B 2012 Appl. Phys. Lett. 97 223109 [Cited within:2]
17 Meng L, Wang Y, Zhang L, Du S, Wu R, Li L, Zhang Y, Li G, Zhou H, Hofer W A and Gao H J 2013 Nano Lett. 13 DOI:10.1021/nl304347w 685 [Cited within:2]
18 Chiappe D, Scalise E, Cinquanta E, Grazianetti C, van den Broek B, Fanciulli M, Houssa M and Molle A 2014 Adv. Mater. 26 DOI:10.1002/adma.201304783 2096 [Cited within:1]
19 Li L, Lu S, Pan J, Qin Z, Wang Y, Wang Y, Cao G, Du S and Gao H J 2014 Adv. Mater. 26 DOI:10.1002/adma.v26.28 4820 [Cited within:1]
20 Dávila M E, Xian L, Cahangirov S, Rubio A and Le Lay G 2014 New J. Phys. 16 095002 DOI:10.1088/1367-2630/16/9/095002 [Cited within:1]
21 Lin C L, Arafune R, Kawahara K, Kanno M, Tsukahara N, Minamitani E, Kim Y, Kawai M and Takagi N 2013 Phys. Rev. Lett. 110 076801 DOI:10.1103/PhysRevLett.110.076801 [Cited within:6]
22 Guo Z X, Furuya S, Iwata J I and Oshiyama A 2013 Phys. Rev. B 87 235435 DOI:10.1103/PhysRevB.87.235435 [Cited within:1]
23 Guo Z X, Furuya S, Iwata J I and Oshiyama A 2013 J. Phys. Soc. Jpn. 82 063714 DOI:10.7566/JPSJ.82.063714 [Cited within:1]
24 Tsoutsou D, Xenogiannopoulou E, Golias E, Tsipas P and Dimoulas A 2013 Appl. Phys. Lett. 103 231604 DOI:10.1063/1.4841335 [Cited within:1]
25 Gori P, Pulci O, Ronci F, Colonna S and Bechstedt F 2013 J. Appl. Phys. 114 113710 DOI:10.1063/1.4821339 [Cited within:1]
26 Cahangirov S, Audiffred M, Tang P, Iacomino A, Duan W, Merino G and Rubio A 2013 Phys. Rev. B 88 035432 DOI:10.1103/PhysRevB.88.035432 [Cited within:1]
27 Yuan Y, Quhe R G, Zheng J, Wang Y, Ni Z, Shi J and Lu J 2014 Physica E 58 DOI:10.1016/j.physe.2013.11.016 38 [Cited within:1]
28 Quhe R G, Yuan Y, Zheng J, Wang Y, Ni Z, Shi J, Yu D, Yang J and Lu J 2014 Sci. Rep. 4 5476 [Cited within:4]
29 Feng B J, Li H, Liu C C, Shao T N, Cheng P, Yao Y G, Meng S, Chen L and Wu K H 2013 ACS Nano 7 DOI:10.1021/nn403661h 9049 [Cited within:2]
30 Chen L, Li H, Feng B, Ding Z, Qiu J, Cheng P, Chen L, Wu K and Meng S 2013 Phys. Rev. Lett. 110 DOI:10.1103/PhysRevLett.110.085504 85504 [Cited within:2]
31 Chen L, Feng B and Wu K 2013 Appl. Phys. Lett. 102 081602 DOI:10.1063/1.4793998 [Cited within:2]
32 Molle A, Grazianetti C, Chiappe D, Cinquanta E, Cianci E, Tallarida G and Fanciulli M 2013 Adv. Funct. Mater. 23 DOI:10.1002/adfm.201300354 4340 [Cited within:1]
33 Friedlein R, Van Bui H, Wiggers F B, Yamada-Takamura Y, Kovalgin A Y and de Jong M P 2014 J. Chem. Phys. 140 204705 DOI:10.1063/1.4878375 [Cited within:1]
34 Tao L, Cinguanta E, Chiappe D, Grazianetti C, Fanciulli M, Dubey M, Molle A and Akinwand e D 2015 Nat. Nanotechnol. 10 DOI:10.1038/nnano.2014.325 227 [Cited within:2]
35 Prévot G, Bernard R, Crugue H and Borensztein Y 2014 Appl. Phys. Lett. 105 213106 DOI:10.1063/1.4902811 [Cited within:2]
36 Rahman M S, Nakagawa T and Mizuno S 2015 Jpn. J. Appl. Phys. 54 015502 DOI:10.7567/JJAP.54.015502 [Cited within:1]
37 Mannix A J, Kiraly B Fisher B L Hersam M C and Guisinger N P 2014 ACS Nano 8 DOI:10.1021/nn503000w 7538 [Cited within:2]
38 Liu Z L, Wang M X, Xu J P, Ge J F, Le Lay G, Vogt P, Qian D, Gao C L, Liu C H and Jia J F 2014 New J. Phys 16 075006 DOI:10.1088/1367-2630/16/7/075006 [Cited within:6]
39 Liu Z L, Wang M X, Liu C, Jia J F, Vogt P, Quaresima C, Ottaviani C, Olivieri B, De Padova P and Le Lay G 2014 APL Mater. 2 092513 DOI:10.1063/1.4894871 [Cited within:2]
40 Kawahara K, Shirasawa T, Arafune R, Lin C L, Takahashi T, Kawai M and Takagi N 2013 Surf. Sci. 623 25 [Cited within:1]
41 Arafune R, Lin C L, Kawahara K, Tsukahara N, Minamitani E, Kim Y, Takagi N and Kawai M 2013 Surf. Sci. 608 DOI:10.1016/j.susc.2012.10.022 297 [Cited within:2]
42 N'Diaye A T, Bleikamp S, Feibelman P J and Michely T 2006 Phys. Rev. Lett. 97 215501 DOI:10.1103/PhysRevLett.97.215501 [Cited within:1]
43 Marchini S, Günther S and Wintterlin J 2007 Phys. Rev. B 76 075429 DOI:10.1103/PhysRevB.76.075429 [Cited within:1]
44 Balog R, Jørgensen B and Nilsson Let al. 2010 Nat. Mater. 9 DOI:10.1038/nmat2710 315 [Cited within:1]
45 Moritz W, Wang B, Bocquet M L, Brugger T, Greber T, Wintterlin J and Günther S 2010 Phys. Rev. Lett. 104 136102 DOI:10.1103/PhysRevLett.104.136102 [Cited within:1]
46 Qiu J, Fu H, Xu Y, Oreshkin A I, Shao T, Li H, Meng S, Chen L and Wu K 2015 Phys. Rev. Lett. 114 126101 DOI:10.1103/PhysRevLett.114.126101 [Cited within:1]
47 Lew Yan Voon L C, Sand berg E, Aga R S and Farajian A A 2010 Appl. Phys. Lett. 97 163114 DOI:10.1063/1.3495786 [Cited within:1]
48 Zheng F B and Zhang C W 2012 Nano. Res. Lett. 7 DOI:10.1186/1556-276X-7-422 422 [Cited within:1]
49 Houssa M, Scalise E, Sankaran K, Pourtois G, Afanas'ev V V and Stesmans A 2011 Appl. Phys. Lett. 98 223107 DOI:10.1063/1.3595682 [Cited within:1]
50 Feng Yet al. arxiv: 1503. 06278 [Cited within:2]
51 Gao J F and Zhao J J 2012 Sci. Rep. 2 861 [Cited within:1]
52 Enriquez H, Vizzini S, Kara A, Lalmi B and Oughaddou H 2012 J. Phys. : Condens. Matter. 24 314211 DOI:10.1088/0953-8984/24/31/314211 [Cited within:1]
53 Jamgotchian H, Colignon Y and Hamzaoui Net al. 2012 J. Phys. : Condens. Matter 24 172001 DOI:10.1088/0953-8984/24/17/172001 [Cited within:1]
54 Jamgotchian H, Ealet B, Colignon Y, Maradj H, Hoarau J Y, Biberian J P and Aufray B arxiv: 1412. 4902. [Cited within:1]
55 Chen J, Li W, Feng B, Cheng P, Qiu J, Chen L and Wu K arxiv: 1405. 7534 [Cited within:1]
56 De Padova P, Avila J, Resta A, Razado-Colambo I, Quaresima C, Ottaviani C, Olivieri B, Bruhn T, Vogt P, Asensio M C and Le Lay G 2013 J. Phys. : Condens. Matter 25 382202 DOI:10.1088/0953-8984/25/38/382202 [Cited within:1]
57 De Padova P, Vogt P and Resta Aet al. 2013 Appl. Phys. Lett. 102 163106 DOI:10.1063/1.4802782 [Cited within:1]
58 Arafune R, Lin C L, Kawahara K, Tsukahara N, Minamitani E, Kim Y, Takagi N and Kawai M 2013 Surf. Sci. 608 DOI:10.1016/j.susc.2012.10.022 297 [Cited within:1]
59 Shirai T, Shiraswaa T, Hirahara T, Fukui N, Takahashi T and Hasegawa S 2014 Phys. Rev. B 89 241403 DOI:10.1103/PhysRevB.89.241403 [Cited within:1]
60 Chen J, Li W, Feng B, Cheng P, Qiu J, Chen L and Wu K unpublished [Cited within:1]