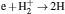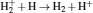†Corresponding author. E-mail: zhaonie@dlut.edu.cn
*Project supported by the National Natural Science Foundation of China (Grant Nos. 11175034, 11205025, 11305023, and 11075029).
A new type of two-dimensional self-consistent fluid model that couples an equivalent circuit module is used to investigate the mode transition characteristics and hysteresis in hydrogen inductively coupled plasmas at different pressures, by varying the series capacitance of the matching box. The variations of the electron density, temperature, and the circuit electrical properties are presented. As cycling the matching capacitance, at high pressure both the discontinuity and hysteresis appear for the plasma parameters and the transferred impedances of both the inductive and capacitive discharge components, while at low pressure only the discontinuity is seen. The simulations predict that the sheath plays a determinative role on the presence of discontinuity and hysteresis at high pressure, by influencing the inductive coupling efficiency of applied power. Moreover, the values of the plasma transferred impedances at different pressures are compared, and the larger plasma inductance at low pressure due to less collision frequency, as analyzed, is the reason why the hysteresis is not seen at low pressure, even with a wider sheath. Besides, the behaviors of the coil voltage and current parameters during the mode transitions are investigated. They both increase (decrease) at the E to H (H to E) mode transition, indicating an improved (worsened) inductive power coupling efficiency.
Inductively coupled plasmas (ICPs) have been extensively used for various semiconductor processes because of their desirable characteristics, such as high plasma density at low pressure, reduced ion damage, and independently controllable ion energy.[1– 4] A main characteristic of these discharges is the existence of two operational modes.[5– 11] One is the E mode, where the radio-frequency (RF) power is capacitively coupled to the discharge and is characterized by a low plasma density and poor luminosity. The other is the H mode where the RF power is inductively coupled to the discharge and is characterized by high electron density and bright light emission. When the input power is increased, the discharge turns from E mode to H mode and the reverse transition happens when decreasing the input power and the transitions between these modes exhibit hysteresis.[12– 14]
At present, there are different arguments about the origin of the hysteresis, i.e., nonlinear behaviors of the plasma and the circuit, impedance matching effect, power loss in the external circuit, etc. El-Fayoumi et al.[15] introduced a capacitive coupling branch onto the discharge circuit and believed that the basic mechanism producing hysteresis is the nonlinearity of the absorbed power due to the sheath width. Lee et al.[16] noticed that the hysteresis was clearly observed only when the pressure was sufficiently high that the multistep ionization is prominent. Thus, they concluded that the multistep ionization was the major factor of the hysteresis. Turner and Lieberman[17] speculated various mechanisms that might cause hysteresis and showed that hysteresis could be qualitatively understood in terms of the power balance, by assuming that either the absorbed power or the dissipated power, or both of them, had nonlinear dependence on the electron density. Daltrini et al.[18] experimentally found that the hysteresis disappeared when the plasma parameters were plotted as the function of real plasma absorbed power. Zhao et al.[19] studied the dynamic characteristics of metastable atoms and their work showed that the presence of metastable atoms had slight effects on the plasma behavior and no evidence of nonlinear mechanisms or hysteresis was observed. Gao et al.[20] found that the matching condition had a significant effect on the hysteresis loop by adjusting the series capacitance of a Γ -type matching network. Experimentally, Lee et al.[21] found that no hysteresis appeared at the auto matching condition, but a significant hysteresis loop at a fixed matching condition at the pressure of 100 mTorr. However, at a higher gas pressure of 350 mTorr, the hysteresis loop was clearly seen at both fixed and auto matching networks.[22]
From the above literature review, we can see that although there is already much theoretical, numerical, and experimental work concerning the origin of the hysteresis, it is still not clear what the predominant mechanism of the hysteresis is. In addition, the matching condition in the circuit is well known to play important roles during the mode transitions and probably is the dominant factor that causes hysteresis. Therefore, detailed studies of the matching effect should be performed. In Ref. [23], the effect of the matching effect on the mode transition behavior in a hydrogen ICP was studied with a new fluid model that is based on our previous mode transition simulation work, [24] but is significantly improved by coupling an equivalent circuit module.[23] In this paper, still using the same model, the effect of the external circuit on the mode transitions and especially the hysteresis, as well as the pressure dependence, is systematically investigated.
This article is organized as follows. In Section 2, the two-dimensional fluid model that consists of the electromagnetic module, fluid module, and equivalent circuit module is described. In Section 3, the simulated mode transition and hysteresis behaviors in the hydrogen ICP at a low pressure of 20 mTorr and a high pressure of 100 mTorr are presented. In particular, the plasma properties themselves and the plasma transferred impedances are investigated. Finally, a conclusion is given in Section 4.
The plasma studied is a planar coil inductively coupled RF plasma source. The discharge reactor is shown in Fig. 1. It has a cylindrical shape with a radius of 12.3 cm and consists of three parts: vacuum vessel, dielectric window, and reaction chamber. The height of the reaction chamber is 12.3 cm. The widths of the dielectric window and the vacuum vessel are 1 cm and 3 cm, respectively. The 13.56-MHz RF power is applied to a four-turn antenna coil through a matching system. The pressure in the reactor is set to be 20 mTorr and 100 mTorr. The reaction chemistry selected is shown in Table 1. The considered species are H+ ions, 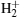

| Table 1. The reactions and rate coefficients for the H2 plasma. |
The model used in this paper consists of three parts, i.e., the electromagnetic module, equivalent circuit module, and fluid module. The model was elaborately described in our previous work[23]. Hence, in the present paper, only a brief introduction is given. Here, note that the plasma properties studied are actually three-dimensional varied in the cylindrical coordinate. However, for the sake of simplification, the planer spiral coils that carry the plasma excitation current are assumed to be sets of concentric rings, and accordingly the variations of plasma parameters and field characteristics in the azimuthal direction are neglected. This is reasonable since in the real plasma sources it is already found that the variations in the azimuthal direction are indeed of minor importance and most of the present modelings in this type of reactor are conducted in radial and axial two-dimensional space. For more details related to this issue, reference [23] can be referred to. (I) The electromagnetic module is used to solve the Maxwell’ s equations within three regions of the reactor, i.e., reaction chamber, dielectric window, and vacuum vessel. Here, the plasma density is assumed to be spatially uniform. With given boundary conditions, one can obtain the analytical expressions of the radio-frequency electromagnetic fields. Details about the derivation of the RF electromagnetic field can be found in Ref. [24]. (II) The equivalent circuit is presented in Fig. 2. It includes RF power source, Γ -type matching box, capacitive, and inductive coupling branches. A 13.56-MHz current source is connected to the matching box. In the matching box, the parallel capacitance C2 is fixed at 1044 pF, and the series capacitance Cs is varied between 100 pF to 120 pF, according to the experiment of our group.[20] The capacitive coupling branch is a series connection of dielectric window capacitance Cq, sheath capacitance, and ohmic heating resistance Rohm of bulk plasma. The inductive branch is a series connection of resistance RH and inductance LH. Here, RH consists of the coil resistance Rcoil and the plasma transferred resistance Rp of the H mode, LH includes the coil inductance Lcoil and the plasma transferred inductance Lp. The coupling scheme of the circuit with the plasma is embodied here through the plasma transferred impedance. More details about the circuit model can be found in Ref. [23]. (III) The fluid module is used to describe the behaviors of all charged and neutral species. The electron dynamics are governed by the equations of continuity, momentum, and energy. Due to their light mass, the inertia term in the electron momentum equation is negligible and thus the drift-diffusion approximation is used. For each ionic species, the equations of continuity and momentum are solved, and for neutral species the continuity equations that consider pure diffusion flux are considered. For both the two species, the temperature is assumed to be in room temperature. Besides, the Poisson equation is solved to obtain the electrostatic field. More details about the fluid equations and their boundary conditions can be found in Ref. [23].
Interactions of the three modules are shown in Fig. 3. The equivalent circuit module calculates electrical properties of the discharge circuit, i.e., voltage drop and flowing current of each electrical element, based on Kichhoff’ s law, and also the plasma transferred impedances that are functions of both plasma parameters and electromagnetic fields through analytic sheath theory and Poynting vector.[23] Among these calculations, the coil current and voltage are selected and inputted into the electromagnetic module to calculate the RF field profiles, by playing the role of specific boundary conditions between the vacuum vessel and the dielectric window. The calculated RF fields are used to calculate deposited power density through the Ohm heating mechanism, and then the power density profile is transported into the energy equation of the fluid module to calculate the electron temperature. The mass, momentum, and energy fluid equations are coupled with each other, and therefore the species densities, momentum, and energy are all calculated at the same time. The calculated electron density and temperature are transported into the electromagnetic module to calculate electron conductivity and plasma current density. This current density is then used in the Maxwell equations to calculate the RF fields. As mentioned before, the plasma transferred impedances are functions of both plasma parameters and RF fields, and so the electron density and temperature from the fluid model, and the RF fields from the electromagnetic module are sent to the equivalent circuit module for calculating the plasma impedances. With the plasma impedances and applied current source, the circuit module starts to calculate the coil electrical properties again. The three modules are iterated with each other until a final steady condition is achieved.
In this section, at a fixed input current (30 A), the mode transition and hysteresis behaviors are investigated by adjusting the series capacitance C1 of the matching box. The dependence of mode transition and hysteresis on the pressure is investigated by setting two pressure values, i.e., 20 mTorr and 100 mTorr. The plasma properties, i.e., electron density and temperature, and the circuit electrical behavior, i.e., inductively transferred plasma impedance, sheath capacitance, etc., are specifically stressed. Moreover, the mechanism that dominates the hysteresis is discussed.
Figure 4 shows the electron density versus the matching capacitance C1 at 20 mTorr and 100 mTorr, respectively. The mode transition and hysteresis behaviors of the discharge are quite different at the two pressures. At low pressure, as C1 increases, the electron density first increases slowly, and the discharge is sustained at E mode with a relative low ne in the order of about 1010 cm− 3. After C1 exceeds 114 pF, ne suddenly increases up to about 1× 1011 cm− 3, which indicates an E to H mode transition. Reversely, when the capacitance is reduced, the electron density first decreases continuously and at certain C1 the abrupt H– E mode transition happens. The value of C1 at which the E to H transition occurs is the same with the reverse H to E transition. Therefore, no hysteresis is observed. At high pressure, however, the E to H transition happens when C1 is 112 pF, while the H to E transition occurs at 108 pF. Thus, a clear normal hysteresis loop is formed. The simulations predict that the hysteresis during the E– H mutual mode transitions occur only when the pressure is sufficiently high, which agrees well with the experiments.[16]
 | Fig. 4. Electron density ne versus the matching capacitance C1 at (a) low pressure of 20 mTorr and (b) high pressure of 100 mTorr. |
Figure 5 presents the electron temperature Te versus the matching capacitance C1 at 20 mTorr and 100 mTorr. At the two pressures, when C1 is low and the discharge is at E mode, the electron temperature is high. Upon increasing the C1, the discharge turns from E mode to H mode, and a sharp drop of Te is observed. Similar to the electron density, the hysteresis is seen at 100 mTorr but not at 20 mTorr.
In Fig. 6, both the transferred resistance and inductance of inductive discharge against the series capacitance at the high pressure 100 mTorr are shown. As seen, the two inductive components evolve with C1 in almost the same ways. They first slowly increase, upon increasing the C1 value up to 111 pF, i.e., from 0.53 Ω to 0.93 Ω for Rp and from 1.48 nH to 2.62 nH for Lp. Then at a certain C1 value of 112 pF, they suddenly jump to very high values that indicates the occurrence of an abrupt E to H mode transition. After the mode transition, these components continually increase but clearly with a higher rate than in the E mode. The increase of the inductive impedances with C1 is logical since the proportion of the inductive discharge is enhanced with the mode transition. Moreover, the increasing rates of the two inductive components while in the E mode are pretty low, as compared with the cases at the mode transition point and in the H mode. This phenomenon, we analyzed, is related to the shield of the wide sheath on the inductive power coupling efficiency at E mode, as revealed by EI-Fayoumi et al. in Ref. [15]. The wide sheath induces a large capacitive impedance that will suppress the inductive power coupling into the plasma (see Fig. 7). The whole system inductance LH, defined as Lc − Lp (see Eq. (9) in Ref. [23]), will decrease with C1, especially when the discharge is at H mode. This is true since the plasma current of the H mode can significantly counteract the coil current itself, as an electrical transformer module revealed.[29] Besides, the maximal reactance induced by the plasma transferred inductance, calculated as ω Lp, is only about 1.5 Ω . This is rather less than the maximum of the resistance Rp, i.e., 8 Ω . Hence at H mode, the transferred impedance is more resistive than inductive, as stated in Ref. [30]. Moreover, we can see that as cycling the C1, both the inductance and the resistance exhibit hysteresis.
 | Fig. 6. Plasma transferred resistance (Rp) (a) and inductance Lp (b) of the inductive discharge component versus the matching capacitance C1 at 100 mTorr. |
 | Fig. 7. Sheath width (a) and transferred capacitance (b) versus the matching capacitance C1 at 100 mTorr. |
In Fig. 7, the sheath width and sheath capacitance versus C1 at 100 mTorr are shown. As seen, when increasing the C1, the sheath width first increases and then decreases in the range of 0.8– 1.0 cm, and the variation is smooth. Nevertheless, at the specific C1 value (112 pF) where the abrupt E to H mode transition happens, it suddenly drops to a very low value, i.e., from about 0.8 cm to 0.4 mm. After the transition, it begins to monotonically decrease at a slow rate. When decreasing C1, the opposite behavior of the sheath width is observed, and again, a hysteresis loop is formed. From Eq. (6), we can see that the sheath capacitance is inversely proportional to the sheath width. Therefore, in Fig. 7(b), the sheath capacitance increases at the E to H mode transition, and deceases at the H to E mode transition. Similarly, the hysteresis loop for the capacitance is seen. Furthermore, in the simulations, the sheath capacitance is found to play determinative roles on the appearance of the hysteresis loop. In particular, the discontinuity and hysteresis both disappear when the sheath capacitance is omitted from the equivalent circuit. Hence, we conclude that the sheath width probably is the determining factor that causes the hysteresis. This conclusion is in accordance with the observation of EI-Fayoumi et al. that the sheath width determined the hysteresis by influencing the inductive coupling efficiency, [15] based on a mixture of electromagnetic theory and circuit analysis (including the sheath capacitance) and by invoking the requirement of absorbed and dissipated power balance.
The coil voltage and coil current versus C1 at 100 mTorr are shown in Fig. 8. As seen, they both increase with C1, and at the E to H mode transition point, they suddenly jump to higher values. As C1 is decreasing, they both decrease, and at the H to E mode transition point, they suddenly drop to low values. Interestingly, they both exhibit hysteresis. The behaviors of the coil voltage and current with C1 indicate that the inductive coupling efficiency is indeed varied along with the mode transitions, and more importantly, the efficiency is greatly improved at the E to H mode transition point, as expected by much published work.[5, 14]
The plasma transferred resistance and inductance of inductive discharge component against C1 at 20 mTorr are shown in Fig. 9. The behaviors of the inductive impedance components with C1 at the low pressure are the same as the plasma parameters that are shown in Figs. 4(a) and 5(a). They only exhibit discontinuities at the mode transition points, but no hysteresis appears as cycling C1. Moreover, due to the low electron collision frequency at low pressure, the transferred resistance value, with its maximum of 4 Ω , is lower than the magnitude at high pressure with its maximum 8 Ω , as shown in Fig. 6(a). Nevertheless, in Fig. 9(b), this lower collision frequency reversely leads to higher plasma inductance, characterized with its maximum of 0.06 μ H that is three times of the value of high pressure, 0.02 μ H, in Fig. 6(b). As analyzed before, a higher plasma inductance can significantly counteract the coil inductance, thus reducing the whole system inductance. Consequently, the shielding role of the wide sheath in the ICP discharge with low system inductance will be severely abated. This mechanism we proposed is probably the reason why the hysteresis is not formed at low pressure even with a wider sheath (see Fig. 10) as compared with high pressure. In Fig. 10, the sheath width and the transferred capacitance versus C1 at 20 mTorr are shown. The sheath width decreases and the sheath capacitance increases both monotonically with the C1. As compared with the case of high pressure in Fig. 7(a), we can see that the sheath width at low pressure is larger than the case of high pressure, e.g., 1.7 cm at 20 mTorr versus 0.9 cm at 100 mTorr when C1 is 105 pF. This is because the ne of 20 mTorr at 105 pF, i.e., 6× 109 cm− 3, is rather lower than the high pressure, i.e., 1.8× 1010 cm− 3. The lower density at low pressure is due to the low neutral density and thus the low ionization rate.
 | Fig. 9. Plasma transferred resistance (a) and inductance (b) of inductive discharge component versus the matching capacitance C1 at 20 mTorr. |
 | Fig. 10. Sheath width (a) and transferred capacitance (b) versus the matching capacitance C1 at 20 mTorr. |
In this paper, an improved fluid model based on our previous work and that couples the equivalent circuit module, is used to investigate the discontinuous mode transition and hysteresis in a hydrogen inductively coupled plasma. Particularly, the electron density and temperature, and the plasma transferred circuit impedances are investigated by adjusting the series capacitance of the matching box at different pressures. The results show that at low pressure, as the matching capacitance increases, the discontinuities of both the electron density and temperature with the capacitance are observed during the mode transition. However, no hysteresis appears as cycling the capacitance. At high pressure, both the discontinuity and hysteresis of the electron parameters are observed. The inductive plasma transferred impedance studied here includes the inductance and resistance, and the capacitive impedance considered is the sheath capacitance. As for the plasma itself, these impedances, together with the sheath width, all exhibit hysteresis at high pressure, but only discontinuity at low pressure. Our simulations predict that the sheath capacitance plays a determinative role on the appearance of both discontinuity and hysteresis, by influencing the inductive coupling efficiency of applied power. Moreover, the failure of hysteresis appearance at low pressure, even with a wider sheath, is probably due to a low system inductance caused by a large plasma transferred inductance of low pressure. Besides, the evolutions of the coil voltage and current are investigated. The coil electric parameters also show discontinuity and hysteresis at high pressure. More importantly, they both abruptly increase at the E to H mode transition point, and decrease at the reverse case, implying a better (worse) inductive power coupling efficiency at E to H (H to E) mode transition. In future work, the electron Monte Carlo part will be included into this model to examine the evolution of the electron energy distribution function (EEDF), for better understanding the mechanism of hysteresis.
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|
| 17 |
|
| 18 |
|
| 19 |
|
| 20 |
|
| 21 |
|
| 22 |
|
| 23 |
|
| 24 |
|
| 25 |
|
| 26 |
|
| 27 |
|
| 28 |
|
| 29 |
|
| 30 |
|