† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant No. 21875024).
A sequential of concepts developed in the last decade has enabled a resolution to multiple anomalies of water ice and its low-dimensionality, particularly. Developed concepts include the coupled hydrogen bond (O:H–O) oscillator pair, segmental specific heat, three-body coupling potentials, quasisolidity, and supersolidity. Resolved anomalies include ice buoyancy, ice slipperiness, water skin toughness, supercooling and superheating at the nanoscale, etc. Evidence shows consistently that molecular undercoordination shortens the H–O bond and stiffens its phonon while undercoordination does the O:H nonbond contrastingly associated with strong lone pair “:” polarization, which endows the low-dimensional water ice with supersolidity. The supersolid phase is hydrophobic, less dense, viscoelastic, thermally more diffusive, and stable, having longer electron and phonon lifetime. The equal number of lone pairs and protons reserves the configuration and orientation of the coupled O:H–O bonds and restricts molecular rotation and proton hopping, which entitles water the simplest, ordered, tetrahedrally-coordinated, fluctuating molecular crystal covered with a supersolid skin. The O:H–O segmental cooperativity and specific-heat disparity form the soul dictate the extraordinary adaptivity, reactivity, recoverability, and sensitivity of water ice when subjecting to physical perturbation. It is recommended that the premise of “hydrogen bonding and electronic dynamics” would deepen the insight into the core physics and chemistry of water ice.
—Coordination bonding and electronic dynamics govern the performance of substance[1]
Laid the platform for defect physics, surface chemistry, nanoscience, and nanotechnology, atomic or molecular undercoordination amazed the mysterious water ice even further.[2–4] For instances, the skin of water is toughest, and ice is naturally most slippery of ever known.[5–9] The extent of slipperiness and toughness increases with the curvature of the surface, making a nanodroplet and a nanobubble more chemically reactive but mechanically and thermally endurable.[10–13] A water droplet bounces rounds before it disappears when falls on water, showing both skins elastic and hydrophobic. Water droplets encapsulated in the hydrophobic pores and ultrathin water films deposited on the hydrophobic surfaces of graphite, silica, protein, and selected metals behave like ice at the ambient temperature.[14–18] Kept a 0.6 nm thick air-gap between its skin and the wall, water droplet travels through a microchannel at a speed much faster than what the classical fluid theory could expect.[19] The nanometer-sized droplet melts at a temperature of some 50 K higher than the bulk melting point, Tm = 273 K;[20] contrastingly, a droplet of 1.4 nm across freezes at 205 K,[21] compared to the bulk freezing point, TN = 258 K.[22] Table
The low-dimensional water ice is ubiquitously important to the quality and sustainability of human life.[8] Considerable effort has been made to the understanding of anomalies of water and ice, at the molecular and nanoscale level, particularly, since 1859 when Faraday and Thomson[23,24] firstly noted that a liquid-like layer not only makes ice slippery but also welds two blocks of ice – known as ice regelation.[25,26] A verity of experimental techniques have been used to explore the performance of molecules, protons, and electrons in the spatial-temporal-energetic domains, such as low-energy electron diffraction (LEED),[27] neutron[21] and proton[28] diffractions, atomic force microscopy (AFM),[20] and scanning tunneling microscopy/spectroscopy (STM/S).[29] Photoelectron spectroscopy of x-ray (XPS)[30,31] and ultra-violet (UPS)[32] excitation and phonon spectroscopy of Raman scattering,[22] infrared transmission,[33] nuclear magnetic resonance (NMR),[34] and sum frequency generation (SFG)[35,36] have contributed immensely to the advancement of this field.
Theoretically, the classical continuum thermodynamics deals with water and ice as a collection of gaseous-like neutral particles to examine the response of the entire body to stimuli, which succeeds in formulating the liquid–vapor phase transition in terms of enthalpy, entropy, and Gibbs free energy.[37,38] Molecular dynamics (MD)[39–43] treats the flexible or rigid, polarizable or non-polarizable, individual molecular dipole as the primary unit of structure. Combining MD computations and ultrafast phonon spectroscopy reveals spatial–temporal performance of molecules with derived information of phonon relaxation or the molecular residing time in a specific coordination site, and the manner and mobility of mass transport. An interlay of STM/S and MD simulations of the proton quantum effect has enabled visualization of the two-dimensional ice formation[44] and the concerted tunneling of protons within a water cluster with quantification of the impact of zero-point motion on the strength of single hydrogen bond at a water/solid interface.[29] Density functional theory (DFT) calculations resolve the perturbation derived relaxation of the O:H–O segmental length and vibrational frequencies.[22,45] The perturbation refers to electrostatic polarization, mechanical compression, molecular undercoordination, thermal excitation, charge injection by aqueous solvation, etc.
| Table 1. Typical examples for the molecular undercoordination resolved anomalies of low-dimensional water ice. . |
This presentation shows the essentiality of the sequential rules and concepts developed in the last decade to resolve anomalies of water ice and its low-dimensionality. Focus is on the “local bonding and electronic dynamics” towards deeper understanding of the core physics and chemistry of water ice. Evidence shows consistently that molecular undercoordination driven O:H–O cooperative relaxation, nonbonding electron polarization, and specific-heat dispersion resolve a common supersolid skin that is hydrophobic, less dense, reactive, viscoelastic, and thermally more stable. It is also uncovered that the supersolid skin is thermally more diffusive with a lower specific heat. The supersolidity reconciles the anomalies such as ice floating, ice slipperiness, superfluidity, and hydrophobicity of low-dimensional water and ice.
—Interionic repulsion entitles O:H–O a coupled oscillator pair and water the simplest molecular crystal[4]
As the basic functional and interaction elements of molecular crystals, the equally numbered electron lone pairs “:” and dangling protons (H+ simplified as H) entitle water the simplest, ordered, tetrahedrally-coordinated, uniform yet fluctuating structure among known molecular crystals. Represented using a H2O:4H2O tetrahedral motif with one H2O molecular in the center and four on the apical sites, water reserves its O:H–O configuration and orientation over broad pressure and temperature ranges, from 5 K to 2000 K and from 10−11 Pa to 1012 Pa.[71,72] H2O molecular rotation is subject to restriction. Rotating a H2O molecule around its C3v-axis by 120° causes long-range disorder of its two-dimensional hexagonal latticed ice[73] because of the presence of repulsive H↔H and O:⇔:O interactions.[74] H+ transitional tunneling or hopping is also restricted from one asymmetrical site to the other between adjacent oxygen atoms because dissociating a H–O bond of 5.1 eV energy in the vapor phase requires a 121.6 nm laser radiation.[70]
In placing the molecular wise, the O:H–O bond, as the basic functional and structural unit, features the performance of electrons, bonding, and molecules in the energetic-spatial-temporal domains. The strong repulsion between lone pairs of adjacent oxygen anions endows the O:H–O an asymmetrical, short-range, and coupled oscillator pair that integrates the intermolecular O:H nonbond and the intramolecular H–O polar-covalent bond interactions. The O:H–O bond responds to a physical perturbation cooperatively in relaxing its segmental length and energy and electronic dynamics.[75]
Figure
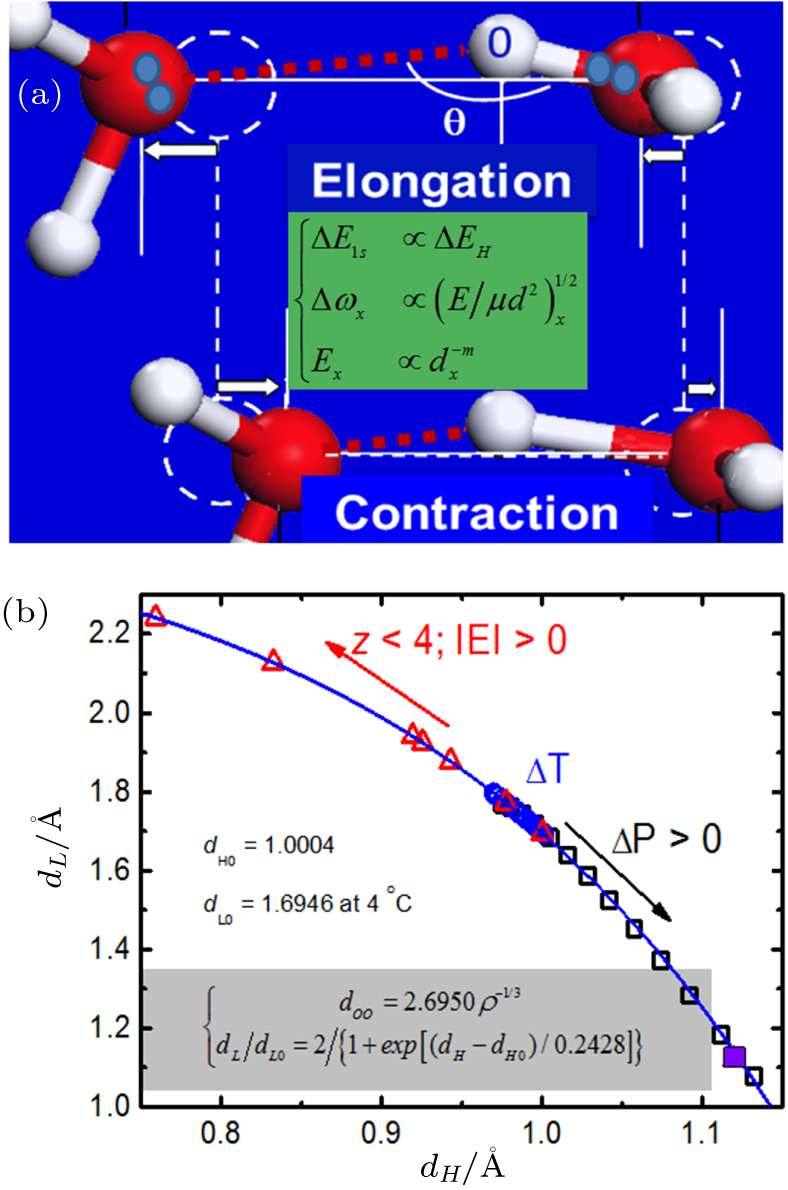 | Fig. 1. O:H–O segmental length cooperative relaxation.[63,78] (a) O—O distance changes by shortening one segment and lengthening the other because of coupling interaction. The O:H always relaxes more than the H–O does because of the O:H–O segmental disparity. The primary rule for (b) O:H–O length cooperativity by compression (p), thermal excitation (t), molecular undercoordination (z), and electrostatic polarization (e). |
Water absorbs energy through H–O bond contraction and emits energy at its length inversion. The O:H relaxation dissipates energy caped at ∼ 0.2 eV through molecular thermal vibration or even evaporation. The length, energy, and the stretching vibration frequency (dx, Ex, ωx) of the H–O are about (1.0 Å, 4.0 eV, 3200 cm−1) and those of the O:H are about (1.7 Å, 0.2 eV, 200 cm−1) at 277 K of maximal mass density, ρM = 1.0 g/cm−3.[51] The bond angle, segmental length, and the O—O repulsion undergo fluctuation.
Figure The O 1s binding-energy shifts proportionally to the H–O bond energy, ΔE1s ∝ ΔEH, while ΔEL is too small to make significant contribution. The segmental stretching vibration frequency ωx depends functionally on the segmental length dx, energy Ex, and its reduced mass μx of the oscillator. The segmental cohesive energy Ex is inversely proportional to its length dx with m > 0 being the bond nature index.
Figure
—O:H–O segmental stiffness and energy define its specific heat and multiphase density oscillation[79]
Because of the segmental disparity in stiffness, introducing the specific-heat of Debye approximation, ηx(T/ΘDx), is necessary for each segmental to describe the response of the O:H–O bonds to thermal excitation.[79] The specific-heat is the energy required to raise the segment temperature by 1 K. The thermal integration of ηx(T/ΘDx) from 0 K to the evaporation temperature, TVx, at which segment thermal rupture occurs, equals the segmental cohesive energy Ex. The phonon frequency ωx determines the Debye temperature ΘDx through Einstein’s relation ΔΘDx ∝ Δωx. Therefore, an external perturbation mediates the ηx(T/ΘDx) curves through ωx and Ex relaxation. The ηx(T/ΘDx) of lower ΘDx approaches to its saturation more quickly. The known (ωx, Ex, ΘDx) = ∼ (200 cm−1, 0.2 eV, 192 K) for the O:H and ∼ (3200 cm−1, 4.0 eV, 3200 K) for the H–O bond in the bulk water derived the ΘDH/ΘDL = 3200/192, which yields the respective ηx(T/ΘDx) curves, as shown in Fig.
 | Fig. 2. Specific-heat disparity and multiphase thermal mass density oscillation.[79] (a) Intersection points define the quasisolid phase (QS) whose boundaries close to temperatures for homogeneous ice nucleation (TN) and melting (Tm). Molecular undercoordination disperses the QS boundary outwardly by H–O contraction and O:H elongation through Einstein’s relation. (b) Segmental specific-heat ratio defines the thermal slope of density over all phases for water ice and the critical temperatures vary with volume size at the nanometer scale (T ≥ 273 K bulk water; T ≤ 273 K 1.4 nm sized droplet).[21] |
The interplay of the segmental ηx(T/ΘDx) determines the thermodynamics of water ice. The superposition results in two intersecting points and reproduces the critical temperatures for boundaries of the known phases displayed under atmospheric pressure,[22] see Fig.
Most strikingly, the superposition of the ηx(T/ΘDx) creates the ever unaware quasisolid phase (QS) whose boundaries (ηL/ηH ≡ 1) correspond to extreme densities and close to temperatures for melting Tm (277 K, 1.0 g/cm3) and freezing TN (258 K; 0.92 g/cm3). The TN shifts from 258 K to 205 K when turning the bulk water into 1.4 nm sized droplet.[79] The ΔTN ∝ ΔTV ∝ ΔEL and ΔTm ∝ ΔEH relations hold roughly though dispersion of the specific heat curves. In the QS phase (ηL/ηH > 1), cooling shortens the dH less than the dL elongates and the volume expands gradually to a maximum at the TN, which clarifies why ice floats. It would be proper to define 277 K as the Tm because the density profile shows no transition at Tm = 273 K.
In the vapor phase (ηL ≅ 0), the O:H interaction is negligible, and the gaseous molecule can be taken as an isolated structure unit that has the shortest H–O bond. In the liquid and Ic + h phases (ηL/ηH < 1), dL cooling contracts more than dH elongates, so density increases at different rates. Liquid water and Ic + h ice follow the regular rule of thermal expansion, but it is in a completely different mechanism. The energy storage by the dH thermal contraction is prerequisite to the Mpemba effect for energy emission at cooling.[55] In the XI phase, the ηx(T/ΘDx) approaches zero, ηL ≅ ηH ≅ 0, O:H–O segmental length and energy are insensitive to thermal excitation, Δωx ≅ 0.[80,81] The cooling ∠O:H–O angle expansion from 165° to 175° lowers slightly the mass density.[21]
—Undercoordination shortens and stiffens the H–O bond and polarizes lone pairs[22]
Figure
 | Fig. 3. Undercoordination resolved bond relaxation and O:H–O potentials.[1,82,85] (a) BOLS formulation of atomic undercoordination-resolved bond contraction (z < 12), with m > 0 being the bond nature index. (b) O:H–O potential paths for the sized (H2O)N = 2 – 6 clusters (ΔdH < 0, ΔEH > 0; ΔdL > 0, ΔEL > 0). The blue dots in (b) are the initial equilibrium for N = 6. |
Likewise, water molecular undercoordination shortens and strengthens the H–O bond but lengthens and softens the O:H nonbond contrastingly and cooperatively of the coupled O:H–O bond associated with strong polarization.[84,4] H–O bond contraction my not follow exactly the primary BOLS law quantitatively because the O—O coupling interaction. Figure
 | Fig. 4. O:H–O bond segmental length cooperative relaxation. O—O repulsion dislocates O ions in the same direction by different amounts (insets) under (a) mechanical compression, cooling of (b) liquid and (c) quasisolid (QS) phase (in units of °C), and (d) undercoordination by reducing the (H2O)N size from N = 6 to 2. Arrows denote the master pieces and their relaxation directions. The H–O bond always relaxes less than the O:H and both of them relax contrastingly in their curvatures and slopes, irrespective of the applied stimulus or the structural order because of the O–O Coulomb repulsive coupling (reprinted with permission from Ref. [63]). |
Molecular undercoordination not only disperses the QS boundary outwardly by ωx relaxation but also strongly polarizes the QS phase, leading to the skin supersolidity that is hydrophobic, less dense, lubricate, mechanically and thermally more stable, diffusive, and viscoelastic. The supersolidity is extended from the elastic and repulsive contacting interface between Helium fragments that undergo frictionless motion at mK temperatures.[86] Existing throughout the volume, the QS arises from specific-heat disparity but the supersolidity results from polarization by molecular undercoordination. The supersolidity enhances the QS phase at bonding network ends such as defects, skins, droplets, hollow bubbles and skins of bulk species, regardless of the structure phase and it is thermally insensitive. Quasisolid undergoes cooling volume contraction and the supersolidity is subject to undercoordination expansion. Droplet size reduction increases the fraction of undercoordinated molecules and reduces the effective molecular coordination number (CN) of the skin. The droplet-size-induced ΘD x(ωx) relaxation mediates the specific-heat and hence disperses the extreme-density temperatures or boundaries of the QS. The QS dispersion by undercoordination lowers the TN and TV and raises the Tm, leading to the superheating and supercooling phenomena observed from bubbles and droplets.
—Perturbation relaxes the O:H–O segmental length cooperatively in a ‘master–slave’ manner[63]
The O:H–O cooperative relaxability is proven universally true. Figure
Figure
Results confirmed that (a) mechanical compression and (d) molecular undercoordination effect oppositely on the O:H–O relaxation and that the O:H–O responds to cooling contrastingly in (b) the liquid and (c) the QS phase, confirming the O:H–O cooperativity theoretical predictions. Raman spectroscopy investigations[22,75,79] confirmed the corresponding O:H–O bond stiffness relaxation. Preliminary results showed the efficiency and essentiality of the BOLS-NEP and coupled O:H–O bond theories in dealing with water ice, which opened the entrance and paved the path directing to the core physics and chemistry of water and ice.
—O:H–O segmental length and stiffness are rather sensitive to the coordination environment[53]
Figure
 | Fig. 5. Skin O:H–O segmental length and stiffness cooperative relaxation.[53] Length and stiffness (inset) transition for the (a) H–O bond and (b) O:H nonbond from the bulk value (b) to the skin (s) and to the H–O free radicals (r). Inset (a) shows the complex unit cell denoted with bulk, skin, and a vacuum slab. The P components arise from the screening and splitting of the crystal potentials by polarization. |
Wang and co-workers[45,88] examined using DFT calculations the site and orientation resolved electronic binding energy and H–O stretching vibration for the sized (H2O)n clusters (n = 17, 19, 20, 21, 23, and 25). The H–O bonds are classified into five groups according to their coordination environments: the dangling H–O bonds (D), the H–O of the O:H–O formed between the dangling H2O molecules (C), those of the O:H–O formed between the H2O molecules without dangling H–O bonds, and those of the O:H–O bond between the tetrahedral-coordinated H2O and its neighboring molecules. The calculated spectra in Fig.
 | Fig. 6. Computational H–O stretching vibration modes in the (H2O)n clusters.[88] The black dashed lines convolute the H–O vibration modes of the entire clusters. The sharp feature D corresponds to the H–O dangling bonds, C to the H–O of the O:H–O bonds between molecules at rims, features A and B to the H–O bonds inside the clusters. Reprinted with copyright permission from Ref. [88]. |
—DPS resolves O:H–O phonon transition from the modes of ordinary water ice to its supersolid[74]
Figure
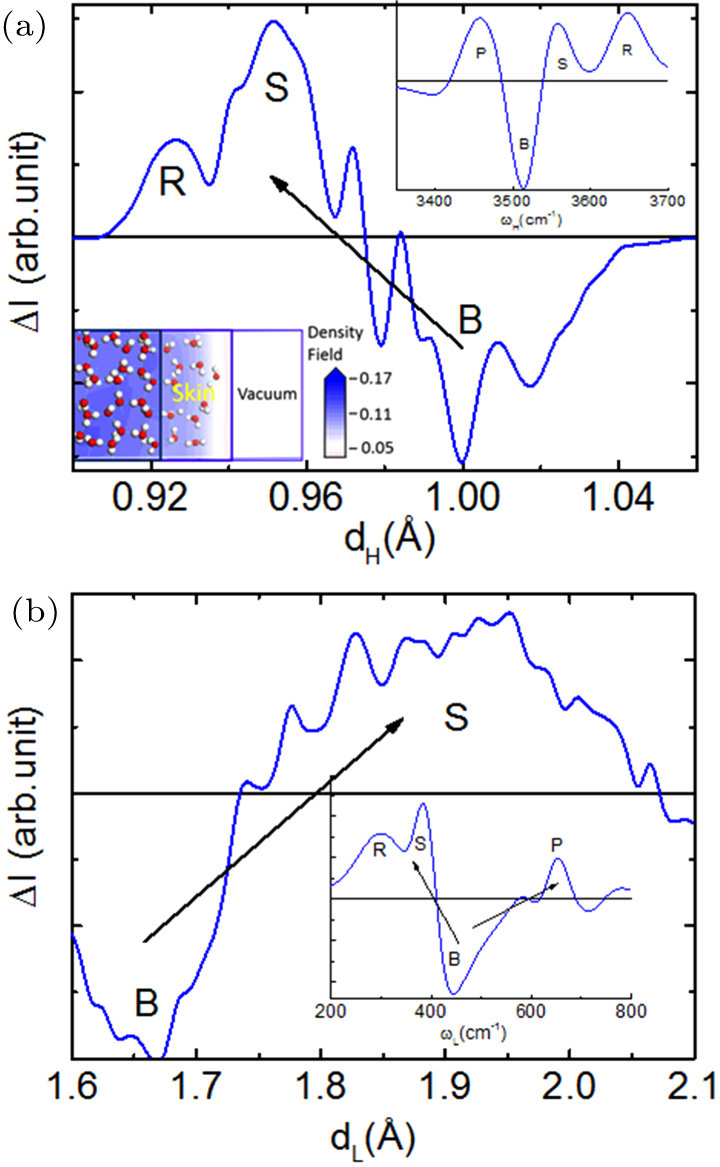
 | Fig. 7. H–O stiffness transition from the bulk to the skins of large volumes and nanodroplets.[53,74] (a) Skins of 298 K water and (253–258) K ice[65] share an identical ωH of 3450 cm−1 and the (b) D–O phonon[33] transits from below 2550 to its above for the skin of droplet. Insets show ice slipperiness, water skin toughness, and the elasticity and hydrophobicity of skins of droplet and water. |
Results confirmed again that molecular undercoordination does shorten the H–O and the D–O bond and stiffen their phonons. Strikingly, skins of water and ice share an identical ωH of 3450 cm−1. The DPS peak integrals suggest that the skin of ice is 9/4 times thick of the liquid, because of thermal fluctuation. The identical ωH says that neither a layer of ice (3150 cm−1) covers the liquid nor a liquid overlayer (3200 cm−1) stays on ice, instead, skins of both liquid and ice share the same supersolidity of identical H–O bond of 3450 cm−1 vibrating frequency.
One can estimate the skin shell thickness of the core-shell structured droplet. Integrating the DPS peaks in Fig.
SFG measurements[35] uncovered the site and orientation resolved H–O bond vibrating frequencies on the outmost two molecular layers of ice Ih (0001) surface. The frequency of the H–O bond (H–OB1) pointing from the first to the second sublayer is above 3270 cm−1 and the H–OB2 from the second to the first layer is below 3270 cm−1 because of the coordination environment. This discovery is consistent with the DFT derivatives[90] and the present BOLS expectation.[85,91] The less coordinated H–OB1 is shorter and stiffener than the H–OB2. The frequency of the dangling H–O bond is 3700 cm−1 measured by SFG and 3610 cm−1 by Raman reflection under the ambient temperature.
The skin supersolidity is responsible, as Fig.
—Skin H–O contraction entraps the core and bonding electrons and polarizes lone pairs[76]
The energy level of an isolated atom shifts deeper when a large volume is formed as the interatomic interaction comes into play. The energy shift is proportional to the single bond energy, according to tight-binding approximation with omitting the tiny overlapping integral between the same core orbits of adjacent atoms.[92] Atomic undercoordnation shifts further the core level because of the spontaneous bond contraction. XPS and UPS data in Fig. 
 | Fig. 8. Site and orientation resolved SFG H–O vibration frequency. Undercoordination resolves the frequencies of the OB1:H–OB2 and the OB1 – H:OB2 bonds (inset) between outermost two sublayers of the ice Ih(0001) skin.[35] Insets illustrate segmental bond lengths, orientations, and frequencies of the H–O stretching vibrations. The positive peak (< 3270 cm−1) corresponds to the H–OB2 vibration (shaded in green) and the valley (> 3270 cm−1) to the OB1-H (shaded in blue). The less coordinated OB1-H is shorter and stiffer and its H:OB2 is longer and softer than the OB1:H–OB2. |
 | Fig. 9. Undercoordination induced quantum entrapment and polarization.[31,63,64,67,68] (a) The O 1s energy shifts from the bulk value of 536.6 eV to 538.1 eV for the skin and to 549.7 eV for gaseous state. (b) The hydrated nonbonding electron shifts its energy from the core value of 2.4 eV and the skin of 1.2 eV to the limit of 0.4 eV for N = 5 cluster. Inset (b) shows the cluster size dependent ωH blueshift.[4] |
Near edge x-ray absorption fine structure (NEXAFS) reveled the 535 eV predge and a 531 eV gaseous O2 peak for high-density oxygen infilled nanobubbles.[93] The peaks result from the energy difference between the inner O 1s level and the uppermost level,[89] ΔEXAS = EV – E1s = 531 eV and 535 eV for O2 gas within the bubble and the liquid H2O, respectively. The ΔEO2 – ΔEH2O = – 4 eV indicates that the uppermost EV level and the E1s for O2 gas are deeper than corresponding ones of liquid H2O.
Due to the local polarization, an oxygen atom gains net charge from –0.616e to –0.652e when moves from the bulk to the skin.[53] This charge gain enhances further the O—O repulsion at the surface. A free electron injected into water serves as a probe to the local environment without changing the solvent geometry. The hydrated electron will be trapped by the locally oriented H2O molecules, forming a (–)⋅ 4 H2O motif in contrasting to the polarity of the Na+⋅ 4 H2O.[94] The ultrafast pump–probe liquid-jet UPS[32,64,67,68] probed, see Fig.
—Viscoelasticity and dipolar repulsivity retard carrier dynamics mainly by reflection[89]
Electron or phonon lifetime τ probed using ultrafast spectroscopy fingerprints the energy or abundance dissipation dynamics determined by the specific coordination environment. Generally, the phonon lifetime is proportional to its frequency[69] and the electron lifetime is inversely proportional to its bounding energy.[32] The skin high-frequency H–O or D–O phonons and the skin low-bound-energy electrons decay slowly than they do in the bulk.
Figure
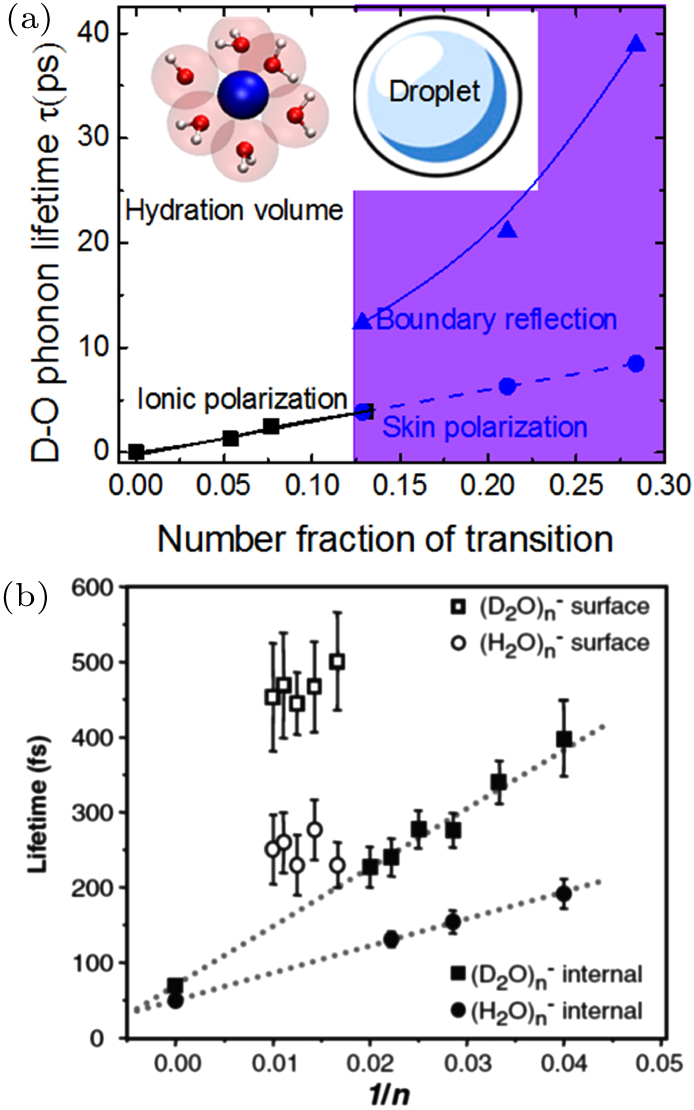 | Fig. 10. Ultrafast phonon and hydrated electron processes of water droplets.[32,33] Lifetime of (a) the D–O phonons in the droplet skin compared with that in the NaBr/H2O solutions[33] and the lifetime of (b) electron hydrated by the sized (H2O)n and (D2O)n clusters and their skins.[32] Insets in (a) illustrate the ionic hydration and the core-shelled water droplet. The skin supersolidity hinders the motion dynamics of both phonons and nonbonding electrons.[55] |
Figure 


One may extend the processes of photofluoresce[96] and very-low-energy electron diffraction by the complex surface potential barrier (SPB) to the ultrafast processes of electrons and phonons.[89] The SPB has two parts, V(r, E) = ReV(r) + iImV(r, E). The real elastic ReV part and imaginary inelastic ImV(r, E) part are correlated by Poisson’s equation ∇2ReV ∝ ρ (r) ∝ ImV(r, E), and –∇ReV ∝ ε (electric field). Interaction with the integral of the inelastic ImV(r, E) reduces the amplitude A of electron beam and interaction with the integral of the elastic ReV(r) shifts the phase φ of the electron waves traveling in the charge occupied region and its vicinity, ψ(r, t) ≈ A ei(kr – ω t + φ). The ImV(r, E) absorbs energy by activating secondary electrons. Likewise, the complex dielectric constant, 

The viscosity forms the imaginary part and the elasticity is the real part of the complex rheology for sliding friction[6] and phonon wave propagation. The local charge density of the pinned dipoles forms the ImV(r, E) and its image potential produces the ReV(r) for the hydronated electrons waves. In the skin, the high viscosity and charge density depress the respective wave amplitude by absorbing energy, which should shorten the lifetime of the traveling waves, instead. The longer lifetimes of electrons and phonons suggest that the high mechanical and electrostatic elasticity of the supersolid skin reflects waves to form quasi-standing waves with prolonged lifetimes. The higher the elasticity, the stronger reflectivity of the waves. Waves have similar amplitudes and wavelengths and moving in opposite directions could form a standing wave. The lifetime of an ideal standing wave is infinity. The longer electron lifetime of the (D2O)n clusters suggests their higher skin reflectivity or lower charge density. The isotope effect adds electron-phonon interaction as another degree of freedom.
—Low-frequency O:H phonon elastic adaptivity and dipolar repulsivity entitle skin mechanics[48]
Ice slipperiness means non-sticky and frictionless motion of a body sliding on ice, see Fig.
Mechanical detection suggests that the rheological skin of 102 nm thick has an elastic and a viscous component, which dictates the scratching friction.[6] At the atomic scale, Krim[97] proposed that interface lattice vibration and charge distribution play significant roles in sliding friction. Atomic vibration at a surface creates phonons with certain distinct frequencies. If the “plucking” action of atoms in the opposite surfaces of contacting motion, phonon resonance of both surfaces raises the friction coefficient, which explains why ice on ice has a higher friction coefficient.
Contrastingly, it was thought that an ice-like layer makes water skin tough, elastic, and hydrophobic, as confirmed using SFG spectroscopy and MD calculations.[100] A falling water droplet bounces rounds on water surface before it disappears, see Fig.
Computations[55] suggested that the skin stress and viscosity increase with the number reduction of its molecular layers. The stress increases from 31.5 mN/m to 73.6 mN/m when transiting a film from 15 to 5 layers of molecules, which approaches to the measured value of 72 mN/m for water skin at 298 K. The skin viscosity increases from 0.007 to 0.019 × 10−2 mN⋅s/m2, agreeing with the trend of measurements.[6] Theoretical reproduction of the stress thermal decay of water skin derived ΘDL = 192 K and EL = 0.095 eV.[47,101]
Does a liquid-like skin cover ice and an ice-like layer form on liquid? Results in Figs.
 | Fig. 11. Supersolid skin thermal stability.[57] Temperature dependence of (a) the full-frequency Raman spectra and (b) the frequency shift of the bulk, skin, and H–O dangling bond components. The H–O dangling bond undergoes thermal expansion (redshift) at T > 300 K. Both the bulk and the skin components undergo thermal contraction, at different slopes. At T > 340 K, the skin component turns to be thermal elongation, showing the O—O repulsive weakening. |
The counterpart of ice friction is always negatively charged regardless of the nature of its material because the undercoordination induced local polarization by the densely entrapped core electrons.[1] Such an elastic adaptive and repulsive contacting interface not only lowers the effective contacting force but also prevents charge from being transport between the counterparts. For ice on ice, O:H phonon resonance and interface fusing regelation raise the friction coefficient.[97] Therefore, the softer O:H phonon endows the elastic adaptivity and the nonbonding electron polarization ensures the hydrophobicity and repulsivity, making ice slippery and water skin tough. The skins and water and ice share the common gel-like supersolidity of elastic, viscus, less dense, repulsive, thermally stable.
—Heating can hardly shorten the undercoordination-shortened H–O bond further[57]
The full-frequency Raman spectra in Fig.
—O:H–O bond memory and skin supersolidity resolve the Mpemba’s heat transport dynamics[55]
One typical phenomenon in the fluid thermal transportation is the Mpemba effect, firstly noted by Aristotle in the 350 B.C. and asserted by, and named after, Mpemba in the 1960’s.[56] Under the same cooling condition, hot water cools faster than its cold though the successful observation is infrequent. This phenomenon has been attributed to convection, evaporation, impurity, supercooling, geometric structure, etc.
The Mpemba effect integrates the energy “heating absorption, cooling emission, cross-skin transportation, and source–drain interface dissipation” dynamics of liquid water.[55] One must consider these processes as a collection when dealing with this problem. Incorporating the skin supersolidity into the boundary and initial condition problem of Fourier fluid thermodynamics has reproduced the signatures of observations, see Fig.
 | Fig. 12. Skin thermal-diffusivity elevation and specific-heat depression.[102,55] Numerical reproduction of the measured (insets) initial-temperature dependence of (a) the θ (θi, t) decay and (b) the skin-bulk temperature difference Δθ (θi, t) of warm water. High skin thermal diffusivity due to density loss ensures the characteristic intersection. (b) The Δθ (θi, t) arises from the skin lower specific heat because heat flux conserves at the interface. |
Quantitative reproduction of the observed characteristics revealed four facts pertained to this phenomenon:
O:H–O bond memory. Only could the coupled O:H–O bond in liquid phase absorb energy by H–O heating contraction and emits energy by its inverse. The rate of energy emission is proportional to its initial storage, or the extent of H–O thermal contraction from its equilibrium, ΔEH ∝ (dH – dH0)2. The rate of energy emission, dEH/dt ∝ (dH – dH0)× ddH(θi, t)/dt, and, ddH(θi, t)/dt = [ddH(θi, t)/dθ (θi, t)]× [dθ (θi, t)/dt]. One can obtain the (ddH(θi, t)/dθ) from the ρ (θ) profile and the dθ (θi, t)/dt from equations in Fig. Skin high thermal diffusivity. Fourier equation of fluid thermodynamics has a term of thermal diffusion with the coefficient of α = κ/(ρ Cp) and a term of convection at 10−4 m/s velocity. The α is proportional to the thermal conductivity κ and inversely proportional to the mass density ρ and the constant-pressure specific-heat Cp. The cross point in Fig. Skin low specific heat. Because the thermal flux Q crossing the skin-core interface conserves, Q = (θ Cp)skin = (θ Cp)core ≥ 0, or, θskin/θcore = Cp,core/Cp,skin. The temperature difference, Δθ (θi, t) = θskin – θcore = θcore(Cp,core/Cp,skin – 1) ≥ 0, which yields Cp,skin < Cp,core, as it can be seen from Fig. Non-adiabatic heat dissipation. Improper source–drain interface conditions such as thermal insulation or a too large source volume will prevent the phenomenon from being take place. Other extrinsic factors such as evaporation, impurity, and supercooling play negligible roles for the Mpemba effect, as only thermal diffusivity and convention are involved in the Fourier fluid thermodynamics.
Mpemba effect can only be reproduced with involvement of the supersolid skin regardless of the presence of convection. O:H–O cooperative relaxation lowers the skin mass density and its specific-heat, which raises the thermal diffusivity to favor heat outflow from the liquid; the H–O thermal contraction absorbs energy; O:H–O memorability and recoverability ensures the unusual manner of heat emission. The Mpemba effect, or its inverse, should happen only to systems with involvement of strong coupling of the intermolecular bonding and intramolecular nonbonding lone pair interactions, which ensures the low mass density and high skin supersolidity, bond memory, and heating bond energy absorption. Contrastingly, most known materials have high skin mass density because of the atomic undercoordination induced bond contraction and the bond is subject to energy emission by thermal expansion, instead.[1]
—Supersolidity raises the viscoelasticity and the reactivity by polarization[76]
Nanobubbles (< 200 nm in diameter) can form easily by dissolving gases like argon, hydrogen, nitrogen, oxygen, and methane in bulk water.[10] According to the classical view of the air–water interface, such bubbles should not exist at all. The small radius of curvature implies a high Laplace pressure inside the bubble that should drive gas diffusion across the interface and cause the bubbles to dissolve almost instantly.[103] However, nanobubbles have peculiar properties such as long lifetime and high gas solubility owing to their negatively charged surface and high internal pressure.[93] Being stable for days or even for months than classical theory can predict, nanobubbles are used in fields such as diagnostic aids, drug delivery, water treatment, biomedical engineering, degradation of toxic compounds, water disinfection, and cleaning of solid surfaces including membrane.[104]
The unexpected stability was thought an awkward but conspicuous instance of “surface mis-behavior”. The liquid/gas interface resists mass diffusion. Theoretical investigation[60] suggests that the limited gas diffusion and the pinned contact line of the nanobubbles lead to the slow dissolution rate.
A bubble is just the inversion of a droplet. A hollow sphere like a soap bubble contains the inner and the outer skins of different curvatures.[105] Both skins are in the supersolid state and the volume fraction of such supersolid phase over the entire liquid-shell volume is much greater than simply a droplet. Nanobubble and nanodroplet have high skin curvatures, ±1/K. The effective molecular CN varies with the skin curvature, zcluster < zdroplet < zflat < zcavity < zbulk = 4. The geometrical configuration of the skin molecules stays the bulk attribute, but the length and energy vary with the CN loss — smaller molecular size but larger separation. The fraction of supersolid molecules increases with the curvature. For a sufficiently small water droplet or a bubble, the volume of the skin and the volume of the core is compatible, they hold a bi-phase structure of low-density skin and high-density core of the same tetrahedral structure. If the structure is sufficiently small the skin supersolidity becomes dominant. So, the extent of supersolidity becomes more pronounced as the droplet size is reduced.
Therefore, bubbles show more significantly the supersolidity nature – elastic, hydrophobic, and less dense, which makes bubbles mechanically stronger, chemically more active, and thermally more stable. The strong skin polarization prevents gas diffusion across the skin of the bubble. The supersolidity is a notion that appeals to old ideas about hydrophobic particles creating a highly ordered and ice-like hydration shell in aqueous solution.
The intrinsic behavior of the O:H–O between the undercoordinated molecules is the key controlling the performance of small bubbles. The skin supersolidity stems the unusual thermal and mechanical stability of the curved surfaces. Therefore, nanoscale water ice is more elastic, hydrophobic, repulsive, and less dense with even lower TN and TV and higher Tm. Figure
 | Fig. 13. Nano-supersolid TN depression – supercooling.[48,53] Skin supersolidity takes the full responsibility for (a) water skin toughness, ice slipperiness, and (b) droplet-size and surface-curvature (inset) resolved TN depression (called supercooling).[106,112] Droplet of slightly more-curved surface freezes 68.4 s later at 269 K than the contrast deposited on smooth Ag surface.[111] |
Molecular undercoordination raises the Tm for a monolayer to 325 K[109] and the skin of bulk water to 310 K.[53] Raman spectroscopy examination of water inside single-walled carbon nanotubes (SWCNT) revealed larger Tm elevation (by as much as 100 °C).[110] The Tm is bracketed to 105–151 °C for a SWCNT of 1.05 nm across and 87–117 °C for a 1.06 nm SWCNT. Phase changes for the 1.44 nm and 1.52 nm SWCNTs occur between 15–49 °C and 3–30 °C, respectively. In contrast, the TN for the 1.15 nm SWCNT is between –35 °C and 10 °C.
Figure
Supercooling, also known as undercooling, is the process of lowering the temperature of a liquid below its TN without it becoming a solid or cooling a gas below TN without turning into liquid. Once the supercooled water is disturbed with a slapping impulse, it soon becomes “instant ice”. Supercooled water occurs in the form of small droplets in clouds and plays a key role in the processing of solar and terrestrial radiative energy fluxes. Supercooled water is also important for life at subfreezing conditions for the cryopreservation of living cells, and for the prevention of hydrate formation in nature gas pipelines. Superheating is the opposite. Once the superheated water is disturbed by adding impurity such as sugar, the superheated water will explode.
—Electrostatic repulsivity and mechanical elasticity foster the interface superfluidity[48]
Superfluidity of water droplet transporting in a hydrophobic channel is of great importance to many subject areas such as cell culturing. An air gap of 0.5–1.0 nm thick exists between the channel wall and the fluid[113] because of the electrostatic repulsion between the counter parts at relative motion. For the hydrophobic contact, the water has a 3.8 Å thick skin of 0.71 g/cm3 mass density and there is a 0.6 nm hydrophobic gap between the liquid and the SiO2 support.[114] The presence of a h = 0.6 nm thin vapor (low density) layer separating water and the hydrophobic surface makes the nanoscaled water travelling through the channel much faster than the fluid theory can predict,[19] see Fig.
The hydrophobicity, superfluidity, superlubricity, and supersolidity (extended from 4He solid) (called 4S) share the same mechanism – elastic, repulsive, and frictionless at motion. Wenzel–Cassie–Baxter’s law suggests that nanoscaled roughening makes a hydrophobic surface even more hydrophobic and a hydrophilic surface more hydrophilic.
It is recommended that the fluid skin has a double layer of charge separation without knowing how the double layer is formed.[115] From the BOLS-NEP point of view, the skin H–O contraction and the dual process of polarization endows the surface with excessive electrons in the form of dipoles. Therefore, the 4S is readily attributed to the high elasticity and the repulsivity of skin dipoles at the contacting interfaces. Particularly, the hydrophobic–hydrophilic cycling transition by an UV excitation or plasma radiation evidences the removal and recovery of the solid surface dipoles. For a solid surface of entrapment dominance, the roughening raises the apex curvature and hence enhances the hydrophobicity or hydrophilicity.
—Bonding and electronic dynamics could promisingly lead to the core science of water ice[89]
To summary, molecular undercoordination matters the performance of low-dimensional water ice by creating a supersolid phase through O:H–O bond cooperative relaxation, O 1s binding electron entrapment, nonbonding lone pair polarization, and specific-heat dispersion. Water prefers the ordered, tetrahedrally-coordinated, fluctuating structure covered with a supersolid skin. O:H–O performs as an asymmetrical, coupled oscillator pair. The cooperativity and the segmental specific-heat disparity of the O:H–O dictate the extraordinary adaptivity, recoverability, sensitivity of water and ice when subjecting to a perturbation.
The O:H–O specific-heat disparity results in the vapor, liquid, QS, ice Ih and Ic, and XI phases of mass density oscillation. The QS phase of negative thermal expansion transits the density from maximum to minimum and defines the critical temperatures of melting Tm, evaporating TV, and ice nucleation TN. Molecular undercoordination raises the Tm and lowers the TV and TN by outward shifting the QS boundary though Einstein’s relation ΘDx ∝ ωx, which results in the observed supercooling at freezing and evaporating and superheating at melting of the nanometer sized water.
The polarization creates a supersolid skin phase that is hydrophobic, viscoelastic, and frictionless. The supersolid skin of ice and liquid share the common H–O stiffness of 3450 cm−1 characteristics, which limits the energy dissipation dynamics of the hydrated electrons and high-frequency H–O phonons. The highly elastic adaptivity of the O:H and the surface electrostatic repulsivity stem the ice slipperiness, water skin toughness, and the superfluidity of water droplet traveling in hydrophobic channels. Raising a surface curvature enhances the supersolidity and widens the temperature range of supersolidity, which raises the skin reactivity and stabilizes droplet and bubble in mechanical strength and thermal durability of droplets and bubbles. Reproduction of the Mpemba paradox – warm water cooling more quickly, evidences for the skin high thermal diffusivity and lower specific-heat.
Progress demonstrated the efficiency and essentiality of the rules and the concepts, particularly, the BOLS-NEP and coupled O:H–O bond theories, in dealing with low-dimensional water ice, which opened the door and paved the path directing to the core chemistry and physics of water and ice. Thinking about water ice and other molecular crystals from the perspective of coupling inter- and intramolecular bonding and electronic dynamics would be even more challenging, fascinating, promising, and rewarding.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] | |
| [39] | |
| [40] | |
| [41] | |
| [42] | |
| [43] | |
| [44] | |
| [45] | |
| [46] | |
| [47] | |
| [48] | |
| [49] | |
| [50] | |
| [51] | |
| [52] | |
| [53] | |
| [54] | |
| [55] | |
| [56] | |
| [57] | |
| [58] | |
| [59] | |
| [60] | |
| [61] | |
| [62] | |
| [63] | |
| [64] | |
| [65] | |
| [66] | |
| [67] | |
| [68] | |
| [69] | |
| [70] | |
| [71] | |
| [72] | |
| [73] | |
| [74] | |
| [75] | |
| [76] | |
| [77] | |
| [78] | |
| [79] | |
| [80] | |
| [81] | |
| [82] | |
| [83] | |
| [84] | |
| [85] | |
| [86] | |
| [87] | |
| [88] | |
| [89] | |
| [90] | |
| [91] | |
| [92] | |
| [93] | |
| [94] | |
| [95] | |
| [96] | |
| [97] | |
| [98] | |
| [99] | |
| [100] | |
| [101] | |
| [102] | |
| [103] | |
| [104] | |
| [105] | |
| [106] | |
| [107] | |
| [108] | |
| [109] | |
| [110] | |
| [111] | |
| [112] | |
| [113] | |
| [114] | |
| [115] |


