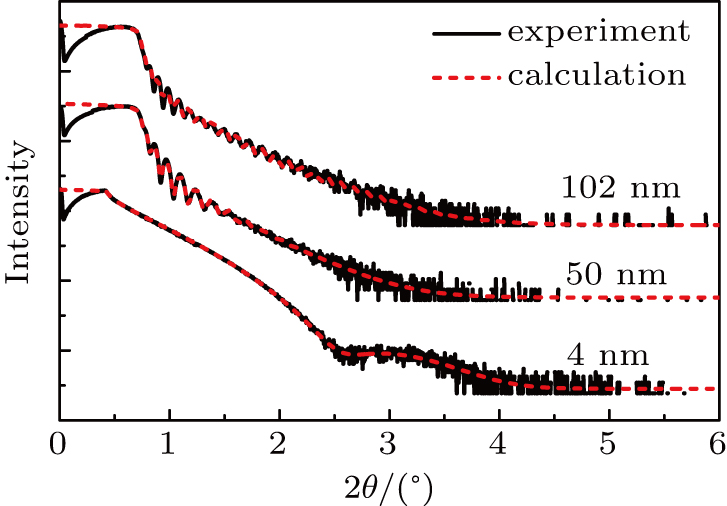
The XRD pattern measured for orientation analysis of the NbN thin film is given in Fig. 1. The result shows that the (111) diffraction peak is from the NbN thin film and (100) is from the silicon (Si) substrate. The film thickness was determined by XRR measurements and the results are presented in Fig. 2. The XRR results for different thickness NbN films with about 0.5 nm surface roughness were deduced from a multilayer model by fitting the XRR data.

Fig. 1.

	Figure Option ViewDownloadNew Window
	Fig. 1. XRD characterization of NbN 100 nm thin film.

Fig. 2.

	Figure Option ViewDownloadNew Window
	Fig. 2. XRR measurements were performed on NbN films of given thicknesses. Experimental results (black solid line) of the specimens were fitted (red short dash) by a multilayer model from bottom to top with the fitted NbN thicknesses shown.

The resistive transition curves under zero magnetic field for different thickness micro-bridges measured from 2 K to 300 K are illustrated in Fig. 3(a). The results show that superconducting transition temperature T_c decreases with decreasing thickness and the thickness dependence of T_c is shown in Fig. 3(b).

Fig. 3.

	Figure Option ViewDownloadNew Window
	Fig. 3. (a) Normalization of resistance as a function of temperature curves for different micro-bridges at zero fields. Inset: R–T is measured from 2 K to 300 K. (b) Thickness dependence of the transition temperature. The black solid symbols are experimental data and the red solid line is to guide the eyes.

The suppression of T_c with decreasing thickness in the superconducting films is in agreement with previous reports.^{[10,17, 22–25]} This fall of T_c is a dimensional crossover phenomenon driven by the strength of the order parameter fluctuations, which increases with reduced dimensionality.^[26]

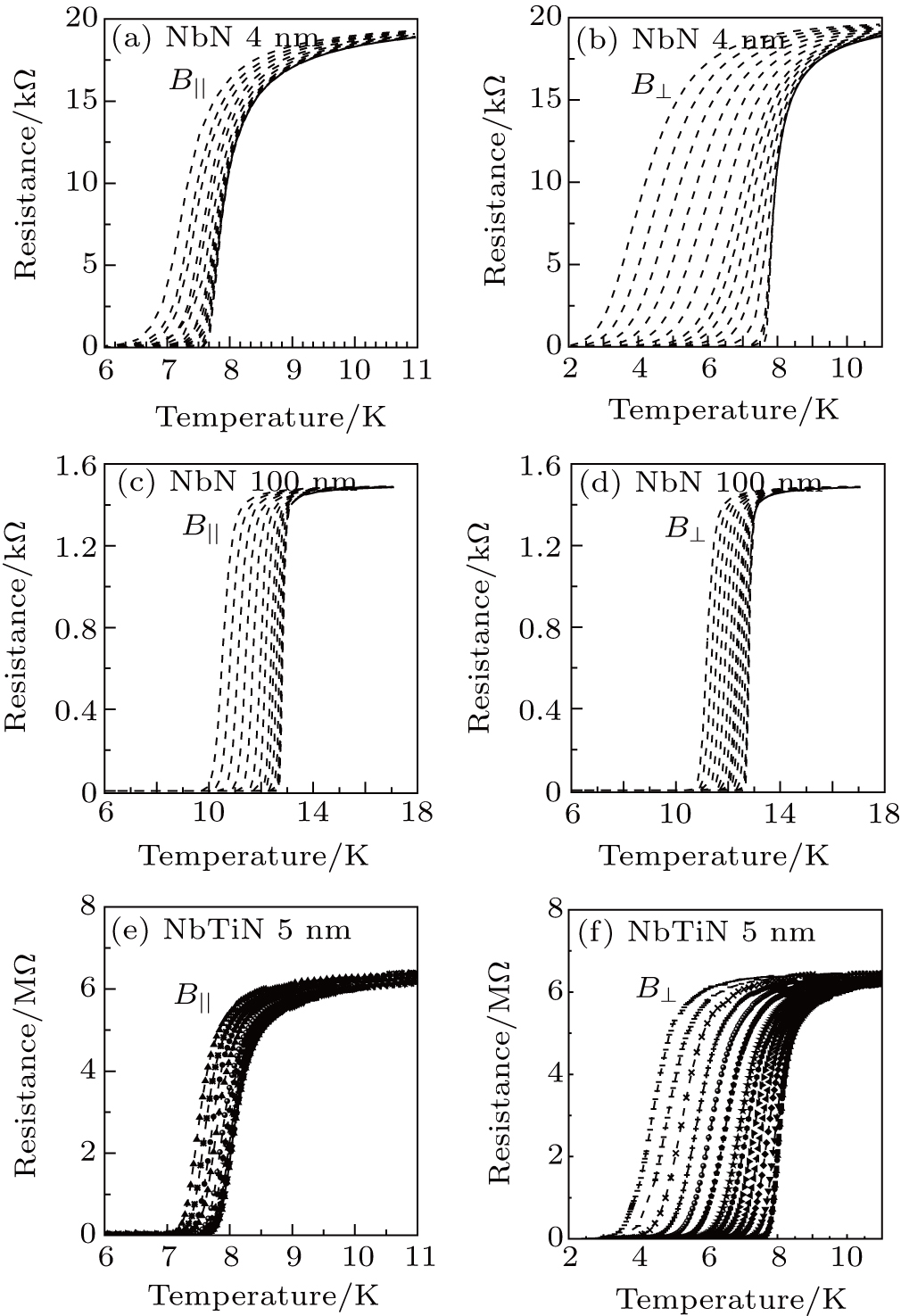
Resistive transition R (T, H) curves under different applied magnetic fields in both the parallel and perpendicular orientations of the superconducting specimens are displayed in Fig. 4 for three samples. As expected, the transition curves shift towards lower temperature with increasing magnetic field apparently, which do not broaden significantly in both parallel and perpendicular directions for the all given samples. To evaluate the superconducting behavior, we analyze the temperature dependence of the upper critical field for different thickness specimens. The upper critical field H_c2 is defined at half of the residual resistance (R_{15 K} = residual resistance), the data are shown in Fig. 5 for three NbN samples and one NbTiN sample, respectively.

Fig. 4.

	Figure Option ViewDownloadNew Window
	Fig. 4. The R–T curves measured in different applied magnetic fields 0, 0.05, 0.1, 0.5, 1, 1.5, 2, 2.5, 3, 3.5, 4, 4.5, 5, 6, 7, 8, 9 (right to left, in units of T) for given specimens in both parallel and perpendicular orientations. By increasing the field, all curves move towards lower temperatures apparently and do not broaden.

Fig. 5.

Figure Option ViewDownloadNew Window

Fig. 5. The temperature dependent parallel and perpendicular upper critical field diagrams. (a) The upper critical field for ultra thin 4 nm film and NbTiN 5 nm nanowire. The Hc2∥(t) shows pronounced 2D behavior and is well fitted with 2D GL Eq. (1) as indicated by the blue dash line. The black open circles and red open squares represent Hc2∥(t) for 4 nm NbN film and NbTiN 5 nm wire, respectively, and the Hc2∥(t) dependence shows a similar behavior. The solid triangles illustrate the Hc2⊥(t) data for NbN 4 nm film. (b), (c) The parallel critical field decreases while the perpendicular upper critical field rises with increasing thickness and the bending curvature moves towards Tc. The Hc2∥(t) is explained with AGL interpolation crossover Eq. (2) and the perpendicular upper critical field data exhibit a linear behavior and are well fitted with Eq. (3). The arrows show tcr crossover temperature, and Hc2(t) shows crisscross in high thickness samples. The open circles and solid triangles represent parallel and perpendicular field experimental data, respectively, and are fitted using Eqs. (2) and (3) as shown by the red and green solid lines.

From these results, several features of H_c2(t) could be identified. Firstly, all samples show clearly anisotropy in the upper critical field. In other words, the difference between H_c2⊥(t) and H_c2∥(t) is substantial. Secondly, the H_c2∥(t) curves show upturn bent curvatures, especially at temperatures close to T_c. This feature is more pronounced for the ultra-thin samples. In contrast, the H_c2⊥(t) curves show mostly linear behavior, except for the very thin ones. Thirdly, for the two thicker samples (50 nm and 100 nm), the H_c2⊥(t) and H_c2∥(t) curves show crisscross as exhibited in Figs. 5(b) and 5(c).

We first discuss the bent curvature of H_c2∥(t) for samples with different thicknesses. This kind of feature has been widely observed in ultra-thin superconducting films^{[20, 27–31]} and is explained by the 2D nature of the films when the film thickness becomes smaller than the superconducting coherence length of the material.^[32] Harper and Tinkham have solved the linearized Ginzburg–Landau equation under the limit d ≪ ξ^[33] and obtained

As d starts to increase and becomes comparable or even larger than the coherence length d > ξ, the system undergoes a crossover to a 3D linear region, which is clearly observed for the thick film samples. Schneider and Locquet have investigated crossover using the linearized AGL theory^[26] and obtained an expression for a large temperature region that covers the crossover

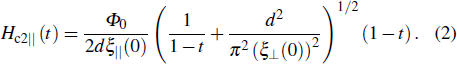
The temperature dependence of the perpendicular upper critical field H_c2⊥ shows a linear behavior for the thick samples as predicated by the Ginzburg–Landau theory. However, we note that the ultra-thin samples and the NbTiN nanowire sample show slightly upturn curvatures in H_c2⊥(t). The somewhat unexpected results will be discussed in Subsection 3.4.

The linear temperature dependence of the perpendicular upper critical field is given^[26] as

Table 1.

Table 1.

Table 1. The parameters, coherence lengths, and Tc defined at half of residual resistance for given samples. . Sample Tc/K ξ∥(0)/nm ξ⊥(0)/nm NbTiN 5 nm wire 8.1 6.46 NbN 4 nm 7.9 8.6 NbN 50 nm 12.42 2 5 NbN 100 nm 12.83 2.14 7

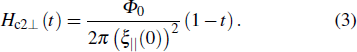
Table 1. The parameters, coherence lengths, and Tc defined at half of residual resistance for given samples. .

Interestingly, the temperature dependence of the perpendicular upper critical field exhibits a bending curvature very close to T_c in ultra thin NbN and NbTiN meander nanowire samples as shown in Fig. 6. This behavior was also reported previously.^{[20, 28, 30]} In Ref. [24], it was suggested that the observed upturn bending in Nb meander nanowire samples could be due to the dimensional crossover effect when the coherence length ξ_∥ becomes larger than the width of the nanowire samples. Although this is a possible scenario because the coherence length diverges at T_c, it should only appear at a temperature region very close to T_c. Further, in this case of study, the width of the NbN samples is 20 μm that suggests the dimensional crossover effect can hardly be seen. Alternatively, Nam et al. have investigated the critical field of a superconducting nanomesh network.^[20] They found a similar upturn curvature in the temperature dependence of the perpendicular critical field for the samples which were not fully covered by superconducting grains while a linear behavior was observed for the fully covered ultra-thin film samples. They suggested that the local variation in T_c led to suppression of pair-breaking and, hence, enhanced the critical field near T_c.

Fig. 6.

	Figure Option ViewDownloadNew Window
	Fig. 6. Temperature dependence of the perpendicular upper critical field results for the ultra-thin NbN and the NbTiN nanowire samples. Bending curvature close to Tc is observed and the red solid lines are the fitted curves using a (1−t)γ relation.

We may use this model to explain our H_c2⊥ data for the ultra-thin samples. In these samples, there could be a local small variation in T_c. Furthermore, when we compare the 4 nm NbN sample to the NbTiN nanowire sample, we note that the former shows more clear upturn curvature in H_c2∥(t). This indicates that the 4 nm NbN sample may have larger local variation in T_c than the NbTiN nanowire sample, being in agreement with the in-field transition data measured on the two samples, as shown in Figs. 4(b) and 6(a).

Empirically, we could fit the H_c2⊥(t) data using (1−t)^γ relation with γ as a fitting parameter. The perpendicular upper critical field data is fitted and indicated with a red solid line in Figs. 6(a) and 6(b) for the ultra thin NbN and NbTiN nanowire samples, the best fits give γ = 0.8 and 0.9 for these two samples, respectively.

Based on the results, we propose that we may use the temperature dependence of H_c2⊥ as a measure of uniformity of superconducting ultra-thin films. In other words, a linear behavior of H_c2⊥(t) could be an indication of better quality for ultra-thin samples.

In order to clarify the 2D behavior of the 4 nm thin NbN film and 5 nm thick NbTiN nanowire samples, angular dependent upper critical field measurements were performed on these two samples. The measurements were carried out at fixed temperatures close to T_c and at different angles by sweeping the magnetic field up to 9 T. The results are shown in Figs. 7(a) and 7(b), where θ is the angle between the normal of the sample plane and the direction of the applied magnetic field. The angles 0° and 90° are defined as perpendicular and parallel directions to the surface of the samples. We choose the upper critical field at half of the residual resistance and draw H_c2 vs. θ graph. The results are presented in Figs. 7(c) and 7(d).

Fig. 7.

Figure Option ViewDownloadNew Window

Fig. 7. Superconducting resistive transition curves under applied magnetic field 0 up to 9 T at different angles for (a) NbN 4 nm at temperature 7.8 K and (b) NbTiN 5 nm at 7.8 K. The upper critical field is defined at half of residual resistance and its angular dependence is shown for (c) NbN 4 nm and (d) NbTiN 5 nm nanowire. The sharp peak is seen at θ = 90° for given samples which is fitted with the 2D Tinkham and 3D anisotropic formulas given in Eqs. (4) and (5) as indicated by the red and blue solid lines, respectively. The black circles represent the experimental data. The inset shows a zoom-in view of the region around θ = 90°.

It is well known that a 2D superconductor and an anisotropic 3D superconductor show different angular dependences of H_c2.^[37–39] In the 2D case, H_c2 (θ) follows the 2D Tinkham model given as

In our samples, a cusp like peak is clearly observed at θ = 90° where the external magnetic field is aligned in parallel to the sample surface, as shown in Fig. 7. The red and blue solid lines represent fitting results using Eqs. (4) and (5) for 2D and 3D systems, respectively. These results suggest that the ultra-thin NbN and NbTiN nanowire samples are in the 2D regime as we have discussed in Subsection 3.3.

As shown in Fig. 5(c), the parallel and perpendicular upper critical field curves of the 100 nm NbN sample crisscross each other at a certain temperature. Below the crisscross, H_c2∥ is higher than H_c2⊥ and above the crisscross point at low temperature, it exhibits the opposite behavior. The similar behavior is also observed for the NbN 50 nm sample. Interestingly, the crisscross is found to shift toward T_c with increasing thickness. This shift of crisscross can be understood by considering the much reduced 2D region in the thicker sample.

The existence of the crisscross also indicates that H_c2⊥ would show maxima in the angular dependence of the upper critical field. In Fig. 8(a), we present data for the 100 nm sample. Indeed, the upper critical field not only shows a peak in the parallel orientation, but also exhibits maxima in the perpendicular direction. In this case, H_c2⊥ is even higher than H_c2∥.

Fig. 8.

Figure Option ViewDownloadNew Window

Fig. 8. (a) Angular dependence of upper critical field graph for NbN 100 nm is taken at temperature 11.25 K. The upper critical field shows maxima for both parallel and perpendicular orientations. The Hc2 peak for the perpendicular orientation is believed to be due to the columnar structures formed during the growth of the thick films. (b) TEM image clearly shows columnar in NbN 100 nm film. The top, middle, and bottom layers represent the substrate, film, and protection layer, respectively. The red arrow indicates the one typical columnar structure.

The existence of the crisscross also indicates that H_c2⊥ would show maxima in the angular dependence of the upper critical field. In Fig. 8(a), we present data for the 100 nm sample. Indeed, the upper critical field not only shows a peak in the parallel orientation, but also exhibits maxima in the perpendicular direction. In this case, H_c2⊥ is even higher than H_c2∥.

The enhanced upper critical field in the perpendicular direction has been reported before in NbN films and is related to the columnar structures formed during the film growth.^[35] We checked microstructure of the 100 nm sample using the transmission electron microscopy (TEM), the results are shown in Fig. 8(b). From the TEM micrographs, columnar-like structures along the direction normal to the sample surface can be seen clearly with a typical size around 5 nm. The presence of the columnar structures could reduce the mean free path and, thus, reduce the effective in-plane coherence length, leading to enhancement of H_c2⊥.

To further investigate the anisotropic properties of the samples, we carried out angular dependent magneto-resistance measurements at different temperatures and at fixed field 5 T. During the measurement, the sample was rotated along the axis perpendicular to the magnetic field and the current was also applied in the rotating axis direction. The results are shown in Fig. 9 for two samples, 4 nm and 100 nm NbN films. The angular dependence of the magneto-resistance is also obtained for the NbTiN nanowire sample, and the result is similar to that of the 4 nm NbN sample. The anisotropic magneto resistance (AMR) is observed. Within a full rotation, two minima appear in the AMR data of the 4 nm NbN sample and four minima are observed for the thick 100 nm NbN sample. Bearing in mind that the angular dependence of the magneto-resistance is controlled by the angular variation of H_c2, the results are consistent with the previous temperature and angular dependent upper critical field data. The extra minima observed in the 100 nm sample are due to the columnar structure, as we discussed in the previous subsection.

Fig. 9.

	Figure Option ViewDownloadNew Window
	Fig. 9. (a), (c) Angular variation of the resistance for NbN 4 nm thin and 100 nm thick films at fixed applied field for different temperatures. (b), (d) Polar plot of magneto-resistance is observed folding symmetry.