† Corresponding author. E-mail:
Project supported by the National Natural Science of China (Grant Nos. 41527804 and 41774169), the Strategic Priority Research Program of the Chinese Academy of Sciences (Grant No. XDB 41000000), and the Key Research Program of Frontier Sciences of the Chinese Academy of Sciences (Grant No. QYZDJSSW-DQC010).
Reconnection electric field is a key element of magnetic reconnection. It quantifies the change of magnetic topology and the dissipation of magnetic energy. In this work, two-dimensional (2D) particle-in-cell (PIC) simulations are performed to study the growth of the reconnection electric field in the electron diffusion region (EDR) during magnetic reconnection with a guide field. At first, a seed electric field is produced due to the excitation of the tearing-mode instability. Then, the reconnection electric field in the EDR, which is dominated by the electron pressure tensor term, suffers a spontaneous growth stage and grows exponentially until it saturates. A theoretical model is also proposed to explain such a kind of growth. The reconnection electric field in the EDR is found to be directly proportional to the electron outflow speed. The time derivative of electron outflow speed is proportional to the reconnection electric field in the EDR because the outflow is formed after the inflow electrons are accelerated by the reconnection electric field in the EDR and then directed away along the outflow direction. This kind of reinforcing process at last leads to the exponential growth of the reconnection electric field in the EDR.
Magnetic reconnection provides a mechanism for mass transport and energy conversion in many plasma physical settings. It is generally considered to be responsible for solar flares[1] and coronal mass ejections[2] in the solar atmosphere, substorms in the earth’s magnetotail,[3–6] injections of the solar wind mass and energy into the earth’s magnetopause,[7,8] and disruptions in the laboratory experiments.[9,10] In these plasma environments, the mean free path of charged particles is usually very large; thus the classical Coulomb collision is negligible. A collisionless reconnection model is believed to be suitable in these plasma systems.[11,12]
The reconnection electric field plays a pivotal role in both energy conversion and production of energetic particles during magnetic reconnection by doing work on particles.[13–17] In steady-state reconnection, the normalized reconnection electric field can be employed to represent the reconnection rate, and it is equivalent to the ratio of the inflow speed to the Alfvén speed. In collisionless magnetic reconnection, the diffusion region has two layers: the ion diffusion region and the electron diffusion region. In the electron diffusion region (EDR), both electrons and ions are unmagnetized, and electrons become magnetized in the ion diffusion region. The reconnection rate in collisionless magnetic reconnection is mediated by the Hall effect resulting from such a kind of decoupled motions between ions and electrons, and the reconnection rate is around 0.1. Correspondingly, the reconnection electric field is about 0.1vAB0, where vA is the Alfvén speed, and B0 is the upstream magnetic field.[11,18] However, in reality, magnetic reconnection is non-stationary and the reconnection electric field is time evolutionary. The evolution of the reconnection electric field has three stages. A seed electric field is firstly produced in the current sheet, and then it grows until a maximum value is attained; finally its evolution saturates. The seed electric field can be generated by instabilities in the current sheet, such as the tearing-mode instability,[19–21] lower hybrid drift instability,[22,23] Buneman instability,[24,25] and Kelvin–Helmholtz instability.[26] In simulations of magnetic reconnection, the seed electric field is usually provided by an initial perturbation in order to bypass the linear growth of instabilities in the current sheet and forces the system into the reconnection stage, where the reconnection electric field grows spontaneously, from the beginning of the simulations.[11,13,27] When the initial perturbation is sufficiently small, it will not change the following evolution of the reconnection electric field.[11]
Litvinenko[28] studied steady magnetic reconnection in the framework of incompressible Hall magnetohydrodynamics, they find that the Hall effect plays an important role in the reconnection rate enhancement and the current sheet thinning, and obtain an analytical relation between the reconnection electric field and the outflow speed. In collisionless magnetic reconnection, the reconnection electric field in the EDR is dominated by the divergence of the electron pressure tensor.[21,27] Hesse[29] further found that the reconnection electric field in the EDR is related to the gradient of the electron bulk velocity. However, so far, there were very few studies on the spontaneous growth of the reconnection electric field from the seed electric field in magnetic reconnection. Lu et al.[21] developed a theoretical model to explain the self-reinforcing process of the reconnection electric field in the EDR during anti-parallel magnetic reconnection. In the model, they proposed that the reconnection electric field is proportional to the electron outflow speed, while the electrons obtain their outflow speed from the acceleration by the reconnection electric field in the EDR. Such a self-reinforcing process leads to exponential growth of the reconnection electric field, which was further verified by two-dimensional (2D) particle-in-cell (PIC) simulations. Compared with anti-parallel reconnection, the more general case is guide filed reconnection, where the shear angle between the reconnecting magnetic field cross the current sheet is less than 180°.[30] Previous studies indicated that the reconnection rate in guide field reconnection is only a little smaller than that in anti-parallel reconnection. However, the tearing-mode instability in the current sheet with a guide field and the structure of the diffusion region in guide field reconnection are greatly different from the anti-parallel case.[27,31] Therefore, in the present paper we will investigate the spontaneous growth of the reconnection electric field in the EDR during guide field reconnection.
In this section, 2D PIC simulations are performed to investigate the evolution of the reconnection electric field during magnetic reconnection with a guide field. The simulation code has been successfully used to study magnetic reconnection and plasma waves.[13,32–36] The simulations are conducted in the x–z plane, and the initial condition is the Harris-type current sheet with the magnetic field B(z) = B0tanh(z/δ) ex – Bg ey, where Bg = B0 is a uniform guide field. The density profile is n(z) = n0sech2(z/δ) + nb, where nb = 0.2n0 is the background plasma density. The half width of the current sheet is δ = 0.5di, where di is the ion inertial length based on n0. The initial velocity distributions of ions and electrons are assumed to be Maxwellian with the temperature ratio Ti/Te = 4, and the ion-to-electron mass ratio is set to be mi/me = 64. The speed of light is assumed to be c/vA = 15, where vA is the Alfvén speed based on B0 and n0. The simulation domain is [–Lx, Lx] × [–Lz, Lz] with spatial resolution Δ x = Δ z = 0.025di, where Lx = 30di and Lz = 7.5di. The time step is 
In the first case, we do not add any initial perturbation, or Ψ0 = 0. The process of magnetic reconnection is clearly demonstrated in Fig.
 | Fig. 1. (a) Time evolution of the magnetic flux function Ψ/(B0di) along z = 0. (b) Time evolution of |ΨM| with M = 5–9. In this case, there is no initial perturbation. |
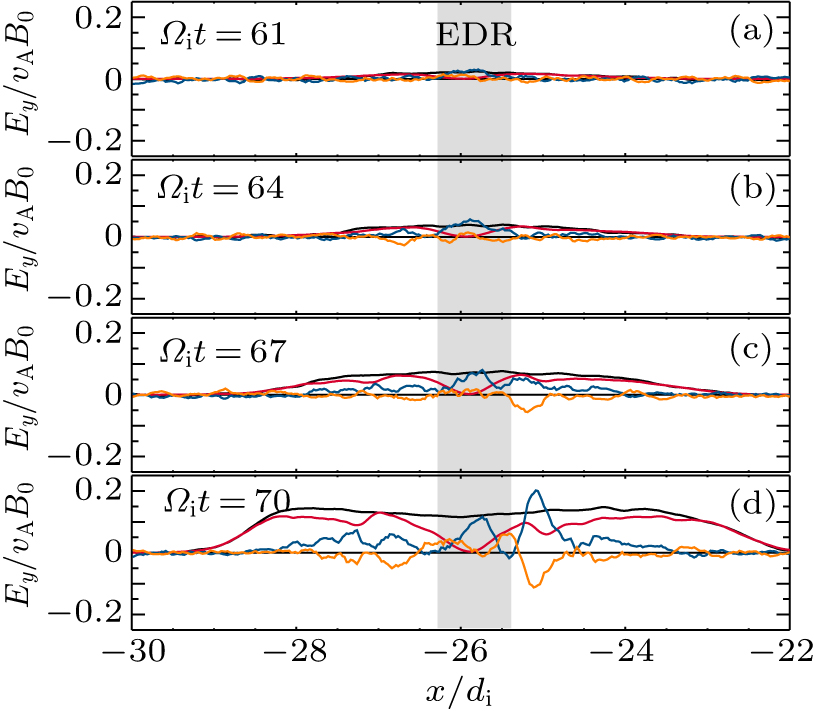
In this paper, we focus on the spontaneous growth of the reconnection electric field after reconnection onset occurs. Figure
Using the electron momentum equation, one can easily find that the electric field can be expressed as

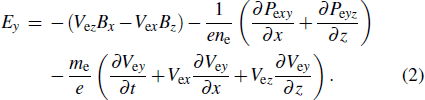
After knowing the position and velocity of each particle, we can easily calculate the electron bulk velocity and electron pressure tensor. At last, we obtain the electron convection term, electron pressure tensor term, and electron inertial term as described in Eq. (
In general, the reconnection electric field at the X line is used to quantify the topological change of magnetic field lines, and it is also related to the conversion of magnetic energy into plasma kinetic energy and the production of energetic particles. Therefore, in this paper, we focus on the evolution of the reconnection electric field at the X line, or its self-reinforcing process, during magnetic reconnection. Figure
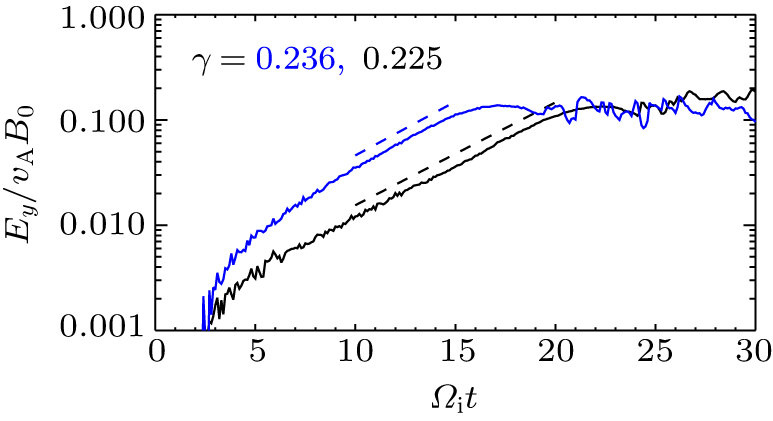
 | Fig. 4. Time evolution of the out-of-plane electric field Ey / vAB0 in the EDR. The dashed line shows the fitted exponential growth rate. In this case, there is no initial perturbation. |
We also run two cases with initial perturbations, whose amplitudes of the magnetic flux are Ψ0 / (B0di) = 0.05 and 0.1, respectively. The evolution of the reconnection electric field Ey at the X line in these simulations is plotted in Fig.
A theoretical model is proposed in this section to describe the spontaneous growth of the reconnection electric field in the EDR during guide field reconnection. From the simulation, we see that the reconnection electric field around the X line is mainly balanced by the electron pressure tensor term, and it can be expressed as[29]
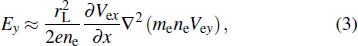
Figure

 | Fig. 6. A sketch of the electron diffusion region.[21] |
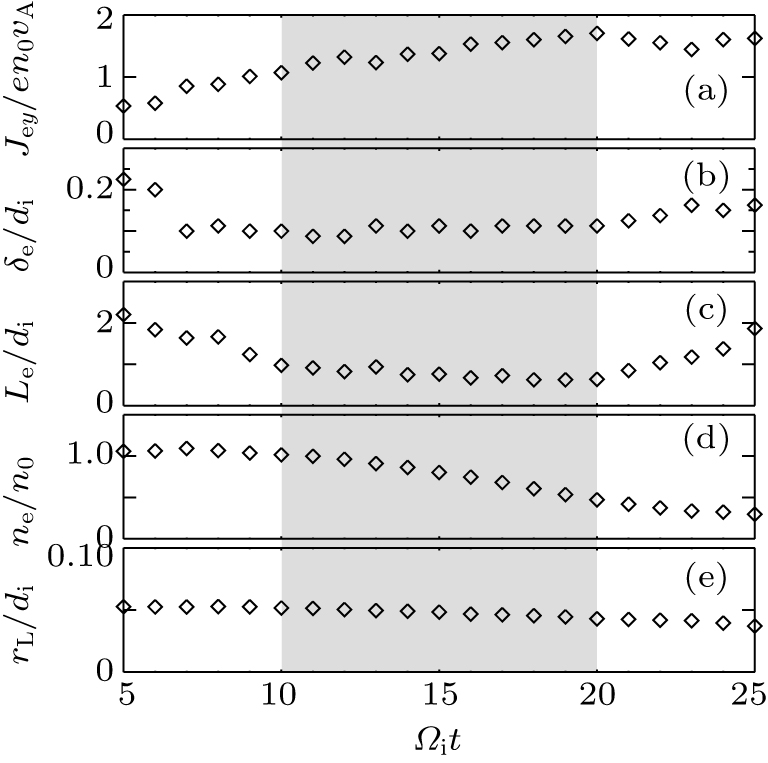
If we assume that the EDR is stationary during the spontaneous growth of the reconnection electric field, the parameters Jey, δe, Le, ne, and rL are kept as constants. Then, from Eq. (

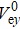

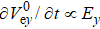



In our theoretical model, we assume that the half length and width of the EDR Le and δe, as well as the electron current density in the y direction Jey, electron density ne, and electron Larmor radius in the guide field rL in the EDR are unchanged. Based on the simulations described in Section 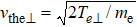
To examine the robustness of the theoretical model, we vary the amplitude of the guide field to Bg / B0 = 1, 2, and 3. The other parameters are kept fixed as those described in Section
In this paper, based on both 2D PIC simulations and a proposed theoretical model, we have investigated the spontaneous growth of the reconnection electric field in the EDR during magnetic reconnection with a guide field. The reconnection electric field in the EDR is dominated by the electron pressure tensor term, while it is found to be directly proportional to the electron outflow speed. The time derivative of electron outflow speed is proportional to the reconnection electric field in the EDR because the outflow is formed after the inflow electrons are accelerated by the reconnection electric field in the EDR and directed away along the outflow direction. This kind of reinforcing process at last leads to the exponential growth of the reconnection electric field in the EDR. In this paper, we do not consider the influence of secondary islands which may be formed in the EDR during the evolution of magnetic reconnection on the spontaneous growth of the reconnection electric field, and this is our future plan.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] |