† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant No. 11672094).
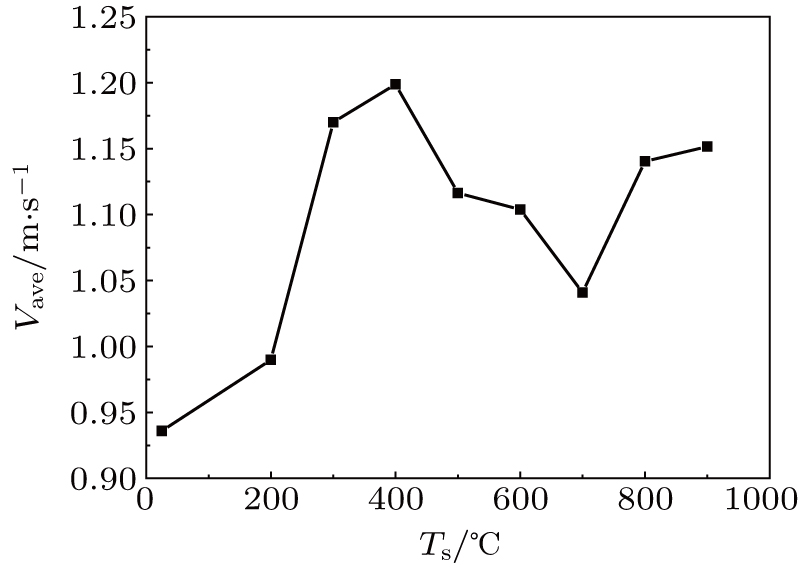
We experimentally investigate the drag reduction characteristics of heated spheres falling into water by using a high-speed camera. In 25-°C water, with the increase of the sphere temperature the average velocity increases to a maximum value at a temperature of 400 °C and then decreases until the temperature reaches 700 °C, the average velocity will increase while the sphere temperature continually rises until the temperature reaches 900 °C. The average and the maximum velocity of the heated sphere are larger than those of the room-temperature sphere. The flow separates at the rear of the heated sphere, leading to low pressure drag. The drag reduction effect of the stable film boiling is lower than that of the nucleate boiling. In the nucleate boiling regime, the average velocity decreases with the increase of water temperature, the drag of the sphere with gentle boiling intensity is smaller. The vapor layer formed in the stable film boiling regime can improve the stability of the fall trajectory. The intense turbulence caused by the nucleate boiling can make the sphere largely deviate from rectilinear motion.
Drag reduction is an important problem in hydrodynamics for its close correlation with the applications in the fields of military, navigation, chemical engineering, etc.
There are many methods to reduce drag, such as by using polymeric additives,[1–3] microbubble injection,[4,5] exploiting supercavitation or partial cavitation,[6,7] and hydrophobic coating.[8–10] These methods reduce drag mainly by changing the surface characteristics of the object or by changing the viscosity of the fluid near the object.
Heating the object to a temperature above the boiling point, the surrounding liquid will vaporize. If the surface temperature is not high enough, bubbles will be formed around the object, and this boiling process is called nucleate boiling. If the temperature of the surface is significantly higher than the liquid’s boiling point, bubbles will immediately converge to form a vapor layer separating the object from the surrounding liquid, and this boiling process is called film boiling.
The vapor layer can be used to reduce the skin friction between an object surface and a fluid.[11–14] Saranadhi[13] heated a superhydrophobic surface of the inner rotor of a custom Taylor–Couette apparatus at a low superheat temperature to establish a stable and continuous vapor layer between the surface and the surrounding water. The vapor layer lubricates the interface, leading the friction drag to decrease. In their experiments, the skin friction can be reduced by 80% to 90% against unheated surface.
Recent studies have presented that the vapor layer formed in the film boiling regime can also be used to reduce the pressure drag caused by the difference between pressures in the front and the rear of the object.[15–20] Vakarelski et al.[17] investigated the drag reduction effects of the vapor layer when a free-falling sphere reached its terminal velocity in a fully fluorinated liquid with a low boiling point and a low latent heat of vaporization against water. They conducted the experiments in the subcritical range of Reynolds number, where the pressure-induced drag accounted for more than 95%. The hydrodynamic drag could be reduced by over 85% as shown by Vakarelski et al.[17] Therefore the vapor layer had to significantly change the pressure drag. For a sphere falling into a liquid, the farther the flow separation location away from the bottom of the sphere, the lower the pressure drag is. Vakarelski et al.[17,19,20] presented that the flow separation occurs at about the sphere’s equator for an unheated sphere, the lubrication of the vapor layer in the film boiling regime can make the separation point move to the rear of the sphere, resulting in the reduction of pressure drag.
Nucleate boiling was also formed in the Vakarelski et al.’s study.[17–19] The height of the water tank was between 1.6 m and 2 m. They calculated the drag coefficient by using the terminal velocity of the sphere when it was close to the bottom of the tank. For stable film boiling, a vapor layer still exists around the sphere during the falling process. The heat transfer intensity in the nucleate boiling regime is at least one order higher that in the stable film boiling regime. The intensity of nucleate boiling greatly decreases when the sphere reaches the bottom of the water tank. In Vakarelski et al.’s experiments,[17–19] nucleate boiling had only a small effect on the terminal velocity of the sphere. The drag reduction of nucleate boiling may be underestimated by using the Vakarelski et al.’s experimental method.[17–19]
In the present article, we show the average velocity of sphere in both nucleate boiling and film boiling regimes during the whole falling process into water with different temperatures. We investigate the sphere and water temperature effect on the drag reduction. Using a water tank with a height of 0.6 m, the duration of each experimental drop of the spheres is less than 0.7 s. The nucleate boiling can maintain a certain boiling intensity during the fall. For most trials, we find that the nucleate boiling has better drag reduction effect than the stable film boiling. We present the variation of falling velocity with time for a room-temperature sphere, a sphere in nucleate boiling regime and a sphere in stable film boiling regime and discuss the stabilities of the fall trajectory for the three cases.
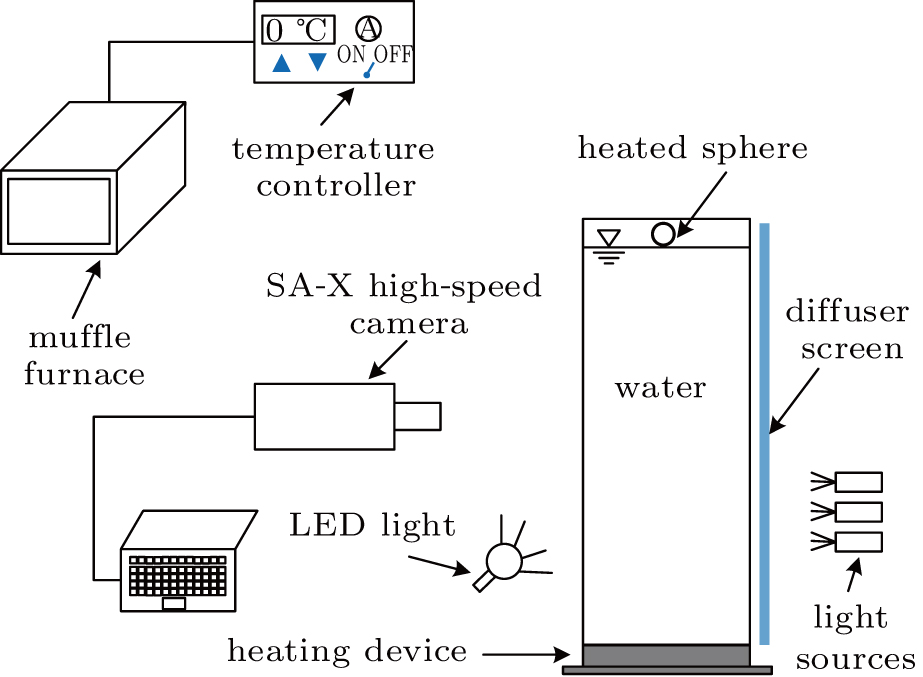
Our experimental setup is shown in Fig.
The sphere was heated in a muffle furnace and kept for more than an hour after the temperature displayed on the temperature controller had reached the preset value. The water was heated by using a heating device and stirred to obtain uniform temperature. When the water temperature reached the preset value, the sphere was taken out of the muffle furnace and released slightly above the water surface. In our experiments, the water temperatures were in a range of 25 °C–95 °C and the sphere temperatures were in a range of 25 °C–900 °C.
A high-speed camera (Photron Fastcam SA-X) was used to capture the falling processes of the spheres. The falling velocities were determined by the video clips. Uniform back lighting was achieved by a group of 6 × 500-W light sources illuminating a diffuser screen. A foreground light-emitting diode (LED) light was used to observe the flow conditions on the sphere surface.
We calculate the average velocity of a sphere from immerging into water to reaching the bottom of the water tank by using the video clips. Table
| Table 1. Average velocities for three cases with different water and sphere temperatures. . |
In Fig.
The surface state of a sphere has a great influence on the drag characteristics of the sphere moving into water. The surface flow states are different for different sphere temperatures as shown in Fig.
When the initial temperature of the sphere reaches 800 °C, vapor bubbles get together to form a vapor layer, which separates the sphere from the surrounding water. The thermal conductivity of vapor is much lower than that of water, so the boiling phenomenon becomes gentle as shown in Fig.
We suspect that the lubrication and the disturbance of the vapor are the two main reasons for reducing the drag. The lubrication can reduce the frictional drag. It can also reduce the pressure drag in some cases, such as the lubrication of the vapor layer as described by Vakarelski et al.[17] The disturbance of the vapor can increase the turbulence of the flow which can make the separation point move towards the rear of the sphere and reduce the drag. Different boiling states have different drag reduction effects. The gentle nucleate boiling can reduce more drag than the violent nucleate boiling as shown in Figs.
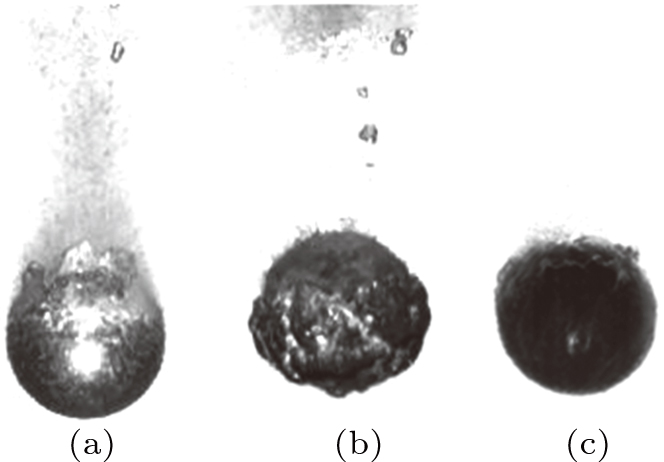 | Fig. 3. Surface states of the spheres at 20-cm underneath water surface at Ts = 400 °C (a), 600 °C (b), and 800 °C (c), with water temperature maintained at 25 °C in all cases. |
Figure
The drag coefficient of the sphere is CD = 2FD/(πR2ρV2). Here FD is the drag force and ρ is the fluid density. When the sphere reaches its terminal velocity, the drag coefficient can be defined as
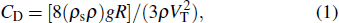 |
Figure
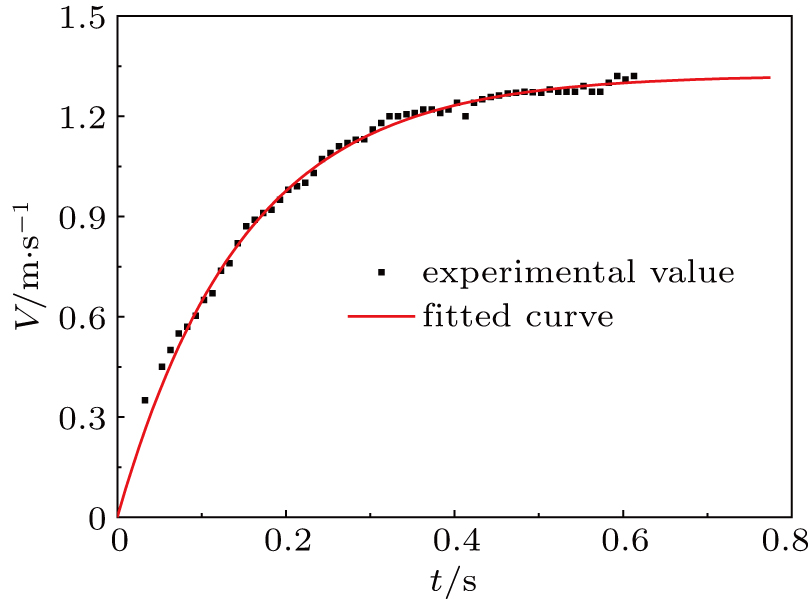
The maximum falling velocity shown in Fig.
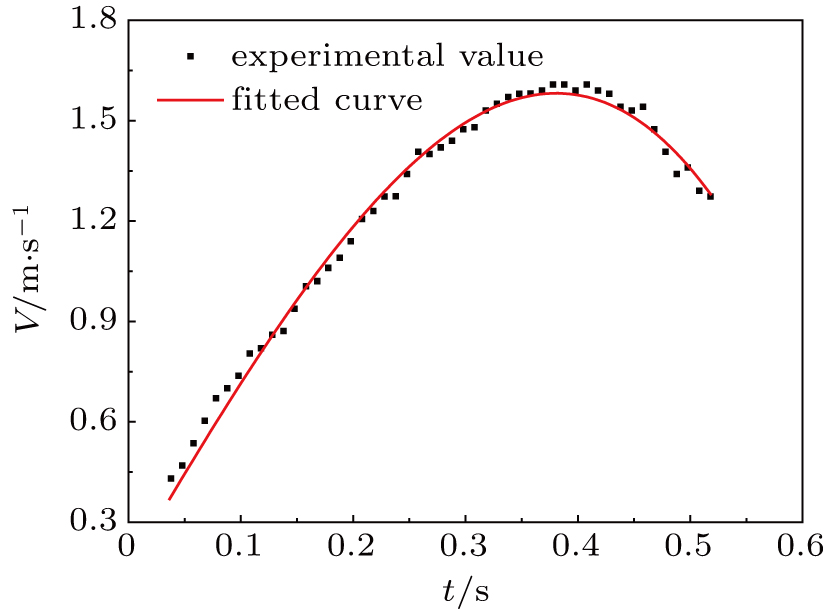
The falling velocity cannot keep its maximum value, and the drag reduction effect of the nucleate boiling weakens after t = 0.4 s, leading to the increase of fluid drag. The velocity and temperature of the sphere change with falling time, so do the nucleate boiling states. It is difficult for us to study the drag reduction characteristics of the sphere in nucleated boiling regime at different drop times. We can conclude that in this nucleate boiling case shown in Fig.
Figure
The data points inside the dashed ellipse represent the stable film boiling cases. When both of the water temperature and the sphere temperature are high, a stable and smooth vapor layer can be easily formed by converging the vaporized bubbles. The average velocities of the sphere with temperature Ts = 800 °C in an unstable film boiling regime for water temperature Tw = 25 °C and 50 °C, are close to each other. For Ts = 300 °C and 500 °C, the average falling velocity decreases with water temperature increasing. In the nucleate boiling state, the violent boiling and large bubbles have less drag reduction effect than the gentle boiling and small bubbles. The average falling velocity of the sphere in the stable film boiling regime is larger than that of the room-temperature sphere and smaller than that of the sphere in nucleate boiling and unstable film boiling regime as shown in Fig.
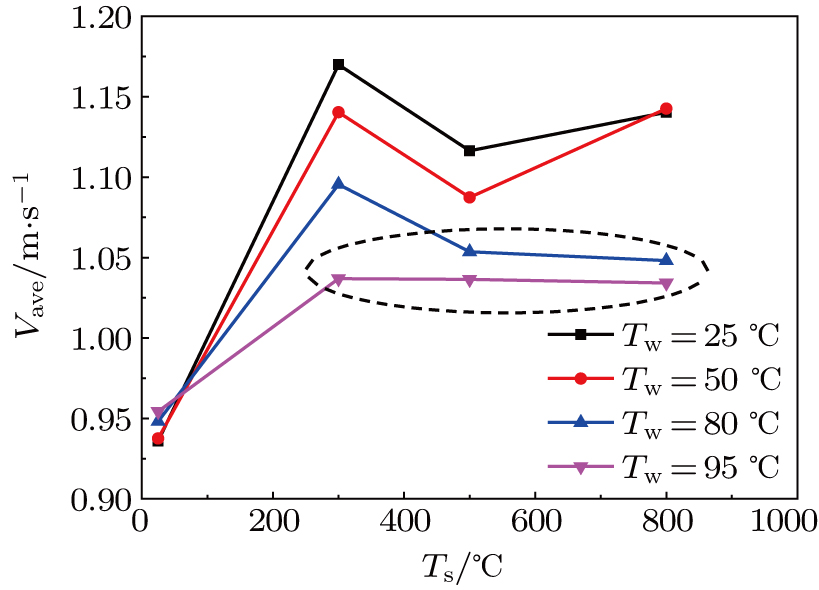 | Fig. 6. (color online) Plots of average velocity versus falling sphere temperature into different-temperature water. |
In Fig.
| Table 2. Maximum velocities and their corresponding drag coefficients for different values of Tw and Ts. . |
Vakarelski et al.[17–19] presented that the terminal velocities of the spheres in stable film boiling regime are much higher than those of the spheres in nucleate boiling regime. They also presented that the nucleate boiling just has a little effect on the terminal velocity. The test liquids were water with different temperatures and perfluorinated fluids with different viscosity. In their experiments, the height of the tank was in a range from 1.6 m to 2 m. The temperature of the sphere dropped quickly when falling in the liquid, and the intensity of the nucleate boiling was weak when the sphere reached the bottom of the tank. So it is hard to evaluate the drag reduction effect of the nucleate boiling in their experiments.
The height of the water tank in our experiment is 0.6 m. The nucleate boiling is more intensive when the sphere reaches the bottom of the tank than that in the experiments by Vakarelski et al.[17–19] As shown in Fig.
Figure
In Fig.
In Fig.
 | Fig. 8. (color online) Flow states around spheres at 40 cm underneath water surface at (a) Tw = 25 °C and Ts = 25 °C; (b) Tw = 95 °C and Ts = 500 °C; (c) Tw = 25 °C and Ts = 400 °C. |
In Fig.
As shown in Fig.
In Fig.
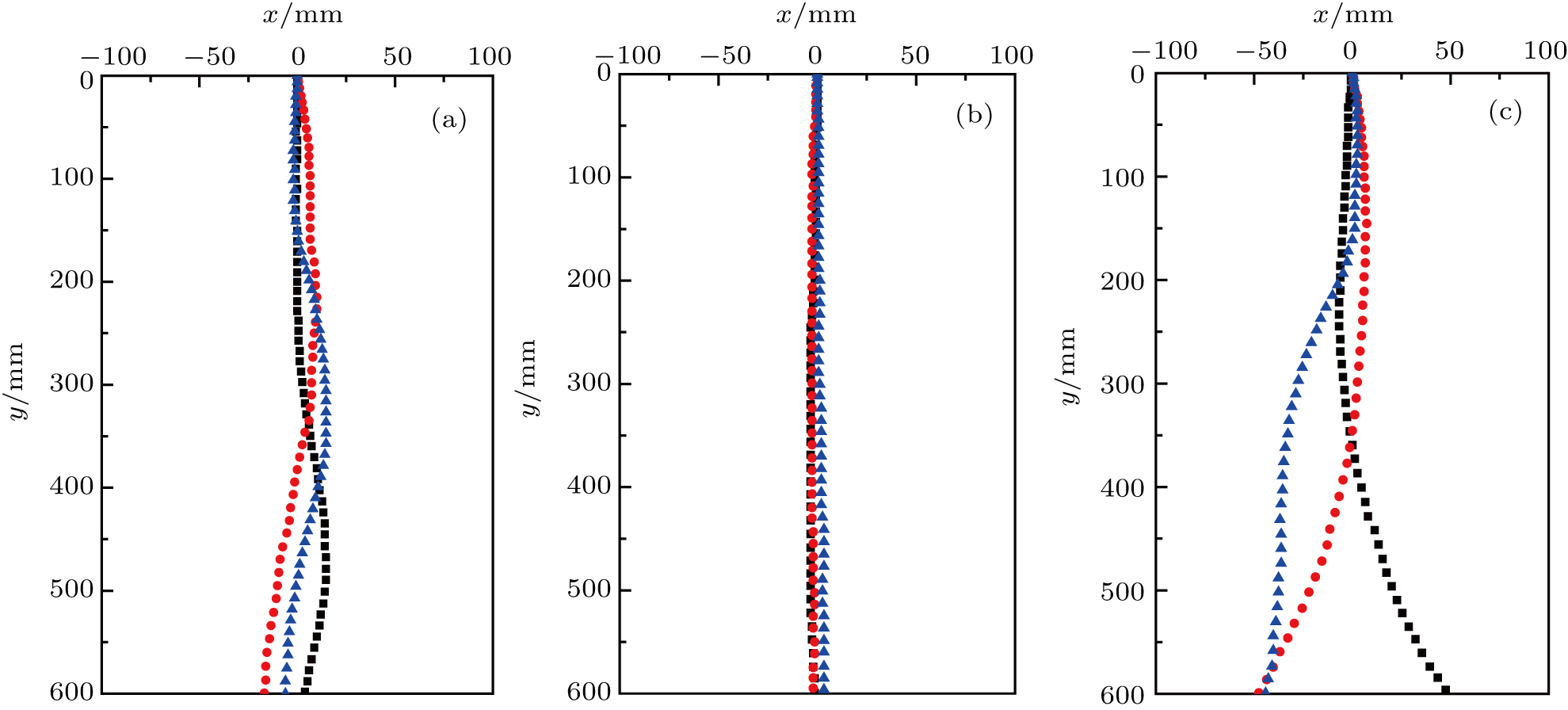
In accordance with Vakarelski et al.’s study[18] the trajectories of the falling spheres in stable film boiling regime (Fig.
In the present study, we also discuss the moving stability of the spheres in nucleate boiling regime. Like the behavior of a sphere in film boiling regime, for a sphere in nucleate boiling regime, the flow separation occurs in the rear of the sphere and the vortex area is narrower than that of a room-temperature sphere. The wake appears streamlined as shown in Fig.
We investigate the boiling effect on drag reduction during the falling process of a sphere in water. In 25 °C water, with the increase of the temperature of the sphere, the average falling velocity first increases and then decreases until the sphere temperature reaches 700 °C; the average velocity increases while the sphere temperature continues rising. In our experiments, the maximum average velocity appears at Ts = 400 °C and Tw = 25 °C and increases by about 28 percent compared with that for a room-temperature sphere. The drag reduction effect of the stable film boiling is lower than that of the nucleate boiling. In the nucleate boiling regime, the average velocity decreases with water temperature increasing, the drag of the sphere with gentle boiling intensity is smaller.
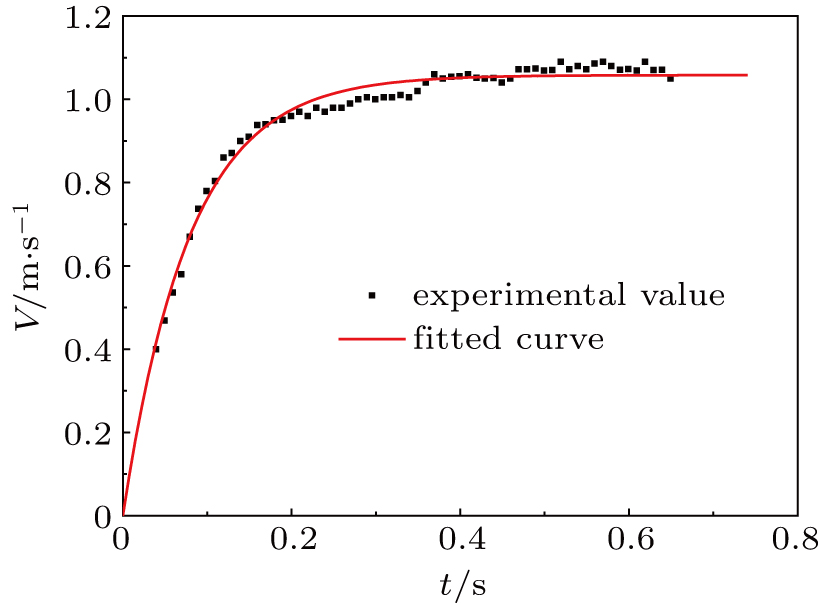
The exponential function: V(t) = VT (1e−t/τ) fits well to the experimental velocities for room-temperature spheres and spheres in stable film boiling regime. The velocity of the sphere in nucleate boiling regime at Ts = 400 °C and Tw = 25 °C increases to a maximum value at about t = 0.4 s. Then the velocity decreases until the sphere reaches the bottom of the water tank. The maximum velocity of the sphere in nucleate boiling regime is about 51 percent larger than that of the room-temperature sphere.
The flow separation position is a little lower than the equator of the room-temperature sphere. For heated spheres, the separation positions will move to the rear of the sphere. Comparing with the sphere in stable film boiling regime, for the sphere in nucleate boiling regime the discrete vapor bubbles are not easy to accumulate, thus leading to lower pressure drag. Compared with the room-temperature spheres, the spheres in stable film boiling regime have good moving stability and the spheres in nucleate boiling regime have large lateral displacements.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] |