† Corresponding author. E-mail:
Project supported by the National Natural Science Foundations of China (Grant No. 11305023). The author is deeply indebted to the Dalian University of Technology for providing the authority of utilizing the COMSOL software.
In this work, incompressible and compressible flows of background gas are characterized in argon inductively coupled plasma by using a fluid model, and the respective influence of the two flows on the plasma properties is specified. In the incompressible flow, only the velocity variable is calculated, while in the compressible flow, both the velocity and density variables are calculated. The compressible flow is more realistic; nevertheless, a comparison of the two types of flow is convenient for people to investigate the respective role of velocity and density variables. The peripheral symmetric profile of metastable density near the chamber sidewall is broken in the incompressible flow. At the compressible flow, the electron density increases and the electron temperature decreases. Meanwhile, the metastable density peak shifts to the dielectric window from the discharge center, besides for the peripheral density profile distortion, similar to the incompressible flow. The velocity profile at incompressible flow is not altered when changing the inlet velocity, whereas clear peak shift of velocity profile from the inlet to the outlet at compressible flow is observed as increasing the gas flow rate. The shift of velocity peak is more obvious at low pressures for it is easy to compress the rarefied gas. The velocity profile variations at compressible flow show people the concrete residing processes of background molecule and plasma species in the chamber at different flow rates. Of more significance is it implied that in the usual linear method that people use to calculate the residence time, one important parameter in the gas flow dynamics, needs to be rectified. The spatial profile of pressure simulated exhibits obvious spatial gradient. This is helpful for experimentalists to understand their gas pressure measurements that are always taken at the chamber outlet. At the end, the work specification and limitations are listed.
In low-pressure radio frequency plasma sources, the gas flow and heating, together with the neutral depletion, comprise the background gas dynamics. The gas dynamics are tightly coupled to the process of plasma production and transport, via their missions of providing feedstock species, exposing plasma to advection, re-distributing deposited energy, etc. Hence, investigations on the gas dynamics are useful for people to understand the plasma properties and processing techniques, in view of their attendance in delivering impinging ions and reactive radicals to the surfaces, where the material etching or film deposition is conducted. At present, most efforts on the gas heating scheme were aimed at measuring the gas temperature[1–3] and analyzing the heating mechanism,[4–6] e.g., elastic and charge exchange collisions and Franck–Condon. In addition, the influence of the gas heating on the magnitudes of electron density and temperature,[7] the varying trend of electron temperature against power,[8] the wave magnetic fields and skin effect,[9] etc., are also specified. As analyzed, the neutral depletion[10–13] is actually caused cooperatively by the pressure balance and gas heating. It could enhance plasma transport and result in non-monotonic variation of plasma density versus power.[14]
The gas flow[15,16] is caused by the system that feeds gas into the reactor and the pumping setup. A gas flow channel is formed between the locations of gas entrance nozzle and pumping port. The gas flow rate and the channel, together with the chamber dimension, cooperatively determine the residence time of feedstock gas in the reactor.[17,18] This parameter is important as it might be comparative to the timescale of plasma species crossing over the reactor via the diffusive and drift process and that of the chemical reactions with metastables. As a result, the plasma species densities changed with the residence time, as observed in Ref. [19]. In addition, the density profile alters when changing the gap between the electrodes due to the competition of the above time scales,[20] or by considering a gas flow module into the fluid model or not,[21] in a capacitively coupled plasma source. Still, the gas flow, together with the feedstock gas fragmentation, multi component mass transport, gas heating, pumping speed, etc., influence the accuracy of gas pressure measurements at the chamber outlet. Lastly, the pressure, spatially averaged, should increase with increasing the gas flow rate, which influence the plasma. In Ref. [22], the electron density and collisional power loss increased and the electron temperature decreased with the gas flow rate, in an inductively coupled Ar/Nxs2 plasma. All the above studies focus on the influence of gas flow on the plasma properties. Other gas flow works report on its inference on the aspects that relate to the plasma processing techniques, e.g., the ion flux profile,[23] the saturate current densities and its dependence on gas type (Ar versus C4F8),[24] the ion energy and angular distribution functions,[25] the Si etch rate with SF6 plasma,[26] the uniformity of deposition rate of hydrogenated silicon nitride film,[27] and the life cycle of silicon chloride etch product.[28]
The above literature review tells us that the gas flow plays very important role in both the plasma itself and the related processes. This is contradictory to the assertion that it had minor influence on the plasma due to the dominance of diffusion over advection in the bulk plasma, which was given early in Refs. [29] and [30]. We believe that the gas flow only exhibits its importance under certain conditions, which is cooperatively determined by the coupling mechanism of all the above factors mentioned, such as the residence time, chemical kinetics, pressure measurements, gas heating, feedstock molecules fragmentation, neutral depletion and pumping system, etc. Hence, it is of great importance to investigate the gas flow effect systematically. As reviewed, the gas flow effect in inductively coupled plasmas (ICPs) has been studied by several works. However, we feel that these studies are not enough, and not systematic either. For instance, the influence of gas flow on the density profiles of neutral species is yet reported. The magnitudes of diffusive and advective velocities of neutrals are in the same order, at strong flows. Hence, the advection ought to disturb the conventional density profiles of neutrals that are formed via pure diffusion, as expected. Besides, although the basic characteristics of flow velocity, i.e., streamline and magnitude, were given in Refs. [30] and [31], detailed structure, e.g., axial and radial velocity profiles, and their evolution as a function of flow rate and pressure, are not studied yet.
In this work, a two-dimensional fluid model is used to investigate the characteristics of background gas flow in an argon ICP, and meanwhile the advections of plasma species at incompressible and compressible gas flows are discussed. Logically, the compressible flow is more realistic. Nevertheless, we found that the utilization of incompressible flow and of its comparison to the compressible flow, can be very helpful for us to understand the respective behavior of velocity and density variables and their influence on the plasma. The pressures used in this work are selected in a range, i.e., 20 mTorr ∼ 50 mTorr (1 Torr = 1.33322 × 102 Pa), such that the gas flow kinetics studied are in the domain of fluid model. Meanwhile, at these pressures and the discharge frequency of 13.56 MHz, the experimentally measured electron energy distribution functions are found more or less Maxwellian,[32–35] which meets the requirement of electron fluid equations.
The two-dimensional axial symmetric ICP reactor used in this model is shown in Fig.
The gas phase and surface chemistries of argon plasma used in this model are listed in Tables
| Table 1. Gas phase electron impact collisions and chemical reactions.[36] . |
The space of the ICP chamber is discretized by the finite element method. The mesh set used in the simulations, i.e., mesh set I, is shown in Fig.
| Table 2. Surface reactions mechanism. . |
The inductively coupled plasma (ICP) and the single-phase flow (SPF) modules of the COMSOL software are taken for this gas flow study. The former module describes the plasma generation and transport, while the latter describes the background gas flow. The ICP module consists of electron, heavy species, electromagnetic field, and electrostatic field equations. In the SPF module, the Navier–Stocks equation is selected to study the incompressible gas flow, and the momentum conservation equation is selected for the compressible gas flow. The flow velocity and density of gas mixture, calculated from the SPF module, are sent to the ICP module in the compressible flow, while only the velocity variable is delivered in the incompressible flow. Reversely, the ICP module calculates the viscosity coefficient of gas mixture and transfer it to the two types of gas flow, besides for describing the plasma transport. The interacting mechanism of the two modules is shown in Fig.
 | Fig. 3. (color online) Interactions of single-phase flow (SPF) and inductively coupled plasma (ICP) modules in this study. |
The equations of electron density and energy are expressed as
 |
 |
 |
 |
Without the secondary electron emissions, the boundary conditions of the continuity and energy equations of electrons are defined as
 |
The heavy species means all plasma species except the electrons, i.e., grounded and excited argon atoms, and argon ions. In this heavy species module, an approximation is used. If there are totally Q heavy species, only the transports of Q − 1 species are described directly via the transport equation, i.e.,
 |
 |
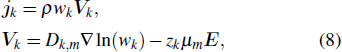 |
 |
 |
 |
The electromagnetic field in this discharge is calculated via the following equation,
 |
 |
The Poisson’s equation is used to calculate the electrostatic field,
 |
 |
When the temperature variation in the gas flow is insignificant and the flow velocity is low, i.e., with the Mach number less than 0.3, the flow can be assumed incompressible.[39] The Navier–Stocks equation can therefore be used, i.e.,
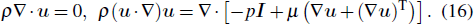 |
Slip velocity at the walls is negligible in this work due to the selected high-pressure range and no-slip boundary condition is therefore used. At the gas inlet, fixed inlet velocities are taken as boundary condition. At the chamber outlet, fixed gas pressure boundary condition is used. In the incompressible flow, the gas mixture density is fixed in the whole space, whose value is given via the state equation of ideal gas with the outlet pressure and the room gas temperature. Here, the validity of assuming room gas temperature will be discussed in the section of discussion and further remarks.
When the compressibility is taken into account, the continuity and momentum conservation equations are used for the gas flow, i.e.,
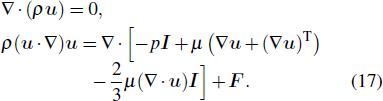 |
In Fig.
 | Fig. 4. (color online) Profiles of radial (a) and axial (b) velocity components for the inlet velocity of 200 m/s, the power of 200 W and the pressure of 20 mTorr, at the incompressible gas flow. |
In Fig.
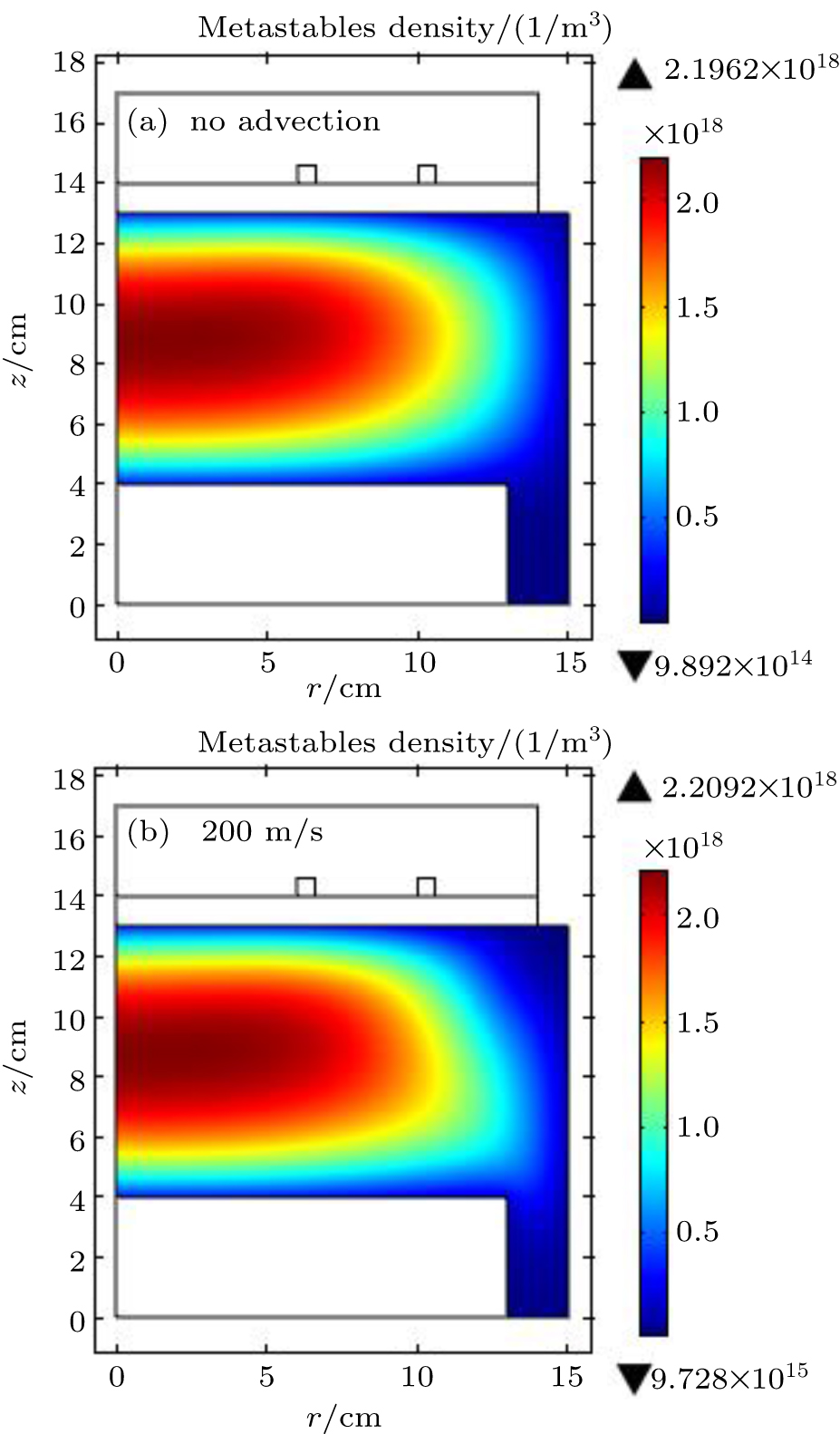 | Fig. 6. (color online) Metastables density profiles when the gas flow is not included (a) and at 200 m/s inlet velocity, at the discharge condition of 20 mTorr and 200 W. |
In Fig.
In Figs.
In Fig.
 | Fig. 10. (color online) Peaked values of electron density and temperature profiles versus the gas flow rate at 20 mTorr and 200 W. |
To explain the above discovering, in Fig.
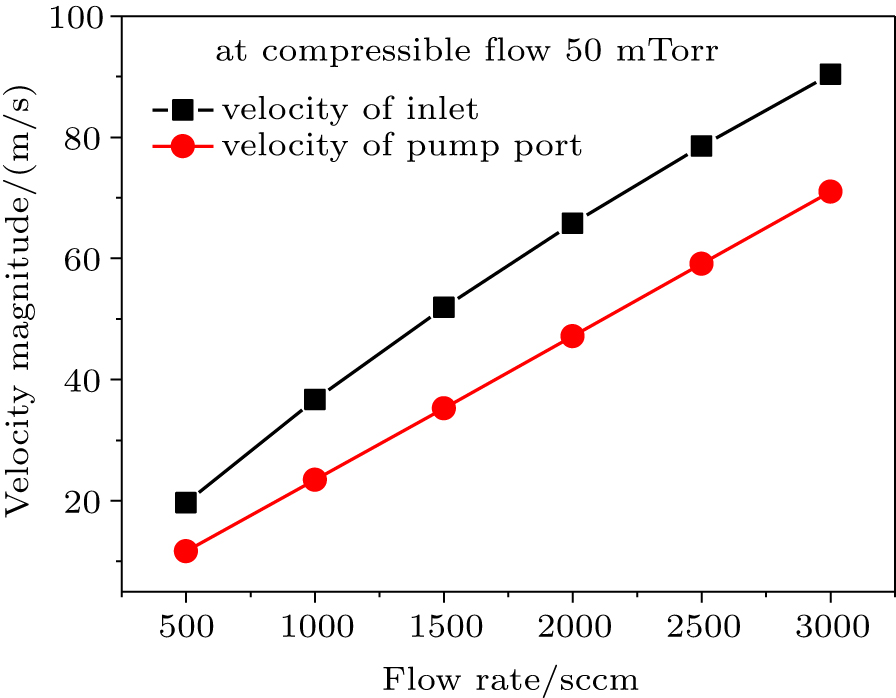
In Fig.
The velocity magnitude profiles at the inlet velocity of 100 m/s and at the inlet flow rates of 200 sccm and 2000 sccm are sequentially plotted in Fig.
The different characteristics of velocity magnitude profiles at the two flows are analyzed. At the incompressible flow with fixed mixture density, the gas flows freely across the chamber. Nevertheless, in the compressible flow the mixture density is varied, and the fluid becomes elastic. It can efficiently respond to the external disturbance via its pressure alteration, proportional to the mixture density alteration, as shown in Fig.
The influence of the compressibility on velocity magnitude profile becomes less important at high pressure, like 50 mTorr in Fig.
The flow velocity profile is tightly related with the residence time calculations and depicts the picture of plasma species residing in the chamber. Moreover, the velocity magnitude profile evolution implies that the residence time of background gas in the chamber might not be proportional to the gas flow rate, which is contradictory to the present recognition that based on one simple formula, τr = pV/(patmQ), where p is the gas pressure, V is the plasma volume, Q is the gas flow rate in units of standard cubic centimeter per minute (sccm), and Qatm is defined as atmosphere pressure.[42] The literature review revealed the importance of residence time in both the plasma dynamics and etching and deposition process.
In this work, the characteristics of both incompressible and compressible background gas flows and their influences on plasma in argon inductively coupled plasmas are investigated by a fluid model. The results show that incompressible flow can distort the conventional symmetric metastable density profile, and the compressible advection can bring to pressure effect, besides the neutral density profile distortions. The velocity profile of incompressible flow does not change as increasing the inlet velocity, while the velocity peak of compressible flow shifts from inlet to the pump port on increasing flow rate, due to the compressibility. The compressibility influence on velocity magnitude profile become less important at high pressure because of the difficulties in compressing dense gases. The compressible mixture density is considerably varied in gas flow channel, while more or less unchangeable in bulk chamber. This work helps people understand the relation of measured discharge pressure with the real bulk chamber pressure. Meanwhile, it reveals novel neutral density profiles via incompressible flow and depicts the resident process of plasma species via the flow velocity profile.
As described in the literature, the plasma transport can be substantially influenced by the neutral depletion process that is caused by gas heating effect and pressure balance.[10–14] This attendance of gas temperature in plasma dynamics is important only at rather high deposited power values, i.e., several kilowatts,[13,14] when the feedstock gas is severally depleted, plasma density is high enough, i.e., above 1018 cm−3, and the ionizing degree is high enough, i.e., larger than one percent. This is because that the gas heating effect is more obvious at high powers due to high plasma density and hence high collision rates that heats the gas.[8] Nevertheless, in this work, the power is fixed at 200 W, and the ionizing degree, 0.1%, is accordingly far lower than the above threshold, in a chamber with more or less the same size. Hence, it is believed that the findings of this model that aims at revealing gas flow characteristics ought to be insignificantly influenced if excluding the gas heating effect. In addition, the gas temperature increases with pressure due to high feedstock molecule density that increases the collision rates,[12] and hardly changed with flow rate, as observed in the experiment of Ref. [43]. These new features of gas heating effect, on the other hand, authenticate this discovery on the gas flow effect that is carried out at low pressure, 20 mTorr. As noted, the present study successfully decouples the gas flow and heating effects. This is useful for us to see each role of the effects in the discharge dynamics.
As we understood, the ion temperature is important in addressing the spatial transport of charged species via the diffusion and mobility of ions, and correlated to the gas heating effect via the elastic and charge exchange collisions between the charged and neutral species, which transfer energy from ions to neutrals. One paper has reported that the axial and radial profiles of plasma density, temperature and potential agreed well with the experiment, based on the ion mobility data predicted by the Monte Carlo technique and the local field approximation that calculates ion temperature, which is used to calculate the diffusion via the Einstein’s relation.[44] We believe that properly addressing ion temperature can be very helpful for the model to predict well the spatial characteristics of charged species. Clearly, this is out of the scope of the present work, which is focused on the gas flow effect. On the other hand, as found in our work, the ion density profile is not changed by the gas flow, due to the fact that the ion directional velocity is always several orders higher than the gas flow velocity. Therefore, we believe that the present work that attempts to reveal the qualitative trends of plasma against the gas flow, be insignificantly affected by utilizing room temperature assumption for the ions. Still, as the gas heating effect is less important at this low power selected in this work, the influence of ion temperature on the gas temperature[5] is therefore of no interest.
In the present work, the steady state gas flow equation is used. This indicates that plasma was produced and transported on one already established fields of flow velocity and mixture density. Hence, the influence of gas flow on the plasma is well explained. Nevertheless, the influence of plasma generation and transport on the gas flow is not properly addressed. Still, this is a two-dimensional simulation, hence the gas flow behavior across the radial and axial plane cannot be described yet. To sum up, in future works, it is expected that more insights about the gas dynamics can be revealed by considering the gas temperature and ion temperature kinetics, and meanwhile introducing the unsteady state and full dimensional gas flow equation.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] | |
| [39] | |
| [40] | |
| [41] | |
| [42] | |
| [43] | |
| [44] | |
| [45] | |
| [46] | |
| [47] | |
| [48] |