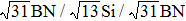† Corresponding author. E-mail:
Silicene is a promising 2D Dirac material as a building block for van der Waals heterostructures (vdWHs). Here we investigate the electronic properties of hexagonal boron nitride/silicene (BN/Si) vdWHs using first-principles calculations. We calculate the energy band structures of BN/Si/BN heterostructures with different rotation angles and find that the electronic properties of silicene are retained and protected robustly by the BN layers. In BN/Si/BN/Si/BN heterostructure, we find that the band structure near the Fermi energy is sensitive to the stacking configurations of the silicene layers due to interlayer coupling. The coupling is reduced by increasing the number of BN layers between the silicene layers and becomes negligible in BN/Si/(BN)3/Si/BN. In (BN)n/Si superlattices, the band structure undergoes a conversion from Dirac lines to Dirac points by increasing the number of BN layers between the silicene layers. Calculations of silicene sandwiched by other 2D materials reveal that silicene sandwiched by low-carbon-doped boron nitride or HfO2 is semiconducting.
Since the successful exfoliation of graphene in 2004,[1,2] more than a hundred intriguing 2D materials have been explored.[3–6] However, only a few of them are theoretically predicted to be Dirac materials.[7] The existence of Dirac cones in 2D materials gives rise to many novel physical properties, such as half-integer/fractional quantum Hall effect,[2,8–10] ultrahigh carrier mobility,[11] etc.[12] According to first-principles calculations,[13,14] monolayer silicene is a Dirac material with a stable buckled honeycomb structure.[15] The Fermi velocity of silicene is predicted to be ∼106 m/s, and its intrinsic carrier mobility has the same order of magnitude as that of graphene.[16] Besides, the electronic properties of silicene have a better tunability than those of graphene.[17–22] These novel properties together with the possibly inherent compatibility with traditional silicon-based nanotechnology make silicene a promising candidate for electronic devices and a distinct building block for van der Waals layered materials.
Silicene has been grown on several substrates, such as Ag(111),[23–26] Ir(111),[27,28] Ru(0001),[29] and ZrB2(0001).[30] Transistors have also been fabricated with epitaxial silicene on an Ag(111) thin film.[31] However, there is no convincing experimental evidence supporting the existence of Dirac cones in epitaxial silicene because of the strong coupling with these substrates.[27,29,30,32–37] Silicene’s surface is indeed very active because of the dangling Si bonds. The exposed silicene interacts easily with other active materials so that the electronic properties can be modified easily in unexpected ways. However, silicene has been found to interact weakly with graphene[38] and hexagonal boron nitride (BN).[17,39] Dirac cones of silicene shift above the Fermi level when sandwiched by graphene. In contrast, BN does not cause the shift of the Dirac cones. Therefore, BN-protected silicene could be a promising block for building van der Waals layered heterostructures (vdWHs). In addition, silicene sandwiched between some other 2D materials can be semiconducting, which is promising for applications in electronic devices.[40] Similar to the cases of molecules encapsulated by nanotubes or graphene layers, silicene is also energetically stabilized by the cladding layers.[41]
In this paper, we investigate electronic structures of BN-protected silicene in heterostructures and superlattices by first-principles calculations. Using “Si” to denote silicene, first we calculated the properties of BN/Si/BN heterostructures with different rotation angles and lateral shifts. The results show that rotation, lateral shift, and limited strain in silicene will not cause gap opening. To take advantage of the ultra-high carrier mobility of silicene, we propose a BN/Si/BN/Si/BN heterostructure, where each silicene layer is a conducting channel. We calculated its electronic properties. It is found that the band structure near the Fermi energy is sensitive to different stacking configurations of silicene layers due to interlayer coupling between the silicene layers. The coupling becomes negligible when the silicene layers are separated by three BN layers in the BN/Si/(BN)n/Si/BN heterostructure. We also calculated potential (BN)n/Si superlattices, and found that a conversion between Dirac points to Dirac lines can be achieved by changing the number of BN layers between the silicene layers. Moreover, we calculated the band structures of silicene sandwiched by low-carbon-doped BN (l-BCN), high-carbon-doped BN (h-BCN), and HfO2 and graphene/Si/BN. We found that the Dirac cones of silicene are opened in all of these heterostructures, but only l-BCN/Si/l-BCN and HfO2/Si/HfO2 are semiconducting with band gaps of 19 meV and 131 meV, respectively.
All quantum-mechanical calculations were carried out based on the density functional theory (DFT) as implemented in the Vienna ab-initio simulation package (VASP).[42–44] Electron–ion interactions were represented by projected augmented wave (PAW) potentials.[45] Exchange–correlation interactions were treated within the generalized gradient approximation (GGA-PBE).[46] The method of DFT-D3 to include van der Waals interactions was used in all the calculations of heterostructures.[47] The wave functions were expanded using a plane-wave basis set with an energy cutoff of 520 eV. For 2D structures, a vacuum layer larger than 20 Å was used to avoid interactions between layers in neighboring supercells. The force on each atom was relaxed to less than 0.01 eV/Å. The Brillouin zone was sampled using a Γ-centered 18 × 18 mesh for (2 × 2) silicene in self-consistent calculations.
It has been reported that the Dirac cone of silicene is protected when a (2 × 2) silicene is sandwiched by two (3 × 3) BN layers.[17] While in the real fabricating process, there are always lattice mismatches, rotation angles (misalignment), strains, and so on. To investigate the effects of the above-mentioned situations in heterostructures, we build different BN/Si/BN supercells with different stacking configurations and calculate the energy band structures. The results are presented in Table
| Table 1. Silicene sandwiched by BN with different rotation angles and lattice mismatches. . |
To eliminate the effect of strain in silicene in these heterostructures, the lattice constant of silicene is kept the same as that of its free-standing state and the heterostructures are otherwise fully relaxed. For all the BN/Si/BN heterostructures shown in Table
As a result of the small binding energy, there are probably different rotation angles in BN/Si heterostructures in the fabrication process. The calculations show that the electronic properties are nearly not affected by the rotation angles for the BN/Si heterostructures due to weak van der Waals interaction. We also investigate the impact of lateral shifts in BN/Si/BN. Our calculations show that lateral shifts almost have no effect on both the electronic properties and the total energy. Considering the possible strain in the silicene layer induced by lattice mismatches in heterostructures, we calculate the energy band structure of silicene under strain (less than 3%). The calculation results show that the Dirac cones are not opened up and the electronic properties are nearly not affected by the strain. Moreover, the possible lattice distortion or rumpling induced by the local strain would only have an effect on the local electronic properties. Therefore, we conclude that the electronic properties of silicene are protected robustly when sandwiched between BN layers.
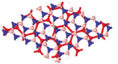
Since silicene is left intact when sandwiched between BN layers under different rotation angles, lateral shifts, and limited strains in silicene, we use BN/Si/BN as a building block for multilayer heterostructures. To take advantage of the ultra-high carrier mobility of silicene, we propose a multilayer BN/Si heterostructure, where each silicene layer is a conducting channel. We first discuss potential BN/Si/BN/Si/BN heterostructures, in which two silicene layers are positioned in an A-A stacking configuration. The structures and calculation results of BN/Si/BN/Si/BN are shown in Fig.
The distance between the two silicene layers in BN/Si/BN/Si/BN is 7.6 Å. When two silicene layers are separated by a vacuum layer of 7.6 Å, there is nearly no interaction between them and their Dirac cones are overlapped. On the other hand, the energy states of BN/Si/BN/Si/BN near the Fermi level (EF ± 0.3 eV) are contributed by both silicene and BN layers, as seen from the partial charge density in Fig.
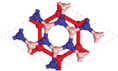
To further investigate the interlayer coupling and its impact on the electronic properties, we increase the number of BN layers between silicene layers. The energy band structures of the BN/Si/(BN)n/Si/BN and BN/Si/(BN)n/Si/BN structures are shown in Figs.
In the heterostructures mentioned above, only A-A stacking silicene layers are considered. Because of the weak binding between BN and silicene in BN/Si heterostructures, there can be different sequences for silicene layers during fabrication in experiments. We investigate the impact of different stacking configurations of these two silicene layers resembling bilayer graphene. For graphene, there are two common stacking configurations, A-A stacking and A-B stacking. Different from graphene, there are five different high-symmetry stacking configurations for two silicene layers due to its buckled structure. The heterostructures and the energy band structures near the Fermi level are shown in Fig.
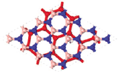
We further investigate (BN)n/silicene superlattices, in which the silicene layers are positioned in A-A configuration, with n = 1, 2, 3. The unit cell and the first Brillouin zone are shown in Fig.
It is important to open a gap in silicene for its application in electronic devices. Many different ways have been proposed to achieve this goal based on theoretical calculations.[17–22] Here we present the results that silicene sandwiched by l-BCN or HfO2 is semiconducting. We calculate the band structures of Gr/Si/BN, BCN/Si/BCN, and HfO2/Si/HfO2 heterostructures. BCN can be fabricated from either BN[49] or graphene[50] and has a tunable gap depending on the doping concentration. The atomic models of l-BCN and h-BCN used in our calculations are presented in Fig.
Dirac cones of silicene in Gr/Si/BN are slightly opened because of the breaking of the space-inversion, as shown in Fig.
HfO2 is a large-gap semiconductor, like BN. However, in HfO2/Si/HfO2 (Fig.
In BN/Si/BN heterostructures with different rotation angles, lateral shifts, and limited strains, the electronic property of silicene is protected robustly. In BN/Si/BN/Si/BN heterostructure, the band structure is sensitive to the stacking configurations of the silicene layers due to interlayer coupling. The coupling can be inhibited by increasing the number of BN layers and becomes negligible at three BN layers. In BN/Si superlattices with silicene positioned in A-A stacking configuration, a conversion between Dirac lines and Dirac points can be achieved by changing the number of BN layers between the silicene layers. Quasi-free-standing silicene can only be achieved in the BN/Si superlattice when adjacent silicene layers are separated by at least three BN layers. Multi-conducting-channel BN/Si heterostructures are only possible when the silicene layers are separated by no less than three BN layers. Besides, it is safer to use at least three BN layers on each side of silicene to protect the Dirac cones. At last, silicene sandwiched by l-BCN or HfO2 is semiconducting.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] | |
| [39] | |
| [40] | |
| [41] | |
| [42] | |
| [43] | |
| [44] | |
| [45] | |
| [46] | |
| [47] | |
| [48] | |
| [49] | |
| [50] |