Project supported by the National Natural Science Foundation of China (Grant Nos. 51605079 and 51475076), the Science Fund for Creative Research Groups of the National Natural Science Foundation of China (Grant No. 51621064), and the China Postdoctoral Science Foundation (Grant No. 2016M591424).
Project supported by the National Natural Science Foundation of China (Grant Nos. 51605079 and 51475076), the Science Fund for Creative Research Groups of the National Natural Science Foundation of China (Grant No. 51621064), and the China Postdoctoral Science Foundation (Grant No. 2016M591424).
† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant Nos. 51605079 and 51475076), the Science Fund for Creative Research Groups of the National Natural Science Foundation of China (Grant No. 51621064), and the China Postdoctoral Science Foundation (Grant No. 2016M591424).
The polymer spin coating is critical in flexible electronic manufaction and micro-electro-mechanical system (MEMS) devices due to its simple operation, and uniformly coated layers. Some researchers focus on the effects of spin coating parameters such as wafer rotating speed, the viscosity of the coating liquid and solvent evaporation on final film thickness. In this work, the influence of substrate curvature on film thickness distribution is considered. A new parameter which represents the edge bead effect ratio (re) is proposed to investigate the influence factor of edge bead effect. Several operation parameters including the curvature of the substrate and the wafer-spin speed are taken into account to study the effects on the film thickness uniformity and edge-bead ratio. The morphologies and film thickness values of the spin-coated PDMS films under various substrate curvatures and coating speeds are measured with laser confocal microscopy. According to the results, both the convex and concave substrate will help to reduce the edge-bead effect significantly and thin film with better surface morphology can be obtained at high spin speed. Additionally, the relationship between the edge-bead ratio and the thin film thickness is like parabolic curve instead of linear dependence. This work may contribute to the mass production of flexible electronic devices.
Spin coating is currently the predominant technique to produce uniform thin films with the thickness values on the order of micrometers and nanometers in the electronics and other industries.[1–6] For micro-electro-mechanical system (MEMS) devices, part of photoresist films are used as final structures of devices. Therefore, the thickness of the film determines the design of device and its uniformity is highly required. It is difficult to apply a highly uniform film to a planar substrate over a large area (ϕ > 30 cm) with a highly controllable and reproducible film thickness due to the fluid dynamic behaviors.[7,8] In many cases, the coating material is polymeric and is used in the form of a solution from which the solvent evaporates. Centrifugal force is one of the driving forces to make the solution move outward along the radial direction. The viscous force and surface tension cause a thin residual film to be retained on the flat substrate. Several processing parameters involved in the spinning process are dispensing volume, final spin speed, substrate flatness, solution viscosity, solution concentration, spin time, etc.[9–11] The importance of spin coating is manifested in its widespread application in science and industry. It is thus desirable to gain a detailed understanding of the spin coating process from both an experimental and a theoretical point of view.[12]
The pioneering analysis of spin coating was performed more than fifty years ago by Emile et al.[13] who considered the spreading of a thin axisymmetric film of Newtonian fluid on a planner substrate rotating with constant angular velocity. According to the Emslie’s model, Washo et al.[14] considered the effects of different droplet dispense methods on the thickness of the film based on the Navier–Stokes equation to obtain the corresponding model and formula in 1977. They assumed that the spin coating method was a disk rotation system, and the solution used was Newtonian fluid. The effects of Coriolis force, fluid gravity, solvent evaporation, substrate wettability, and the interface properties of air and solution have not been taken into account. However, this model directly reveals the essential dynamics of the spin coating process for future studies. After that, Bornside and Lawrence investigated the viscosity of the polymer solution and the effect of the spin angle on film thickness based on the ideal mechanic model established by Emslie. They revealed that the overall concentration of the polymer solution is constant and only the concentration near the free surface boundary layer is varied.[15,16] However, Bornside and Lawrence did not consider the influences of gradual curing of free surface on solvent evaporation rate and solution concentration. Mouhamad Y et al.[17] studied the dynamics of polymer film formation in the spin coating process. A semi-empirical model was proposed to permit the calculation of the solvent evaporation rate and the temporal evolution of the solute volume fraction and solution viscosity. Solvent evaporation is one of the main determinants of film curing, which has a significant effect on the film thickness. Moreover, the change of solution concentration directly affects the rheological properties of the solution. Also, it will affect the uniformity of film thickness distribution.
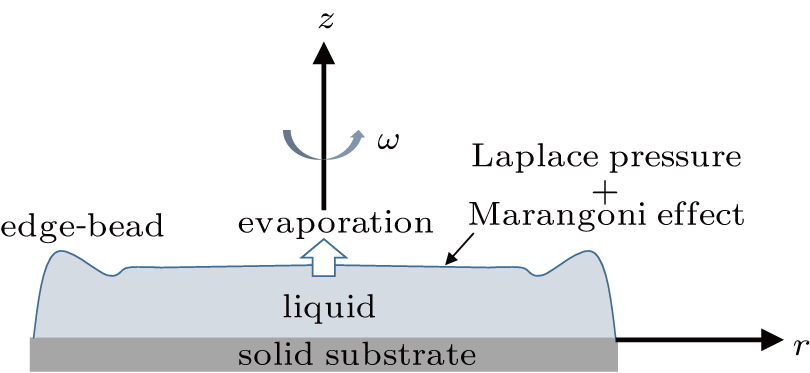
The edge-bead effect is one of the most critical problems, which affects the film thickness distribution. Mack C et al.[18] investigated the edge-bead formation mechanism which has been understood in terms of a surface tension of the resist fluid. At the edge of the coated liquid film, the surface should have a curvature larger than that in the flat central region. It reveals that the Laplace pressure due to the surface tension acting as smoothening the curvature distribution around the edge region. Na J Y et al.[19] characterized the effect of the spin-coating time on the microstructure evolution during semiconducting polymer solidification to establish the relationship between this parameter and the performances of the resulting polymer field-effect transistors (FETs). According to the results, a short spin-coating time of a few seconds, dramatically improved the morphology and molecular order in a conjugated polymer thin film. Shiratori S[20] establishes a new model to predict the dominant physics for the double-peaked edge-bead formation process. It has been concluded that the capillary flow which was caused by the evaporation of the solvent, was the dominant physics for the double-peak formation.
Even though spin coating has been universally used in the industry for a long time, more theoretical and experimental study are still in great demand to improve the machining technology.[21–24] The influence of the curvature of the substrate on the uniformity of film thickness distribution has not been studied in depth. If the interaction between the polymer and the substrate is strong, it will affect the dynamic behaviors of the polymer segments on the surface of the substrate. And this can also induce the non-uniformity of film thickness distribution. The present work is to clarify the effects of spin coating substrate and spin speed on film thickness distribution. Also, the dominant physics of edge-bead phenomena is investigated. An accurate analysis of spin coating will permit better design and control of the process in its various applications.
The polymer film was formed by spin coating of PDMS (Sylgard184 Silicone Elastomer, Dow Corning, Midland, MI) solution which is formed by mixing the prepolymer and curing agent of PDMS in a 10 : 1 ratio by mass with a spin coater (KW-4A, SETCAS Electronics Co., Ltd) as shown in Fig.
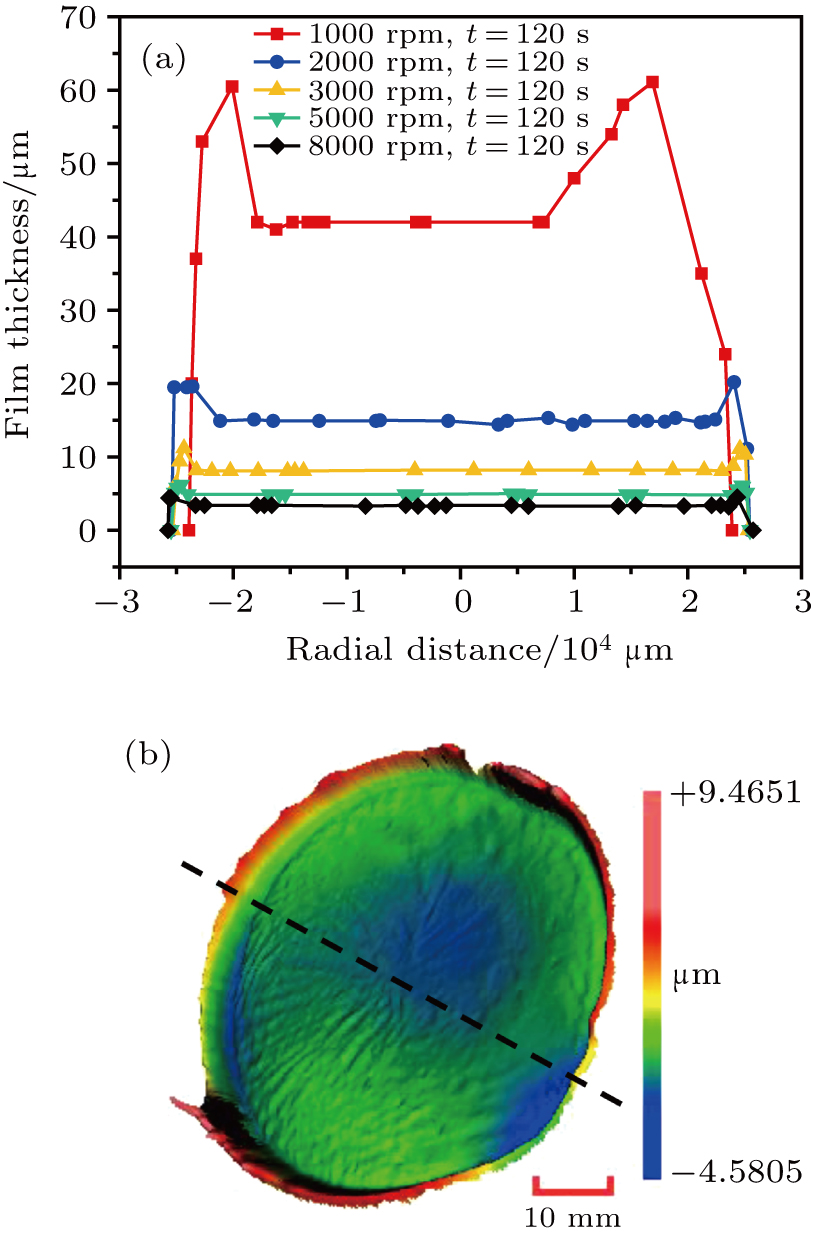
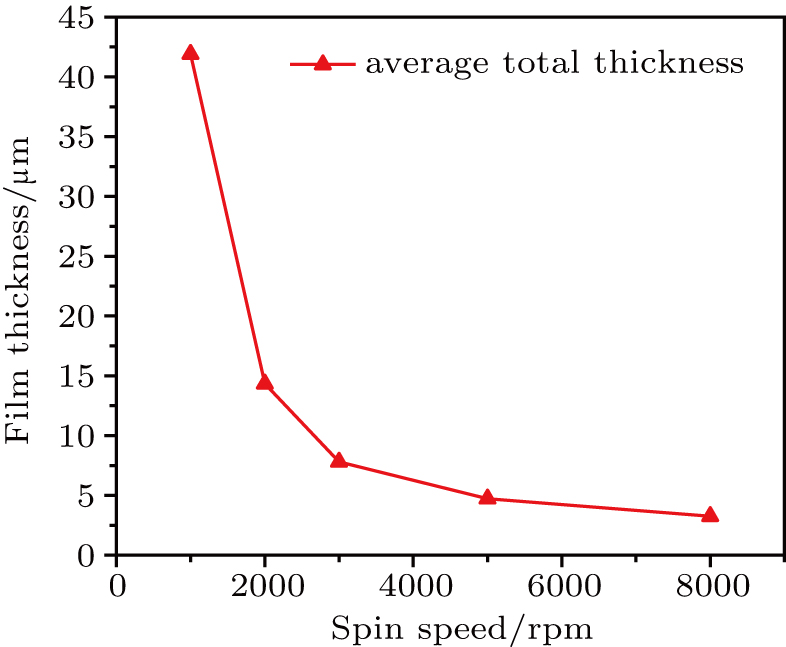
In this part, the polished silicon wafer is used as the planar substrate with the PV (Peak–Valley) value smaller than 5 μm. Five groups of experiments with various speeds (1000 rpm, 2000 rpm, 3000 rpm, 5000 rpm, 8000 rpm) are done to study the influence of spin speed on film thickness distribution. The film thickness distribution is measured along the radial direction as displayed in Fig.
It could be concluded that the film thickness is nonlinearly related to spin speed. The largest total average film thickness is 41.9 μm at a spin speed of 1000 rpm with large edge-bead effect area, and the edge-bead thickness is about 60 μm. In this work, the edge-bead effect area refers to the area near the wafer edge and the film thickness increases sharply in this region. The smallest total average film thickness is 3.25 μm with a smaller edge-bead effect area with a thickness of 4.4 μm at a spin speed of 8000 rpm. The edge-bead effect is mainly due to the fact that the fluid properties dictate a constant angle at the solid/liquid/gas interface and a thick edge-bead is confined at the wafer edge. And the Laplace pressure will move fluids from the side to the upper region. Another reason for such a film pattern is the increasing of friction with air at the periphery, resulting in forming a dry skin at the edge and impeding fluid flow.[20] As a result, the fluid in the center of the substrate, which is still kept being driven out by centrifugal force, begins to flow over the dry film and dries, resulting in buildup at the edge-bead. The spreading of a thin, viscous, film of liquid under the external centrifugal force is comprised of two regions. The first region is a flat region and the dynamics of which is determined by the balance between driving forces and viscous dissipation. The second region is near the advancing front, the curvature of which is governed by the interplay between the liquid surface tension and the driving force. When the spinning is stopped, the force balance suddenly changes due to a loss of the centrifugal force. At this stage, the liquid motion is dominated by the Laplace pressure, and it quickly moves fluids from the side to the upper region. In this way, the single edge-bead is formed shortly after the spin-stopping.[25–27]
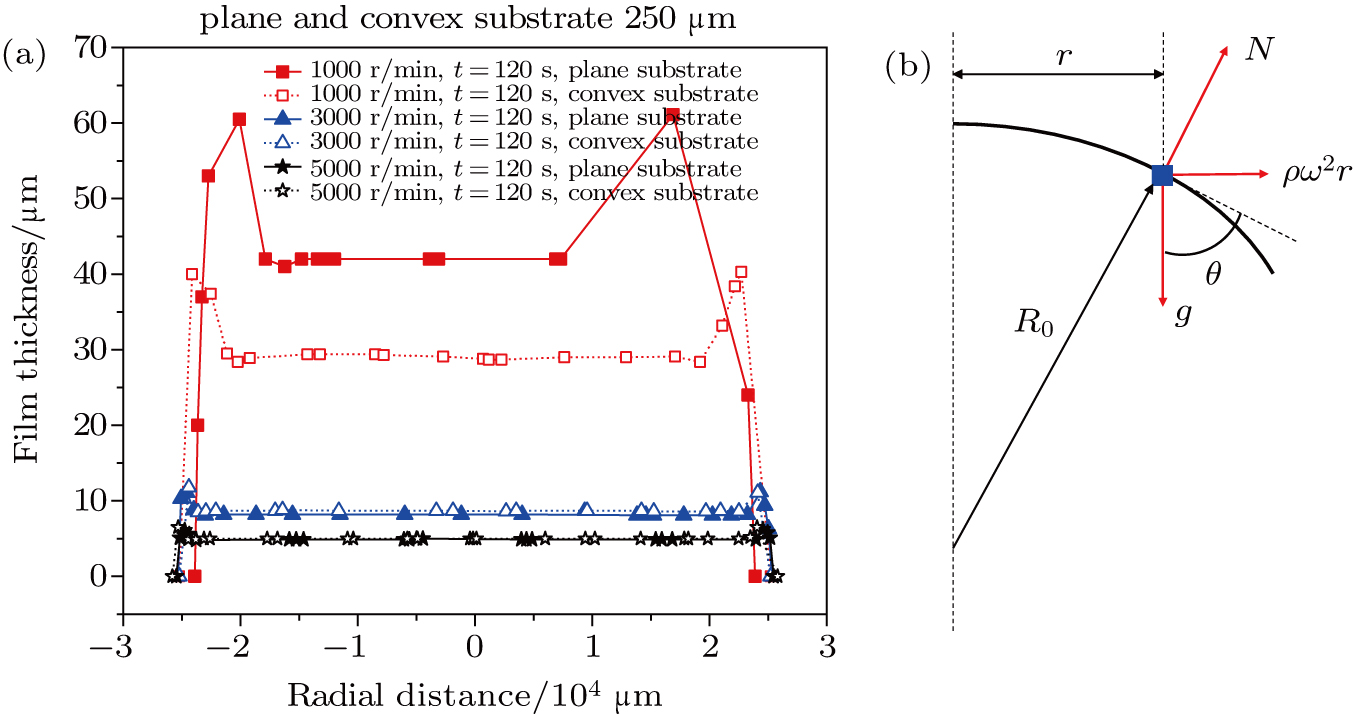
In this part, spin coating on the different slightly deformed substrates is investigated in detail. As shown in Fig.
To make the concave substrate, a circular sheet and a ring of stainless steel are used. As presented in Fig.
As displayed in Fig.
| Table 1.
Characteristics of film thickness and edge-bead effect ratio for the planar, convex, and concave substrate at different spin speeds. . |
The mechanical schematic plot of the PDMS micro-unit on the convex substrate during spin coating is presented in Fig.
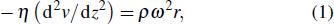 |
However, for the convex substrate, the balance is given by
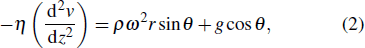 |
 |
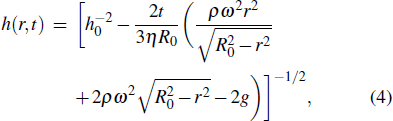 |
At a slow spin speed of 1000 rpm, the centrifugal force is not strong enough to overcome the liquid surface energy and thus the curvature of the solution is like a flat droplet. According to Eq. (
Convex substrates with different center deformations are also discussed in this experiment. Based on the results in Fig.
Figure
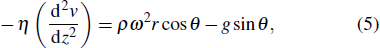 |
However, for the convex substrate, the balance is described by
 |
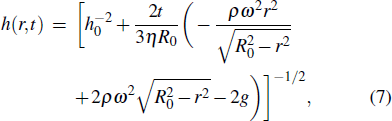 |
According to the results, it is much easier to obtain the polymer film of more uniform thickness with a convex or concave substrate. The concave substrate will force the liquid flow towards the center region based on Eqs. (
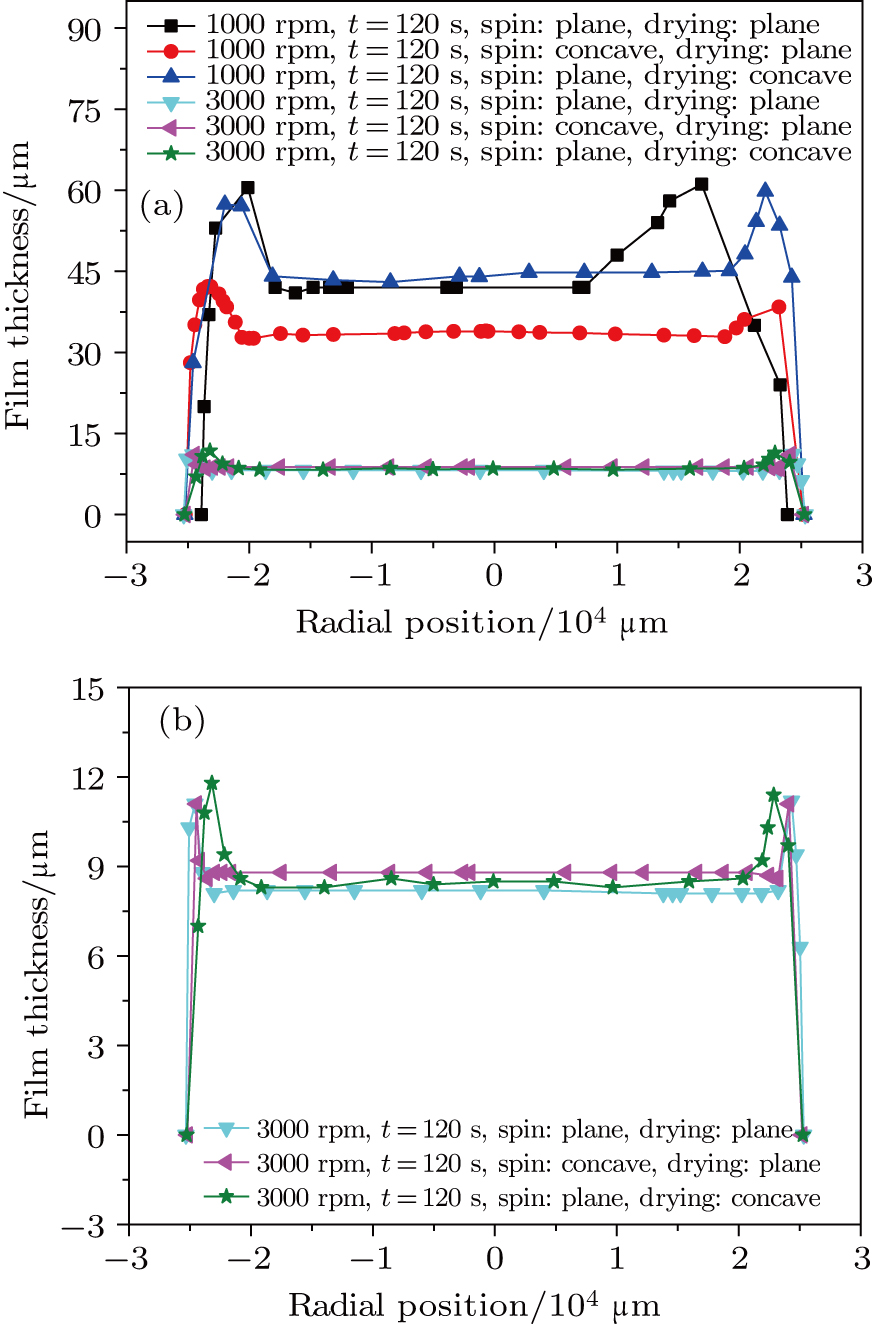
In order to study the dynamic behaviors of PDMS solution after spin-coated on a silicon wafer, the wafer with a concave deformation in the center region is dried in the oven. To make the concave substrate, a device is designed as displayed in Fig.
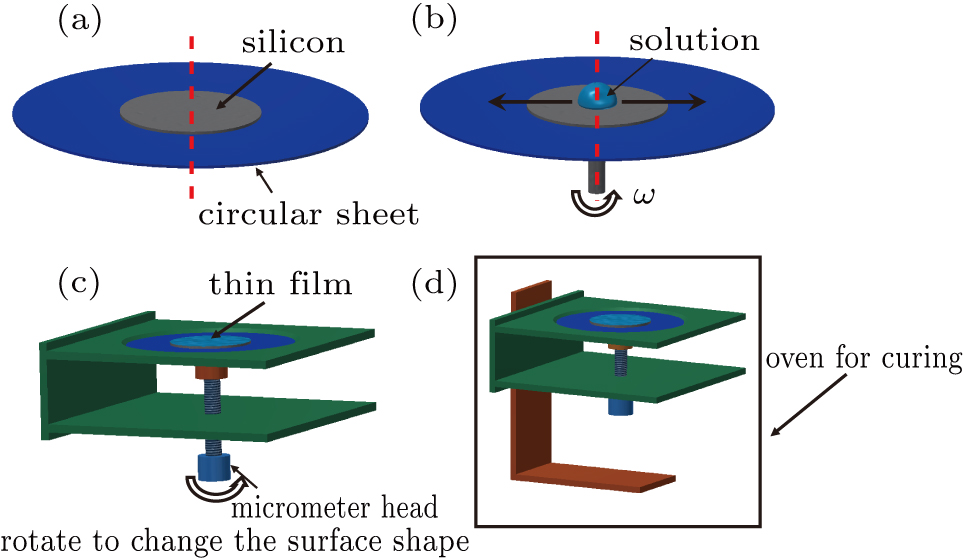 | Fig. 8. (color online) Schematic diagrams for the process of spin coating on a planar substrate and curing on the concave substrate. |
The film thickness distributions along the radial direction of the planar substrate and the concave substrate (center deformation 450 μm) at the spin speed of 1000 rpm and 3000 rpm are displayed in Fig.
The polymer film suffers several physical changes such as a spreading process and a drying process, which results in a non-uniform distribution of the thickness. One of the most known thickness undulations is the “edge-bead effect” which appears as a thick ridge along a periphery of the substrate. The edge-bead causes serious problems such as a particulate contamination due to a crack of the bead by mechanical wafer handlers. The bead also stands as an obstacle for a proximity exposure. The mechanism of the edge-bead formation can be understood in terms of a surface tension of the resist fluid. At the beginning of the spin coating process, a specified volume of the liquid is dispersed in the center of the substrate. Then, it is spread by the centrifugal force, and the liquid flows radially outward across the substrate. When the spinning is stopped, the force balance suddenly changes due to a loss of the centrifugal force. At this stage, the liquid motion is dominated by the Laplace pressure. Since the curvature of the substrate has a steep gradient at the junction between the upper and the side regions of the substrate, Laplace pressure can reduce the curvature distribution, and it quickly moves fluids from the side to the upper region (Fig.
The characteristics of film thickness and edge-bead effect ratio for the planar, convex and concave substrate at different spin speeds are displayed in Table
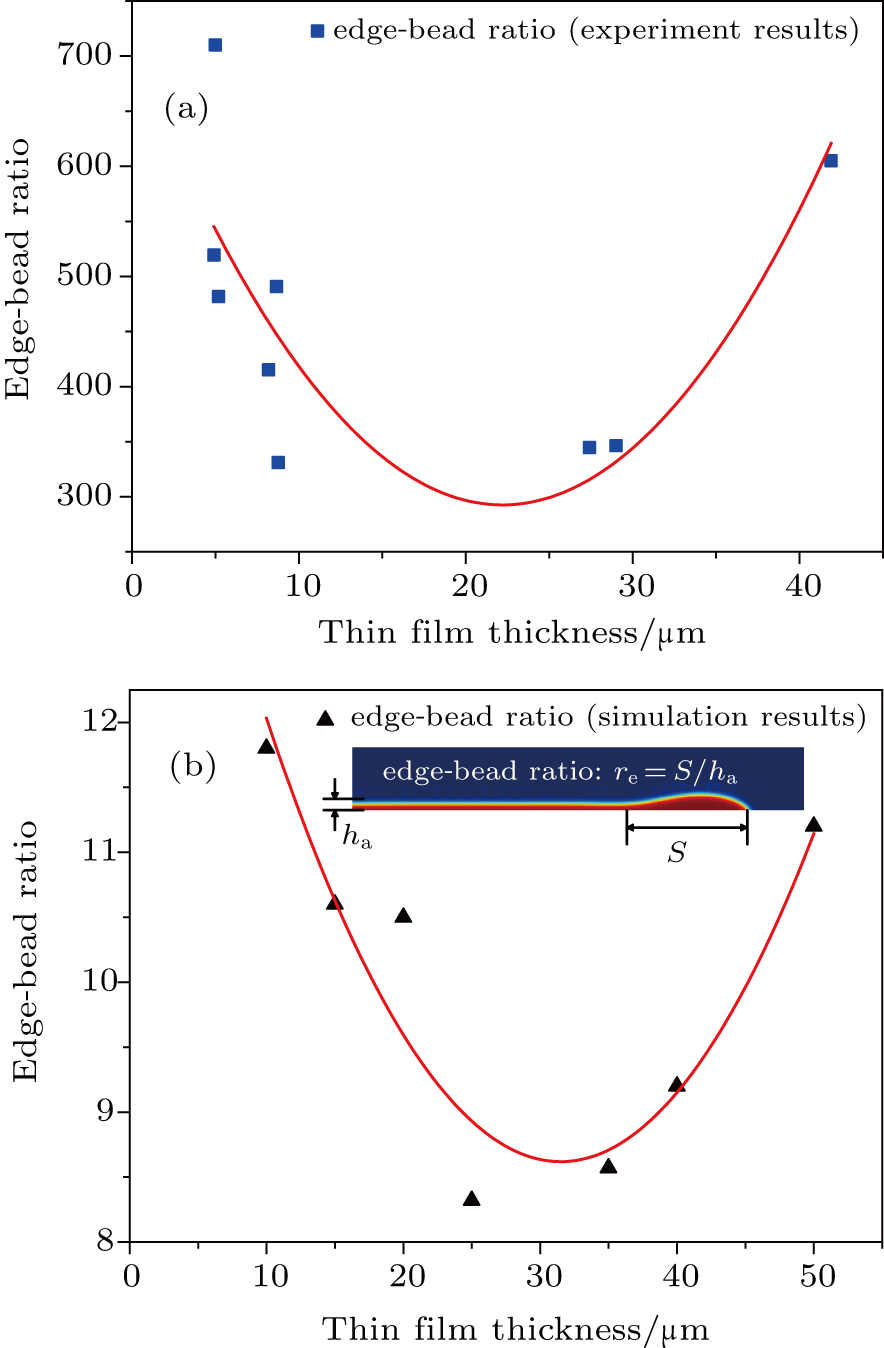 | Fig. 11. (color online) (a) Experimental and (b) simulation results of edge-bead effect ratio versus thin film thickness. |
A scaled-down model is set up to avoid the large calculation cost. The calculation is based on finite element method (FEM) and the weighted residual approach in the weak solution form is obtained. The minimum element size is 0.002 mm and the maximum element size is 0.045 mm. The simulation results are shown in Fig.
In this paper, to clarify the influences of substrate and spin speed on thin film thickness distribution in the spin coating process, both the experimental and theoretical investigations are presented. With the help of the laser confocal microscope, the film thickness can be described more accurately. It can be concluded that at high spin speed (> 1000 rpm), the film thickness is mainly manipulated by the centrifugal force instead of other parameters such as curvature of the substrate. However, at low spin speed, the film thickness distribution largely depends on the curvature of the substrate. Additionally, an interesting phenomenon about the edge-bead effect of the spin-coated film is observed. It is the convex and concave substrate that will lead to smaller edge-bead effect than that of a planar substrate. Also, the edge-bead ratio is mainly influenced by the film thickness and its relation to thickness is in the form of a parabola-like curve. It seems that the edge-bead effect is mainly induced by the Laplace pressure and solution viscosity. It is worth further studying.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] |