† Corresponding author. E-mail:
A systematic interpretation of laser-induced damage in the nanosecond regime is realized with a defect distribution buried inside the redeposited layer arising from a polishing process. Under the 355-nm laser irradiation, the size dependence of the defect embedded in the fused silica can be illustrated through the thermal conduction model. Considering CeO2 as the major initiator, the size distribution with the power law model is determined from the damage probability statistics. To verify the accuracy of the size distribution, the ion output scaling with depth for the inclusion element is obtained with the secondary ion mass spectrometer. For CeO2 particulates in size of the depth interval with ion output satisfied in the negative exponential form, the corresponding density is consistent with that of the identical size in the calculated size distribution. This coincidence implies an alternative method for the density analysis of photoactive imperfections within optical components at the semi-quantitative level based on the laser damage tests.
The laser-induced damage of optical components has been the main factor to further improve operation stability, output power, and beam quality in high-power laser systems. The level of current damage resistance for ultraviolet laser irradiation suggests that the extrinsic defects are still the main damage precursors. Previously tremendous researches have revealed that the defects are divided into photoactive imperfections, cracks or scratches, etching residues hidden in the subsurface of optics, which initiate extrinsic damage[1] and material modification[2] in the nanosecond regime. However, the low density of the nanometric imperfections embedded in the subsurface obscures the identification.
To understand the underlying defect characteristics, various statistical models (Dirac,[3] power law,[4] Gaussian law,[5] etc.) of defect ensemble are proposed to fit the experimental damage probability curve. The thermal conduction model is also applied for a given class of defects to correlate the defect size distribution and damage probability curve.[6] Nevertheless, the arbitrarily formed threshold distribution fitting was just purposed to highlight the potential candidates and give a plausible explanation for the real physical meaning. In our essay, the thermal-coupling damage model is expanded to validate the defect ensembles and size distribution buried in the subsurface layer, which suggests an alternate approach to probing the density of photoactive defects.
In this study, a synthetical model is used to identify the size distribution of ceria inclusions embedded in the subsurface of polished fused silica, considering the CeO2 specie as the major damage initiator. In Subsection
For the laser-induced damage in the ultraviolet regime, the strong absorption of laser energy for the photo-active defect results in a dramatic temperature increase, melting of the surrounding matrix, phase explosion, and severe surface modification in steps. Especially for thermal-coupling damage, the melting point of the surrounding matrix is usually regarded as the benchmark of damage occurrence.
In the current high-power laser facility, the fused silica substrate serves as the most extensive optical components. Laser damage typically takes place on the rear surface of the fused silica optics.[7] Associated with the polishing process, the CeO2 particulates are introduced as the composition of the polishing slurry[8] and are regarded as the main damage precursors embedded in the subsurface layer. To verify the methodology of our work, we choose the fused silica substrate as the study object to determine the size distribution of the CeO2 inclusions.
Under ultraviolet laser irradiation, the absorption parameter of the spherical defect is reckoned with the Mie theory. The power absorbed by a single ceria defect can be calculated using the following description:
 |
Since the size of defects is of two orders of magnitude smaller than that of the damage pits, the defect is just treated as the seed for the damage explosion.[11] The various sizes of defects indicate the different laser fluence strengths required to reach the critical point. When the interfacial temperature exceeds the melting point of the surrounding matrix, the optical breakdown is initiated. The melting point of the fused silica sample is usually considered as approximately 2000 K.[12] As the photoactive inclusions are of a higher thermal conductivity than the surrounding matrix, the classical approximation is applied for the uniform temperature distributed throughout the spherical inclusion particulates. In that precondition, the evaluation of temperature inside the core can be attained by solving the heat conduction equation[4]
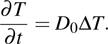 |
 |
The defects in size around tens of nanometers attract extensive concern due to them being the most vulnerable to initiate surface burns. Figure
For a given experimental environment of laser damage tests, the minimum fluence that can initiate the laser damage is well known as the critical fluence corresponding to an identical defect size. Combined with the heat conduction equation, the critical fluence (Gaussian, 8 ns, 355 nm) can be calculated as a function of inclusion size. After the fine fabrication process in the fused silica substrate, the large-sized inclusion can be removed while nanoabsorbers remain in the subsurface layer.
Seen from Fig.
The laser-induced damage for an identical photo-active inclusion is probabilistic under a specific laser fluence because of the inhomogeneous medium contact and random variation of inclusion spatial occupation.[11] Through the probability statistics method, the damage probability versus the fluence curve is plotted to access the performance of the laser-induced damage resistance. We assume that the probability of damage occurrence will increase with the number of defects under the laser shot. Therefore, the differential function of damage probability p(S, F) versus fluence F corresponds to the increment rate of defect amount under the irradiated area S multiplied by the undamaged probability. The relation can be expressed in the following form:
 |
 |
 |
On views of the correlation between laser-induced damage probability curve and defect distribution, a series of optical components are subject to laser irradiation tests to evaluate the internal defect density. If the inclusion is determined as the main type of precursor, the inclusion density inside can be obtained.
For the general optical component irradiated by the laser shot with the central fluence slightly higher than the 0% damage threshold, the damage tends to occur in the spot center. Provided the inclusions disperse with sizes that follow the power-index law surrounded by the silica matrix, the number of identical size a per unit area n(a) can be given by
 |
There exists a lower limit and an upper limit of sizes corresponding to the sensitive defects that can initiate damage. In this manner, the sum of defects under the laser shot N(F) per unit area can be described by the integration of defect numbers with intermediate size as the following expression
 |
Under the specific laser shot, the smaller defects are of a higher amount as the product of a higher areal density and a wider irradiation area. In account of less contribution to the sum and difficulty to reach the critical melting point for big-sized inclusions, this relevant upper size limit can be altered by infinity within tolerant errors in accordance with the Weibull model for damage lifetime estimation.[13] For a better understanding of the rationality of that simplification, we introduce the Weibull statistical model with the joint of laser-induced damage probability versus fluence in the nanosecond regime
 |
The local defect density c(F), derived from Eqs. (
 |
The similar form of power index of the middle and right terms is not coincidental for the correspondence between a− and F, which reflects small defects occupying the main contribution to laser-induced damage. The similarity hints that the inclusion dispersion characteristic can be obtained with a mathematical treatment of the damage probability curve.
For the 1-on-1 laser-induced damage tests conducted on the same batch of samples, the corresponding relation can be deduced, expressed by
 |
 |
Therefore, the synthetical model of the theory mentioned above can be verified with the depth distribution of ion output detected on the second ion mass spectrometer. In Section
A schematic depiction of on-line set-up is shown in Fig.
The silica wafers (Φ50 × 5) as the substrate samples are treated with the ultrasonic cleaning to wipe out the surface contaminations. Belonging to the variety of precursors hidden in the subsurface layer, the inclusion particulates have a weaker damage resistance than the scratches and the etching residue. Previous studies have revealed that the ceria particulates surrounded by the silica matrix are vulnerable to be activated by 355-nm laser. In this way, the prominent property of ceria being the photoactive particulate is a good bonding point in which the density of the ceria particulates can be reduced from the damage probability curve. In the experiments, the same batch of six silica wafers is divided equally into two series separately for damage tests and SIMS detection.
In the damage experiments of the 355-nm laser, the quantitatively similar results are found for the first series of samples. For one sample of the first batch, the fitting curve of damage probability versus fluence is plotted as shown in Fig.
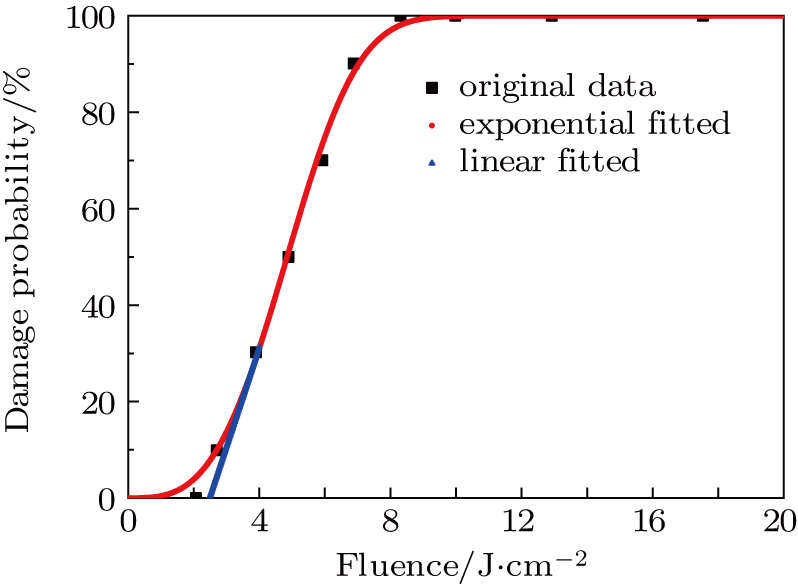 | Fig. 4. (color online) Experimental damage probability curve as a function of fluence in the case of the surface of fused silica including inclusion particles. |
The resistance performance of the first series against high-power laser irradiation can be estimated with the fitting parameters m and c0. The two parameters are separately called the quality factor and defect density coefficient, respectively. In general, the quality factor m characterizes the level of damage initiated by passive defects, and the damage site appears closer to the beam center for a higher m. Meanwhile, the defect density coefficient c0 corresponds to the probability of damage occurring with a relatively low threshold. The more detailed comparative experiment can be adopted for a thorough discussion in the further study on extrapolated applications.
It has been previously determined that, in general, only small-sized defects are buried inside after refined fabrication of the fused silica substrate. Due to the negligible contribution of large-sized defects, only the radius range below 60 nm is applied to the numerical fitting for formula (
 | Fig. 5. (color online) Size versus threshold curve (red) fitting with the original in Fig. |
The measurement of inclusion size-distribution is of significant essence to access the material performance such as processing accuracy, laser resistance and attenuation coefficient of optical transmittance. The inclusion particulates, scratches and other imperfections hidden in the subsurface layer can serve as the laser-induced and mechanical damage source.
The details of the damage precursors can promote the comprehension of the subsurface layer. For a clearer picture, the semi-quantitative density of damage precursors can be measured through the extrinsic damage data in our mathematical methodology. To realize that point, the power index k and coefficient N0 for the defect density distribution should be calculated using Eq. (
The distribution of inclusion density with radius presented in Fig.
 | Fig. 6. Density distribution of different sizes extracted from our model for CeO2 particulates buried in fused silica surface. |
It can be assured that the interval (8.18 nm~ 26 nm) of the inclusion density is reliable directly due to the nature of the extrinsic damage caused by the laser-inclusion interaction. The most sensitive size of defects vulnerable to be laser-ablated perch on not more than tens of nanometers, which agrees with that reported by Kozlowski et al.[16] For the verification of the ceria size interval, a SIMS is applied to detect the depth distribution of the inclusion elements.
To validate the depth profile of the chemical element composition of impurities embedded in the surface and subsurface layer, a Trift II TOF-SIMS is utilized to monitor the entire mass spectrum with a ppm or ppb detection accuracy level. Before the detection, all the samples were cleaned by the deionized water to remove the surface contaminants from the surrounding environment. The scanning area of test point is 100 μm × 100 μm, where a rectangular flat-bottomed pit is caused by the bombardment of Ga ions source on the sample surface with a beam energy of 25 KeV. The ion output rate of the impurity element can be converted into a depth distribution in consideration of a stable depth etching rate for the SIMS.
Due to the unrealized calibration for the impurity element, only the relative density can be confirmed from the ion output with the SIMS. The depth distribution of the impurity ion production is illustrated in Fig.
In Fig.
In this study, a synthetical model of the size distribution of inclusion particulate buried in a fused silica substrate has been validated with laser-induced damage tests. The absorptivity coefficient of the ceria particulate surrounded by the fused silica and the assembly effect on the laser-induced damage threshold are determined to evaluate the performance of the damage resistance. The net defect amount under the laser exposure is obtained as the incoherent addition of individual defect numbers of different radii. Therefore, the semi-quantitative density distribution of ceria inclusion is realized with the numerical fitting of the laser-induced damage data. The specific density of the 10nm-sized particulates is verified with the linear interval of the logarithmic ion output with the secondary mass spectroscopy. Furthermore, the model can be modified and developed in extensive appliances for a wider range of optics and can even support a low-cost and indirect irreducible method to probe the density of photo-reactive defects.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] |





