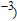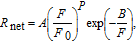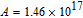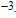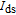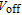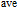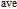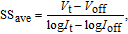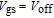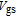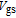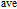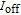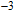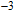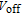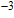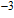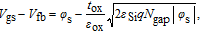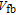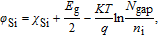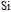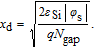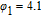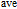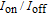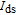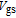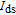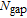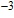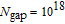1. IntroductionAs the feature size is being scaled down, metal-oxide-semiconductor field-effect transistors (MOSFETs) are facing serious problems. The short-channel effects are one of the most intractable challenges. Because of thermodynamic restrictions, the subthreshold swing (SS) of MOSFET devices must have a minimum value of 60 mV/dec at room temperature. This causes high power dissipation. Tunnel field-effect transistors (TFETs) have been attracting much attention because of their new operating mechanism. The TFETs are driven by band-to-band tunnelling (BTBT), and their SS values are no longer limited to 60 mV/dec; thus, the power consumption can be reduced greatly.[1–5] However, the BTBT mechanism inevitably causes the on-state current of TFETs to be lower than that of MOSFETs by approximately two to four orders of magnitude, limiting the applications of TFETs.[6–11] In addition, contrary to the theoretical prediction, it has been shown experimentally that the SS values of many fabricated TFET devices are much higher than 60 mV/dec.[12–14] Therefore, new channel materials and innovative device structures, such as narrow band-gap materials,[15–17] green FETs,[18] multi-gate TFETs,[19–21] and line TFETs (LTFETs)[22] have been developed to overcome the shortcomings of the TFETs. On one hand, compared to bare Si TFETs, the Ge- and SiGe-channel TFETs have been verified to be potential candidates because of the higher tunnelling rates resulting from the narrow band gaps of Ge.[23–27] On the other hand, many investigations have shown that the LTFETs perform well in terms of the on-state current because of the enlarged tunnelling area.[28–30] However, both suffer from relatively large off-state leakage currents, which degenerate the on/off current ratio. Previously, a heteromaterial-gate (HMG) structure had been proposed and applied to the design of point TFETs to improve their device performance by energy-band profile modulation.[31,32] Few studies have also reported the implementation of the HMG configuration in LTFETs.
In this work, a novel Si/Ge heterojunction LTFET device combined with a symmetric HMG structure is proposed and investigated through two-dimensional (2D) numerical simulations. The results show that the HMG LTFET has much lower off-state currents and superior subthreshold characteristics compared to the traditional single-material-gate (SMG) LTFETs. The lateral energy-band modulation effect induced by the HMG is examined in detail. The work-function mismatch of the HMG has significant impacts on the off-state leakage current and subthreshold characteristics, because of the modulation of the degree of depletion in the gap region. To achieve better performance, the dopant type and doping concentration in this region are also optimized considering the theoretical calculations for the width of the depletion layer. All numerical simulations are carried out using Sentaurus TCAD (Synopsys, San Jose, CA).[33]
2. Device structureFigure 1(a) and 1(b) show the cross-sectional views of a conventional SMG LTFET and the proposed HMG LTFET, respectively. The source/pocket junction is the main region where vertical BTBT occurs in the on state, and the gap region connects the pocket and drain regions. The lengths of the pocket and gap regions are 20 nm and 5 nm, respectively, and both are 5 nm thick. The source is B-doped (1019 cm
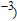 Ge. The pocket, gap, and drain regions are all abrupt P-doped Si with doping concentrations of 1017 cm
Ge. The pocket, gap, and drain regions are all abrupt P-doped Si with doping concentrations of 1017 cm
 , 1015 cm
, 1015 cm
 , and 1020 cm
, and 1020 cm
 , respectively. The metal gate of the proposed HMG LTFET is composed of one pocket gate and two symmetrical gap gates; the pocket gate in the pocket region is M1 with a fixed work function of φ
1, and the gap gate in the gap region is M2 with a tuneable work function of φ
2. Hence, the proposed HMG LTFET is equivalent to a series connection of a vertical tunnelling junction controlled by M1 and a lateral n-type junctionless transistor (JLT) gated by M2.[34] HfO2 with a thickness of 2 nm serves as the gate oxide. The main physical model used to describe the operating principle of this proposed LTFET in the simulation is the dynamic non-local BTBT model, which offers an analytical expression for the tunnelling rate using the Kane model[33]
, respectively. The metal gate of the proposed HMG LTFET is composed of one pocket gate and two symmetrical gap gates; the pocket gate in the pocket region is M1 with a fixed work function of φ
1, and the gap gate in the gap region is M2 with a tuneable work function of φ
2. Hence, the proposed HMG LTFET is equivalent to a series connection of a vertical tunnelling junction controlled by M1 and a lateral n-type junctionless transistor (JLT) gated by M2.[34] HfO2 with a thickness of 2 nm serves as the gate oxide. The main physical model used to describe the operating principle of this proposed LTFET in the simulation is the dynamic non-local BTBT model, which offers an analytical expression for the tunnelling rate using the Kane model[33]
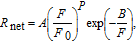 | (1) |
where

is the electron BTBT generation rate in a uniform electric field.
F represents the electric field with a default value
F
0 of 1 V·cm

.
P is 2.5 for indirect tunnelling.
A and
B are variables given by
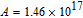
cm
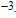
s

and

V·cm

in this work, as calibrated using previous experimental data.
[35] In addition, the Shockley–Read–Hall (SRH) and Auger recombinations are involved. In view of the high doping concentrations in the drain regions, the band-gap narrowing model and the Fermi statistics are also employed. The lateral transport of the carriers is described by the doping-dependent mobility model.
3. Results and discussionThe transfer characteristics of our proposed HMG LTFET are compared with those of the SMG LTFETs at
 , in Fig. 2. The gate work function of the SMG LTFET was set to two different values of 4.1 eV and 4.5 eV, which were the values of φ
1 and φ
2 of the HMG LTFET. As expected, the shapes of the two
, in Fig. 2. The gate work function of the SMG LTFET was set to two different values of 4.1 eV and 4.5 eV, which were the values of φ
1 and φ
2 of the HMG LTFET. As expected, the shapes of the two
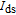 –
–
 curves were mostly identical for the SMG devices. The difference in the gate work functions was evident only in the shift in the onset voltage, which was marked as
curves were mostly identical for the SMG devices. The difference in the gate work functions was evident only in the shift in the onset voltage, which was marked as
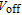 ,[31] indicating the switching of the transistor from the off state to the on state. However, for the HMG LTFET, the introduction of the HMG configuration made a big difference, achieving several advantages simultaneously: the off-state leakage current was lower by approximately three orders of magnitude, the SS was smaller, and no degradation was observed in the on-state current. The inset shows the point SS, which can be calculated as
,[31] indicating the switching of the transistor from the off state to the on state. However, for the HMG LTFET, the introduction of the HMG configuration made a big difference, achieving several advantages simultaneously: the off-state leakage current was lower by approximately three orders of magnitude, the SS was smaller, and no degradation was observed in the on-state current. The inset shows the point SS, which can be calculated as
 and which varies with the increasing drain current. It can be seen that the proposed HMG LTFET has the minimum point SS at approximately 10 mV/dec.
and which varies with the increasing drain current. It can be seen that the proposed HMG LTFET has the minimum point SS at approximately 10 mV/dec.
The enhanced performance can be explained further by the change in the energy band diagram of the HMG LTFET in Fig. 3.
 was maintained at 0.6 V and
was maintained at 0.6 V and
 was assigned several values to represent the different operating modes of the device. When
was assigned several values to represent the different operating modes of the device. When
 , both the SMG and HMG LTFETs were in the off state and the drain leakage current was primarily from the lateral electron drift–diffusion. However, the work function of the gap gate,
, both the SMG and HMG LTFETs were in the off state and the drain leakage current was primarily from the lateral electron drift–diffusion. However, the work function of the gap gate,
 , was higher than that of the pocket gate, φ
1, which pulled up the energy band in the gap region, resulting in a maximum conduction band (
, was higher than that of the pocket gate, φ
1, which pulled up the energy band in the gap region, resulting in a maximum conduction band (
 ). Thus, a local electron potential barrier was formed, leading to a significant reduction in the off-state leakage current.
). Thus, a local electron potential barrier was formed, leading to a significant reduction in the off-state leakage current.
When a positive
 larger than
larger than
 was applied to the gate, the two SMG LTFETs and the HMG LTFET were in the on state. The vertical tunnelling from the source to the pocket was dominant, and the tunnelling direction was perpendicular to the surface plane of the gate oxide. Because the energy band in the vertical direction was controlled by M1, the SMG and HMG LTFETs with
was applied to the gate, the two SMG LTFETs and the HMG LTFET were in the on state. The vertical tunnelling from the source to the pocket was dominant, and the tunnelling direction was perpendicular to the surface plane of the gate oxide. Because the energy band in the vertical direction was controlled by M1, the SMG and HMG LTFETs with
 had similar band profiles in this direction. Therefore, the difference in their drain currents was mainly caused by the modulated lateral JLT. The effect of the applied positive
had similar band profiles in this direction. Therefore, the difference in their drain currents was mainly caused by the modulated lateral JLT. The effect of the applied positive
 on the energy band contends with that of the higher work function of the gap gate. When the positive
on the energy band contends with that of the higher work function of the gap gate. When the positive
 is relatively low (e.g.,
is relatively low (e.g.,
 V), the raising of the energy band induced by the gap gate is dominant; therefore, the conduction band of the HMG device will be higher than that of the SMG device. However, when
V), the raising of the energy band induced by the gap gate is dominant; therefore, the conduction band of the HMG device will be higher than that of the SMG device. However, when
 is high enough (e.g.,
is high enough (e.g.,
 , as shown in Fig. 3), the energy band of HMG LTFETs would be pushed down to a level lower than that of the SMG devices. In this case, the drain current of the HMG LTFET can surpass that of the SMG LTFET, with increase in
, as shown in Fig. 3), the energy band of HMG LTFETs would be pushed down to a level lower than that of the SMG devices. In this case, the drain current of the HMG LTFET can surpass that of the SMG LTFET, with increase in
 .
.
To gain insight into the dependence of the work-function mismatch, a HMG LTFET with different gap-gate work functions is also studied, and the transfer characteristics are presented in Fig. 4(a). In the simulations, the values of φ
2 are varied from 3.7 eV to 4.7 eV in increments of 0.2 eV, while φ
1 is kept unchanged at 4.1 eV. The simulated results show that this variable has a remarkable influence on the performance of the HMG device. It can be seen intuitively that a lower work function of the gap gate causes deterioration in the SS
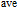 and
and
 . Here, SS
. Here, SS
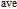 is defined as the average subthreshold swing, which can be expressed as:[36]
is defined as the average subthreshold swing, which can be expressed as:[36]
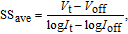 | (2) |
where

is extracted as the drain current at
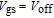
.

is defined as the gate voltage at which the drain current

A/

m.
On one hand, when φ
2 was less than φ
1, the smaller φ
2 led to a lower energy band in the gap region; thus, a lower barrier height for electrons for drift–diffusion could cause a higher
 . However, this reduction in the band energy was favourable for boosting the drain current in the on state. Under a positive gate voltage, the lateral JLT was turned on. In this case, this JLT played the role of a series resistor, whose value was primarily adjusted by M2. The electron density in the surface of this region became larger as φ
2 decreased, making this region a relatively lower resistance channel, and the on-state current was enhanced. Nevertheless, the discrepancy in the on-state current was very slight as
. However, this reduction in the band energy was favourable for boosting the drain current in the on state. Under a positive gate voltage, the lateral JLT was turned on. In this case, this JLT played the role of a series resistor, whose value was primarily adjusted by M2. The electron density in the surface of this region became larger as φ
2 decreased, making this region a relatively lower resistance channel, and the on-state current was enhanced. Nevertheless, the discrepancy in the on-state current was very slight as
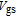 increased. On the other hand, if φ2 was larger than φ
1, the lateral JLT was in the off state under negative
increased. On the other hand, if φ2 was larger than φ
1, the lateral JLT was in the off state under negative
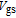 , and the leakage current was generated at the bottom of the channel, i.e., the gap region. In this case, the gap region was depleted and the width of the depletion layer increased as φ
2 increased. Therefore, there was a minimum
, and the leakage current was generated at the bottom of the channel, i.e., the gap region. In this case, the gap region was depleted and the width of the depletion layer increased as φ
2 increased. Therefore, there was a minimum
 when the gap region became fully depleted with a critical value of φ
2, and it could not be reduced further even when a higher φ
2 was adopted. In addition, the excessive increase in φ
2 was detrimental to the on-state current because of the lateral local potential barrier that was formed.
when the gap region became fully depleted with a critical value of φ
2, and it could not be reduced further even when a higher φ
2 was adopted. In addition, the excessive increase in φ
2 was detrimental to the on-state current because of the lateral local potential barrier that was formed.
Figure 4(b) shows the SS
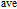 and
and
 ratio as functions of φ
2 for the simulated HMG LTFETs.
ratio as functions of φ
2 for the simulated HMG LTFETs.
 was extracted as the drain current at
was extracted as the drain current at
 and
and
 . Both of them change significantly when φ
2 is lower than 4.3 eV. The
. Both of them change significantly when φ
2 is lower than 4.3 eV. The
 ratio increases and SS
ratio increases and SS
 decreases because of the decreasing
decreases because of the decreasing
 . However, both of them change in an opposite manner when φ
2 is increased further, which is because
. However, both of them change in an opposite manner when φ
2 is increased further, which is because
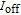 tends to saturate whereas
tends to saturate whereas
 reduces.
reduces.
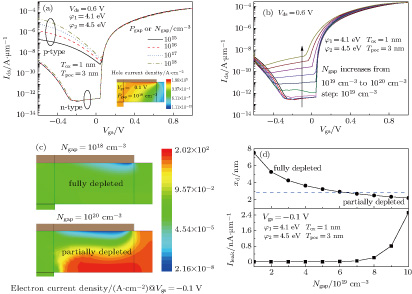
In addition to the work-function mismatch, the dopants in the gap region were also predicted to influence the performance of the HMG LTFET. It needs to be pointed out that the thicknesses of the gate oxide and gap region also have impacts on the device characteristics. The former affects the capability of gate control over the channel and the latter determines the leakage current in the off state. In this section, we modify these two parameters to further highlight the modulation effect of the gap gate on the gap region. The transfer characteristics with various dopant types and doping concentrations in the gap region of the HMG LTFET with a 3-nm-thick gap region and a 1-nm-thick gate oxide are depicted in Fig. 5(a). Because the same structure is used for the pocket region and the gate stack on top of it, the onset voltage and on-state current of all simulated devices are almost the same. The obvious difference is reflected in the off state, which depends primarily on the gap region. The HMG LTFETs with an n-type gap have a flat ambipolar window in a certain range of negative gate voltages, while those with a p-type gap transform immediately from forward operation to an ambipolar state. The inset shows the simulated hole current density of an HMG LTFET with a p-type (1018 cm
 gap region at
gap region at
 . In this case, the p-type gap was accumulated and the hole drift–diffusion current was collected in the source region. As
. In this case, the p-type gap was accumulated and the hole drift–diffusion current was collected in the source region. As
 became more negative, a hole BTBT process from the drain to the gap region was induced by the higher energy band in the gap region, which also contributed to the ambipolar current. This caused the
became more negative, a hole BTBT process from the drain to the gap region was induced by the higher energy band in the gap region, which also contributed to the ambipolar current. This caused the
 –
–
 curves of the HMG LTFET devices with a p-type gap to appear in the form of a ‘V’.
curves of the HMG LTFET devices with a p-type gap to appear in the form of a ‘V’.
For transistors with an n-type gap, it was noticeable that a relatively low doping level varying from 1015 cm
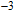 to 1018 cm
to 1018 cm
 caused almost no difference in the off-state current. However, when the doping level was changed from 1019 cm
caused almost no difference in the off-state current. However, when the doping level was changed from 1019 cm
 to 1020 cm
to 1020 cm
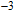 , the off-state current increased dramatically, as can be observed in Fig. 5(b). Because
, the off-state current increased dramatically, as can be observed in Fig. 5(b). Because
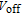 was larger than zero, the n-type gap region was in a depleted state under the low negative
was larger than zero, the n-type gap region was in a depleted state under the low negative
 , and the width of the depletion layer decreased with increasing doping concentration. Figure 5(c) presents a comparison of the electron current densities for the gap region with n-type doping of 1018 cm
, and the width of the depletion layer decreased with increasing doping concentration. Figure 5(c) presents a comparison of the electron current densities for the gap region with n-type doping of 1018 cm
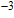 and 1020 cm
and 1020 cm
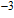 at
at
 . The distributions of electron current clearly show that the gap region is fully depleted with a relatively low doping level and that it becomes partially depleted as the doping level becomes sufficiently high.
. The distributions of electron current clearly show that the gap region is fully depleted with a relatively low doping level and that it becomes partially depleted as the doping level becomes sufficiently high.
To quantitatively estimate the width of the depletion layer, we use the depletion approximation. The gate voltage equation for the lateral JLT can be expressed as follows:
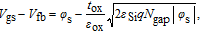 | (3) |
where
q is the charge of the electron,
φ

is the surface potential, and

is the thickness of the gate oxide layer.
ε

and
ε

are the dielectric constants of the gate oxide and Si, respectively.

is the doping concentration of the gap region, and

is the flat band voltage. Under the assumption that there is no trap charge in the gate oxide,
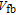
is equal to the difference in the work functions between M2 and Si (gap region), that is,

, where
φ

is the work function of Si, which can be calculated as follows:
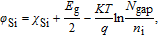 | (4) |
where
χ
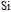
is the electronic affinity of Si, and

expresses the intrinsic carrier concentration.

is the band gap of Si.
K is the Boltzmann constant and
T is the temperature.
S If the impact of

is neglected, the width of the depletion layer

in the gap region is:
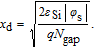 | (5) |
Figure 5(d) shows the calculated
 and leakage current (
and leakage current (
 of the HMG LTFETs extracted from Fig. 5(b) at
of the HMG LTFETs extracted from Fig. 5(b) at
 . Based on the calculated results, the 3-nm-thick gap region was fully depleted when
. Based on the calculated results, the 3-nm-thick gap region was fully depleted when
 was less than
was less than
 cm
cm
 , and accordingly,
, and accordingly,
 was almost unchanged in this range. When
was almost unchanged in this range. When
 increased, the channel of the JLT became partially depleted. The electrons could drift and diffuse at the bottom of this region, and the non-depleted region for electrons to flow broadened with increasing
increased, the channel of the JLT became partially depleted. The electrons could drift and diffuse at the bottom of this region, and the non-depleted region for electrons to flow broadened with increasing
 , which caused the
, which caused the
 to rise sharply. This dependence of the off-state performance on the channel doping concentration was observed in some previous researches concerning JLTs.[37–39] These results indicated that, to suppress the off-state leakage current, the gap-gate material and n-type doping level in the gap region should be simultaneously optimized to make the gap region fully depleted.
to rise sharply. This dependence of the off-state performance on the channel doping concentration was observed in some previous researches concerning JLTs.[37–39] These results indicated that, to suppress the off-state leakage current, the gap-gate material and n-type doping level in the gap region should be simultaneously optimized to make the gap region fully depleted.