† Corresponding author. E-mail:
‡ Corresponding author. E-mail:
Project supported by the National Key Research and Development Plan of China (Grant No. 2016YFA0200402), the National Natural Science Foundation of China (Grants Nos. 11574369, 11574368, 91323304, 11174362, and 51272278), and the FP7 Marie Curie Action (project No. 295208) sponsored by the European Commission.
Some color centers in diamond can serve as quantum bits which can be manipulated with microwave pulses and read out with laser, even at room temperature. However, the photon collection efficiency of bulk diamond is greatly reduced by refraction at the diamond/air interface. To address this issue, we fabricated arrays of diamond nanostructures, differing in both diameter and top end shape, with HSQ and Cr as the etching mask materials, aiming toward large scale fabrication of single-photon sources with enhanced collection efficiency made of nitrogen vacancy (NV) embedded diamond. With a mixture of O2 and CHF3 gas plasma, diamond pillars with diameters down to 45 nm were obtained. The top end shape evolution has been represented with a simple model. The tests of size dependent single-photon properties confirmed an improved single-photon collection efficiency enhancement, larger than tenfold, and a mild decrease of decoherence time with decreasing pillar diameter was observed as expected. These results provide useful information for future applications of nanostructured diamond as a single-photon source.
Diamond is an important material with many outstanding properties that serve as the basis for its applications in biology, high-pressure science, and other fields.[1–7] Benefiting from its abundant naturally existing or artificially induced color centers, the material now draws more and more interest from researchers globally for its heretofore unobserved physical and optical properties and promising applications in areas such as single-photon source, high-sensitivity sensors, and information processing.[8–20] Of particular interest is the electron spin of nitrogen vacancy (NV) centers in diamond, which can be initialized, coherently controlled, and read out at room temperature.[11] The robust spin coherence[13] and optical addressability via spin-dependent orbital transitions[14] strongly suggest that such systems have great potential in applications ranging from quantum information processing[15–18] to nanoscale magnetic field sensing.[21–24]
However, bulk diamond crystals have the disadvantage of low photon out-coupling, that is, the total reflection effect at the diamond–air interface results in tremendous loss of fluorescence photon counting rate. To address this problem, theoretical and experimental works have been performed to investigate the effects of size and geometry on the single-photon collection efficiency of NV-embedded diamond structures. In particular, different micro/nano structures like hemispheres and nanowires have been fabricated out of diamond substrates to improve the in- and out-coupling of photons, to facilitate the manipulation of the light–matter interactions,[25–27] and for more efficient excitation, higher collection efficiency, and single-photon flux.[28] For size effect studies, thin and high-aspect-ratio nanowires covered with a graphic or carbonaceous shell have been obtained through chemical vapor deposition (CVD).[29] Diamond fibers with various diameters were fabricated by a top-down method and the best shape for diamond nanowires was predicted by simulations. The optical coupling of the NV center emission (at λ = 637 nm) to diamond nanowire has been modeled using FDTD simulations.[30] The best coupling efficiency was found in nanowires with diameters between 180 nm and 220 nm.[31,32] In addition, in recent work, the effect of a nanowire's morphology on single-photon collection efficiency was reported for a conical nanowire, and a net photon flux exceeding 1.5 × 106 s−1 was achieved.[32] Nevertheless, optimized fabrication approaches for large scale diamond micro-/nano-structures with tunable geometry, size, and distribution are still much needed.[33]
For the work reported in this paper, we adopted a two-stage technique of electron beam lithography (EBL) followed by induction coupled plasma (ICP) reactive ion etching (RIE) to fabricate diamond nanopillars of various sizes and top shapes. Thin diamond nanopillars with diameters down to 45 nm and aspect ratios up to 20 were prepared. The nanopillar top end geometry evolution process during etching was studied systematically. The dependency between the fluorescence photon collection rate of the NV center and the nanopillar's diameter was also probed. Measurement of the single-photon count rate indicates an enhancement of about tenfold in photon collection efficiency compared with the un-sculpted diamond crystal. The g(2)(τ) and Ramsey fringe measurements show that the RIE processing affects neither the single-photon emission nor the coherence properties. The size effect was examined and the underlying mechanism is discussed.
Two alternative kinds of fabrication processes, HSQ negative resist (Fig.
 | Fig. 1. Top-down fabrication of diamond nanostructure arrays by electron beam lithography related techniques: (a) HSQ negative resist approach, (b) PMMA positive resist approach. |
For the PMMA approach, again, a layer of 300 nm PMMA was spin-coated on a cleaned diamond surface. Then circle patterns were exposed with EBL and developed. Thereafter, Cr was deposited, 90 nm thick, with a thermal evaporation system, followed by lift-off in acetone to obtain circular Cr masks. Unlike the first approach, rather than using the developed resist as the mask, here we used a pattern transfer process, metal deposition, and lift-off. After RIE processing, the remaining Cr was removed to leave diamond nanopillars.
The measurements of fluorescence scanning and single-photon count rate were carried out on a home-built laser scanning confocal microscope system that can detect single-photon fluorescence with sub-micrometer precision. During measurement, a 532-nm continuous wave laser beam was switched on and off by an acoustic optical modulator (AOM); an X–Y galvanometer was used to control the scanning of the laser spot before it was directed to the sample through a microscope objective. The spin state-dependent fluorescence of the NV center was collected by the same objective, which was then filtered by a 532 nm notch and a 650 nm long path. After that, the weak light signal was translated into an electronic pulse signal by a single-photon counting module and was subsequently counted by a pulse counter or routed to a Hanbury–Brown and Twiss detection system to record the second order intensity correlation function g(2)(τ).
Diamond nanopillar arrays of various diameters and periods have been prepared with the HSQ approach. First of all, the effect of the period of the patterns was examined. For a particular diameter, patterns with the period set twice, threefold, fivefold, and tenfold were prepared. For the developed masked cylinders of small diameter, we found that only arrays of small periods can stand straight. Specifically, pillars with diameter of 50 nm or 80 nm easily “fall down” on the substrate when the period is larger than three times the diameters. Figure
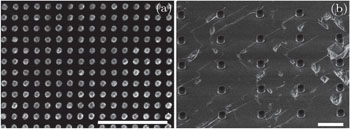 | Fig. 2. Pillars prepared with the HSQ negative resist approach: (a) diameter 50 nm, period 100 nm; (b) diameter 300 nm, period 1.5 μm. The scale bar is 2 μm. |
With the PMMA approach, several Cr-masked column arrays of different diameters and different periods were prepared. Arrays of pillars with diameter of 80 nm, period of 160 nm and diameter of 250 nm, period of 500 nm are shown in Fig.
 | Fig. 3. Pillars prepared with the PMMA positive resist approach: (a) diameter 80 nm, period 160 nm; (b) diameter 250 nm, period 500 nm. The scale bar is 2 μm. |
Diamond nanopillar arrays of different diameters and different periods were then prepared in an RIE system employing HSQ (Fig.
Diamond nanopillars prepared with the PMMA approach also have a conical top-end (Fig.
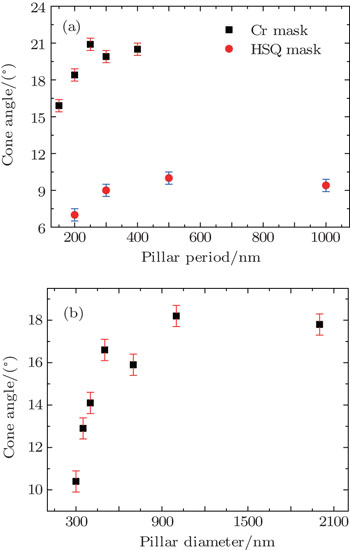
To find out the relationship between the apex angle and the mask material, a more detailed experiment was undertaken. The apex angles of the pillars prepared with both Cr and HSQ masks were measured as shown in Fig.
It should also be noted that the apex angle of the pillars prepared by the HSQ approach has a smaller range of increase − – the maximum value is just half that of those prepared with a Cr mask. Such a difference comes mainly from the initial tomography of the two mask materials. By comparing the HSQ mask results and Cr mask results shown in Figs.
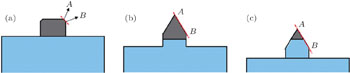
For a better understanding, the apex angle evolution during the etching process was investigated and a simple model was proposed. At first, diamond pillar arrays of different diameters were etched using the PMMA approach in which the Cr mask was used (Fig.
Based on the experimental results discussed above, we here propose a conical top end evolution model of diamond pillars prepared by RIE. The process is roughly divided into three stages (Fig.
The conical shape forms earlier for pillars of smaller diameter than for the thicker ones. The apex angle of the latter keeps increasing while the former one becomes fixed. In this way, larger apex angles can be obtained for thicker pillars, as we discussed with regard to Fig.
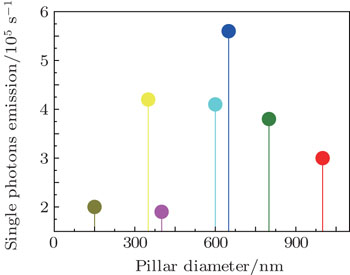
For measuring single-photon properties, pillars with diameter from 150 nm to 1 μm were prepared on a piece of 1 ppm diamond with proper distribution of single NV centers by the HSQ approach. In the confocal scanning imaging process, obvious brighter spots can be picked out, their positions can be identified, and they can be confirmed to represent NV-center emissions. The second order autocorrelation function measurement further verified the single-photon emission property. The relation between the single-photon collection efficiency enhancement and the diameter of the pillar was then studied. Pillar arrays of various diameters were scanned and their single-photon counting rates were compared. The single-photon counting rates of NV centers in pillars with a given diameter vary. We take pillars of 800 nm diameter as an example, the largest counting rate was 3.8×105 counts/s, while the smallest was 2.7×105 counts/s. The inset of Fig.
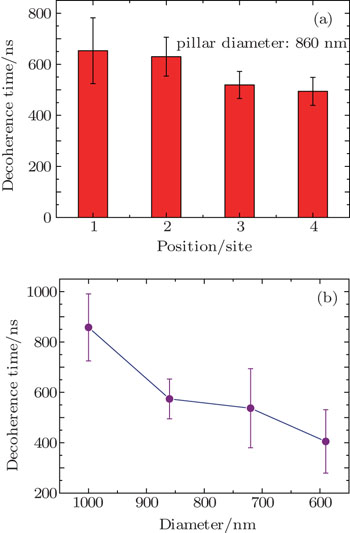
Decoherence time 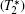
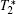

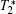
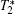
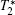
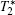
We show effective fabrication of diamond nanopillars of varied diameters with both HSQ and PMMA approaches using RIE. Ultra-thin pillars of 45 nm in diameter and high/diameter ratio of 20 were obtained with the HSQ approach. We find that a conical top end can be formed and the apex angle changes with the mask material, the mask period, and the diameter of the pillars. A facet-etching model is then proposed to explain the top shape evolution. The size dependent single-photon collection efficiency of NV centers buried in the diamond pillars was investigated. It was found that the best enhancement exceeded tenfold. The measurement also shows variation of the decoherence time of pillars with the same diameter, which might be correlated with the shape of every pillar and the random distribution of the site position of each NV center in different pillars. However, a mild decrease of decoherence time with reduction of pillar diameter has been observed, which is as expected. Our results could provide very useful information for future applications of nanostructured diamond as single-photon sources.
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 | |
| 18 | |
| 19 | |
| 20 | |
| 21 | |
| 22 | |
| 23 | |
| 24 | |
| 25 | |
| 26 | |
| 27 | |
| 28 | |
| 29 | |
| 30 | |
| 31 | |
| 32 | |
| 33 | |
| 34 |