† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant Nos. 11305032, 11305028, 11375163, and 11275039) and the Scientific Foundation of Ministry of Education of China (Grant No. N130405008).
A one-dimensional hybrid model was developed to study the electrical asymmetry effect (EAE) caused by the fourth-order harmonic in a dual-frequency capacitively coupled Ar plasma. The self-bias voltage caused by the fourth-order frequency changes periodically with the phase angle, and the cycle of self-bias with the phase angle is π/2, which is half of that in the second-order case. The influence of the phase angle between the fundamental and its fourth-order frequency on the ion density profiles and the ion energy distributions (IEDs) were studied. Both the ion density profile and the IEDs can be controlled by the phase angle, which provides a convenient way to adjust the sheath characters without changing the main discharge parameters.
Capacitively coupled plasmas (CCP) are of vital importance in materials processing such as etching and deposition in the semiconductor industry.[1,2] In the industrial processes, throughput is determined by the ion flux, etching and deposition processes are controlled by the ion energy, therefore, the independent control of the ion flux and ion energy is necessary for these applications.[3] However, separate control of ion flux and ion energy is difficult in the single frequency discharge. In order to overcome this problem, the dual-frequency capacitively coupled plasma (DF-CCP)[4] was proposed to control the ion flux and energy separately. The traditional DF-CCP[4–9] usually has two frequency sources which are applied to one or two electrodes,[4,6,7,9–17] wherein the low frequency source controls the ion energy and angular distributions, while the high frequency source controls the plasma density and ion flux. Although the traditional DF-CCP has been used for a long time, this mode has been investigated and confirmed that it might limit the separate control of the ion flux and energy recently.[18,19]
A novel idea based on a newly discovered electrical asymmetry effect (EAE) was introduced to achieve high-degree separate control of ion flux and energy in dual-frequency capacitively coupled plasmas.[20,21] The two sheaths close to the surface of electrode are electrically asymmetrical by applying a fundamental and a second harmonic to the discharge, even the discharge itself is geometrically symmetric. A DC self-bias develops both in geometrically symmetric and geometrically asymmetry discharges.[20] By changing the phase angle, one can modulate the ion energy distributions according to the linear relationship between DC self-bias voltage and the phase angle Θ. The applying of the second harmonic may lead to a best control of both the ion energy and the ion flux. Recently, the electrical asymmetry effect in DF-CCP discharge has been studied both numerically and experimentally[22,27] and has been analyzed in detail through the analytical model, fluid and particle in cell (PIC) simulations. In particular, Donkó et al.[22] studied EAE operated in the 13.56 MHz and 27.12 MHz in the geometric symmetry discharge. The result confirmed the theoretical prediction of Heil et al.[20] and verified that the separate control of ion flux and energy can be realized through the EAE in an ideal manner. Later, Schulze et al.[23] tested this result in the EAE experiment for the first time. Electron heating in electropositive capacitively coupled plasma has been studied by using experiments, simulations and models.[28–41] For example, Jiang et al.[42,43] developed a PIC/MC model and studied the heating mechanisms in detail. Lisovskiy et al. studied the three discharge modes and the mode transitions in low pressure nitrogen[44–46]. Schulze et al. investigated electrically asymmetric DF-CCP discharges in CF4 by particle-in-cell simulation at different pressures and values of Θ.[47]
In previous studies, a common choice for the two frequencies was fundamental frequency f with its second harmonic 2 f. To achieve a separate control of the ion energy and the ion flux, a large disparity of the two frequencies is needed. Therefore, a higher-order harmonic would be needed in order to achieve both the EAE and the separate control of the ion flux and the energy. In this paper, we choose the fundamental frequency f and its four-order harmonic 4 f. Firstly, an analytic discussion is presented based on the physical model by Heil et al.[20] By using the four-order frequency, the self-bias varies with the phase angle more rapidly, the period abridges from π to π/2. In this case, more data are needed to study the relationship between the phase angle and the self-bias, therefore, in this paper, we study the EAE of Ar plasmas using a one-dimensional fluid/MC hybrid model which can provide an accurate simulation result more efficiently. The concept of a hybrid model[48–51] was proposed in the 1990s. The model consists of two parts which are a fluid model and a Monte Carlo model respectively. The study of the ion energy distributions (IEDs) is quite necessary since the ion flux plays an important role during the surface etching procedure. In particular, we focus on the IEDs striking the electrode, and make a comparison of DC self-bias and IEDs with different phase angles between the two frequencies.
The main contents of this paper are as follows. The analytic physics model is presented in Section 2. The one-dimensional fluid/MC hybrid model for the discharge, the numerical results, and the discussion are given in Section 3, and a brief summary is in Section 4.
The applied RF voltage is
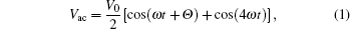
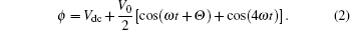
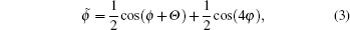
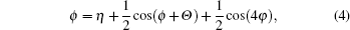
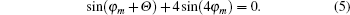
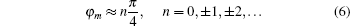

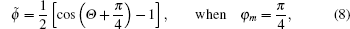

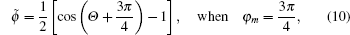

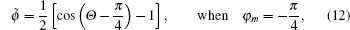

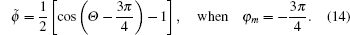
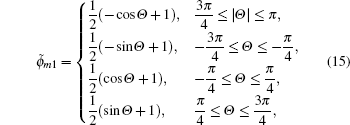
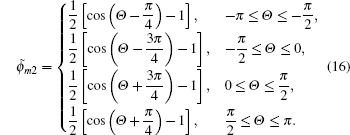
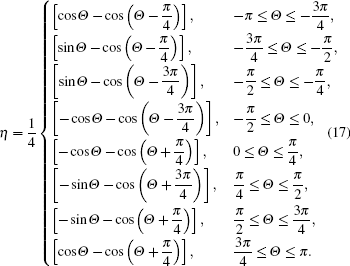
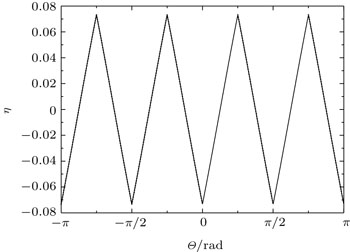
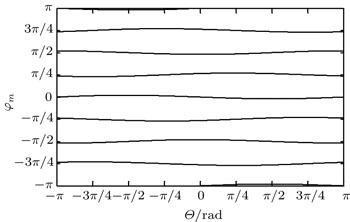 | Fig. 1. Solutions of Eq. ( |
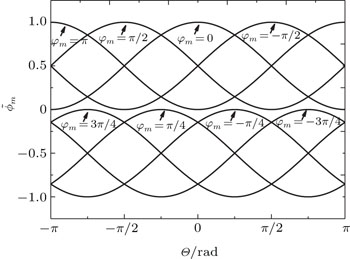 | Fig. 2. The picture of Eqs. ( |
In this section, the hybrid model containing a fluid model and a Monte Carlo model is introduced. The fluid model mainly calculates the physical properties of the bulk plasma in the transport process and the Monte Carlo method is used to compute the ion energy distributions (IEDs) after the collision occurs. This method can not only improve the computational efficiency, but also help to obtain accurate results.
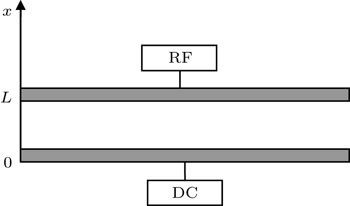
The schematic diagram of the capacitively coupled plasma reactor is shown in Fig.
The fluid model consists of continuity and momentum equations of electrons and ions, the energy balance equation of electrons, and Poisson’s equation. In the discharge process, the collisions between ions and surrounding neutral gases are frequent, therefore, the ion temperature is basically consistent with the neutral gas, and it is unnecessary to solve the energy equation of ions. The drift-diffusion approximation is valid for describing the electron flux and ion flux in the fluid model since the pressure in discharges is not too low. In this mode, the ionization occurs mainly in the region of the bulk plasma, and the ionization does not play an essential role. Therefore, we ignore the secondary electron emission, and the electron flux and the electron energy flux to the electrodes are assumed as follows:
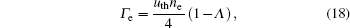
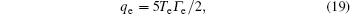
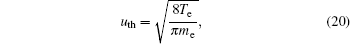
Furthermore, we can describe the behaviors of ions and electrons and the electric potential by the following equations:

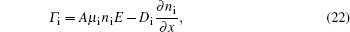


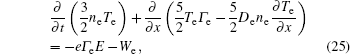
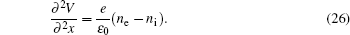
After obtaining the plasma density, the electric field, and other macroscopic quantities in the fluid module, we can trace the trajectories of test particles in the discharge process. The grid step of space in the MC model is Δx = 0.5 × 10−4 m, the time step is one thousandth of the RF period which equals to Δt = 0.25 × 10−10 s, and the velocity is normalized by the factor of Δx/Δt = 0.5 × 10−4/0.25 × 10−10 m · s−1. The motion equation is calculated by Newton’s equation and the collision process is simulated by the Monte Carlo method. The energy and angular distributions of each particle will be recorded when the test particle reaches the designated position. According to the statistical result of the distributions by using a large number of test particles, we can accurately calculate the energy and angle distributions of the electrons, ions, and groups anywhere we want to know. In this paper, for the argon plasma, we assume that the neutral species have a uniform distribution in space with a Maxwellian velocity distribution, and the temperature of neutral gas is the same as that in the fluid model.
For the argon plasma, the collisions of electrons are elastic scattering (e + Ar → e + Ar), excitation (e + Ar → e+Ar*), and ionization (e + Ar → 2e + Ar+). For the ion–neutral collisions, the elastic scattering (Ar+ + Ar → Ar+ +Ar) and the charge exchange collision (Ar+ + Ar → Ar+ Ar+) are included in the present model.
Besides, we use the null-collision method to reduce the computational time. The following equation shows that the collision probabilities for all the particles are independent of the energy and position
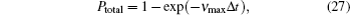
The initial value of the plasma potential is set to 0 V, the discharge pressure is set to P = 50 mTorr, and the voltage applied to the lower electrode is
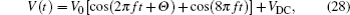
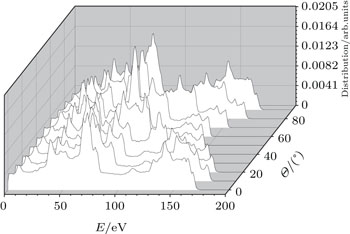
Figure
Figure
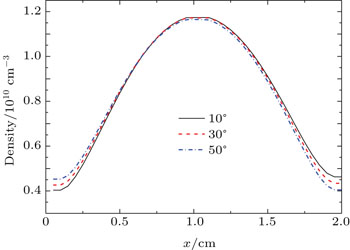 | Fig. 5. The temporally averaged ion density profiles. The phase angles between the first and the fourth harmonics are Θ = 10°,30°,50°. |
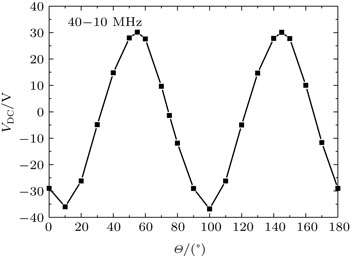 | Fig. 6. The self-bias VDC on the electrode with different phase angles Θ caused by the fourth-order harmonic with V0 = 400 V. |
 | Fig. 7. The self-bias VDC on the electrode with different phase angles Θ caused by the second-order harmonic with V0 = 400 V. |
A comparison of the self-bias between the analytic method result and the hybrid model result is presented in Fig.
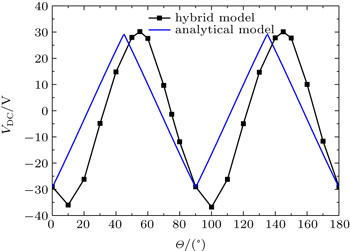 | Fig. 8. The comparison of the self-bias calculated by the analytic method and the hybrid model with V0 = 400 V. |
Figure
In the present paper, an analytical model and a one-dimensional hybrid model have been used to investigate the electrically asymmetric effect in a capacitively coupled argon discharge driven by the basic 10 MHz and its fourth-order frequency 40 MHz. The self-bias which balances the electron and ion flux toward the two electrodes changes with different phase angles between the basic and the fourth-order frequency. Comparing with the second-order frequency 20 MHz, the cycle of self-bias with the phase angle changing from π to π/2 (half of the 10 MHz–20 MHz case), the self-bias voltage varying linearly within each of the π/4 regions, and the influence on the self-bias caused by the fourth-order frequency is relatively small. However, the density profile and the IEDs on the electrode can also be controlled by the phase angle Θ, the max energy, and the high energy peaks in IEDs change simultaneously with the self-bias. This means that the profile of the density and the ion energy on the electrode can also be controlled by fourth-order frequency, which provides an opportunity to adjust the discharge profile in an easy and convenient way.
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 | |
| 18 | |
| 19 | |
| 20 | |
| 21 | |
| 22 | |
| 23 | |
| 24 | |
| 25 | |
| 26 | |
| 27 | |
| 28 | |
| 29 | |
| 30 | |
| 31 | |
| 32 | |
| 33 | |
| 34 | |
| 35 | |
| 36 | |
| 37 | |
| 38 | |
| 39 | |
| 40 | |
| 41 | |
| 42 | |
| 43 | |
| 44 | |
| 45 | |
| 46 | |
| 47 | |
| 48 | |
| 49 | |
| 50 | |
| 51 | |
| 52 | |
| 53 | |
| 54 | |
| 55 | |
| 56 |