† Corresponding author. E-mail:
‡ Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant Nos. 11175075, 11405078, 11474140, 11404152, and 11305083).
There is no available theoretical description of electron transfer from negative projectiles at a velocity below 0.1 a.u. during grazing scattering on insulating surfaces. In this low-velocity range, electron-capture and electron-loss processes coexist. For electron capture, the Demkov model has been successfully used to explain the velocity dependence of the negative-ion fraction formed from fast atoms during grazing scattering on insulating surfaces. For electron loss, we consider that an electron may be transferred from the formed ionic diabatic quasi-molecular state to the formed covalent diabatic quasi-molecular state by the crossing of the potential curves of negative projectiles approaching the surface cations, which can be described by the Landau–Zener two-energy-level crossing model. Combining these two models, we obtain good agreement between the experimental and calculated data for the F−–LiF(001) collision system, which is briefly discussed.
Electron transfer during particle–surface interactions has long been studied because it is closely related to reactive events and catalytic processes at surfaces. From an application perspective, electron transfer between particles and surfaces can be used to determine the elemental composition of a surface layer; i.e., the low-energy ion-scattering (LEIS) technique.
To further illustrate the importance of electron-transfer phenomena at surfaces, let us consider the scattering of atomic particles from insulator surfaces. Souda et al.[1–3] studied the target electronic excitation in low-energy H+ (D+) ions scattering from various ionic-compound surfaces, such as alkali-metal halides and oxides. The resonant tunneling process and energy-level crossing play important roles in the neutralization of H+ ions, whereas the electronic excitation of surfaces is ascribed to the electron-promotion mechanism. Band effects on the neutralization of D+ were later reported by Souda et al.[4] In particular, Winter et al.[5] first described high negative-ion formation for oxygen atoms during grazing scattering from a LiF(100) surface. One year later, Esaulov et al.[6] reported a dramatic increase in H− formation in H+ ion scattering on oxidized Mg and Al surfaces. Subsequently, these authors observed the efficient generation of a high negative-ion fraction when scattering on a MgO(100) crystal surface.[7] In 2011, Winter et al.[8] also investigated the H− fraction on an oxidized NiAl(110) surface and found that the H− fraction was nearly one order of magnitude smaller than that on a LiF(001) surface. It was concluded for both alkali-metal halide and oxide surfaces that the wide band-gaps strongly suppress the electron loss from the formed negative ion back to the ionic surface, resulting in a high negative-ion fraction. However, electron-loss processes related to the high survival of negative ions have not received as much experimental or theoretical attention as electron-capture processes.[7,9–12]
Theoretically, the concept of resonant electron transfer is not appropriate for insulator surfaces with wide band-gaps because the energy-level down shift is small given the image potential effect, Borisov et al.[13,14] proposed that the large energy-level difference between a projectile’s affinity level and the valence band state of a surface can be significantly reduced by the Madelung potential of an ionic surface, which facilitates quasi-resonant electron capture. Based on this concept, the Demkov model[15,16] has been successfully applied to describe the electron-capture probability for negative-ion formation from the active anion site on insulator surfaces at small velocities above the velocity threshold of negative-ion formation (∼ 0.1 a.u.). However, this model does not reproduce the experimental data at relatively high (≥ 0.3 a.u.) or low (v ≤ 0.1 a.u.) velocities. The electron-loss process occurs and has been experimentally observed,[4] but it is not considered in the theoretical model. Recently, some efforts have been devoted to investigating relatively high velocities (≥ 0.3 a.u.), for which the electron tunneling in the repulsive Coulomb field built by both the formed negative ion and the anion site has been considered.[17] However, a quantitative agreement between experiment and theory without adjustable parameters has not yet been achieved, although several different mechanisms[18] have been proposed to qualitatively explain the experimental findings. In contrast, to our knowledge, no explanation has been developed for electron loss at very low velocities (v ≤ 0.1 a.u.), it occurs efficiently on the ionic-surfaces (such as, MgO(100)[7] and LiF(001)[19]). Thus, understanding electron loss at very low velocities is urgently needed.
In this paper, we theoretically calculate the velocity dependence of the negative-ion fraction of negative fluorine ions scattering on a LiF(001) surface with a grazing incident angle of ∼ 1° in the low-velocity range of v ≤ 0.1 a.u. In this range, electron loss, which occurs efficiently at the cation sites of the LiF(001) surface, has been considered to be the main charge-transfer process. We use atomic units throughout this paper, unless otherwise specified.
Before discussing electron loss at cation sites, let us first consider an atom colliding with anion sites on the insulator surface. These anions are regarded as active sites. When the atom approaches the active site, its affinity level decreases significantly because of the Madelung potential effect.[7] The energy defect ΔEC between the affinity level and the valence band state of the surface can be approximated by the following equation:[11,13]

For simplicity, we neglect the first two polarization effects and take into account only the Mott–Littleton contribution. The projectile captures an electron from the anion site and leaves a hole at the site. This electron–hole pair creates the resulting electric dipole moment e

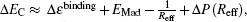
Negative-ion formation via electron transfer from the anion site to the atomic projectile occurs efficiently, and the electron-capture probability Pcap is described by the Demkov model[15,16,24,26]


In our previous study,[17] we introduced electron-tunneling behavior to describe the destruction of formed negative ions at surface anions. For a grazing incident angle of ∼ 1°, the motion of a projectile along the surface plane can be decoupled into parallel and perpendicular motions. As the projectile approaches the surface, the formed negative ion can be destroyed via quantum tunneling of electrons in the repulsive Coulomb field built by both the negative ion and the anion site. Thus, the electron-loss probability is calculated using the Wentzel–Kramers–Brillouin (WKB) barrier penetration probability within the action integral, which is given by[27]


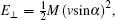
However, the projectile collides not only with the anion sites of the ionic surface but also with the cations. Now, we discuss a series of soft binary collisions between a negative projectile ion and the cation sites where electron transfer may occur as follows:

Based on the energy-conservation requirement, we can simply analyze the electron-transfer process. The conduction band of bulk LiF consists of the 2s, 2p states of Li, and the 3d state of F.[30] According to Refs. [31] and [32], the first-empty band corresponds to a Li+ ion 2s electron and to the conduction band bottom energy level of the LiF(001) surface. This can be simply understood in terms of the shift of the 2s energy level of the free Li atom from –5.4 eV to approximately 2.0 eV[22,23] via the Madelung potential and correlation and exchange effects.[33,34] From Eq. (

Similar to the initial state, we obtain the energy of the final state as follows:

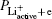
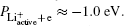
From Eqs. (

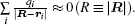

Equation (
According to Ref. [40], if R is less than a critical distance (13.6/εF−)1/2 = 2 a.u., the description of the atomic distribution of electrons becomes invalid. Instead, a molecular characterization must be adopted for the single-electron transition between collision partners. Therefore, equation (
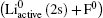
Based on this physical picture, two energy levels crossing according to the Landau–Zener model may be appropriate. The requirements for the Landau–Zener model are as follows.
Here, 2Vtransfer (Rc) = 0.026 a.u. (0.7075 eV) is small relative to most of our projectile energy range. Figure
The well-known Landau–Zener model for a two-state energy level crossing[44,45] describes the electron-loss process between the ionic diabatic quasi-molecular state 


In a diabatic representation,

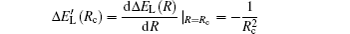
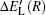
According to Ref. [46], the diabatic representation allows one to calculate the ionic adiabatic quasi-molecular potential 


In the Landau–Zener model, this obviously leads to ΔEadiabatic (Rc) = 2Vtransfer (Rc), which corresponds to the minimum of the adiabatic splitting ΔEadiabatic (R) and represents the non-crossing of the ionic adiabatic quasi-molecular potential by the covalent adiabatic quasi-molecular potential. Additionally, it should be noted that Rc actually reflects the center of the non-adiabatic region in an adiabatic representation.
For a single-electron transition, the semi-empirical formula given in Refs. [40] and [46] is used in the present work for the charge-transfer matrix element 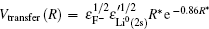


According to Ref. [42], the width ΔR of the transition zone is (4πveffħs/α)1/2, where 
For a single collision of the atom with the active anion site on the surface in the present velocity range, we obtain the single-collision, electron-capture probability along the incoming and outgoing trajectory of the projectile in the electron capture region; i.e.,

In contrast, for a single collision of the F− ion with the Li+ cation site, we obtain the electron-loss probability PLZ(1 − PLZ) P↑ (1 − P↓) + PLZ (1 − PLZ)P↓ (1 − P↑) when the process occurs only along the incoming trajectory of the F− projectile in the electron-loss region. However, if this process occurs only along the outgoing trajectory, the electron-loss probability is as follows: (1 − PLZ)PLZ P↑ (1 − P↓) + (1 − PLZ)PLZ P↓ (1 − P↑), where P↑ = P↓ = 1/2 represents the spin statistic. Consequently, the electron-loss probability throughout the trajectory is

Before moving away from the surface, the incoming negative ion experiences a series of collisions with the active anion and cation sites at a grazing incident angle of α = 1°. After N sequential effective collisions, the final negative-ion fraction P(N) obeys the following first-order, linear, non-homogeneous differential equation

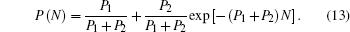
In Fig. 
In Fig.
 | Fig. 2. Negative-ion fractions as a function of the incident velocity for F−/0 projectiles during grazing (α = 1°) scattering from a LiF(001) surface. The data obtained for LiF(001) from Ref. [19]: F−, solid red squares; F0, solid violet circles. Theory: F−, dashed blue line, this model; F0, solid black line, Ref. [17]. The inset shows the electron-tunneling probability as a function of the projectile velocity for F−/LiF(001) based on Eq. ( |
Figure 
To obtain the detailed variation tendency for the F− ion fraction, we calculate dP(N = 30,v)/dv = 0, where

 | Fig. 4. dP(N = 30,v)/dv as a function of the negative projectile velocity v, where v0 = 0.056 a.u. represents the zero point of dP(N = 30,v)/dv. |
According to Eq. (
The Demkov model has been successfully applied to describe negative-ion fractions at the low-velocity threshold, whereas electron loss to an insulating surface via negative-ion scattering is not well understood. Because of the substantial difficulty associated with performing full quantum calculations to investigate this problem, the Landau–Zener model is introduced in this work to treat the formed quasi-molecular ionic and covalent diabatic potential curves crossing at a small distance for the electron loss at surface cations. This model presents an analytical formula and can explain the electron-loss process for negative ions during grazing scattering on an insulator LiF(001) surface in the velocity range v = 0–0.1 a.u. The calculated results are in good agreement with the only available experimental data. It should be emphasized that the derived model and conclusions based on this low-velocity range can be generalized, even though they are based on the results of a specific case, i.e., a F−–LiF(001) surface. We expect that this work will provide a fundamental basis for future detailed studies of electron loss during negative-ion surface scattering using both experimental and theoretical approaches.
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 | |
| 18 | |
| 19 | |
| 20 | |
| 21 | |
| 22 | |
| 23 | |
| 24 | |
| 25 | |
| 26 | |
| 27 | |
| 28 | |
| 29 | |
| 30 | |
| 31 | |
| 32 | |
| 33 | |
| 34 | |
| 35 | |
| 36 | |
| 37 | |
| 38 | |
| 39 | |
| 40 | |
| 41 | |
| 42 | |
| 43 | |
| 44 | |
| 45 | |
| 46 |




