Low-dimensional materials, especially one-dimensional (1D) nanoribbons, have attracted significant attention from the scientific community during the past two decades due to their interesting electronic properties associated with their low dimensionality and the resulting quantum confinement effect. In the past few years, graphene nanoribbons (GNRs), thin strips of graphene, have been extensively studied because of their rich and exotic physical properties which depend on their size and edge termination.^[1–3] First-principles calculations have revealed that GNRs with hydrogen saturated armchair- or zigzag-shaped edges always have a nonzero direct band gap which decreases as the ribbon width increases. The band gap variation for armchair GNRs (AGNRs) exhibits distinct “family behaviors”.^[4] The band gaps of AGNRs arise from both quantum confinement and the crucial effect of the edges, while for zigzag GNRs (ZGNRs), gaps appear because of a staggered sublattice potential on the hexagonal lattice due to edge magnetization.^[1,4–6] Besides GNRs, some other layer-structured nanoribbons, such as boron nitride nanoribbons (BNNRs) and MoS₂ nanoribbons, have also been studied intensively.^[7–9] It is found that the band gap of hydrogen-terminated zigzag BNNRs is indirect and decreases monotonically with the increasing ribbon width. However, direct band gap oscillation is observed for armchair BNNRs,^[10,11] which tends to converge to a constant value when the ribbon is wider than 3 nm. In contrast, zigzag edged MoS₂ nanoribbons show a metallic behavior irrespective of the ribbon width, while armchair edged ones are semiconducting and the band gaps converge to a constant value as the ribbon width increases.^[12]

As a wide indirect-band-gap semiconductor with uniform layered structure, gallium sulfide (GaS)^[13] has been used in photoelectric devices, electrical sensors, and nonlinear optical applications and gained renewed interest.^[14] In its bulk form, GaS usually crystallizes into a layered structure, S–Ga–Ga–S (Ga₂S₂), in which each layer consists of two AA-stacked hexagonal sublayers of Ga atoms sandwiched between two hexagonal sublayers of S atoms. These layers are bound in a three-dimensional (3D) structure by the nonbonding interaction through the S atoms along the vertical axis.^[14] Recently, the micromechanical cleavage technique (as originally used in peeling off graphene from graphite) was successfully used to fabricate single-layer sheets of Ga₂S₂.^[15,16] A theoretical calculation based on the density functional theory (DFT) has showed that the single-layer Ga₂S₂ nanosheet is dynamically stable and is a indirect-band-gap semiconductor with an unusual inverted sombrero dispersion of holes near the top of the valence band.^[17] As for the electronic properties of Ga₂S₂ nanoribbons (Ga₂S₂-NRs) which are important in realistic device applications, very few reports are available in the literature, to the best of our knowledge.

The purpose of this work is to investigate the electronic structures of Ga₂S₂-NRs by performing first-principles DFT calculations. The effects of different ribbon widths and different edge structures are studied. Furthermore, the relative stabilities of these nanoribbons are also investigated. In the next section, we describe our computational method. Section 3 presents our calculated results, and the last section is devoted to conclusions.

The models of Ga₂S₂-NRs are constructed by cutting out a stripe of single-layer Ga₂S₂ nanosheet with the desired edges and widths. Adopting a similar notation used to describe GNRs,^[1,2,18] we use the number of zigzag lines (N_z) or dimer lines (N_a) to present the width of a zigzag-edged ribbon (Ga₂S₂-ZNR) or a armchair-edged ribbon (Ga₂S₂-ANR) and denote the ribbon by N_z–Ga₂S₂-ZNR (as illustrated in Fig. 1(a)) or N_a–Ga₂S₂-ANR (as illustrated in the Fig. 1(b)).

Fig. 1.

	Figure Option ViewDownloadNew Window
	Fig. 1. Top and side views of the atomic structures of 6-Ga2S2-ZNR (a) and 11-Ga2S2-ANR (b). The ribbon width and 1D unit cell distance are denoted by Wz (Wa) and dz (da) for the ZNRs (ANRs), respectively. The ribbons are extended periodically along the x direction.

Calculations of structure optimization and band structure are carried out by using a first-principles pseudopotential plane wave method based on DFT, as implemented in the Vienna ab initio simulation package (VASP).^[19] The projector augmented wave method (PAW)^[20] is used to describe the ion-electron interaction. The electron exchange and correlation are treated by the generalized gradient approximation (GGA)^[21] in the version of Perdew–Burke–Ernzerhof (PBE).^[22] A kinetic energy cutoff of 600 eV is adopted for the plane-wave expansion of the wave function. The 4s²4p¹ electrons of Ga, and 3s²3p⁴ electrons of S are treated as valence electrons. Periodic boundary conditions (PBC) are employed for the infinitely long nanoribbon systems and a vacuum space of 10 Å in each direction perpendicular to the ribbon is used to eliminate the interaction between the periodic images. The atomic structures of the systems, including the lattice parameters and atomic positions, are fully relaxed by the conjugate gradient method until the residual forces acting on each atom are less than 0.001 eV/Å. For the structure optimization a Monkhorst–Packs k-mesh of 1 ×1×12 is used for the Brillouin zone (BZ) sampling. The band structures are presented by 45 k-points along the X axis in the BZ.

We first optimize the atomic structure of a periodic 2D Ga₂S₂ monolayer, in which Ga–S and Ga–Ga atoms are linked covalently in the quadruple layer. The optimized bond lengths of Ga–S and Ga–Ga are 2.37 Å and 2.47 Å, respectively. The Ga–S–Ga (or S–Ga–S) and Ga–Ga–S bond angles are 100.38° and 117.50°, respectively. The thickness of the quadruple layer is 4.76 Å. The computed binding energy is 3.64 eV per atom. The Ga₂S₂ monolayer is found to be a semiconductor with an indirect band gap of 2.38 eV on the DFT/PBE level. These results are in good agreement with recent DFT calculations.^[17,23] We note that Kohn–Sham DFT calculations usually underestimate band gaps of semiconductors because of the lacking of the derivative discontinuity in the energy functionals. A hybrid DFT calculation^[17] gives a larger value of the indirect band gap, 3.28 eV. Although the Kohn–Sham DFT has the band gap issue, it can usually give reasonable shapes of energy bands and wave functions in the vicinity of the Fermi level, compared to results from quasiparticle GW calculations.

We consider two different directions of termination for Ga₂S₂-NRs, zigzag and armchair, and for each direction of termination we consider the bare and H-saturated edge configurations. In order to investigate the width dependence of the electronic properties, we perform calculations for different ribbon widths, up to N_z = 24 and N_a = 19 (i.e., 24-Ga₂S₂-ZNR and 19-Ga₂S₂-ANR). Since qualitatively similar results are observed for the different widths, here we first take the 6-Ga₂S₂-ZNR with a width of 17.37 Å and 11-Ga₂S₂-ANR with a width of 18.37 Å as prototypes to present our results (see Fig. 1). After the structure optimization, the bond length between Ga and S atoms varies depending on their position in the ribbon. For the 6-Ga₂S₂-ZNR, the Ga-S bond lengths are 2.36 Å and 2.37 Å at inner sites, and 2.41 Å and 2.24 Å at the Ga-terminated and S-terminated edges, respectively. The bond angles of Ga–Ga–S and S–Ga–S at the inner sites are 117.43° and 100.24°, respectively. Because of the edge relaxation, the two angles change to 105.60° at the Ga-terminated edge and 108.48° at the S-terminated edge. In the case of the 11-Ga₂S₂-ANR, the edge S atoms tend to shift outward slightly. The Ga–S bond lengths are 2.36 Å, 2.37 Å, and 2.41 Å at the inner sites and 2.21 Å at the two edges. The Ga–Ga bond lengths are 2.48 Å, 2.47 Å, and 2.50 Å at the inner sites and 2.48 Å at the two edges. The bond angles of Ga–Ga–S and S–Ga–S are 117.50° and 100.36°, respectively, at the inner sites. These results show strong edge-induced atomic relaxation which results in quite different bond lengths and angles at the edges compared to those in 2D Ga₂S₂ monolayer. This behavior is quite different from the cases of GNRs and BNNRs where the edge distortion is much smaller.

Our calculations for the ZNRs show that their electronic structures are spin polarized. To carefully find out the spin configuration of the ground state, we perform total energy calculations for all possible spin configurations: Ferromagnetic (FM), nonmagnetic (NM), and various antiferromagnetic (AFM) configurations. As an example, the results for 6-Ga₂S₂-ZNR are summarized in Table 1S (see Supplementary Information). These results suggest that the FM configuration is the most stable one for both the bare and H-terminated systems.

The band structures of 6-Ga₂S₂-ZNR with bare and H-saturated edges are shown in Figs. 2(a) and 2(c) for the two spin components: up-spin (majority) and down-spin (minority), respectively. One can see that the band structures of 6-Ga₂S₂-ZNR exhibit a metallic nature: there are one or two bands crossing the Fermi level regardless of the H-passivation, which is similar to the behavior of MoS₂ nanoribbons.^[24,25] We find that this metallic nature holds for all Ga₂S₂-ZNRs studied (up to N_z = 24) regardless of the ribbon width. One should note that the difference between the up-spin and down-spin band structures exists only around the Fermi energy, indicating that the spin polarization originates from the states near the Fermi energy.

Fig. 2.

	Figure Option ViewDownloadNew Window
	Fig. 2. Calculated spin-polarized band structures (left: majority spin; right: minority spin) and corresponding local density of states (LDOS) near the Fermi level for bare 6-Ga2S2-ZNR [panels (a) and (b)] and H-terminated 6-Ga2S2-ZNR [panels (c) and (d)].

In order to understand the characteristics of these bands near the Fermi energy, we plot their local density of states (LDOS) in Figs. 2(b) and 2(d) for the bare and H-saturated ribbons, respectively. It can be seen that in both of the cases the local density of states is located around the edges, indicating that the metallic nature of Ga₂S₂-ZNRs is mainly due to the spin-polarized edge states. To further show the origin of these metallic bands, we also calculate the total density of states (TDOS) and projected density of states (PDOS) of 6-Ga₂S₂-ZNR (as shown in the following Fig. 3). The states around the Fermi level in both of the spin channels are dominated by the 4s and 4p states of the edge Ga atoms and 3p states of the edge S atoms. Further Mulliken population analyses show that the spin polarization is mainly due to the ferromagnetic (FM) state of the Ga-terminated edge regardless of the H-saturation.

Fig. 3.

	Figure Option ViewDownloadNew Window
	Fig. 3. Spin-dependent total and partial density of states for bare 6-Ga2S2-ZNR (a) and H-terminated 6-Ga2S2-ZNR (b).

In contrast, our calculations for the ANRs show that their electronic structures are spin unpolarized. Both the bare and H-saturated Ga₂S₂-ANRs exhibit a semiconducting nature. As an example shown in Fig. 4(a), bare 11-ZGa₂S₂-ANR is a typical semiconductor with an indirect band gap of 1.44 eV. In this case, the valence-band maximum (VBM) occurs along the Γ–K direction, and the conduction band minimum (CBM) lies at the K point. We note that the lowest conduction band and highest valence band are very flat, which is similar to the case of BNNRs.^[26] Generally, such a flat valence band is due to very localized electronic states and may induce a localized magnetic moment. To check this, we calculate the DOS and PDOS of the bare 11-Ga₂S₂-ANR (see Fig. 1S in Supplementary Information). The results show that the states around VBM and CBM are dominated by the 4s and 4p states of edge Ga atoms and 3p states of edge S atoms. This is consistent with the later LDOS analyses in Figs. 4(b) and 4(c). The null result of the atomic magnetic moments confirms that Ga₂S₂-ANRs are spin unpolarized semiconductors. When the edge Ga and S atoms are saturated by H atoms, Ga₂S₂-ANRs are still indirect band gap semiconductors but with a larger band gap (see Fig. 4(f)) and the VBM and CBM are now located at the Γ and K point, respectively.

Fig. 4.

	Figure Option ViewDownloadNew Window
	Fig. 4. Band structures and corresponding LDOS for CBM and VBM of the 11-Ga2S2-ANR. Panels (a), (b), and (c) correspond to the bare Ga2S2-ANR, panels (d), (e), and (f) correspond to the H-terminated Ga2S2-ANRs. Each LDOS figure contains a top view (left) and a side view (right) of the LDOS isosurface of the specified states at CBM or VBM. The Fermi level is set to be zero.

To analyze the characteristics of the VBM and CBM and the influence of the edges, we calculate the LDOS isosurfaces for the energies around the VBM and CBM of the bare and H-saturated 11-Ga₂S₂-ANR (see Figs. 4(b), 4(c), 4(d), and 4(e)). In the bare system the large edge relaxation (reconstruction) may weaken the dangling-bond states. However, the states of VBM and CBM are still mainly determined by the dangling-bond-related states which are driven from Ga-4p and S-3p orbitals. Therefore, their LDOS are mainly localized around the edges of the ribbon (see Figs. 4(b), 4(c)) and form flat bands.^[24] Moreover, because of this edge-state effect, the converged band gap (1.45 eV) (see the discussion later) of bare Ga₂S₂-ANRs becomes smaller than that of the 2D Ga₂S₂ monolayer (2.38 eV).

When the edge Ga and S atoms are saturated by H atoms, the dangling-bond edge states disappear and thus the band gap increases. As can be seen in Fig. 4(d), now the LDOS of the CBM are mainly located near the center of the ribbon. For the VBM, its LDOS are nearly uniformly distributed throughout the ribbon though very weak edge states remain (see Fig. 4(e)). In contrast with the bare systems, now the converged band gap (2.45 eV) (see the discussion later) of H-saturated Ga₂S₂-ANRs becomes slightly larger than that of the 2D Ga₂S₂ (2.38 eV).

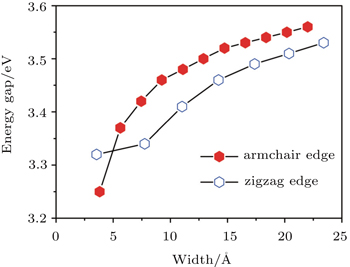
Next let us look at the variation of band gap as a function of ribbon width for both the bare and H-sturated ANRs. As shown in Fig. 5, all the Ga₂S₂-ANRs are semiconducting and their band gaps are sensitive to the structural symmetry and ribbon width. Generally, owing to the quantum confinement effect the band gap E_g should decrease with increasing ribbon width N_a. However, here the variation of E_g with N_a shows an oscillatory (or family) behavior, especially for the narrow ribbons (N_a < 8). Specifically, antisymmetric Ga₂S₂-ANRs (N_a = 2m, where m is an integer) have larger band gaps than the neighboring symmetric ones (N_a = 2m − 1). This ’family behavior’ was also observed previously in armchair-edged GNRs,^[4] BNNRs,^[26] and MoS₂ nanoribbons,^[12,27] where a width-dependent oscillation in band gap occurs. When the ribbon becomes wide enough (> 13 Å or N_a > 8), the band gaps tend to converge to a constant value (∼ 1.45 eV), being smaller than the bulk band gap of the 2D Ga₂S₂ monolayer (2.38 eV). To carefully confirm this tendency, we further do a calculation for 19-Ga₂S₂-ANRs (width 33 Å), which also shows a band gap of 1.45 eV. In the case of H-terminated ANRs (see Fig. 5), similar behavior is found although their band gaps converge to a larger value of 2.46 eV due to the diminishing edge states. The variation of the band gap with N_a may be an important advantage for their applications in nanotechnology because it may lead to the formation of quantum dot or multiple quantum wells through the width modulation.^[12,28]

Fig. 5.

	Figure Option ViewDownloadNew Window
	Fig. 5. Band gaps of a series of bare Ga2S2-ANRs (3 ≤ Na ≤ 13) as a function of the ribbon widths (filled red lozenges). For a comparison, the result for the corresponding hydrogen saturated Ga2S2-ANRs is also shown (voided blue lozenges).

Fig. 6.

	Figure Option ViewDownloadNew Window
	Fig. 6. Binding energy of bare Ga2S2-ZNRs (3 ≤ Nz ≤ 8) and Ga2S2-ANRs (6 ≤ Na ≤ 13) as a function of the ribbon width.

Finally, we would like to discuss the stability of Ga₂S₂-NRs, which is quite important because it determines whether this nanostructure can be realized experimentally. The stabilities of different nanoribbons and nanoclusters can be evaluated with their binding energies; those with larger binding energies would be more stable. To estimate the stability, we calculate the binding energy per atom as a function of the ribbon width for bare Ga₂S₂-NRs in the following way:^[12] E_b = (nE_Ga + mE_S − E_GanSm)/(n + m), where E_Ga, E_S, and E_GanS_m are the total energies of Ga, S atoms, and Ga_nS_m, respectively, with n and m being the number of Ga and S atoms, respectively. As is shown in Fig. 6, the binding energy increases monotonically with increasing ribbon width for both zigzag and armchair Ga₂S₂-NRs. The binding energies of the armchair ribbons are slightly higher than those of the zigzag ribbons with comparable widths, indicating that armchair Ga₂S₂-NRs are more stable than zigzag ones. It is important to note that although the binding energy of the nanoribbons (except for N_a = 3) is smaller than the 2D Ga₂S₂ monolayer, it is larger than that of Ga₂S₂ nanoclusters with stable configurations.^[29] Therefore, it is reasonable to expect that stable bare Ga₂S₂-NRs are possible to make experimentally in the future. Since dangling bonds are saturated by H atoms in H-saturated Ga₂S₂-NRs, their stability should be even better.

In summary, by performing first-principles DFT calculations we have investigated systematically the electronic properties of Ga₂S₂ nanoribbons which have not been realized yet but the corresponding 2D monolayer has been successfully fabricated experimentally. We have considered the bare and H-saturated zigzag- and armchair-edged nanoribbons with different ribbon widths (up to 3 nm). It is found that the electronic properties of the nanoribbons strongly depend on their edge structures. The Ga₂S₂-ZNRs display an intrinsic metallic character with FM coupling, raised from Ga-4p and S-3p states at the Ga-terminated edge while the Ga₂S₂-ANRs are indirect-band-gap semiconductors without spin polarization. The band gap of bare Ga₂S₂-ANRs exhibits an oscillation behavior with increasing ribbon width and ultimately converges to a constant value of 1.45 eV when the ribbon becomes wide enough (>13 Å). The H-saturated Ga₂S₂-ANRs have the similar behavior but with larger converged band gap of 2.46 eV due to the saturation of the dangling bonds at the edges. Finally, we have studied the relative stabilities of the bare ZNRs and ANRs by calculating their binding energy per atom, and found that the ANRs are more stable than the ZNRs with a similar width. The binding energies are found to be slightly smaller than that of the 2D monolayer, but is larger than that of Ga₂S₂ nanoclusters with stable configurations, indicating that the bare ribbons can be expected to be realized experimentally in the future.