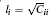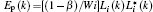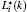† Corresponding author. E-mail:
‡ Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant Nos. 51276046 and 51506037), the Foundation for Innovative Research Groups of the National Natural Science Foundation of China (Grant No. 51421063), the China Postdoctoral Science Foundation (Grant No. 2016M591526), the Heilongjiang Postdoctoral Fund, China (Grant No. LBH-Z15063), and the China Postdoctoral International Exchange Program.
Direct numerical simulations (DNSs) of purely elastic turbulence in rectilinear shear flows in a three-dimensional (3D) parallel plate channel were carried out, by which numerical databases were established. Based on the numerical databases, the present paper analyzed the structural and statistical characteristics of the elastic turbulence including flow patterns, the wall effect on the turbulent kinetic energy spectrum, and the local relationship between the flow motion and the microstructures’ behavior. Moreover, to address the underlying physical mechanism of elastic turbulence, its generation was presented in terms of the global energy budget. The results showed that the flow structures in elastic turbulence were 3D with spatial scales on the order of the geometrical characteristic length, and vortex tubes were more likely to be embedded in the regions where the polymers were strongly stretched. In addition, the patterns of microstructures’ elongation behave like a filament. From the results of the turbulent kinetic energy budget, it was found that the continuous energy releasing from the polymers into the main flow was the main source of the generation and maintenance of the elastic turbulent status.
The rheological properties of the Newtonian fluid could be significantly modified by the addition of a small amount of flexible microstructures such as polymers or some surfactant additives, and the fluid turns to a viscoelastic one. Compared with the Newtonian fluid flow, two kinds of nonlinearity exist in viscoelastic fluid flow, which are nonlinear inertial and nonlinear elastic effects, but do not necessarily coexist.[1] As a result, a variety of different flow regimes turn up due to the additional elastic nonlinearity, depending on the feedback of microstructures on the main flow. The feedback is actually decided by microstructure status such as in a coiled or stretched configuration. For viscoelastic fluid flow, besides the well-known Reynolds number Re, the Weissenberg number Wi is another important dimensionless parameter and describes the competition between polymer stretching by main flow and microstructure relaxation by itself. For cases with Wi≪1, microstructures relax much faster than the main flow stretching, and thus they are always in a coiled state and embedded passively in the flow. In these cases, the feedback of microstructures on the flow could be ignored. However, for cases with Wi on the order of unity or larger, the striking feedback will be induced because of the significant growth of microstructure length. For example, the substantial reduction of turbulent drag resistance occurs in the inertial turbulent flow when inertial and elastic nonlinearity coexist[2] and has attracted numerous researchers.[3–7] On the other hand, at an arbitrarily low Reynolds number, with solely elastic nonlinearity the flow instability and even turbulent-like regime, i.e., elastic turbulence, are still possible to occur in the limit of large enough Wi, under which Newtonian fluid flow is definitely in the laminar regime.[8–10] The occurrence of flow instability or turbulence without nonlinear inertia implies great potential in enhancing heat and mass transfer efficiency in the micro-scale areas,[11–15] as well as special functional design in microfluidics.[16,17]
The present paper focuses on the elastic turbulence where the elastic nonlinearity dominates. It has been over ten years since the first report on elastic turbulence by Groisman and Steinberg.[9] So far, numerous researches on this phenomenon have been carried out to obtain insight into its underlying mechanism as well as to realize its application. From the experimental viewpoint, most of the early work was limited to the geometry with local curvature such as the swirling flow between two parallel disks, Taylor–Couette flows between two coaxial cylinders, as well as micro-scale flows in the curvilinear micro-channels.[18,19] Therein, the elastic turbulence was described as the flow regime after elastic instability, with significant growth of drag resistance, a wide range of energy spectrum, and fluctuating vortex structures random in time but smooth in space, and so on. However, for a long time, the curvature of the geometrical configuration was considered to be indispensable for the flow transition from laminar to purely elastic instability according to the linear stability analysis.[20,21] In these cases, the existence of curvature induces “hoop stress”, which is defined as the ratio of the local first normal stress difference and local curvature, and is responsible for the flow transition. McKinley[21] summarized the results in different geometries and put forward the critical condition for purely elastic instability: λUN1/(RΣ) ≥ M, where M is a constant and related with the geometry, R is the streamline curvature, N1 is the first normal stress difference, and Σ is the shear stress. In this condition, purely elastic instability and further elastic turbulence are considered to be impossible in a straight pipe or a parallel plate channel, since therein R is infinite, and the microstructures will be degraded before satisfying the above condition. However, the nonexistence of a linear transition does not guarantee the flow is absolutely stable, since only infinitesimal perturbations are taken into account in linear stability analysis. Actually, the finite perturbation usually exists in the real flow, where linear stability analysis loses its validity. The recent nonlinear stability analysis pointed out that the nonlinear transition is possible for inertialess viscoelastic flow.[22–24] It was then confirmed experimentally by Bonn[25] in a straight pipe and Pan[26] in a straight channel, where large fluctuations were firstly excited before entering measuring sections. In this straight pipe, it was found that the power law exponent of the energy spectrum is around −1.5, whereas it is between −3 and −4 in the curved geometry.[25]
As mentioned above, the elastic turbulence is induced by elastic nonlinearity. Therefore, knowledge of the microstructure characteristics is of primary importance to understand its underlying physical mechanism. Chu’s group has carried out a series of experimental measurements of single polymer behaviors in elongational and shear flows,[27,28] where the coil-stretch transition of single polymer was reported. It has now been argued that the occurrence of microstructure coil-stretch transition is a prior for elastic turbulence.[29–31] Nevertheless, with the current experimental technique, it is quite difficult to directly measure microstructure behaviors or its role in the elastic turbulence except through indirect estimation such as the Lyapunov exponent or total drag resistance.[31–33] This strongly limits our understanding of the whole process of elastic turbulence from the experimental viewpoint. In this sense, direct numerical simulation has been proven to be a complement to the experimental approach for any turbulent flow for many years. Through directly solving the governing equations of viscoelastic flow, the detailed information including not only flow field but also microstructure conformation field could be achieved, which is so far impossible for experimental approaches. In fact, several numerical simulations have been carried out on elastic turbulence, such as the Taylor–Couette flow,[35,36] the Kolmogorov flow,[37–39] and the Stokesian flow,[40] the flow in a three-dimensional (3D) curvilinear channel,[41] and straight channel[42] of viscoelastic fluids, based on which our knowledge of elastic turbulence has been greatly enriched. Therein, similar characteristics to those in experiments were reproduced such as the significant increase of drag resistance, faster spectrum decay, and so forth. Moreover, except geometries with local curvature DNSs[37,39,42] have already been reported and confirmed before the experimental proof in Refs. [25] and [26] that the elastic instability and turbulence are possible to be excited even with only rectilinear streamline flow.
In spite of its great fascination to researchers and the extensive range of potential applications, the understating of the elastic turbulence is still quite limited by now, especially the elastic turbulence in the rectilinear shear flow. Following our previous work, the current work further discusses the characteristics of elastic turbulence including statistical properties and structural properties, as well as its maintenance from the viewpoint of the global energy budget. The paper is organized as follows: Section 2 introduces the numerical models and governing equations used in the following sections; the numerical results are then discussed in detail in Section 3; Section 4 draws the conclusion of the present paper.
Direct numerical simulations (DNSs) of the viscoelastic fluid flow were carried out in a 3D parallel plate channel as illustrated in Fig.

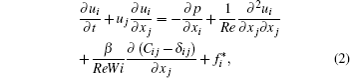



As for the spatial discretization, a second-order central difference scheme is used for the momentum transport equation, while the MINMOD scheme is used for the convective term in the Giesekus constitutive equation. The Adams–Bashforth scheme is used for time advancing to keep a second-order accuracy in time. As for the boundary condition, periodic conditions are adopted for both streamwise and spanwise directions, and the non-slip boundary condition for the top and bottom walls. Moreover, Re is set to be 1 for all cases and the channel flow of Newtonian fluid is definitely laminar. The simulations are conducted in a mesh with 64 × 64 × 64 grids, which has been verified to be fine enough for capturing all information desired for a very-low-Re elastic turbulence and is suitable for the computing resource in Ref. [42]. The further details on the numerical procedures could be found in Refs. [42] and [43].
For the convenience of later analysis, some basic variables are defined as follows. Based on the instantaneous velocity fields and polymer conformation, the global kinetic energy EK, elastic energy Ep, the enstrophy W, and strain S are defined as follows:
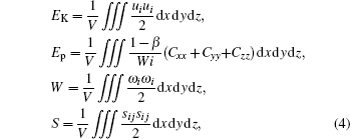
For the turbulent cases, the instantaneous velocity ui and polymer conformation field Ci j can be divided into the mean flow and the fluctuations i.e., 
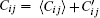


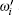
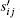
To obtain further insight into this intriguing phenomenon, this section analyzes the numerical results focusing on the structural and statistical characteristics, the generation and maintenance of the elastic turbulence following our previous study.[42] In our previous work, the critical criterion for the onset of elastic instability has been determined to be Wic > 5 under the same type of additional force. The following analysis is carried out mainly on the basis of the numerical databases, which have been proved to be above the onset of elastic instability in Ref. [42].
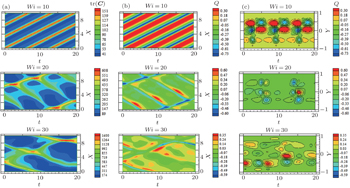
We start our analysis on flow structures by considering the pattern of velocity field (
To have an intuitive impression of the flow structures in the viscoelastic fluid flow above elastic instability, firstly the snapshots of the velocity field
 | Fig. 2. Snapshots of different fields in the x–y section z* = Sz/2 at the same time at Wi = 30: (a) u; (b) v; (c) tr( |
In Refs. [37], [38], and [40], the elastic turbulence was numerically investigated in a 2D rectilinear shear flow and has reproduced some basic phenomenology observed in the experiments. However, for every turbulent flow, it should be definitely 3D. To improve our understanding on 3D properties of elastic turbulence, figures
Moreover, the flow structures above elastic instability were also observed to be propagating along the streamwise with time in the form of elastic waves in the flow as reported in Ref. [38], which may be due to the non-homogeneous distribution of turbulent kinetic energy and polymer elastic potential energy. Figure
 | Fig. 3. Snapshots of flow motion (velocity component u) in the streamwise–spanwise (x–z) section y* = 0 (with strong velocity gradient): (a) Wi = 10; (b) Wi = 20; (c) Wi = 30. |
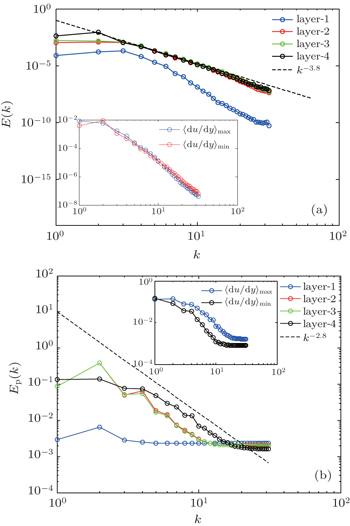
In the present paper, the flow was divided into 4 layers according to additional force, so it is possible to study the straight wall effect on elastic turbulence by comparing flow characteristics in different layers. Before this comparison, we firstly compare the flow motion especially the turbulent statistics near the wall in this channel with that in the curvilinear channel, which could be found in our previous numerical results obtained in a curvilinear channel[41] and this straight channel.[42] Similar to that in inertial turbulence and experimental observation in the curved geometry, two peaks of the velocity fluctuations could be observed near the wall for the curvilinear channel. However, in the current case, no peak of the velocity fluctuations is formed in layer-1, which is directly affected by the wall, indicating the straight wall may suppress the turbulent motion. In order to further confirm this, the attentions are then paid to the distributions of the microstructures extension and vortex structures as shown in Figs.
It then becomes natural to ask why the straight wall suppresses the elastic instability and turbulence and then why it could survive in the current simulation even with a straight wall. The “hoop stress” theory is used here to answer the above question. According to our numerical study, even without the geometry curvature the viscoelastic fluid flow could still be elastically turbulent. It is conjectured that the key of elastic turbulence occurrence does not lie in the geometrical curvature but the streamline curvature. In the curvilinear channel, the geometry provides the curved streamline which generates the “hoop stress”. The “hoop stress” then leads to the normal flow motion and amplifies the initial perturbations. In the current geometry, in the bulk flow region, the initial perturbations bring in the curved streamline by which the “hoop stress” could be generated and then maintain the elastic turbulence. Next to the wall, the flat-straight wall straightens the initial curved streamline, and then eliminates the “hoop stress”. Therefore, the flow therein tends to be more stable. The straight wall suppression effect may not only exist in the low-Re flows but also high-Re flows. However, the affecting region is related with Re. For the large-Re flows such as inertial turbulent flows, its effect is mainly confined in a very thin layer next to the wall, or within the thickness of the viscous sub-layer. Unlike large-Re flows, in the elastic turbulent flow with an extremely low Re, the straight wall effect will dominate the whole area if without any additional treatment. Then if the straight wall suppresses the elastic turbulent motion, why and how could it survive in the center? To answer this, the form of our external force and the role of layer-1 are considered. The existence of layer-1 (or the stable layer next to the wall) may block the straight wall effect from transferring into the center region. In this way the curved streamlines could be kept there far from the near wall region. In other words, this stable or blocking layer is of importance to the generation and maintenance of elastic turbulence in the channel without curvature. This conjecture still needs future experimental and numerical verifications.
Moreover, as shown in the inside inset of Fig.
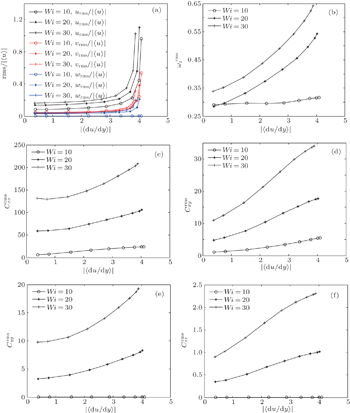
In this section, the statistical relationship between the microstructure behavior and the flow motion (turbulent characteristics) is investigated for the cases above elastic instability. As mentioned above, elastic turbulence is originated from the elastic nonlinearity of the viscoelastic fluid, which is closely related with the velocity gradient ∇
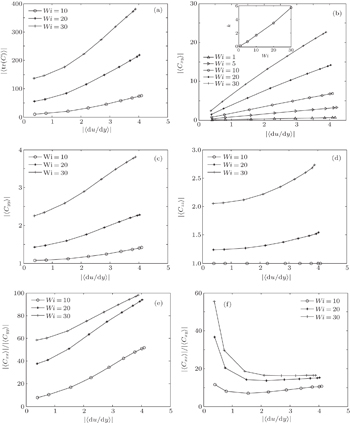 | Fig. 7. Averaged local velocity gradient |〈du/dy〉| at different Wi: (a) |〈tr(C)〉|; (b) |〈Cxy〉|; (c) |〈Cyy〉|; (d) |〈Czz〉|; (e) |〈Cxx〉|/|〈Cyy〉|; (f) |〈Cxx〉|/|〈Cxy〉|. |
In the inertial turbulence, the turbulent fluctuations and the vortex structures are generated and maintained through the Reynolds stress 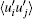
Before showing the numerical results, the energy budget for viscoelastic fluid flow was firstly derived. According to Eqs. (

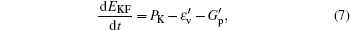
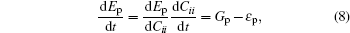
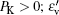
Firstly, the evolutions of EK, Ep, and EKF are shown in Fig. 
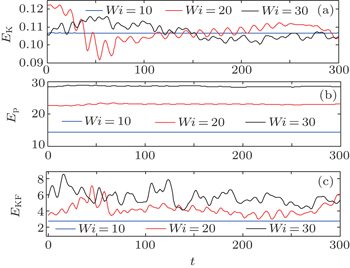 | Fig. 9. Temporal evolution of the global quantities including EK (a), Ep (b) and EKF (c) at different Wi. |
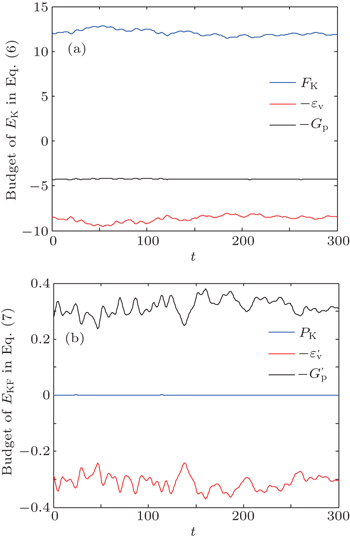 | Fig. 10. Temporal evolution of kinetic energy budget at Wi = 30: (a) EK based on Eq. ( |
In order to further understand this process, the instantaneous and fluctuating elastic effect Gp and 
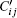
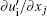

Finally, the generation and maintenance of vortex structures are discussed. In inertial turbulence, relative to the velocity fields, the velocity gradient contains more significant fluid mechanical information and its dynamical behavior is closely related with the mechanism of vortex stretching and the energy cascade.[45] Therefore, it is of primary importance to investigate the generation of the velocity gradient in a turbulent flow to understand its kinematics and dynamics. As mentioned before, the characteristics of elastic turbulence are quite different from those of inertial turbulence, such as vortex structures comparable with the scale of the flow geometry and faster decay of the turbulent kinetic energy.[9] These differences may lie in the generation of velocity gradient, which is the focus of this part: investigating the energy budget of global enstrophy (indicating the strength of rotating motion in the flow) and strain (indicating the strength of deforming motion in the flow) as well as the microstructure effect therein.
The global budgets of enstrophy and strain from the instantaneous and fluctuating viewpoints are as follows:




Temporal evolution of the enstrophy and strain from instantaneous and fluctuating viewpoints at different Wi. (a) W, (b) WF, (c) S, (d) SF.
Temporal evolution of budget for (a) W based on Eq. (
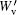

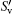
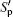
Figure 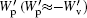
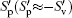

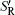
So far, the elastic turbulence is still poorly understood, due to the limitation of experimental techniques and the lack of numerical data, therefore our main goal is to obtain further insight to improve our knowledge of this intriguing phenomenon. DNSs of purely elastic turbulence in a 3D straight channel were carried out. Though the simulated geometry is very simple, most of the qualitative similar experimental observations have been reproduced in the current simulation. Following our previous research, the detailed characteristics of the elastic turbulence including the flow patterns and the role of velocity gradient, and the generation and maintenance from the energetic view point were presented in this paper. It is observed that in the elastic turbulence, the flow shows three dimensional characteristics with larger spatial scales, and the polymer elongation shows filament structures. The vortex tubes were found to be embedded in the regions where the polymers are strongly stretched. Besides, the straight wall effect on the characteristics was also investigated based on the kinetic energy and elastic energy spectrum, which indicates that the turbulent flow near the straight wall decays much faster, i.e., the straight wall tends to stabilize the turbulent flow. On the other hand, the existence of layer-1 in the simulation localizes this effect, which helps the fluctuations in the outer layers to survive from the straight wall effect. Moreover, in the elastic turbulent flow, the velocity gradient plays a dominant role in the flow characteristics, for example, the turbulent intensity is found to increase with that of the velocity gradient. As for the generation and maintenance of elastic turbulence, from the energetic viewpoint, it is found apparently from the instantaneous viewpoint that the additional force counteracts the viscous dissipation and elastic absorption, and the polymers absorb energy from the main flow. However, different from the inertial turbulence, there is continuous energy released from the polymers into the flow, which counteracts the viscous dissipation and sustains the turbulent status from the fluctuating viewpoint. Therefore, in elastic turbulence, we reach a conclusion that it is the fact that enough energy is released from the polymers which generates and maintains the elastic turbulence.
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 | |
| 18 | |
| 19 | |
| 20 | |
| 21 | |
| 22 | |
| 23 | |
| 24 | |
| 25 | |
| 26 | |
| 27 | |
| 28 | |
| 29 | |
| 30 | |
| 31 | |
| 32 | |
| 33 | |
| 34 | |
| 35 | |
| 36 | |
| 37 | |
| 38 | |
| 39 | |
| 40 | |
| 41 | |
| 42 | |
| 43 | |
| 44 | |
| 45 |