In the past few years we have seen the explosive growth of the non-volatile semiconductor memory market because of the unceasing demand for higher memory density and lower bit cost.^[1] During the aggressive scaling of flash memory technology, the floating gate structure has faced great challenges from both technological and physical limitations, such as reducing coupling ratio, cell-to-cell interference, and increasing gate leakage current.^[2] In order to continue the scaling trend, great effort has been devoted to developing next-generation memory structures.^[3–6] Among these structures, the charge trapping memory (CTM) shows the most excellent potential as one of the most promising candidates for future memory solutions.^[7–9] Furthermore, in recent years, high-density CTM in three-dimensional (3D) architectures for the NAND applications has drawn a great deal of attention.^[10–12]

Under this circumstance, understanding the physical mechanisms in CTM has growing importance in terms of designing and optimizing CTM devices. The trap-assisted tunneling (TAT) is one of the most important mechanisms influencing the memory performance. On the one hand, TAT is an indispensable part of the tunneling current due to the existence of intrinsic defects in oxide layers. An accurate calculation of TAT current is crucial for achieving high accuracy in modeling CTM performance. On the other hand, it is largely accepted that electrical stress in the tunneling oxide during program/erase (P/E) cycle leads to the generation of interface defects and bulk traps in oxide layers.^[13,14] In this regard, the TAT mechanism is related to reliability issues of the memory cells after P/E cycle, leading to a variation of memory characteristics. Especially, degradation in tunneling oxide can cause the increase in charge loss during retention operation. However, previous studies on modeling the TAT mechanism mainly focused on the gate leakage current of the MOS structure.^[15–17] Only little work has addressed the TAT effect in the context of flash memory cells.^[18,19]

In this paper, the TAT mechanism in CTM cells is carefully modeled and implemented in the developed simulator^[20–22] for NAND flash memory. The influence of the TAT mechanism on CTM performance is investigated in consideration of various oxide trap positions and energy levels. The programming and retention performances of CTM after P/E cycle are also evaluated.

The device structure we used to evaluate the influence of TAT on CTM performance is a standard CTM cell with 4.5-nm/6-nm/10-nm (SiO₂/Si₃N₄/Al₂O₃) gate stacks as shown in Fig. 1.

Fig. 1.

	Figure Option ViewDownloadNew Window
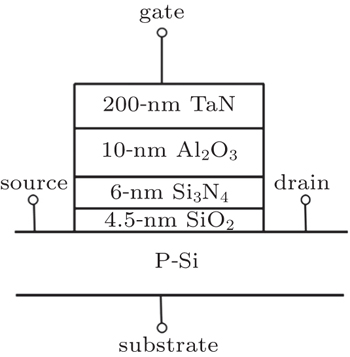	Fig. 1. Schematic illustration of the simulated standard CTM cell with a 4.5/6/10 nm (SiO2/Si3N4/Al2O3) gate stack.

The TAT mechanism is modeled as a two-step process,^[23] i.e., the electron capture and emission of the oxide traps. The TAT current driven through each oxide trap is given by the capture and emission times for each trap, τ_c,ch/csl and τ_e/csl respectively, considered from the charge reservoir, i.e., channel or charge storage layer as schematically illustrated in Fig. 2.

Fig. 2.

	Figure Option ViewDownloadNew Window
	Fig. 2. Schematics of the capture and emission time constants for calculating TAT current in (a) programming and (b) retention operations.

Accumulating the current-density contributions from the traps in a small interval dx at each distance x, the total TAT current density through the entire oxide layer is expressed as

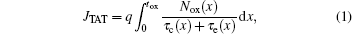
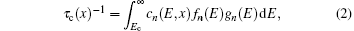
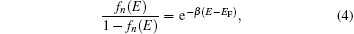
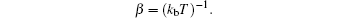
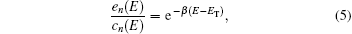
It should be mentioned that the calculations of capture and emission coefficients are related to the energetic position of E_T with respect to the energy level E in the integration. When E_T is lower than E, the capture coefficient is energy-independent and can be written as

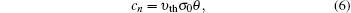
In order to improve calculation efficiency, an approximation is made to solve the above complicated integral by assuming E = E_c for calculating the time constants.^[24] Overall, using Eqs. (1)–(6), we can rewrite the capture and emission time constants as follows:

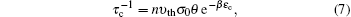
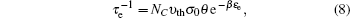
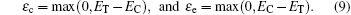
The abovementioned physical model accounting for the TAT mechanism has been incorporated into our calibrated two-dimensional (2D) self-consistent CTM simulator,^[21] which carefully takes into consideration the DT/FN tunneling process, charge trapped/de-trapping mechanisms, and drift-diffusion transport in the gate stack of memory cells. In addition, oxide traps with arbitrary energy level and spatial distribution are considered in the simulation. The main parameters adopted in the simulation are summarized in Table 1.^[26,27]

Table 1.

Table 1.

Table 1. Main parameters for the simulation. . Parameter Symbol Value SiO2 effective mass mox 0.42m0 SiO2 trap cross-section σn 5 × 10−14 cm2 SiO2 trap energy ET 2.0 eV Si3N4 effective mass mSiN 0.5m0 Si3N4 trap energy ET,SiN 1.5 eV

Table 1. Main parameters for the simulation. .

In order to obtain an overview of the influences of the TAT mechanism on programming and retention characteristics of CTM cells, we first perform the simulations in the cases with and without considering the TAT effect. In addition to the TAT mechanism, in the simulation the direct and FN tunneling process within the tunneling oxide are taken into consideration. Comparisons between simulation prediction and experimental measurement are also made. Figure 3 shows a good reproduction of experimental data^[27] for all programming voltages considered. A uniform spatial distribution of traps is assumed for the charge storage layer, under a trap density of N_t = 7 × 10¹⁹ cm^{− 3} and a trap cross section σ_n = 1 × 10^{− 14} cm². The trap density is an important factor in determining the memory window,^[28] and hence is obtained from fitting the experimental characteristics. For the simulation of TAT contribution, we consider typical parameters for oxide defects in accordance with those reported previously^[29] for thermally grown oxides. The intrinsic trap distribution across the tunneling oxide is assumed to be uniform under an oxide defect density of N_ox = 3 × 10¹⁶ cm^{− 3}, a trap energy level around 2 eV, and a trap cross section of σ_T = 8 × 10^{− 14} cm². For the simulated memory cell, the interface traps located at tunneling oxide borders are not included in the simulation. It can be seen that without considering the TAT current, the programming speed is underestimated and simulations and measurements are not in agreement with each other. In addition, the role played by TAT current is found to be non-negligible at lower oxide fields: lower programming voltages, and larger occupation of the traps in the charge storage layer (longer programming time). Using the same material parameters for the charge storage layer and slightly modified parameters for intrinsic oxide defects (N_ox = 2 × 10¹⁶ cm^{− 3} and σ_T = 5 × 10^{− 14} cm²), good agreement between experimental retention measurements^[30] and simulations under a wide variety of temperatures can be achieved as shown in Fig. 4. The result indicates that modeling the TAT mechanism is also crucial in predicting retention characteristics, which can lead to extra charge loss from the charge storage layer.

Fig. 3.

	Figure Option ViewDownloadNew Window
	Fig. 3. Comparison between experimental programming data and simulation results of CTM cells and influence of TAT on programming characteristics.

Fig. 4.

	Figure Option ViewDownloadNew Window
	Fig. 4. Comparison between experimental retention and simulation predictions of CTM cells under different temperatures and influence of TAT on retention characteristics.

The defect traps allow an extra tunneling path in the oxides, but not all traps have equivalent contribution to TAT current. From Eq. (1), it is known that capture and emission time constants are used to calculate TAT current density of each oxide trap. Figure 5 shows the variations of capture and emission time constants and normalized TAT current contributions with position along tunneling oxide under 16-V programming voltage at 1 μs for the simulated device. It is found that only the oxide traps in a small distance (approximately 1 nm) at the position of 3.5 nm from the substrate interface make the main contribution to the overall TAT current. Similarly, figure 6 shows the variations of capture and emission time constants and normalized TAT contribution with position along tunneling oxide for 375 K retention simulation at 10⁷ s. Oxide traps located within a length of 0.2 nm at the position of 3 nm from the substrate interface are related to major TAT current.

Fig. 5.

	Figure Option ViewDownloadNew Window
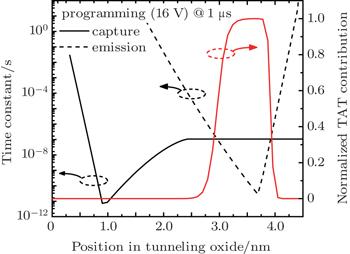	Fig. 5. Capture and emission time constants used to calculate TAT current density along tunneling oxide and the related normalized TAT current contribution under 16-V programming voltage at 1 μs.

Fig. 6.

	Figure Option ViewDownloadNew Window
	Fig. 6. Capture and emission time constants used to calculate TAT current density along tunneling oxide and the related normalized TAT current contribution for 375-K retention simulation at 107 s.

However, the positions of peak contribution to the overall TAT current are variable with time evolution under programming and retention operations as shown in Fig. 7. In the programming process, the shape of the curve for normalized TAT contribution becomes narrower with time evolution. Simultaneously, the position of the maximum contribution shifts towards the substrate interface. In comparison, the shape of the curve keeps unchanged with the peak shifting towards the charge storage layer interface during retention. The variation in positions of the maximum contribution can be ascribed to the movement of band edge in different phases of the programming and retention operations.

Fig. 7.

	Figure Option ViewDownloadNew Window
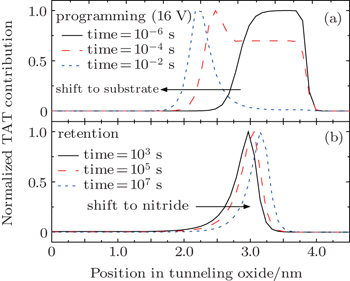	Fig. 7. The variations of normalized TAT contribution with position in tunneling oxide with time evolution in (a) programming and (b) retention operations.

Apart from the position of oxide defects, trap energy level is another major factor to determine TAT current. To investigate the influences of the trap energy level and spatial position on TAT current density, we assume that the trap distribution in tunneling oxide has a Gaussian distribution with a peak value of 7 × 10¹⁸ cm^{− 3} and a small standard deviation of 0.2 nm. Simulations of devices with various peak positions and trap energy levels are performed. Figure 8 shows the TAT current density under 16-V programming voltage at 1 μs of a device with a 4.5/6/10 nm gate stack (SiO₂/Si₃N₄/Al₂O₃). The oxide traps located around 1 nm from the oxide/nitride interface with lower energy level are related to larger TAT current density. Figure 9 shows the TAT current densities of devices with various peak oxide trap positions and energy levels at 10⁷ s of retention under 360 K temperature. It is shown that oxide traps located at 1.4 nm from the oxide/nitride interface are related to the maximum TAT current density, which has little dependence on the trap energy level ranging from 0.6 eV to 4.0 eV.

Fig. 8.

	Figure Option ViewDownloadNew Window
	Fig. 8. TAT current densities under 16-V programming voltage at 1 μs of devices with various peak positions and trap energy levels.

Fig. 9.

	Figure Option ViewDownloadNew Window
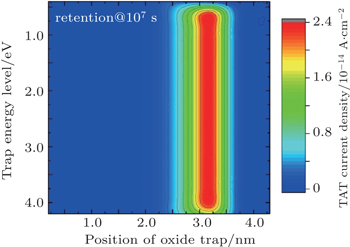	Fig. 9. TAT current densities at 107 s of retention operation under 360-K temperature of devices with various peak positions and trap energy levels.

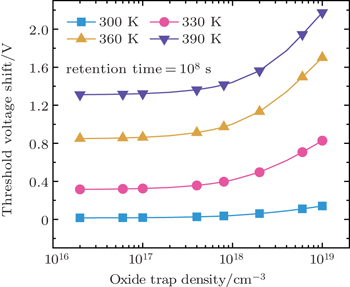
During P/E operations, the electric field in tunneling oxide can typically exceed 10 MV/cm.^[31] A Large number of P/E cycles leads to the generation of oxide traps and thus causes reliability issues of CTM cells. The influences of TAT on programming and retention operations are strongly correlated with trap density in tunneling oxide. Figure 10 shows the programming speeds under different programming voltages with increasing the level of tunneling oxide degradation. A unanimous programming window of 5 V is used for all cases. It can be seen that programming under lower voltage is more sensitive to oxide degradation. Figure 11 shows the threshold voltage shift after 10⁸ s under various retention temperatures with increasing the level of tunneling oxide degradation. Higher temperature is found to be more sensitive to oxide degradation.

Fig. 10.

	Figure Option ViewDownloadNew Window
	Fig. 10. Programming speeds under different programming voltages with increasing the level of tunneling oxide degradation.

Fig. 11.

	Figure Option ViewDownloadNew Window
	Fig. 11. Threshold voltage shifts after 108 s under various retention temperatures with increasing the levels of tunneling oxide degradation.

In this paper, we carefully model TAT mechanism in CTM cells and evaluate the influences of TAT on programming and retention characteristics. Our results indicate that the TAT mechanism is a critical factor for CTM operations, especially at low tunneling oxide fields. The influence of the TAT mechanism on CTM performance is investigated in consideration of various trap positions and energy levels in the tunneling oxide.

The results show that only the oxide traps at a small distance are related to a major contribution to TAT current. In addition, the positions corresponding to the maximum contribution shift towards the substrate interface and the charge storage layer interface during programming and retention operations, respectively. Lower programming voltage and retention operations under higher temperature are more sensitive to tunneling oxide degradation.