† Corresponding author. E-mail:
‡ Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant Nos. 11174058 and 61376093), the Fund from Shanghai Municipal Science and Technology Commission (Grant No. 13QA1400400), the National Science and Technology Major Project, China (Grant No. 2011ZX02707), and the Innovation Program of Shanghai Municipal Education Commission (Grant No. 12ZZ010).
Two-dimensional atomic-layered material is a recent research focus, and single layer Ta2O5 used as gate dielectric in field-effect transistors is obtained via assemblies of Ta2O5 nanosheets. However, the electrical performance is seriously affected by electronic defects existing in Ta2O5. Therefore, spectroscopic ellipsometry is used to calculate the transition energies and corresponding probabilities for two different charged oxygen vacancies, whose existence is revealed by x-ray photoelectron spectroscopy analysis. Spectroscopic ellipsometry fitting also calculates the thickness of single layer Ta2O5, exhibiting good agreement with atomic force microscopy measurement. Nondestructive and noncontact spectroscopic ellipsometry is appropriate for detecting the electrical defects level of single layer Ta2O5.
In pursuit of a faster response speed and lower power consumption in field effect transistors, the channel length becomes smaller and smaller, and so does the thickness of gate dielectric.[1] Two-dimensional atomic-layered channel materials such as monolayer MoS2[2] have attracted a great deal of attention recently, and the FETs fabricated with them exhibit high carrier mobility and excellent on/off current ratio.[3] However, wide application is impossible without the same atomic-layered dielectrics, which have rarely been reported. Here, we investigate the single layer two-dimensional Ta2O5 that can function as a gate dielectric.[4] Compared with conventional SiO2, on which the carrier mobility is limited by scattering from surface optical phonons or charged surface states and impurities,[5] Ta2O5 has many superior properties including a high dielectric constant,[4] large refractive index value,[6] as well as high chemical and thermal stability,[7] etc.
Single layer Ta2O5 can be obtained via assembling Ta2O5 nanosheets, i.e., the so-called sequential adsorption method.[8–10] Nanosheets have an ultrathin thickness of 0.5 nm–3 nm and a lateral size of micrometers range, meaning that they are composed entirely of surface atoms and thus can be regarded as a unique class of two-dimensional nanoscale materials possessing properties such as single-crystalline quality, well-defined chemical composition, and extremely high anisotropy.[9–12] Pioneering work has been done on the oxide nanosheets and they show excellent electronic and magnetic properties including high dielectric constants and gigantic magneto–optical effects compared with conventional nanocrystallites and bulk materials.[10,13]
Ta2O5 nanosheets can be used as building blocks to fabricate nanostructured materials applied to electronic devices. However, the electronic performance could be seriously affected by various defects.[14–16] Some defects occur because of the diffusion of oxygen into tantalum, resulting in interstitial oxygen defects, and oxygen substoichiometry, resulting in oxygen vacancies.[17,18] Due to these defects, leakage current will occur in the oxide gate dielectric layer. Therefore, the investigation of defect properties in Ta2O5 nanosheets is of significant importance. Deep-level transient spectra (DLTS) and thermally stimulated current (TSC) are two general methods used to measure the electrical levels of thin-film defects. Since the former needs to form an Ohmic contact for the sample bottom electrode and the latter is mostly used for powder or liquid, they are unsuitable for nanosheets. Nondestructive and noncontact spectroscopic ellipsometry (SE) can detect the defect states and energy levels of high-κ film, which has been proposed in previous work.[18] Ellipsometry can investigate the dielectric properties of thin film by detecting the phase information and polarization state of light, and the thickness measurement can reach angstrom resolution.[19–21]
In this paper, the fabrication of single layer two-dimensional Ta2O5 via assemblies of nanosheets is introduced in the beginning, and then atomic force microscopy (AFM), x-ray photoelectron spectroscopy (XPS), and SE fitting are performed on samples. A key feature of this paper is the use of SE to investigate the electrical defects levels of single layer Ta2O5. The electrical levels of different charged oxygen vacancies will be shown by detailed SE fitting using the Lorentz oscillator model.
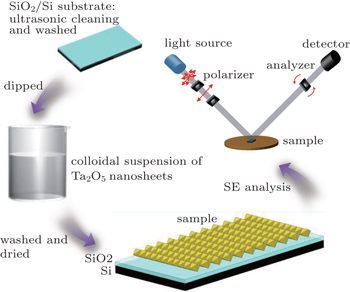
SiO2/Si substrates (SiO2 ∼ 127-nm thick) were washed with acetone by ultrasonic cleaning in wet sinks for 15 minutes, followed by ultrasonic cleaning again with alcohol for 5 minutes. After being washed thoroughly with deionized water, the SiO2/Si substrates were dipped in a colloidal suspension of Ta2O5 nanosheets for 20 minutes, followed by washing with copious water, as shown in Fig.
Samples were dried before characterization. In order to measure the surface morphologies and edge thicknesses of different samples, AFM was performed under ambient conditions, using a Veeco MultiMode VIII instrument equipped with a Nanoscope V controller. XPS was performed on samples to analyze the chemical structures. SE data were measured by a GES-5E spectroscopic ellipsometer made in France at the Sopra company with a rotating analyzer and a polarizer at an incidence angle of 75˚ in the visible range (260 nm–800 nm).
Figure
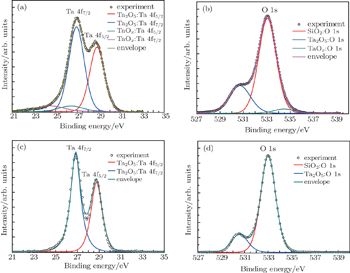
To characterize the chemical state of the single layer Ta2O5, XPS analysis was performed on samples dipped for 20 minutes. Figure
To investigate the defect states and energy levels of single layer Ta2O5, we measured SE of samples 1–3, as shown in Fig.
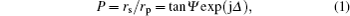
 | Fig. 4. Experimental and modeled values for the ellipsometric parameters Ψ and Δ for different samples dipped for 20 minutes: (a) sample 1, (b) sample 2, and (c) sample 3, respectively. |
The XPS results indicate that oxygen vacancies exist in as-grown single layer Ta2O5, thus the measured SE data can be fitted by adopting the Lorentz oscillator model to characterize the dispersion model of the Ta2O5 layer described as follows:
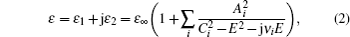
Three oscillators are used in the data analysis with key parameters listed in Table
| Table 1. Main parameters of the fitting results for all samples using the Lorentz oscillator model. . |
The oscillator energies Ci for all samples converge to three dominant values, with averages of 5.17, 4.05, and 2.17 eV, as listed in Table
 | Fig. 5. (a) Three-dimensional schematic representation of Ta2O5 atomic structure. Tantalum and oxygen atoms are shown in red and blue, respectively. (b) Band structure of single layer Ta2O5. |
According to the definition of the Lorentz oscillator model, parameter Ai expresses the probability of the electronic transitions from the conduction band to the valence band or defect traps. From Table
In conclusion, the properties of single layer two-dimensional Ta2O5 fabricated via assembling nanosheets were investigated by AFM, XPS, and SE. The results of XPS analysis indicate that oxygen vacancies exist in as-grown single layer Ta2O5, and SE fitting using the Lorentz oscillator model calculates the different transition energies and corresponding probabilities for two different charged oxygen vacancies. Via a comparison of the probabilities, the dominant defect configuration is obtained. In addition, the thicknesses of different samples calculated by spectroscopic ellipsometry fitting exhibit good agreement with atomic force microscopy measurement. Therefore, nondestructive and noncontact SE is appropriate for detecting the defect states and energy levels of single layer Ta2O5.
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 | |
| 18 | |
| 19 | |
| 20 | |
| 21 | |
| 22 | |
| 23 | |
| 24 | |
| 25 | |
| 26 | |
| 27 | |
| 28 | |
| 29 | |
| 30 |