Cite this Article
Pan Yuhao, Lei Bao, Qiao Jingsi, Hu Zhixin, Zhou Wu, Ji Wei. Selective linear etching of monolayer black phosphorus using electron beams. Chinese Physics B, 2020, 29(8): 086801  
Permissions
Selective linear etching of monolayer black phosphorus using electron beams
Pan Yuhao1, Lei Bao2, 1, Qiao Jingsi1, Hu Zhixin3, Zhou Wu2, Ji Wei1, ‡
Department of Physics and Beijing Key Laboratory of Optoelectronic Functional Materials & Micro-Nano Devices, Renmin University of China, Beijing 100872, China
School of Physical Sciences and CAS Center for Excellence in Topological Quantum Computation, University of Chinese Academy of Sciences, Beijing 100190, China
Center for Joint Quantum Studies and Department of Physics, Institute of Science, Tianjin University, Tianjin 300350, China

 

† Corresponding author. E-mail: wji@ruc.edu.cn

Project supported by the National Natural Science Foundation of China (Grant Nos. 11622437, 61674171, 11804247, and 11974422), the Strategic Priority Research Program of Chinese Academy of Sciences (Grant No. XDB30000000), Key Research Program of Frontier Sciences, Chinese Academy of Sciences (B.L, W.Z.), the Fundamental Research Funds for the Central Universities, China, and the Research Funds of Renmin University of China [Grant Nos. 16XNLQ01 and No. 19XNQ025 (W.J.)].

Abstract

Point and line defects are of vital importance to the physical and chemical properties of certain two-dimensional (2D) materials. Although electron beams have been demonstrated to be capable of creating single- and multi-atom defects in 2D materials, the products are often random and difficult to predict without theoretical inputs. In this study, the thermal motion of atoms and electron incident angle were additionally considered to study the vacancy evolution in a black phosphorus (BP) monolayer by using an improved first-principles molecular dynamics method. The P atoms in monolayer BP tend to be struck away one by one under an electron beam within the displacement threshold energy range of 8.55–8.79 eV, which ultimately induces the formation of a zigzag-like chain vacancy. The chain vacancy is a thermodynamically metastable state and is difficult to obtain by conventional synthesis methods because the vacancy formation energy of 0.79 eV/edge atom is higher than the typical energy in monolayer BP. Covalent-like quasi-bonds and a charge density wave are formed along the chain vacancy, exhibiting rich electronic properties. This work proposes a theoretical protocol for simulating a complete elastic collision process of electron beams with 2D layers and will facilitate the establishment of detailed theoretical guidelines for experiments on 2D material etching using focused high-energy electron beams.

PACS: ;68.65.-k;;68.37.Ma;;68.35.bg;
Keyword:;electronic beam radiation simulation;;black phosphorus;;chain vacancy;
1. Introduction

Since graphene monolayers were first exfoliated,[1–5] two-dimensional (2D) materials have received extensive attention[6–11] owing to their unique physical and chemical properties as well as potential applications.[12–19] Defects are inevitable in 2D materials and may play key roles in tailoring their physical and chemical properties.[20–26] For example, vacancies and domain boundaries, as two typical types of defects in transition metal dichalcogenide (TMDC) monolayers, often show specific local electronic[21] and magnetic structures[21,23] and even localized excitons.[25] However, it has long been a challenge to introduce and modify functional defects in a feasible and controllable manner.[27–30]

Focused electron beams have emerged as a possible means of manipulating individual atoms on the atomic scale, benefitting from the development of scanning transition electron microscopy (STEM). Various defects, even those stabilized only under extremely non-equilibrium conditions, such as multiple vacancies in graphene[31,32] and anti-site defects in MoS2,[21,33] have been successfully obtained using focused high-energy electron beams (FHEEBs) with kinetic energies greater than 60 keV.[27] The stable non-equilibrium state is an inherent benefit of material preparation using FHEEBs rather than conventional synthesis methods.[34–39] FHEEBs are also capable of creating much larger defects from intact layers, e.g., boundaries in TMDCs[39] and narrow nanoribbons of graphene.[36] However, the vacancies created in 2D materials, e.g., graphene and TMDCs,[22,31] are usually randomly distributed, and only the statistics method could be employed to perform analysis.[21,34,36] In other words, their formation process is complicated, and it is very expensive to capture the dynamic trajectories experimentally. In light of these challenges, insights from theoretical simulations have been of paramount importance to the field of atomic manipulation using FHEEBs.

A 2D material of great interest, black phosphorus (BP) has recently been found to exhibit excellent mechanical and electronic properties,[40–45] which could also be manipulated by FHEEBs.[46] A previous work revealed the dynamic stabilities of single-atom defects and edge atoms under FHEEBs.[47] However, the development of these defects and edges was not considered in detail, although this development determines the final type of the defect formed. In this paper, we focus on the evolution of a defect from a single-atom vacancy under a FHEEB in monolayer BP and predicted the final formation of a chain vacancy, composed of two parallel zigzag edges along the (100) direction. During the evolution, P atoms in the same zigzag chain along the (100) direction tend to be struck away one by one because the displacement threshold energies (Td) of these atoms are 8.55–8.79 eV, always lower than those along other directions during the vacancy evolution. The zigzag-like chain vacancy exhibits rich electronic properties. Firstly, there are clear antibonding- and bonding-like states along the chain vacancy, indicating that the interaction between the two edges of the vacancy is a new kind of covalent-like quasi-bonding (CLQB). Secondly, structural ups and downs are formed with an obvious bandgap of 0.13 eV opened, which is a typical characteristic of a charge density wave (CDW). This work provides a more comprehensive protocol for modelling the elastic collision process of high-energy electrons with 2D layers and is expected to inspire future works that will provide detailed theoretical guidance for experiments in the field of 2D material etching by FHEEBs.

2. Methods
2.1. Density functional theory calculations

Our density functional theory (DFT) calculations were performed using a generalized gradient approximation for the exchange–correlation potential, the projector augmented wave method,[48,49] and a plane-wave basis set implemented in the Vienna ab-initio simulation package (VASP). Van der Waals interactions were considered at the vdW-DF level with the optB86b functional for exchange (optB86b-vdW),[50] which was found to be suitable for modelling the structural properties of BP.[40] The kinetic energy cut-off for the plane-wave basis set was set to 500 eV for the structural relaxation calculations. A 2 × 2 × 1 k-mesh was adopted to sample the first Brillion zone of a 7 × 5 supercell of monolayer BP. The shape and volume of the primitive cell were fully optimized, and all of the atoms in the supercell were allowed to relax until the residual force per atom was less than 0.01 eV/Å. The formation energy of the BP edges was derived from EForm = (EEdge − NPμP)/NP, where EEdge is the total energy of the edge and μP represents the chemical potential of one P atom in monolayer BP.

2.2. Ab-initio molecular dynamics simulations

In previous works, an ab-initio molecular dynamics (AIMD) method was proposed to simulate electron beam irradiation.[32,35,47,51] The effects of elastic collisions were assessed by evaluating the displacement threshold energy Td, which was defined as the minimum initial kinetic energy needed to displace an atom (referred to as a target atom in this paper) from its original site without it recombining with the vacancy. Although a finite temperature environment was previously considered by introducing the Debye model, the random thermal motions were not actually simulated.[32]

In this study, we considered the random thermal motions by introducing a canonical ensemble process at 300 K before performing simulations. To obtain Td, AIMD was used to simulate the structural response to incoming momentum transferred from the incident high-energy electron beams. The kinetic energy cut-off was set to 400 eV in the AIMD simulations.

The simulation process consisted of two steps. Firstly, a canonical ensemble molecular dynamics simulation was performed at 300 K for 4 ps with a time step of 1 fs to simulate a thermal vibration environment. To reduce the effects of velocity fluctuations, two extreme steps were conducted in the last 2 ps to continue the simulation, where the target P atom had the highest velocities along and against the normal vector of the BP monolayers (which could be defined as the z-direction). Secondly, in both cases, we introduced an additional initial velocity along the −z direction toward the target P atom to simulate the instantaneous momentum transfer from the downward electron beam. We then performed a microcanonical ensemble simulation for 0.8–2 ps with a time step of 0.5 fs and traced the trajectory of the target P atom to judge whether the atom was out of the lattice structure. Two criteria were used here: the displacement of the target atom and the displacement times the velocity of the target atom. The first criterion was set to 5 Å, and the second was estimated as 2 Å × 0.05 Å/fs because the interaction was too weak to attract the target P atom back to the original site in these cases. A binary search method was used to obtain the range of the transferred kinetic energy until the velocity resolution was less than 0.001 Å/fs (Td ∼ 0.1 eV). Finally, Td was calculated from the average of the threshold velocities in the two extreme cases.

A case with oblique electron beam incidence was also considered by introducing additional velocities tilted at 10° to the target atoms in the pristine BP monolayer. Oblique incidence did not effectively reduce the displacement threshold energies of the P1T1 atoms, which also had difficulty escaping. For P1D1, Td increased by 0.3–1.0 eV (tilted along four different directions (±1, 0, 0) and (0, ±1, 0)) compared to that in the vertical incidence case. To unify the standards, we evaluated the minimum Td in the above investigations, so only the vertical cases were considered.

The entire simulation process involved extensive labor. A control program, called the automatic beam effect simulation tool (aBEST), was thus written to implement the above process automatically by calling VASP within Python language. The aBEST and example files are accessible through https://gitee.com/jigroupruc/aBEST.

Performances of the optB86b-vdW, PBE-D3, and PBE functionals were examined by calculating Td for P1D2 and P2D1 of configuration V1P. The inclusion of van der Waals corrections reduces the estimated Td, i.e., from 6.68 eV and 8.55 eV of PBE to 6.57 eV and 7.10 eV of PBE-D3 and 5.88 eV and 7.42 eV of optB86b-vdW for atoms P1D2 and P2D1. However, their relative differences between atoms P1D2 and P2D1 are rather comparable, especially for those of PBE and optB86b-vdW. In light of this, the use of PBE, instead of optB86b-vdW, in DFT-MD simulations does not qualitatively change the conclusion of relative Td energies of different atoms, but saves the computational cost by roughly three times.

2.3. Electron beam threshold kinetic energy estimations

The electron beam threshold kinetic energy here is defined as the minimum electron beam kinetic energy required to knock out the target atom. In other words, the cross-section of the electron beam for the target atom becomes positive just at the threshold kinetic energy. The cross-section at a selected Td can be derived using the McKinley–Feshbach formalism[52] as

Here, Z is the proton number of the target atom (15 for P); ε0 is the vacuum permittivity; me and M are the masses of an electron and P atom, respectively; ve is the velocity of the electron before scattering; is the maximum energy transferred from an electron beam with a kinetic energy of Ee to the target P atom, and c is the velocity of light. As the cross-section was set equal to zero, electron beam threshold kinetic energy could be evaluated.

3. Results and discussion
3.1. Formation of a single vacancy

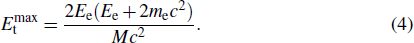
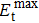
There are two kinds of P atoms in pristine monolayer BP when electron beams are incident from the top to bottom because of the symmetry of the geometry, as shown using different colors in Fig. 1(a). The two kinds of P atoms combine into two parallel zigzag-like chains.

Fig. 1. (a) Top and side views of atomic structure of monolayer BP (V0P). The names of the zigzag-like chains and two tested atoms are marked. The upper (colored in plum) and lower (colored in light coral) chains are named nT (n is the order number of the chain) and nD, respectively. The P atoms in the upper and lower sublayers are named PnTm (m is the order number of the atom) and PnDm, respectively. (b) and (c) Trajectories of two tested P atoms in pristine monolayer BP under an FHEEB. (d) Top and side views of the atomic structure of a single-atom vacancy BP (V1P) and all five tested P atoms. (e) Calculated cross-sections for the tested atoms in pristine monolayer BP (V0P) and single-atom vacancy monolayer BP (V1P).

The Td was calculated for two typical atoms (P1T1, P1D1) to compare their dynamic stabilities under the FHEEB. It is very difficult (Td > 19 eV) for the P1T1 atom (see Fig. 1(a)) to leave the BP monolayer because it collides with the P atom (P1D1) underneath (Fig. 1(b)), while P1D1 could depart from the layer much more easily (Td ∼ 9.03 eV) (Fig. 1(c)). The cross-sections were also calculated for the displacement of the two P atoms, as shown in Fig. 1(e) and Table 1. The P1D1 gives rise to a corresponding electron beam threshold kinetic energy of ∼ 114.8 keV, which is easily accessible by modern STEM.[53,54] There is enough time for structural relaxation of the lattice before the next electron beam irradiation in regular STEM.[32,47] We fully relaxed the single-atom vacancy of the monolayer BP (V1P) for the subsequent studies of the vacancy development, as shown in Fig. 1(d). In the V1P structure, P1T1 moves along the y-direction to neutralize the dangling bonds around P2D1 and P2D2.

Table 1.

Displacement threshold energy and corresponding minimum electron accelerating voltage for tested P atoms in V0P and monolayer BP with V1P, V2P, V3P, and V4P.

.
3.2. Vacancy development

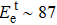
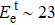
The chemical environments of the atoms surrounding the single-atom vacancy are very different from those in pristine monolayer BP. Td was calculated for five selected typical atoms to uncover the dynamic stability differences of the surrounding atoms. These five atoms represent three typical directions in which the vacancy could develop, as indicated in Fig. 1(d). The Td values and electron beam threshold kinetic energies of these five P atoms are summarized in Table 1 and depicted in Fig. 1(e). It is interesting that P1D2, the nearest P atom to the vacancy within the same zigzag chain, shows the smallest Td of 6.68 eV ( keV). For the other selected atoms, Td is at least 1.8 eV ( keV) higher than that of P1D2, which is enough to distinguish their dynamic stability under an FHEEB. Thus, P1D2 can be knocked out without removing the other atoms. A double-atom vacancy (V2P) is thereby formed. The surrounding atoms also move to neutralize dangling bonds in V2P after relaxation. In particular, P1D3 is obviously close to V2P and moves upwards along the (001) direction, as shown in Fig. 2(a).

Fig. 2. Atomic structures of BP with vacancies and zigzag chain vacancy. (a)–(c) Top and side views of atomic structures of BP with double-atom vacancy (V2P), triple-atom vacancy (V3P), and quadruple-atom vacancy (V4P) with the tested atoms marked on them. (d) Predicted zigzag chain vacancy in monolayer BP.

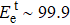
Continuing the vacancy development, Td and of five selected typical P atoms around the double-atom vacancy V2P (circled in Fig. 2(a)) were evaluated. Similarly to the V1P case, the nearest P atom (P1D3) to the vacancy along the same zigzag chain also has the smallest Td of 8.32 eV. Seven typical P atoms in a triple-atom vacancy (V3P) and five typical P atoms in a quadruple-atom vacancy (V4P) were also tested, as shown in Figs. 2(b) and 2(c). The simulation results indicate that P1D4 (Td ∼ 7.75 eV and keV) and P1D5 (Td ∼ 8.44 eV and keV) will be struck away in a row. The vacancy tends to be extended along this zigzag-like P atom chain under the FHEEB according to the above results.

The reason for this finding is associated with the local structures around the atoms, according to our observation of the atom trajectories. The atoms in the upper sublayers always have difficulty escaping because they would bond to or crash into the atoms in the lower sublayers although the electron beam breaks their bonds with other upper-layer atoms. Meanwhile, for the atoms in the lower sublayers, there are fewer atoms nearby to prevent them from escaping when they are near vacancies than in the pristine lattice. In other words, the closer an atom is to a vacancy, the less likely it is to be bonded with and transfer momentum to the surrounding atoms.

Based on these results, we also predicted that the vacancy would expand along a 1D zigzag chain and eventually become a zigzag chain vacancy (as shown in Fig. 2(d)) under an FHEEB. A double chain vacancy, which had high structural similarity to our predicted zigzag chain vacancy, was found in few-layer BP under an FHEEB in a recent experiment.[34] These experimental results confirm our prediction and verify the reliability of our method.

3.3. Electronic properties of the vacancy

The electronic properties of the zigzag chain vacancy were calculated for in-depth study. The differential charge density (DCD) indicated that the interaction between the two parallel zigzag edges is stronger than the van der Waals interaction because the electron charge significantly decreases near the interfacial P atoms and accumulates between them, as shown in Fig. 3(c). Furthermore, the band structure along the x-direction and partial charge density (PCD) are plotted to uncover the interaction between the two edges. As shown in Fig. 3(a), the chain vacancy has two metallic edge states, named MB1 and MB2. The PCDs of the two metallic states show clear antibonding-like (MB1) and bonding-like (MB2) states between the two zigzag edges (see Fig. 3(b)), illustrating that the two parallel zigzag edge states are hybridized with each other. The hybridization, however, is not as strong as a covalent bond because both states are half-occupied with a small energy reduction (72 meV/edge atom). A recently uncovered non-covalent interaction between two BP layers, covalent-like quasi-bonding CLQB,[40,55] offers new insight into the interactions between two BP layers, where the bonding and anti-bonding states are both fully occupied. Our findings help improve understanding of CLQB in which covalent-like states can also be half-occupied.

Fig. 3. Electrical properties of predicted zigzag chain vacancy in monolayer BP. (a) Band structure and density of states of the chain vacancy. (b) PCD at bands MB1 and MB2, DCD, and atomic structure of the zigzag edge chain. (c) Band structure of double-periodic chain vacancies with and without up-and-down distortion. (c) PCD at bands MB1 and MB2, DCD, and atomic structure of the zigzag edge chain. (d) Top view (left) and side view (right) of the atomic structure of the chain vacancy with distortion.

A CDW feature was also found in this zigzag chain vacancy. The cross-point of the Fermi level and MB2 was near the midpoint between points Γ and X. A double-periodic lattice was thus tested to look for the CDW according to the Fermi surface nesting theory in a one-dimensional system. The zigzag chain vacancy indeed spontaneously formed structural ups and downs with a tiny energy drop (only 4.3 meV/edge atom), as shown in Figs. 3(c) and 3(d). An obvious bandgap of 0.13 eV was also found to have opened, which is a typical characteristic of a CDW. The vacancy changed from a metallic to narrow gap system.

3.4. Thermodynamic stability

A zigzag edge is obviously not the only kind of edge in monolayer BP. Thus, the geometric structures of several possible edges were relaxed, and their formation energies were calculated to study the thermodynamic stability of our predicted vacancy. Along three crystal directions with low indices, as shown in Figs. 4(k)–4(o), five types of edges could be obtained, called Klein 110, Zigzag 110, Klein 100, Zigzag 100, and Armchair, with the top and side views shown in Figs. 4(a)–4(j). The sequence of their stabilities according our formation energy calculations was as follows: Klein 100 (0.43 eV/Å) > Klein 110 (0.45 eV/Å) > predicted chain vacancy (0.48 eV/Å) > Zigzag 100 (0.52 eV/Å) > Armchair (0.67 eV/Å) > Zigzag 110 (0.84 eV/Å).

Fig. 4. Five kinds of calculated edges in monolayer BP. Top views (a)–(e) and side views (f)–(j) of the atomic structures of the edges we focused on in monolayer BP. (k)–(o) Crystal directions of the corresponding edges.
4. Conclusion

A special zigzag chain vacancy in monolayer BP was predicted by using an FHEEB and knocking away P atoms one by one along a zigzag chain in the lower sublayers. The calculated electronic properties of the chain vacancy showed that there was quasi-bonding between the two edges of the vacancy, and a CDW was also formed along the vacancy. Our findings help improve understanding of quasi-bonding in which covalent-like states can also be half-occupied. The chain vacancy was a dynamically stable but thermodynamically metastable state according to our comparison of the stabilities of five typical edges in monolayer BP. It was inspiring that the electron beam could create a dynamically mostly stable but thermodynamically metastable vacancy, which is difficult to obtain using conventional chemical synthesis methods but easier to achieve using an electron beam, as stated above. This characteristic proves that an FHEEB can create a special environment for defect development. In addition, although the protocol provided in this work offers a route to more comprehensively capture the elastic collision process of defect formation in monolayer BP, the method is also subject to improvement with considering inelastic collisions (or electronic excitation process). Electronic excitation under electron beams is a complicated process which may involve phonon scattering,[56,57] intra- or inter-band transition,[58,59] plasmon,[60] among the others. A few previous methods do be available to simulate those excitation processes, like constrained density functional theory,[61] impulsive 2-state model,[62,63] non-adiabatic molecular dynamics,[64] and time-dependent density functional theory.[65] This work is expected to inspire further works that will implement those exciton modeling methods into the simulation protocol and thus provide detailed theoretical guidance for future experiments in the field of 2D material etching by FHEEBs.

Reference
[1] Katsnelson M I 2007 Mater. Today 10 20
[2] Novoselov K S 2005 Nature 438 197
[3] Geim A K Novoselov K S 2007 Nat. Mater. 6 183
[4] Hwang E H Das Sarma S 2008 Phys. Rev. 77 115449
[5] Geim A K Grigorieva I V 2013 Nature 499 419
[6] Wang Z M 2014 MoS2: Materials, Physics, and Devices Berlin Springer 10.1007/978-3-319-02850-7
[7] Wang Q H Kalantar-Zadeh K Kis A Coleman J N Strano M S 2012 Nat. Nanotechnol. 7 699
[8] Fivaz R Mooser E 1967 Phys. Rev. 163 743
[9] Vogt P 2012 Phys. Rev. Lett. 108 155501
[10] Houssa M 2011 Appl. Phys. Lett. 98 223107
[11] Bianco E 2013 ACS Nano 7 4414
[12] Berger C 2004 J. Phys. Chem. 108 19912
[13] Liao L 2010 Nature 467 305
[14] Schwierz F 2010 Nat. Nanotechnol. 5 487
[15] Radisavljevic B Radenovic A Brivio J Giacometti V Kis A 2011 Nat. Nanotechnol. 6 147
[16] Wang H 2012 Nano Lett. 12 4674
[17] Yoon Y Ganapathi K Salahuddin S 2011 Nano Lett. 11 3768
[18] Xia F Farmer D B Lin Y M Avouris P 2010 Nano Lett. 10 715
[19] Popov I Seifert G Tománek D 2012 Phys. Rev. Lett. 108 156802
[20] Banhart F Kotakoski J Krasheninnikov A V 2011 ACS Nano 5 26
[21] Hong J 2015 Nat. Commun. 6 6293
[22] Hong J 2017 Nano Lett. 17 3383
[23] Hong J 2017 Nano Lett. 17 6653
[24] Zhang C 2019 ACS Nano 13 1595
[25] Zhang S 2017 Phys. Rev. Lett. 119 046101
[26] Zhou W 2013 Nano Lett. 13 2615
[27] Susi T Meyer J C Kotakoski J 2017 Ultramicroscopy 180 163
[28] Zhao X 2017 MRS Bull. 42 667
[29] Ye G 2016 Nano Lett. 16 1097
[30] Ci L 2008 Nano Res. 1 116
[31] Kotakoski J Mangler C Meyer J C 2014 Nat. Commun. 5 3991
[32] Meyer J C 2012 Phys. Rev. Lett. 108 196102
[33] Komsa H P Krasheninnikov A V 2015 Phys. Rev. 91 125304
[34] Zhao J 2017 Small 13 1601930
[35] Susi T 2014 Phys. Rev. Lett. 113 115501
[36] Chuvilin A Meyer J.C Algara-Siller G Kaiser U. 2009 New J. Phys. 11 083019
[37] Zhang S Y X X Q Hua X M Xie Z L Liu B Chen P Han P Lu H Zhang R Zheng Y D 2014 Chin. Phys. Lett. 31 056802
[38] Deng Y Wang Y Li X L 2012 Chin. Phys. Lett. 29 086801
[39] Komsa H P Kurasch S Lehtinen O Kaiser U Krasheninnikov A V 2013 Phys. Rev. 88 035301
[40] Qiao J Kong X Hu Z X Yang F Ji W 2014 Nat. Commun. 5 4475
[41] Hu Z X Kong X Qiao J Normand B Ji W 2016 Nanoscale 8 2740
[42] Jia Q Kong X Qiao J Ji W 2016 Sci. Chin. Phys. Mech. & Astron. 59 696811
[43] Ren Y 2017 Chin. Phys. Lett. 34 027302
[44] Cheng F 2016 Chin. Phys. Lett. 33 057301
[45] Qiao J Zhou L Ji W 2017 Chin. Phys. 26 036803
[46] Xiao Z 2017 Nano Res. 10 2519
[47] Vierimaa V Krasheninnikov A V Komsa H P 2016 Nanoscale 8 7949
[48] Blöchl P E 1994 Phys. Rev. 50 17953
[49] Kresse G Furthmüller J 1996 Phys. Rev. 54 11169
[50] Klimeš J Bowler D R Michaelides A 2011 Phys. Rev. 83 195131
[51] Komsa H P 2012 Phys. Rev. Lett. 109 035503
[52] McKinley W A Feshbach H 1948 Phys. Rev. 74 1759
[53] Egerton R F 2012 Microsc. Res. Technique 75 1550
[54] Dellby N 2011 Eur. Phys. J. - Appl. Phys. 54 33505
[55] Qiao J 2018 Sci. Bull. 63 159
[56] Huo L H Xie G F 2019 Acta Phys. Sin. 68 086501 in Chinese
[57] Balandin A A 2008 Nano Lett. 8 902
[58] Grosvenor A P Biesinger M C Smart R S C McIntyre N S 2006 Surf. Sci. 600 1771
[59] Hilgendorff M Sundström V 1998 J. Phys. Chem. 102 10505
[60] Willets K A Van Duyne R P 2007 Annu. Rev. Phys. Chem. 58 267
[61] Kretschmer S Lehnert T Kaiser U Krasheninnikov A V 2020 Nano Lett. 20 2865
[62] Ji W Lu Z Y Gao H 2006 Phys. Rev. Lett. 97 246101
[63] Anggara K Leung L Timm M J Hu Z Polanyi J C 2018 Sci. Adv. 4 eaau2821
[64] Chu W 2016 J. Am. Chem. Soc. 138 13740
[65] Furche F Ahlrichs R 2002 J. Chem. Phys. 117 7433