† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant Nos. 61703281, 11547040, 61803266, 61503140, and 61873171), the PhD Start- Up Fund of Natural Science Foundation of Guangdong Province, China (Grant Nos. 2017A030310374 and 2016A030313036), the Science and Technology Innovation Commission of Shenzhen, China (Grant No. JCYJ20180305124628810), and the China Scholarship Council (Grant No. 201806340213).
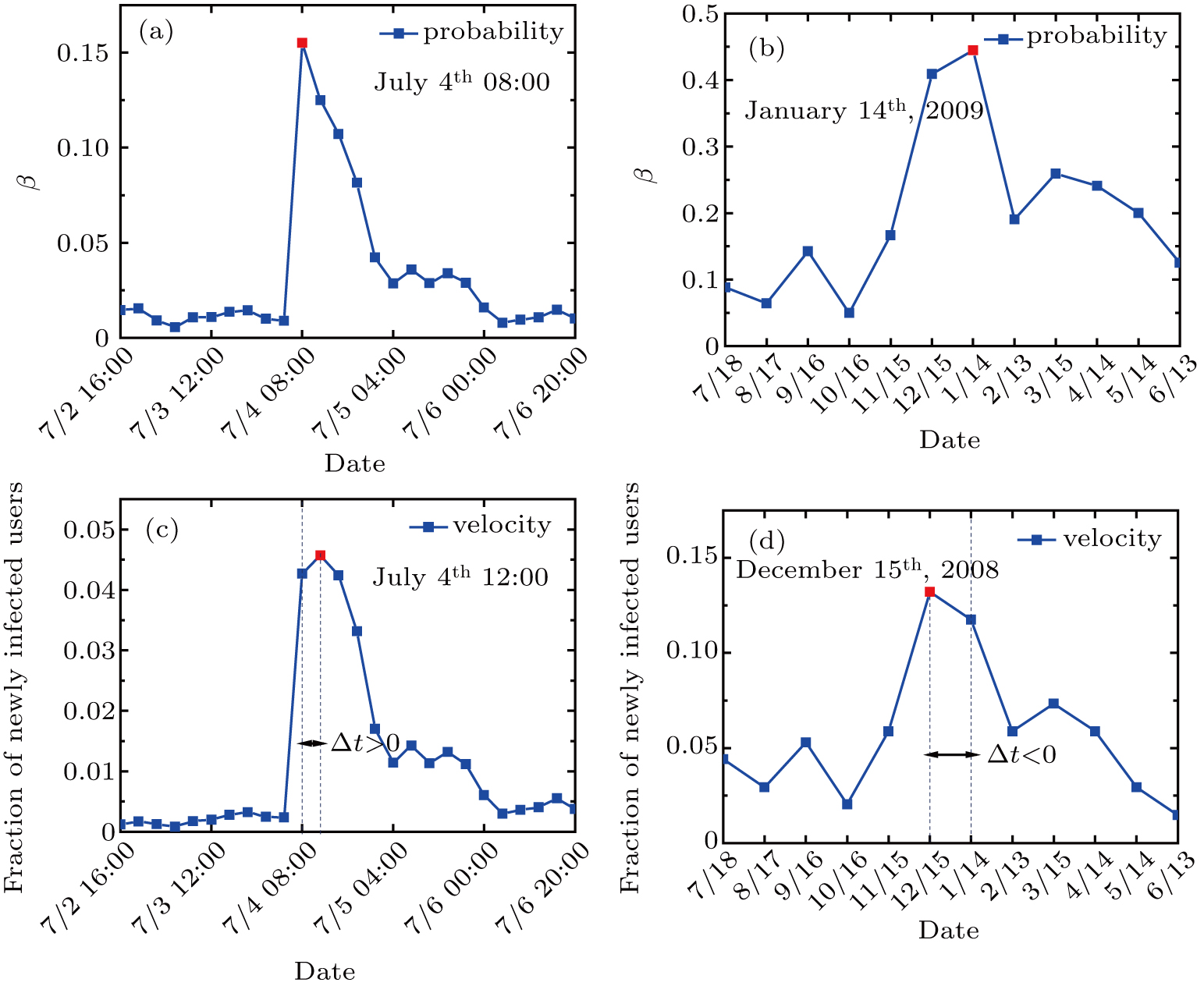
The potential mechanisms of the spreading phenomena uncover the organizations and functions of various systems. However, due to the lack of valid data, most of early works are limited to the simulated process on model networks. In this paper, we track and analyze the propagation paths of real spreading events on two social networks: Twitter and Brightkite. The empirical analysis reveals that the spreading probability and the spreading velocity present the explosive growth within a short period, where the spreading probability measures the transferring likelihood between two neighboring nodes, and the spreading velocity is the growth rate of the information in the whole network. Besides, we observe the asynchronism between the spreading probability and the spreading velocity. To explain the interesting and abnormal issue, we introduce the time-varying spreading probability into the susceptible-infected (SI) and linear threshold (LT) models. Both the analytic and experimental results reproduce the spreading phenomenon in real networks, which deepens our understandings of spreading problems.
In real systems, a mass of biological substance and virtual information spread among different social groups, such as causative agents,[1,2] plausible rumors,[3,4] and marketing messages.[5,6] Complex network is a simple but effective approach to the studies of ubiquitous propagation phenomena,[7,8] and has witnessed fruitful achievements in computer science, epidemiology, and other areas. For instance, the massive data collected from the online systems have revealed the underlying spreading mechanisms on the global scale,[9] helping manage the information diffusion[10,11] and better understand the spreading influence of nodes.[12–14] For some infrastructure and financial systems, studying the intricate interaction patterns between nodes conduces to the maintenance of perfect functions and resisting the risks.[15–17] Besides, another striking example is the critical threshold of the spreading probability below which the spreading process will spontaneously die away, otherwise it endangers the whole population.[18] It enlightens better immunization strategies by improving the critical value.[19,20] Therefore, the spreading issue provides a convenient access to understand the interplay between the network structures and functions.
Early works on the simple epidemic models solved the critical conditions for different regimes[21–24] and proved the non-trivial effects of the network structure and individual behaviors on spreading dynamics.[25–27] More recently, empirical researches developed classical models to describe the real spreading process. Min et al. combined the heterogeneous human activity patterns with the susceptible-infected (SI) model, resulting in the power-law decreasing spreading velocity in the long-time limit.[28] Gernat et al. extended the deterministic SI model on temporal networks, where the evolving contacts were comparable to the spreading dynamics. Compared with the randomized reference networks, they concluded that the inherent burstiness of the social interactions and the accelerated spreading process could co-occur in the bee communication network.[29] Wu et al. proposed a susceptible-accepted-recovered (SAR) model that considers information sensitivity and social reinforcement. The model reproduced main features of the real spreading events on Sina Weibo, the extremely fast or slow spreading process, by theoretical analysis and numerical simulations.[30] Vicario et al. found that the diffusion of conspiracy and scientific information among Facebook users shared the similar consumption patterns but showed different cascade dynamics.[31] To mimic the rumor spreading, they proposed a data-driven percolation model that demonstrates the decisive roles of homogeneity and polarization in predicting the cascade size. Mei et al. proposed a heterogeneous multi-stage model to investigate the impacts of the social reinforcement on spreading of information,[32] which hinders the diffusion process but facilitates the emergence of some hot spots. Besides, they maximized the spreading process with limited control sources by using Pontryagin’s maximum principle. Although the above-mentioned works have shed light on the real-world spreading mechanisms, there is still a lack of the knowledge of the evolution of the infection intensity and reaction rate of real spreading processes.
In this paper, we explore the information diffusion of real events on networks Twitter and Brightkite, and find that the spreading probability changes over time, which violates the constant transferring rate of standard spreading models. Beyond that, the empirical process shows the asynchronism that the maximal values of spreading probability and spreading velocity do not always occur simultaneously. To explain the phenomenon, we propose the improved SI and LT models based on the time-varying spreading probability. The analytic and experimental results show the time difference between the spreading probability and the spreading velocity, demonstrating the consistency of the empirical analysis and the proposed methods.
We use two datasets to study the empirical spreading process. Higgs recorded the activities of users on Twitter spanning from 1st to July 7th 2012,[33] before and after the official announcement of the Higgs boson on July 4th. Table
| Table 1. An example of user activities on Twitter. RT represents retweet and RE means reply. . |
| Table 2. The structural properties of the friendship networks, including the network size N, number of edges |E|, degree heterogeneity H = 〈 k2 〉/〈 k 〉2, average clustering coefficient 〈 C 〉, and network diameter D. . |
We use the SI model to analyze the empirical process on the social networks, where each node has two states: the infected (I) state and the susceptible (S) state. Initially, all nodes are in S state except a few particular infected ones. On Twitter, when a user receives the information, the user either accepts it or rejects (ignores) it. If the user retweets the information, we consider that it will be activated and become into the infected state. Similarly, the users on Brightkite can check in a place and share the location. If a user visits the same place according to his friends’ check-in information, the user will turn into the infected state. The spreading processes on Twitter and Brightkite are governed by[35]
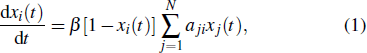
In the empirical analysis, it is difficult to calculate the transferring rate since each user may receive the information from multiple spreaders with introduces nonlinear phenomena. To simplify this issue, we evaluate the transferring rate as

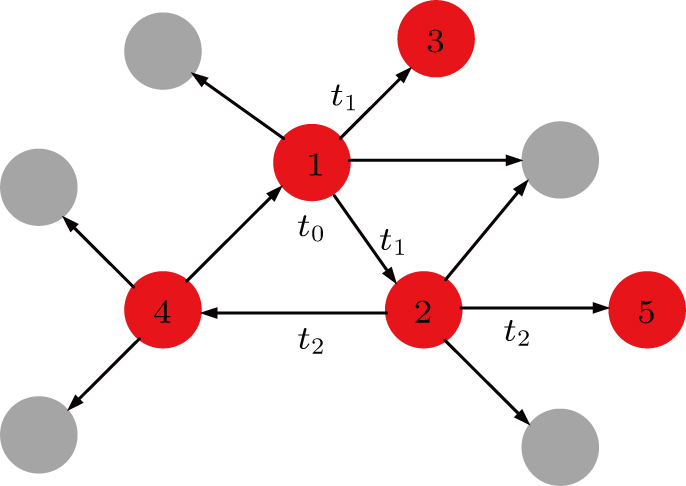
By tracking the propagation paths, figures
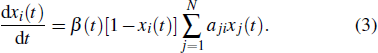
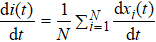
Initially, most nodes are in S state, xi(t)→ 0. Neglecting the higher-order xi(t)xj(t), we evaluate the early stage of the spreading dynamics in Eq. (
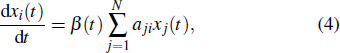

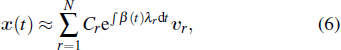
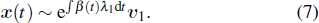
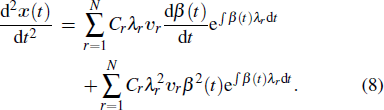
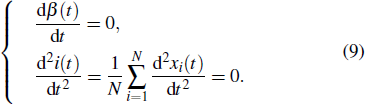
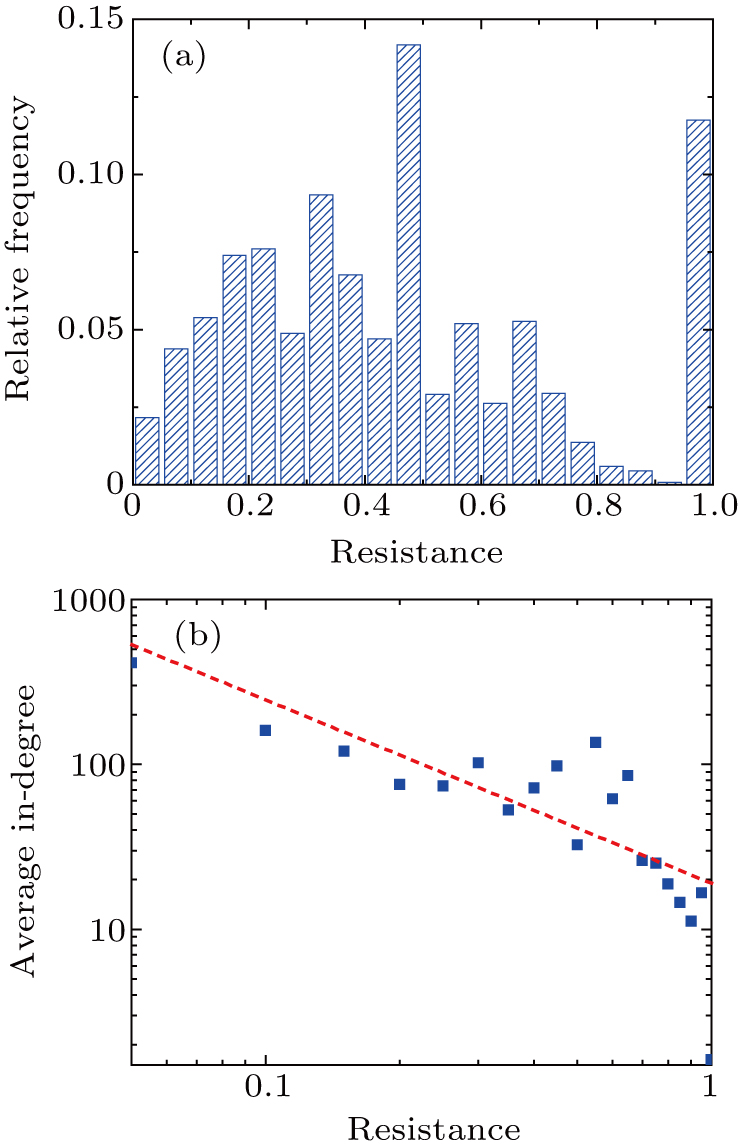
Apart from the SI model, the linear threshold model has also been widely used to imitate the information spreading dynamics on social networks. Here, we use the LT model to show that the results of this paper are not limited to the SI model and also hold on other spreading models. The SI model emphasizes the contact transmission in the epidemic process, while the LT model focuses on the accumulative effects of interactions and the collective behaviors of social groups.[38] In the LT model, every node is in one of the two states (S and I). Except for a few initial spreaders, the others are susceptible and endowed with the threshold values from the given distribution. At each time step, the susceptible nodes will turn into the infected state if the fraction of infected neighbors exceeds the threshold value. In some researches, the term ‘threshold’ sometimes refers to the critical condition of spreading processes. To avoid ambiguity, we use the personalized resistance to characterize the intrinsic threshold of the nodes.
The resistance has a significant influence on the spreading dynamics. We calculate the resistance hi of the user i who participates in the spreading of Higgs boson on Twitter[39]

With the assumption that the negative correlation leads to the asynchronism of the spreading process, we implement the LT model by the following steps:
Firstly generate the random sequence ϕ = [ϕ1,ϕ2,…,ϕN] following the given distribution. The smaller resistance is assigned to the larger degree node with the probability pi = ki/Σjkj. Select a proportion p of the nodes as the initial spreaders. At each step, the susceptible node observes the state of its neighbors and turns in to the infected state when the fraction of infected neighbors Ni/ki exceeds the resistance. Repeat step 3 until the spreading process stops.
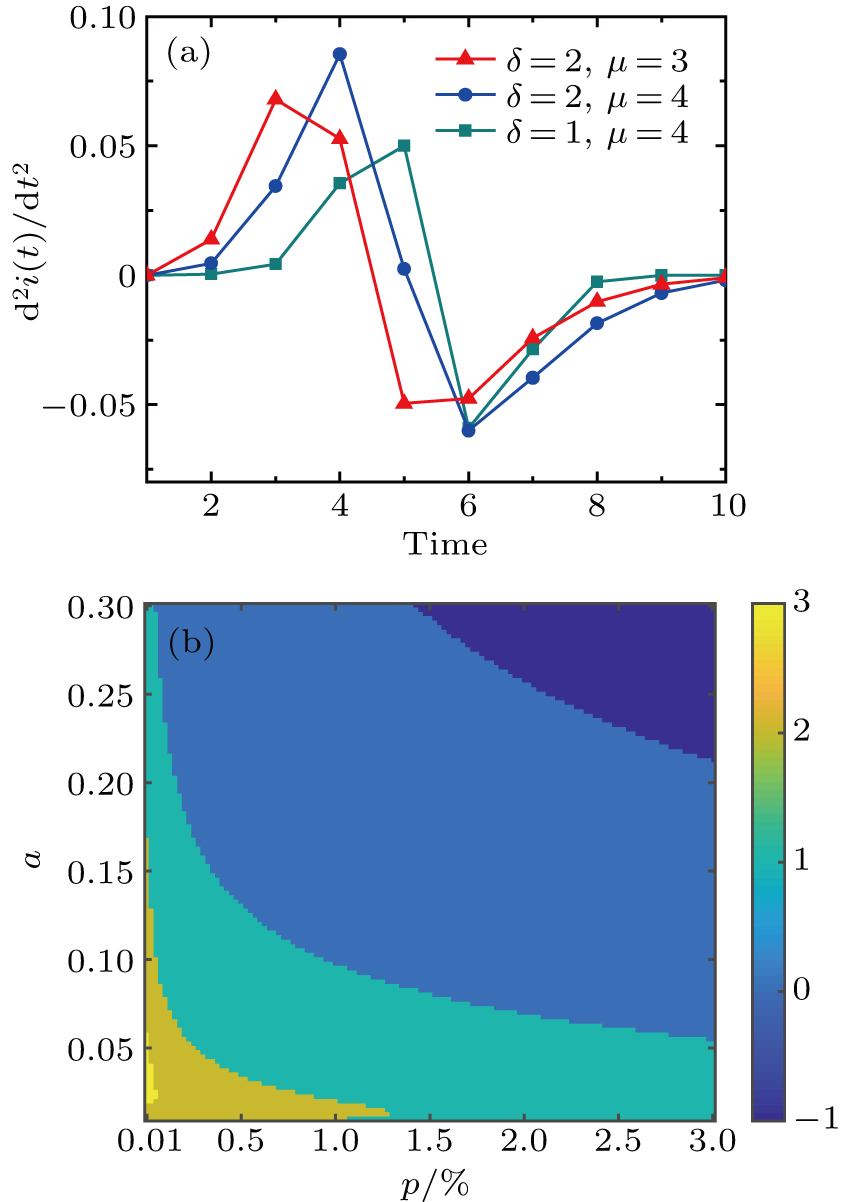
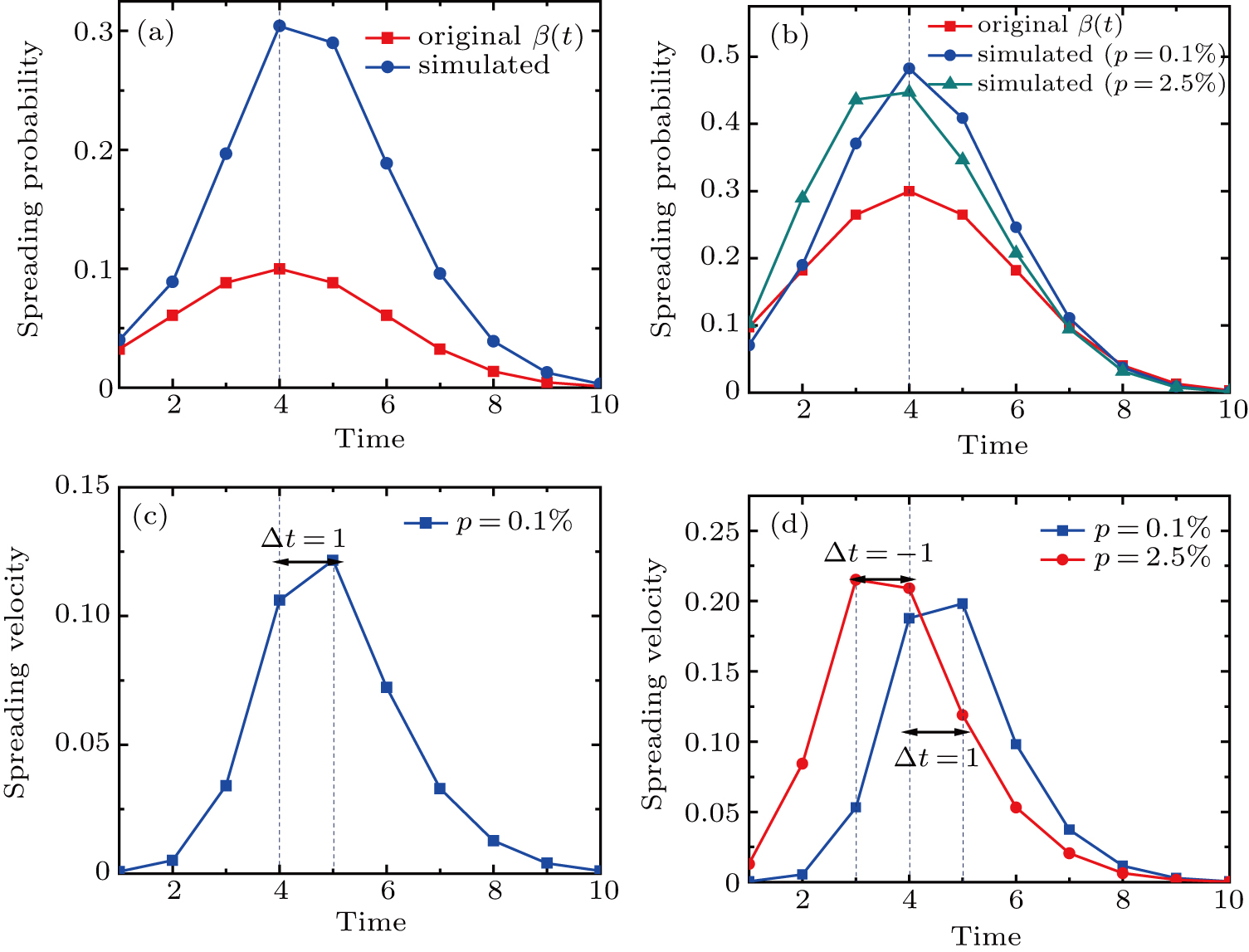
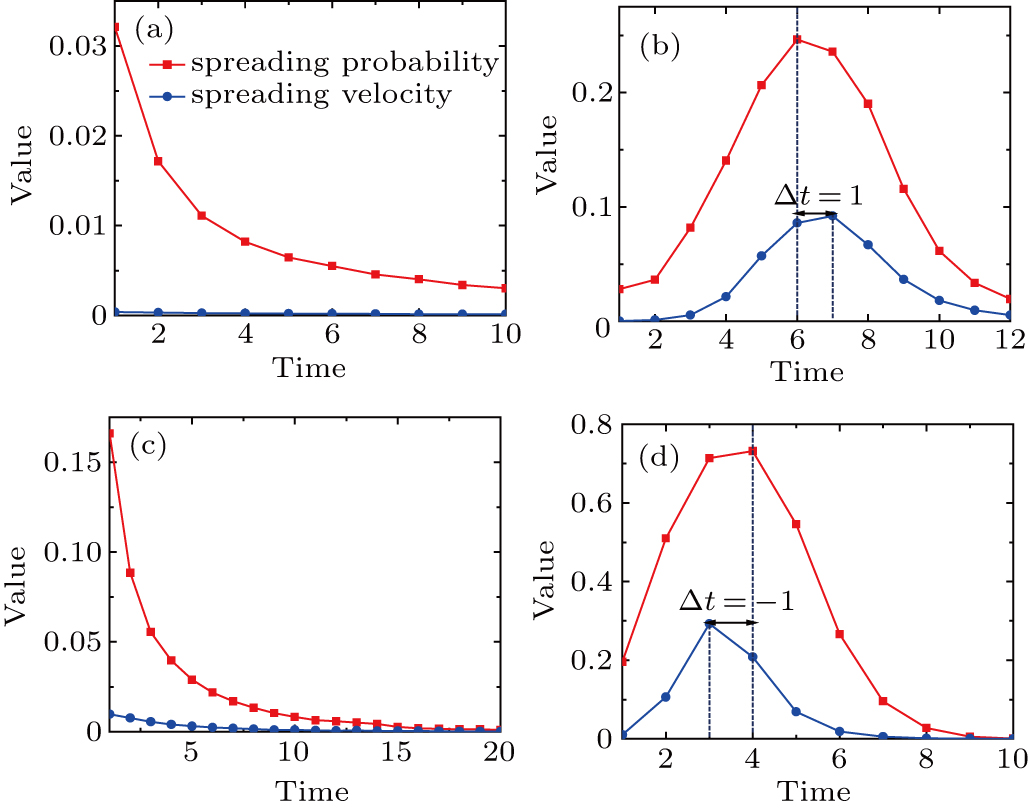
For the advanced SI model, we use the Gaussian-like distribution to approximate the bursty pattern and the dynamical spreading probability in Fig.

We first simulate the spreading process on the networks based on Eq. (
Furthermore, we simulate the advanced SI model under different conditions. Figures
To verify the impacts of the resistance on the spreading process, figure
Our work mainly explores the empirical spreading process on Twitter and Brightkite based on the propagation paths. The empirical analysis reveals the bursty spreading pattern, where we observe the asynchronism underlying the spreading process. However, the classical models cannot capture the time difference between the peak values of spreading probability and spreading velocity. By considering the time-varying spreading probability, we propose the improved SI and LT models to investigate the abnormal phenomenon, which provide analytical explanations and replicate the time difference that commonly exists in the real spreading process.
Understanding the spreading phenomena is of great significance to the diffusion efficiency. The asynchronism helps us determine better time to regulate the spreading process, making the promotions or updated innovations reach more people. Besides, the spreading paths suggest the temporal behaviors of users, especially during the outbreak period, which provide insights into the influence of users instead of purely structural information. Hence, our work not only enriches the knowledge of the complicated spreading mechanisms but also has widely potential applications to dissemination management and leadership identification.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] | |
| [39] | |
| [40] |