Cite this Article
Lu Xiao-Yong, Yuan Cheng, Zhang Xiao-Zhang, Zhang Zhi-Zhong. Hybrid-PIC/PIC simulations on ion extraction by electric field in laser-induced plasma. Chinese Physics B, 2020, 29(4): 045201  
Permissions
Hybrid-PIC/PIC simulations on ion extraction by electric field in laser-induced plasma
Lu Xiao-Yong1, 2, Yuan Cheng1, 2, Zhang Xiao-Zhang1, †, Zhang Zhi-Zhong2
Department of Engineering Physics, Tsinghua University, Beijing 100084, China
Science and Technology on Particle Transport and Separation Laboratory, CNNC, Tianjin 300180, China

 

† Corresponding author. E-mail: zhangxzh@mail.tsinghua.edu.cn

Abstract

The processes of electric ion extraction from plasma induced by pulse lasers are simulated by particle-in-cell (PIC) method and hybrid-PIC method. A new calculation scheme named preprocessing hybrid-PIC is presented because neither of the two methods above is omnipotent, especially under the circumstance of high initial plasma density. The new scheme provides credible results with less computational consumption than PIC method in both one- and two-dimensional simulations, except for Π-type electrode configuration. The simulation results show that the M-type performs best in all electrode configurations in both high-density and low-density plasma conditions.

PACS: ;52.65.Rr;;52.65.Ww;
Keyword:;ion extraction;;particle-in-cell (PIC) method;;hybrid-PIC;;electrode configuration;
1. Introduction

Investigations of ion extraction in laser-induced plasma have been an important researching topic for their applications such as in ion plantation,[1] ion beam generation,[2,3] and nuclear fusion,[4,5] especially the laser isotope separation (LIS) process.[6–8] In the last several decades, an ion extraction method with the characters of short extraction time, simple structure and less influence on other processes was required, especially under the circumstance of high-density plasma (∼1011 cm−3) and big size (several centimeters) for commercial values. Several extraction configurations meeting these requirements were reported. It should be noted that the experimental setups become complex and the ionization is disturbed due to the Zeeman effect if magnetic field is adopted, though it may be conducive to breaking the plasma shielding. Therefore, ion extraction by electric field is a common method in both theoretical and experimental researches.

In the early time, Chen[9] and Okano[10] have analyzed the ion extraction process theoretically and Okano derived a simplified formula that can describe extraction time of one-dimensional parallel plate condition. With the development of experimental and computational technology, Yamada et al. have investigated the extraction properties of several electrode configurations experimentally, such as parallel type, Π-type and alternately biased parallel type.[11–14] Scaling laws between ion-extraction time and applied voltage (0.5 kV–4.0 kV), plasma width (2 cm–9 cm), ion density (2 × 108 cm−3–2 × 1010 cm−3) were formulated. Nishio et al. presented a new conceptual electrode system, designated as ‘M-type electrodes’.[15] Rapid ion extraction is possible in the M-type system compared with that in the parallel type system. In theoretical researches, fluid model and particle model based on particle-in-cell (PIC) are used as common models in plasma simulations.[16,17] However, computing divergences of continuum and momentum equations appear easily at discontinuities and the collision processes cannot be described truly in fluid model. Watanabe and Okano have performed one-dimensional PIC and two-dimensional hybrid-PIC simulation and good agreement with the empirical formula given by Okano previously.[18] Ogura et al. calculated gadolinium ion extraction by the two-dimensional hybrid-PIC method, and the results were consistent with the experimental results.[19] Besides, some improved approaches such as two-region PIC[20] and two-system PIC[21,22] that appeared in recent years, provide new ideas for further simulating the ion extraction.

However, both simulations and experiments above were carried out under the circumstance of the low ion density (107 cm−3–1010 cm−3). The high-density ion extraction (∼ 1011 cm−3), which is required for economic efficiency and production yield in laser isotope purification plants, has been studied rarely. On the one hand, large-scaled metal evaporation and laser devices are required for high-density ion extraction experiments. On the other hand, PIC method occupies a huge computation cost in high-density two- or three-dimensional plasma simulations and the errors accumulate gradually in transient simulations. Besides, the applicability of hybrid-PIC still needs to be verified due to the fact that its electron thermal-equilibrium assumption is made. Therefore, there are few researches of high-density big-sized ion extraction both in experiment and in theory.

In this article, we build PIC and hybrid-PIC codes in both one- and two-dimensional ion extraction simulations. Firstly, the applicability of the two methods are verified in one-dimensional simulations and the process of electric ion extraction is discussed. Then the preprocessing hybrid-PIC is presented to extend the applicability of PIC method. Next, the extraction times of several electrode configurations are presented for comparison between the results obtained in low and high density situations. Finally, some conclusions are drawn from the present study.

2. Methods

The PIC method and hybrid-PIC method in electrostatic model are used for electric ion extraction simulation. The algorithms of the two methods are based on three steps. First, spatial density distributions, ni and ne, are obtained from the positions of particles by particle-in-cell technique. Second, the Poisson equation, as shown in Eq. (1), is solved for spatial potential ϕ. Third, velocities and positions of particles are advanced to new ones after one time step due to the influence of the electric field, which is derived from the spatial potential. It should be noted that only ions undergo the first and third steps in the hybrid-PIC method. The electronic density can be obtained by solving Eq. (2) instead of particle-in-cell technique, as electrons are assumed to be in thermal equilibrium state. Both ions and electrons undergo the first and third steps in the PIC code.

where ϕ is the potential, ne and ni are the densities of ion and electron, Te is the electron temperature. e is the elementary charge, ε0 is the permittivity of vacuum and k is the Boltzmann constant. The Poisson equation in hybrid-PIC method is solved with Eq. (2) in each time step. Dichotomy method and Newton–Raphson method are adopted due to the nonlinear coupled equations. Boundary conditions of electrons are given in Eqs. (3) and (4), where S is the boundary of simulation region, Γe, vs, and Ne are the electronic flux density on the boundaries, average thermal speed, and total number of electrons in simulation region, respectively.

Figure 1 shows the typical diagrams of electric ion extraction of parallel type, alternately biased parallel type, Π-type, and M-type. The simulation parameters are as follows. Relative atomic mass of ion is M = 200. Electron temperature and ion temperature are Te = 0.5 eV and Ti = 0.1 eV. Initial bulk velocity of plasma is vp = 0 m/s. Length of left/right plate is H = 6 cm. Length of upper plate, which equals to the distance between left and right plate, is L = 5 cm. Upper plate lies at a height of 2 cm above left/right plate and the length of M-plate is 5 cm. Size of plasma is Lp × Hp = 3 cm × 3 cm (width of plasma is Lp = 3 cm or 5 cm and distance between left and right plate is L = 5 cm in one-dimensional simulations). Initial plasma is uniformly distributed and lies in the center between left and right plates. Two initial plasma densities are 5 × 109 cm−3 and 1 × 1011 cm−3, and the corresponding applied voltages are 2.0 kV and 10.0 kV respectively. Unless otherwise specified, all the results in the following sections have experienced the test of super-particle number, cell size and time step.

Fig. 1. Typical diagram of electric ion extraction of (a) parallel type, (b) alternately biased parallel type, (c) Π-type, and (d) M-type.
3. Results and discussion

Both one- and two-dimensional simulation results are presented in this section. Only parallel type and alternately biased parallel type are displayed in one-dimensional simulations.

3.1. One-dimensional simulations

Five one-dimensional simulation cases are displayed to verify the applicability of PIC and hybrid-PIC method. The simulation parameters are listed in Table 1. Figure 2 shows the remaining ion/electron ratio as a function of extraction time in Case 1 and Case 2. Figure 3 shows the spatial evolution of electronic density and potential calculated by PIC method in the early extraction time in Case 2. The results of hybrid-PIC method is found to accord with those from the PIC method perfectly in Case 1, but not in Case 2. Their difference can be explained as follows. There exist three stages in electric ion extraction: (I) electron oscillation, (II) potential fall, and (III) sheath exfoliation, as shown in Fig. 2. Potential and electronic density oscillate violently when voltage is suddenly applied due to huge mass ratio between ion and electron as shown in Fig. 3. The first stage continues about hundreds of nanoseconds, in which duration the electrons which are located at the edges of plasma in the beginning, are absorbed by the electrodes easily. As a result, oscillation amplitude decreases gradually and the plasma potential may be higher than the voltage of anode plate. Then, ion extraction enters into the potential fall stage, which lasts about several microseconds. The extraction speed of electron is smaller than that of ion in this stage until the plasma potential drops nearly down to the voltage on anode plate, especially in Case 2. Finally, a plasma sheath is formed near cathode plate and then the sheath exfoliation stage begins. The region between two plates can be divided into two subregions, i.e., neutral plasma and sheath. In the neutral plasma there is no obvious electric field while in sheath region almost only ions exist, which are forced to move to cathode by electric field. As a result, the sheath is peeled constantly and the thickness of neutral plasma decreases until all ions and electrons are extracted entirely. The third stage continues dozens of microseconds, which occupies the majority of ion extraction time.

Fig. 2. Plots of remaining ion/electron ratio versus extraction time in (a) Case 1 and (b) Case 2.
Fig. 3. (a) Electronic density and (b) potential as a function of extraction time in Case 2.
Table 1.

Simulation parameters in one-dimensional simulation cases.

.

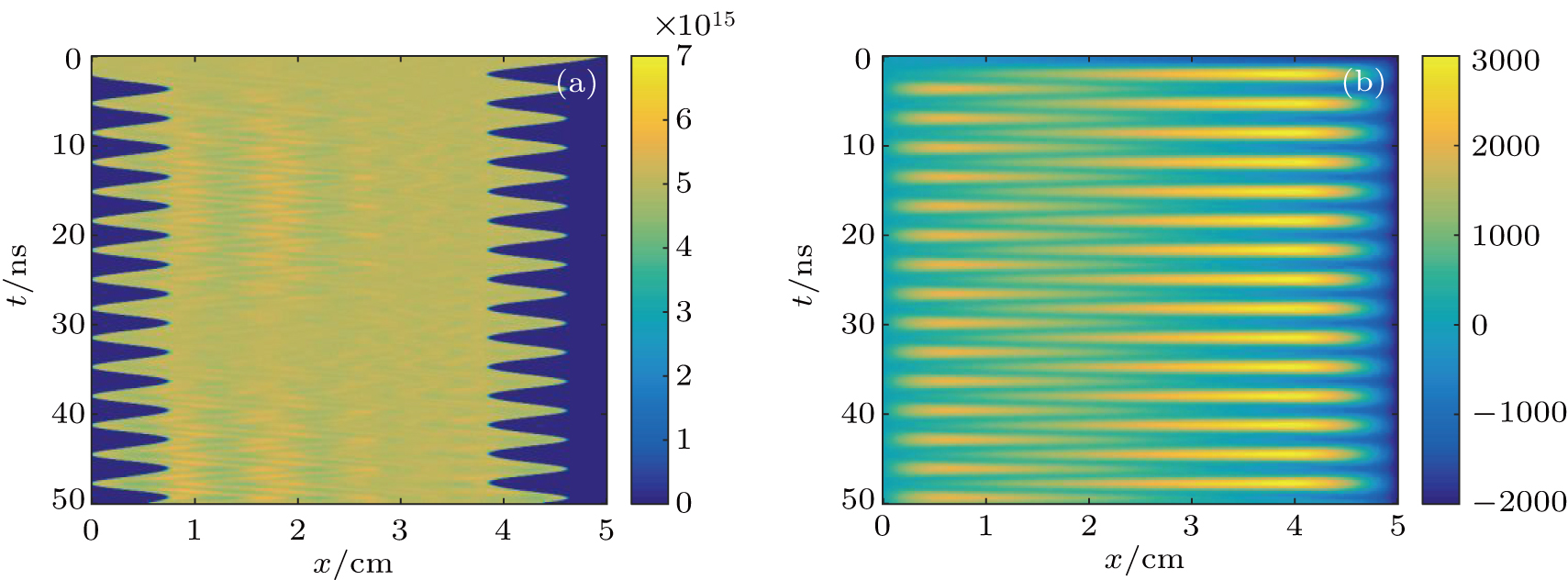
Obviously, the electron oscillation stage cannot be recognized in hybrid-PIC method because electronic motions are not taken into consideration. It means that the simulation results from hybrid-PIC method in Case 2 are incorrect because too many electrons are extracted in the first stage in practical processes. Therefore, the hybrid-PIC method is inapplicable to the circumstance that initial plasma is too close to the electrode plates. However, electron oscillates weakly in alternately biased parallel-type ion extraction because the voltage is increased slowly in the first stage. Therefore, two methods obtain almost identical results in Cases 3 and 4 as shown in Fig. 4, where the frequency and amplitude of applied voltage are 1.0 MHz and 2.0 kV respectively.

Fig. 4. Plots of remaining ion/electron ratio versus extraction time in (a) Case 3 and (b) Case 4.

Figure 5 presents the remaining ion ratio (Fig. 5(a)) and remaining electron ratio (Fig. 5(b)) as a function of extraction time in Case 5. Table 2 shows the computational consumptions in several simulation conditions. We can see that the computational consumption of PIC method is far larger than that of hybrid-PIC method. The results of PIC method approach to those of hybrid-PIC method gradually with the increase of super-particle number and decrease of cell size and time step. Consequently, it is unrealistic to simulate two- or three-dimensional high-density ion extraction by the PIC method for large computational and storage consumption. In general, the hybrid-PIC method cannot provide correct results in some simulation cases, and the PIC method cannot yield accurate results in an acceptable time in the high-density simulation case either.

Fig. 5. Plots of (a) remaining ion and (b) remaining electron ratio as a function of extraction time in Case 5.
Table 2.

Simulation parameters in one-dimensional simulation cases.

.

Based on the simulations and analyses above, we present a new scheme named preprocessing hybrid-PIC to solve the two problems above. The first stage of ion extraction is calculated by the PIC method and the rest two are calculated by the hybrid-PIC method because the electronic distribution satisfies the thermal-equilibrium assumption in the duration. The computational consumption of preprocessing hybrid-PIC is far less than that of the PIC method as the electron oscillation stage lasts only hundreds of nanoseconds. It should be noted that the deviation in the first stage obtained by the PIC method is insignificant due to its short duration, although none of super-particle number and others can meet the requirements of accurate simulation. Besides, the variation of electric field in plasma is selected to be the criterion for the method transformation. Finally, only total number of electrons and electron temperature are needed when hybrid-PIC method begins to be used, while none of the position and velocity of electron, and the plasma potential is taken into consideration. As shown in Fig. 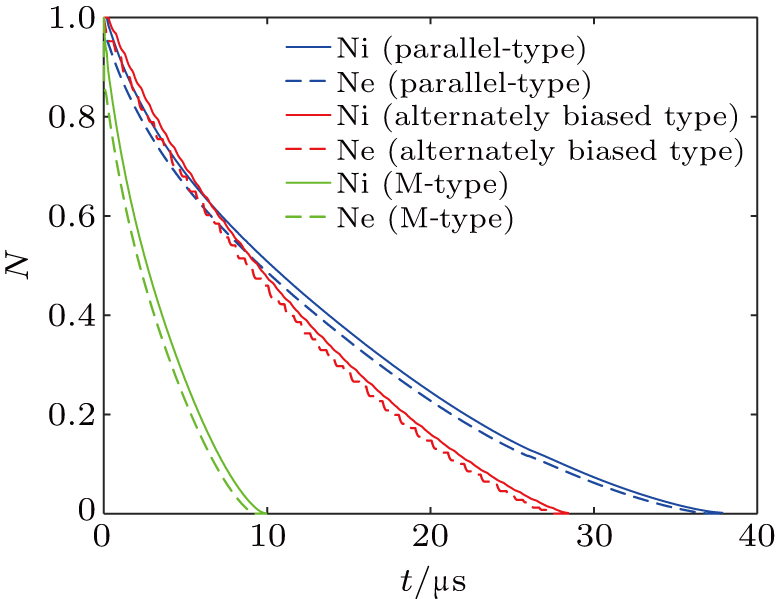2(b), the remaining ion/electron ratios obtained from preprocessing hybrid-PIC and PIC methods have no significant differences in Case 2 nor in other cases. As a result, the preprocessing hybrid-PIC scheme is effective in electric ion extraction simulations.

3.2. Two-dimensional simulations

In this subsection, two-dimensional simulations are carried out in four electrode configurations: parallel type, alternately biased parallel type, Π-type, and M-type, whose diagrams are shown in Fig. 1. Here we present the ion extraction results in Fig. 6 with an initial plasma density being 5.0 × 109 cm−3. The applied voltage is 2.0 kV. It should be noted that the correctness of two-dimensional code is proved by the comparison between two-dimensional periodic results and one-dimensional results. Besides, a bigger region is used in the simulations for solving the Poisson equation with the open boundary condition. Obviously, the preprocessing hybrid-PIC method provides almost identical results with those from the PIC method in the parallel type, alternately biased parallel type and M-type electrode configurations with much smaller (1/5 or 1/10) computational consumption, but not in the Π-type. This phenomenon can be explained as follows: there exists a potential well of several electron volts between upper plate and plasma indicated by the results from the PIC method as shown in Fig. 7. It is difficult for electrons to pass through the well to upper plate although the plasma potential is much lower than the ground potential. However, the potential well cannot be distinguished from the hybrid-PIC results because electrons are assumed to follow the Boltzmann relation in the whole simulation region, nor from the preprocessing hybrid-PIC. Therefore, the results of the Π-type, obtained under the thermal equipment assumption, are quite different from those from the PIC method. Numerical simulation of Π-type with high initial plasma density is still a problem.

Fig. 6. Plots of remaining ion ratio and remaining electron ratio versus extraction time in two-dimensional simulations for four electrode configurations: (a) parallel type, (b) alternately biased parallel type, (c) Π-type, and (d) M-type, with initial plasma density being 5.0 × 109 cm−3.
Fig. 7. Plots of potential at mid-line in Π-type PIC simulation for three different plasma potentials.

Figure 8 shows the remaining ion and electron ratio as a function of extraction time in the parallel type, alternately biased parallel type and M-type, obtained by the preprocessing hybrid-PIC method. The initial plasma density is 1.0 × 1011 cm−3, and the applied voltage is 10.0 kV. The simulation results show that the M-type presents the shortest extraction time in the three types above in the case of high initial plasma density, which are coincident with those in the case of low density. The potential difference between plasma and two cathodes are equal to the applied voltage in the M-type over the duration of extraction, and as a result, the ions can be extracted through the sheaths of two sides and by the M-plate simultaneously, which cannot do so by the remaining three types. As a result, M-type performs best because the extraction speed depends on the electric field intensity at the edge of plasma basically.

Fig. 8. Plots of remaining ion/electron ratio versus extraction time in two-dimensional simulations with initial plasma density being 1.0 × 1011 cm−3.
4. Conclusions

One- and two-dimensional particle simulations of ion extraction in laser-induced plasma are displayed by the PIC method and hybrid-PIC method. Three typical stages, electron oscillation, potential fall, and sheath exfoliation, are found to exist in electric ion extraction process. It shows that neither of the above two particle methods is perfect in some ion extraction simulation conditions, and the preprocessing hybrid-PIC are presented. Accurate results can be obtained by this new calculation scheme with less computational consumption than by the PIC method in one-dimensional simulations. In two-dimensional conditions, four electrode configurations, i.e., parallel type, alternately biased parallel type, Π-type, and M-type, are calculated under the circumstances of low and high initial plasma densities. The results show that the M-type has the best performance in all four configurations although the extraction time of high-density Π-type condition is unknown.

Reference
[1]Park Y Lee Y Chung K Hwang Y S 2011 Rev. Sci. Instrum. 82 123303
[2]Dudin S V Rafalskyi D V 2011 Eur. Phys. J. 65 475
[3]Vasquez M R Wada M 2016 Rev. Sci. Instrum. 87 02B924
[4]Mochalskyy S Wünderlich D Franzen P Fantz U Minea T 2014 Rev. Sci. Instrum. 85 02B301
[5]Mochalskyy S Lifschitz A F Minea T 2010 Nucl. Fusion 50 105011
[6]Kurosawa H Hasegawa S Suzuki A 2002 J. Appl. Phys. 91 4818
[7]Tamura K 2003 Vacuum 72 29
[8]Gundienkov V A Tkachev A N Yakovlenko S I 2004 Quantum Electron. 34 589
[9]Chen F F 1982 Phys. Fluids 25 2385
[10]Okano K 1992 J. Nucl. Sci. Technol. 29 601
[11]Yamada K Tetsuka T 1990 J. Appl. Phys. 67 6734
[12]Yamada K Tetsuka T Deguchi Y 1991 J. Appl. Phys. 69 8064
[13]Yamada K Tetsuka T 1991 J. Appl. Phys. 69 6962
[14]Yamada K Tetsuka T 1994 J. Nucl. Sci. Technol. 31 301
[15]Nishio R Yamada K Suzuki K 1995 J. Nucl. Sci. Technol. 32 180
[16]Tskhakaya D Matyash K Schneider R et al. 2007 Contrib. Plasma Phys. 47 563
[17]Verboncoeur J P 2005 Plasma Phys. Control. Fusion 47 A231
[18]Watanabe J Okano K 1993 Phys. Fluids 5 3092
[19]Ogura K Kaburaki H Shibata T 1993 J. Nucl. Sci. Technol. 30 1248
[20]Cohen B I Kemp A J Divol L 2010 J. Comp. Phys. 229 4591
[21]Wang W M Gibbon P Sheng Z M Li Y T 2015 Phys. Rev. 91 013101
[22]Wang W M Gibbon P Sheng Z M Li Y T 2015 Phys. Rev. Lett. 114 015001