† Corresponding author. E-mail:
The structure–activity relationship of functional materials is an everlasting and desirable research question for material science researchers, where characterization and calculation tools are the keys to deciphering this intricate relationship. Here, we choose rechargeable battery materials as an example and introduce the most representative advanced characterization and calculation methods in four different scales: real space, energy, momentum space, and time. Current research methods to study battery material structure, energy level transition, dispersion relations of phonons and electrons, and time-resolved evolution are reviewed. From different views, various expression forms of structure and electronic structure are presented to understand the reaction processes and electrochemical mechanisms comprehensively in battery systems. According to the summary of the present battery research, the challenges and perspectives of advanced characterization and calculation techniques for the field of rechargeable batteries are further discussed.
Nowadays, rechargeable batteries have occupied most portable electronics and electric vehicle markets, including lithium-ion batteries (LIB), lead-acid batteries, and so on.[1–3] To achieve better electrochemical performance and sustainable ability of rechargeable batteries, sodium-ion batteries,[4,5] metal–air batteries,[6] and many other secondary batteries[7,8] have been studied for a long time. A great many advanced characterization and calculation tools are employed to reach an in-depth understanding of the structure–activity relationship of battery materials in order to design and build satisfactory batteries to meet the urgent requirements of better electronics energy storage systems.[9–11]
From different viewpoints in the present characterization and calculation research for rechargeable battery materials, four fundamental scales including real space, energy, momentum space, and time are discussed in depth in this review. The real space structure such as crystal structure, phase interfaces, and defects greatly influences the practical performance of batteries. The electronic structure in momentum space and various energy level transitions are both closely related to the thermal, electric, and mechanical properties, which are different directions to explore the origin of function in battery materials. For the scale of time, time-resolved structure and electronic structure evolutions are another concern for both the industrial community and the academic community. By reviewing recent studies, the future prospects of characterization and calculation methods in multiple scales are discussed.
To explore the structure–activity relationship of materials, the characterization and calculation of real space information are the most intuitive choice that comes to mind. According to the demands for information on different length scales, researchers have utilized many different techniques to analyze the materials at the macroscopic level, crystal lattice level, and atom level.
The performances of rechargeable batteries are significantly influenced by macroscopic structure, such as the morphology of electrodes, the particle size and shape, and the property of the solid electrolyte interface (SEI). It is the reason why a great many useful characterization and simulation tools have been used to extract the macroscopic information.
Scanning electron microscopy (SEM) has been one of the most popular tools in investigating the macroscopic morphology and topography of battery materials by means of collecting secondary electrons and backscattered electrons. Combining with a microbattery design, it is feasible to achieve real-time observation of the microbattery during discharge and charge, which is called in situ or operando SEM.[12,13] But SEM can only acquire surface and topography information. In contrast, transmission electron microscopy (TEM) collects the transmission electrons and can provide internal information of materials, for example, the thickness of the shell in a core–shell structure nanoparticle.[14,15] Other methods to image the macroscopic morphology such as transmission x-ray microscopy (TXM)[16,17] have not been used comprehensively. In other words, SEM and TEM have dominated the field of macroscopic real space detection of battery materials because of their high spatial resolution and convenience, and other techniques are still needed to be studied and optimized.
Macroscopic level simulations can help us to understand macroscopic in-depth phenomena in rechargeable batteries, such as stress, thermal stability, flow, multi-field coupling, and failure mechanism. So far, researchers have used phase-field models to study grain growth and roughening, crack evolution, the interaction of dislocations and solute, electromigration, multicomponent interdiffusion, etc. For example, Zuo et al. put forward a phase-field model coupling lithium diffusion, stress evolution, and crack propagation.[18] The model was applied to a silicon thin film electrode to explore the coupling effects on diffusion and crack propagation paths. Hu et al. developed a phase-field based multiscale model that enables generating nanoporous microstructures of different porosity and connectivity patterns based on the depth and energy of the surface (pore/electrolyte interface) to predict both the microstructure patterns and the effective properties of heterogeneous solid electrolytes.[19] Zhang et al. developed a nonlinear phase-field model for predicting Li dendrite growth at the electrode/electrolyte interface during the electrochemical deposition involving highly nonequilibrium processes. In the model, the Butler–Volmer type electrochemical kinetics was automatically reproduced at the moving diffusion interface and a revised Poisson–Nesters–Planck equation was further solved for ionic transport and local overpotential variation.[20]
When the scale of the phase-field model is larger than the micron scale or the free-boundary condition is to be dealt with, the finite element method is a better choice. The finite element method can help to understand some macroscopic engineering problems, such as the thermal stability and mechanical failure mechanism of batteries. The temperature distribution in the batteries has a significant impact on their safety and longevity. Guo et al. used a finite element method to develop a three-dimensional thermal abuse model on LIB (Fig.
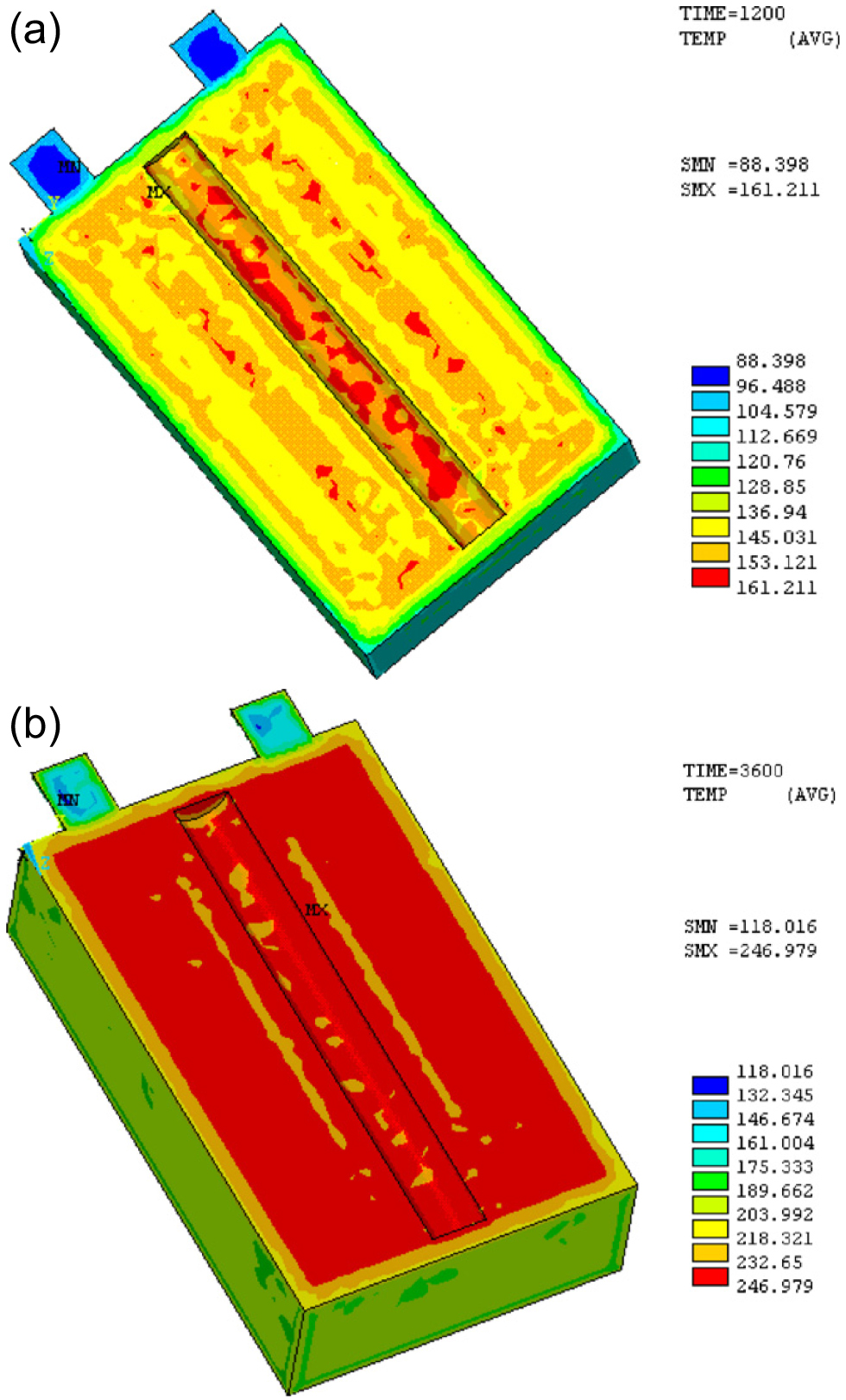 | Fig. 1. Distribution of temperature at 155 °C using finite element modeling among different time scopes: (a) 1200 s, (b) 3600 s.[21] |
Most of the active materials in batteries are crystal or short-range ordered amorphous materials. The ability to probe and simulate the crystal structure is critical for linking the electrochemical performances and materials’ structure. To date, the diffraction techniques such as x-ray diffraction (XRD), neutron diffraction (ND), and electron diffraction are the most powerful tools to study the crystal lattice by a basic principle: incident microscopic particle interacts with crystal atoms, resulting in wave interference effect. Different crystal planes have different atomic arrangements, thus different planes have various diffraction directions. The relationship between different crystal plane and diffraction direction is given by the famous Bragg’s law
 |
XRD utilizes x-rays (photons) as the incident particles. Collecting the data of θ and diffraction intensity and comparing them with standard substance information can provide the specific crystal structure and crystallinity of the sample. By Rietveld refinement, a great deal of useful information including lattice constant, atomic occupancy, and chemical stoichiometry of the material can be acquired to study the crystal structure and structure–activity relationship. It is worth mentioning that XRD provides the long-range average information because of the difficulty in converging the x-rays. On the other hand, in situ experiments are suitable for XRD. Synchrotron radiation source is able to offer higher intensity and photon flux than laboratory x-rays by several orders of magnitude. Combining synchrotron radiation source and in situ experiment techniques with XRD, real-time ultrafast data collection and deep penetration depth are satisfied with recent battery studies.[9]
Wu et al. demonstrated the crystal structure evolution of NaxCu0.27Zn0.06Mn0.67O2 (NCZM) during the charge and discharge procedures of the sodium ion batteries by in situ synchrotron XRD.[27] In the region of 0.51 < x < 0.78 of Fig.
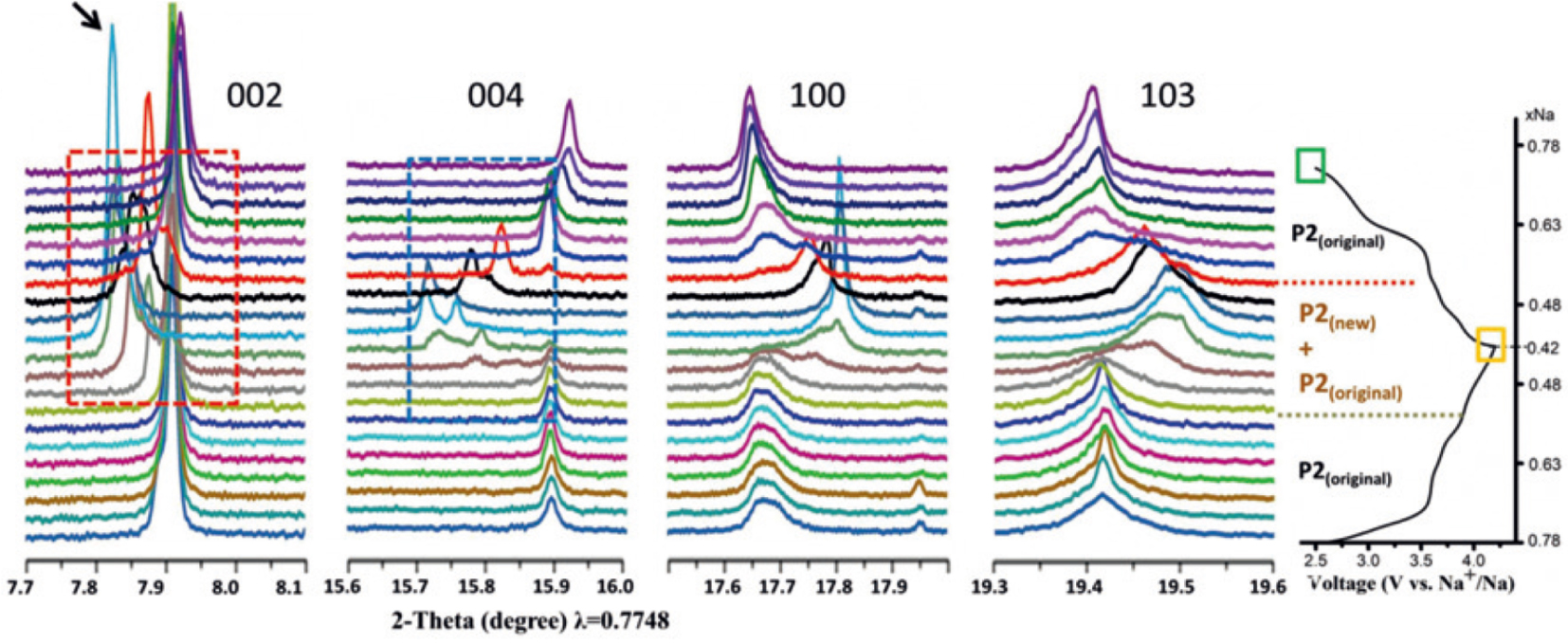 | Fig. 2. Selected regions of in situ synchrotron XRD data and the sodium content–voltage curve.[27] |
In contrast to x-rays, the scattering cross section of neutrons is irrelevant to atomic number Z, so it is better to distinguish light atoms and elements which have similar Z or isotopes than XRD. In addition, neutrons only interact with the atomic nucleus (different from x-rays that interact with electrons), resulting in a good penetration ability. However, there are some intrinsic limitations in ND. On the one hand, ND needs a large amount of materials. On the other hand, H atom strongly disturbs the analysis of the diffraction data. What is more, high-flux spallation neutron sources (SNS) which are urgently needed for ND technique are very scarce and the in situ experiments of ND are much more difficult than XRD.[9] To some extent, ND and XRD techniques complement each other in many different aspects.
Bruce’s group investigated Na2/3Ni1/3 − xMgxMn2/3O2 crystal lattice evolution with different substitution amount of Mg via ND and XRD.[28] Because of the different neutron scattering lengths of Mg and Mn, it is easy to characterize Mg2+/Mn4+ ordering by ND. The comparison between XRD and ND data is shown in Fig.
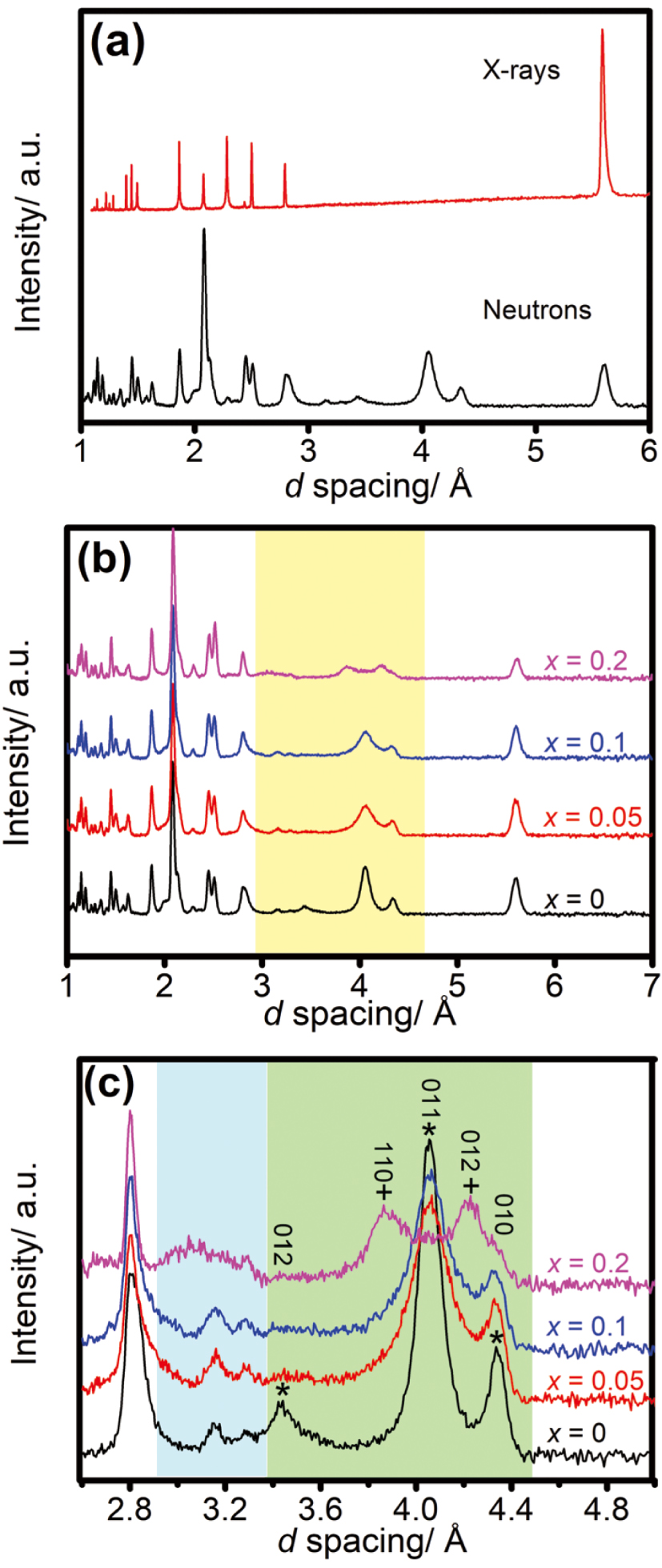 | Fig. 3. (a) X-ray and neutron diffraction data comparison for x = 0. (b) Neutron diffraction data for 0 ≤ x ≤ 0.2. (c) Zoomed-in yellow region of (b).[28] |
The principle of electron diffraction is similar to that of ND and XRD. Electron diffraction technique is always combined with TEM, thereby acquiring atomic and crystallographic information at the same time. The outstanding advantages of electron diffraction are the high intensity and the ability to analyze at nanoscale. However, the difficulties in quantitative analysis and the presence of the electron beam damage are still limiting this widely used diffraction technique. Nowadays, ultrafast electron diffraction (UED) technique equips with MeV electrons which differs from electron diffraction in TEM is used to study structural dynamics in many fields.[30–33] We will discuss more electron diffraction technique combing with TEM and electron energy loss spectrum (EELS) in the following section. In short, x-ray, neutron, and electron diffraction methods have their own respective advantages. Therefore, they are complementary techniques in detecting the crystal structure of battery materials to some extent.
In the field of simulation of crystal structure evolution, molecular dynamics and Monte Carlo simulations can both visually observe the migration of ions during electrochemical processes in the scale of crystal lattice level. Ma et al. created a dynamically adaptive approach in molecular dynamics simulations (Fig.
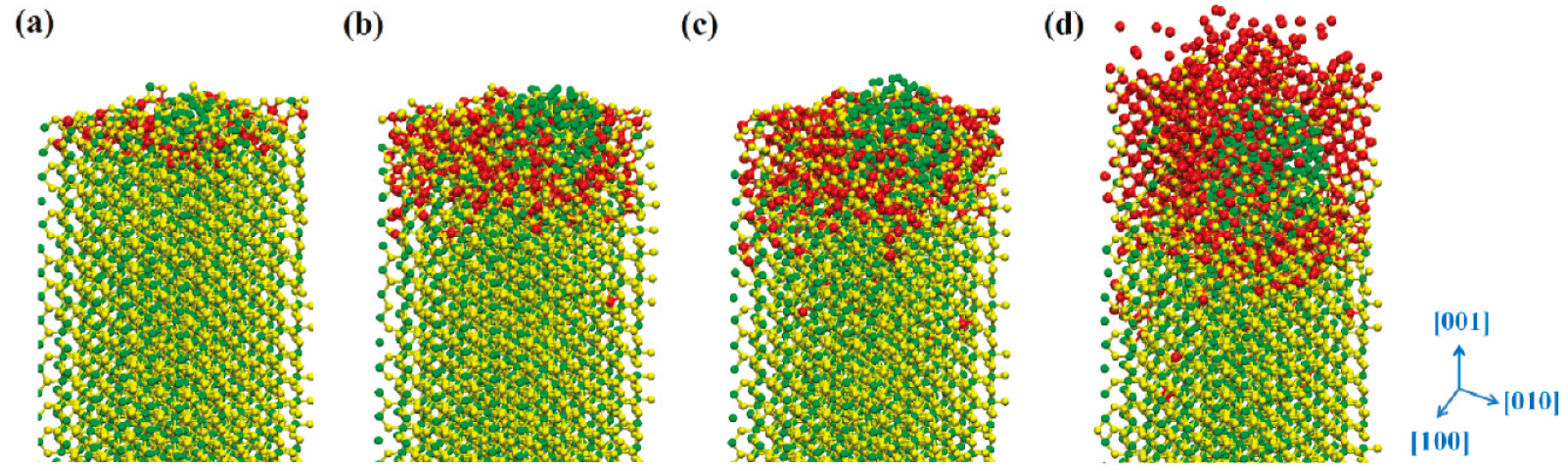 | Fig. 4. Simulated reaction between Li and FeF2 on the (001) surface of FeF2. Fe–F bond is yellow, and Li–F bond is red. (a) System with 72 Li+ already shows the growth of Fe metal cluster. (b) 288 Li+ with a glassy Li–F region. (c) 360 Li+, crystalline LiF is observed at the left corner. (d) 864 Li+, crystalline LiF grows.[34] |
The atomic structure of defects and interfaces has a great influence on the performance of full batteries, so the capability to probe atomic information of materials is essential for the performance optimization of batteries. To date, many microscopic techniques have achieved sub-nanometer or even sub-angstrom resolution with different methods, such as scanning probe microscopy (SPM), high-resolution transmission electron microscopy (HRTEM), and scanning transmission electron microscopy (STEM).
SPM includes scanning tunneling microscopy (STM), atomic force microscopy (AFM), etc. which are based on quantum tunneling effect or atomic force and have atomic resolutions. STM[36,37] and AFM[38,39] have already been used to observe the atomic structure of battery materials for a long time and brought a novel view for surface information, especially for the phase interface. However, SPM is limited to the surface region. Hence, the bulk atomic information of electrodes and solid-state electrolytes cannot be acquired by SPM. That is where the electron microscopy is required.
HRTEM is an atomic scale technique with a long history and it has the ability to probe bulk information. In brief, it is an imaging mode of TEM and can directly image atomic columns by phase interference between diffracted beams and transmission beams.[40] To confirm the existence of SEI between the Mo6S8 anode and aqueous electrolyte, Suo et al. directly observed the SEI via HRTEM which is shown in Figs.
 | Fig. 5. HRTEM images of (a) pristine Mo6S8 and (b) cycled Mo6S8.[41] |
Instead of utilizing the static incident electron beams of TEM, STEM scans the electron beams parallel to the optical axis and employs an annular detector to collect the scattered electrons.[40,43] Respectively, Pennycook et al. and Okunishi et al. proposed high angle annular dark field (HAADF)[44] and annular bright field (ABF)[45] imaging techniques in 1988 and 2009. The electron signal intensity in HAADF mode is almost proportional to Z1.7 which is suitable for imaging relative heavy atoms[46,47] and in ABF mode is approximate Z1/3 which is sensitive to light elements,[48] such as lithium and oxygen.
Gu’s group constructed an all-solid-state nanobattery that consists of a LiCoO2 cathode, Y and Ta doped LLZO solid-state electrolyte (Li6.75La2.84Y0.16Zr1.75Ta0.25O12), and a gold anode on a biasing nanochip by focus ion beam (FIB) milling.[49] The delithiation of the LiCoO2 cathode was observed by HAADF and ABF after a high voltage biasing, which is an appropriate example for explaining the different features of HAADF and ABF. The pristine single crystal LiCoO2 became nanosized polycrystal after delithiation and figure
 | Fig. 6. (a) HAADF image of delithiated LiCoO2 using the GPA method. (b) and (c) are HAADF and ABF images from the yellow region in (a), and (d) and (e) are HAADF and ABF images from the pink region in (a).[49] |
STEM has a sub-angstrom resolution, which can directly reveal significant information on the physical and chemical properties of materials at the atomic level, such as phase transformation, surface/interface structure evolution, microscopic mechanisms of lithium ion diffusion and storage, and so on. Nevertheless, STEM still has some limitations. For example, the strong radiation of STEM can rapidly damage samples and both STEM and TEM images are actually two-dimensional projections of three-dimensional samples, which can be misleading. Therefore, the combination of computation and TEM imaging is very necessary, as the calculation can make up for the shortcomings of TEM imaging. The calculation methods are more applicable and not affected by the radiation damage, regardless of whether the sample is conductive or not. What is more, calculation methods can construct various periodic, even nonperiodic models, such as surface/interface models, which can provide a convenient interpretation of two-dimensional TEM images. Based on this, Yue et al. provided further insight on the intercalation/deintercalation process of Li and Na ions into Fe2(MoO4)3 combining the first-principle thermodynamic calculations and direct atomic-scale observation by STEM.[50] With the combination of STEM and calculation, the “discrete occupation” and “pseudo-continuous” were proposed to describe the distinctly different occupation paths of Li and Na ions into Fe2(MoO4)3.
Different from real space information, the energy state of an atom or a molecule can experience energy level transition when it undergoes external stimulation such as x-ray irradiation or electron impact. The energy level information is strongly correlated with electronic structure information of the sample which consists of charge, orbital, and even spin information of the elements. In terms of different external stimulation methods, researchers have developed x-ray energy-dispersive spectroscopy (XEDS), EELS, which are generated from the interaction of electrons and sample, x-ray absorption spectroscopy (XAS), x-ray photoelectron spectroscopy (XPS), which rely on the x-ray sources.
XEDS is a widespread option for SEM and TEM at present and it is easy to use for distinguishing various elements. In an electron microscope, a high-energy electron beam penetrates outer-shell electron cloud and interacts with inner-shell electrons so that the inner-shell electrons are ejected. Subsequently, the outer-shell electrons fill the empty energy level and emit characteristic x-rays. If the incident electrons penetrate through the electron shells and directly interact with nuclei, the electrons will decelerate and emit continuous x-rays that are called bremsstrahlung x-rays which need to be filtered in the spectroscopy analysis.[51] In short, XEDS collects the signal of x-rays while differentiates diverse elements by characteristic x-rays. The application of XEDS mapping has become a feasible and effective way to discover elements’ distribution in real space for energy materials.[52,53]
In TEM, EELS collects transmission electrons and analyzes their energy distribution. Inelastic transmission electrons also contain electronic structure information inside the loss of energy. Comparing with XEDS, EELS can detect and quantify all the elements, meanwhile offers atomic level spatial resolution and valence state level energy resolution. Gong et al. studied the delithiation of LiNi0.5Mn1.5O4 cathode from various zone axes in atomic scale.[54] HAADF image of antiphase boundaries from ⟨ 112 ⟩ zone axe is shown in Fig.
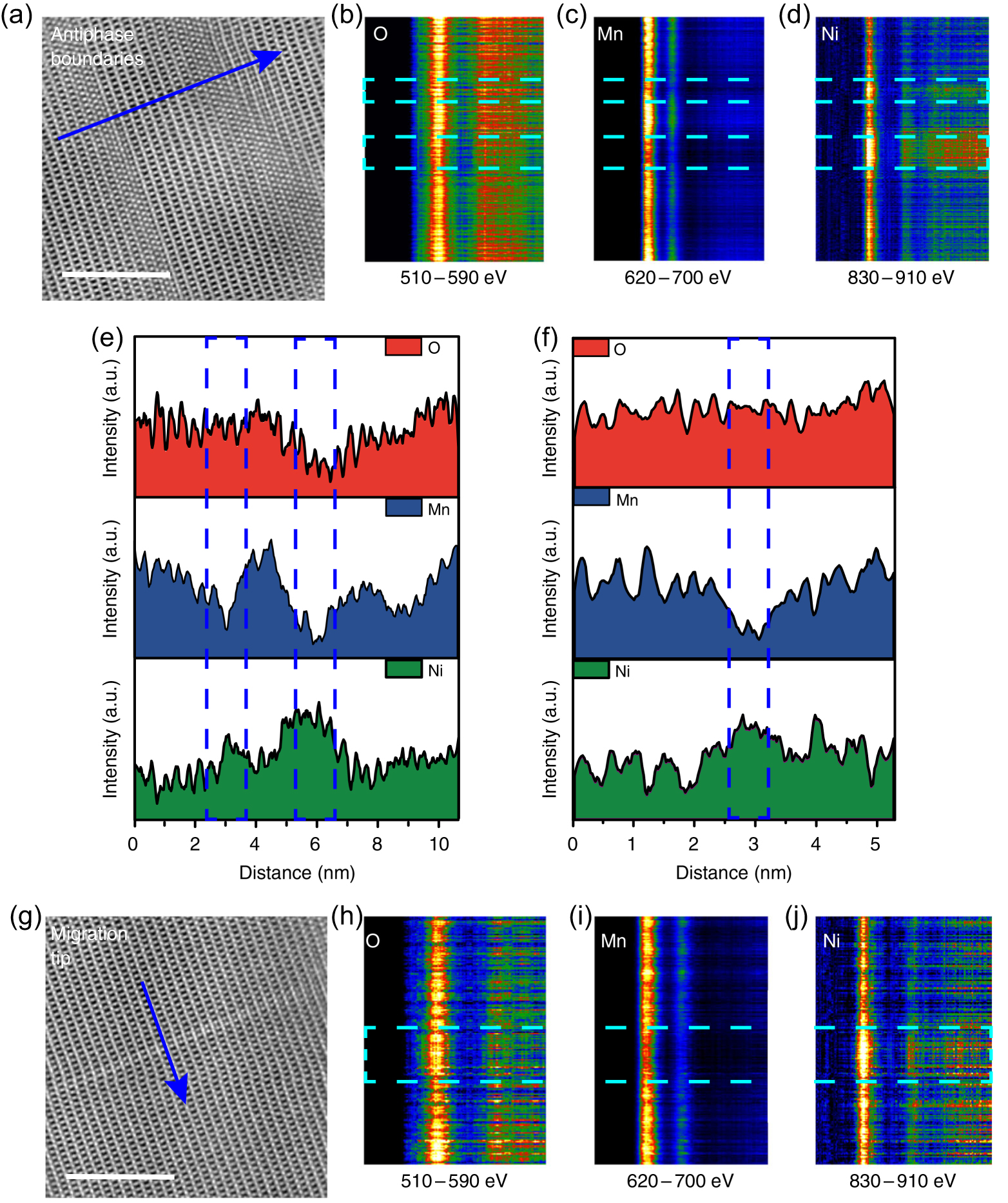 | Fig. 7. (a) HAADF image of antiphase boundaries with blue arrow showing the EELS line scan trajectory. (b)–(d) EELS spectra of O, Mn, and Ni. The dashed rectangle represents two antiphase boundaries in (a). Elements content distribution results of EELS from antiphase boundaries region (e) and migration front region (f). (g) HAADF image of migration front area with blue arrow showing the EELS line scan trajectory. (h)–(j) EELS spectra of O, Mn, and Ni. The dashed rectangle represents migration front in (g). Scale bar, 5 nm.[54] |
With tuning the photon energy to excited electron energy, XAS can obtain electronic structure by energy level transition. A typical x-ray absorption spectrum comprises x-ray absorption near-edge structure (XANES) and extended x-ray absorption fine structure (EXAFS). XANES is sensitive to valence state and coordination of elements and EXAFS is good for quantifying local structural information.[4] Su’s group traced the valence state of Fe in spinel Fe3O4 cathode to investigate the cause of capacity fading via synchrotron XAS.[55] XANES of Fe K-edge of different cycled Fe3O4 cathode is shown in Fig.
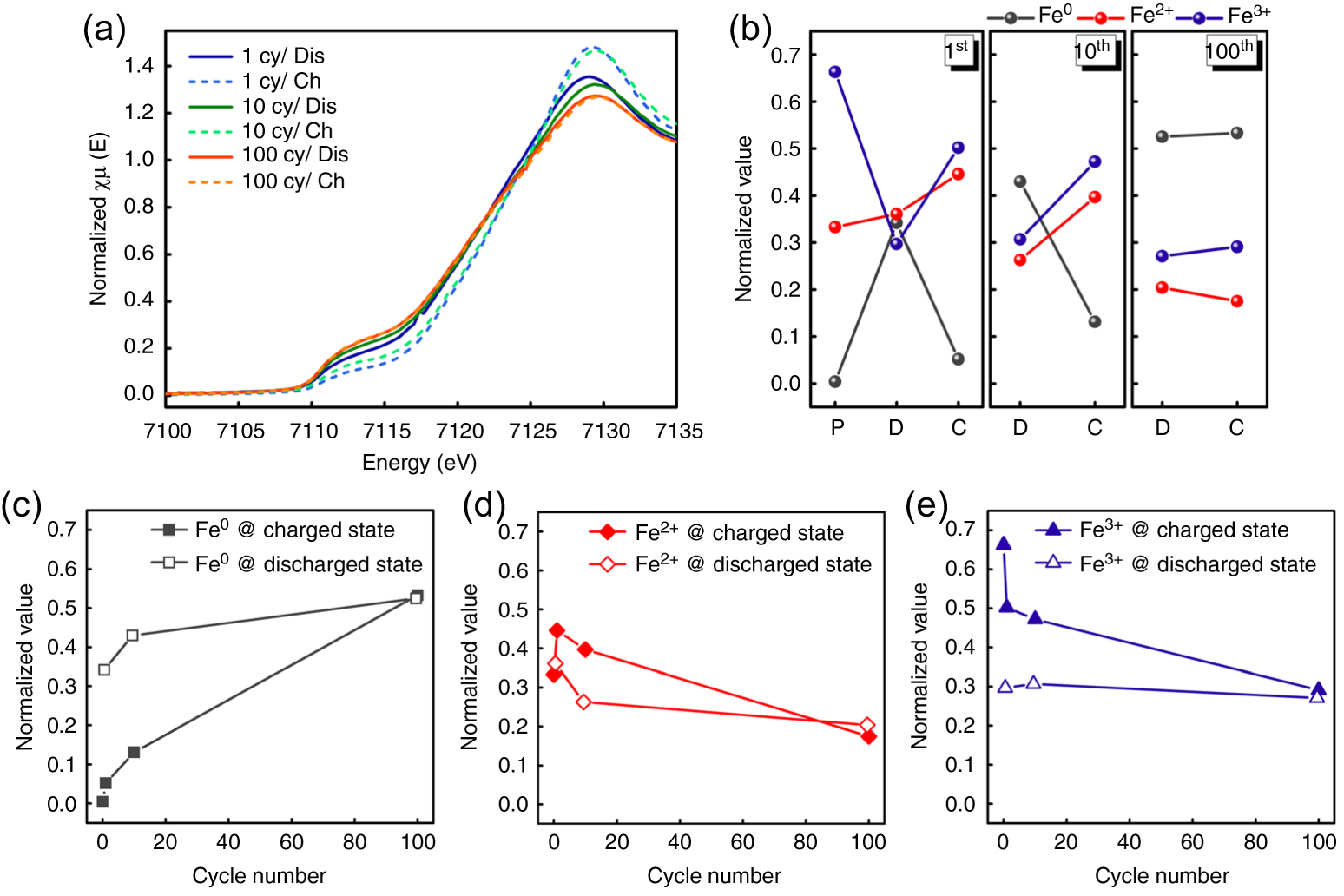 | Fig. 8. (a) XANES spectra of electrode materials at discharge and charge states of different cycles. (b) Quantification of the oxidation states of Fe for different cycles. Pristine, discharged, and charged are represented with P, D, and C, respectively. (c)–(e) Quantification of the oxidation states of Fe as a function of cycle number.[55] |
In the domain of surface analysis, XPS exploits core-level photoemission to probe the valence state and the element composition of samples. Although the sensitivity of XPS is no match for XAS, the direct relationship between photoelectron and energy level makes XPS a great technique in extracting chemical information from sharp core-level peaks from the same elements.[56] Nowadays, a great many interfaces and protected layers studies have employed XPS for in situ or ex situ observing the surface information of various batteries.[57,58]
Compared to characterization tools, the energy scale calculations can predict the stability, defect formation energy, and ion transport mechanism of electrode materials. The stability of cathode material is very important for LIB, as cathode material is still the lithium source of the battery currently. If the cathode is not stable in the electrochemical reaction processes, the side reactions will lead to the rapid decay of battery performance, and even bring safety risks. Wang et al. presented a new method based on the first-principles approach for predicting the thermodynamics of thermal degradation of charged cathode materials for LIB.[59] The calculated decomposition heat for three systems is in good agreement with experiments on three cathode materials: LixNiO2, LixCoO2, and LixMn2O4. Gao et al. used first-principles calculations within the Perdew–Burke–Ernzerhof exchange–correlation functional and the Hubbard-type correction U (PBE +U) scheme to show that Mo doping is beneficial for improving both the dynamic and thermodynamic properties of Li2MnO3.[60] Figure
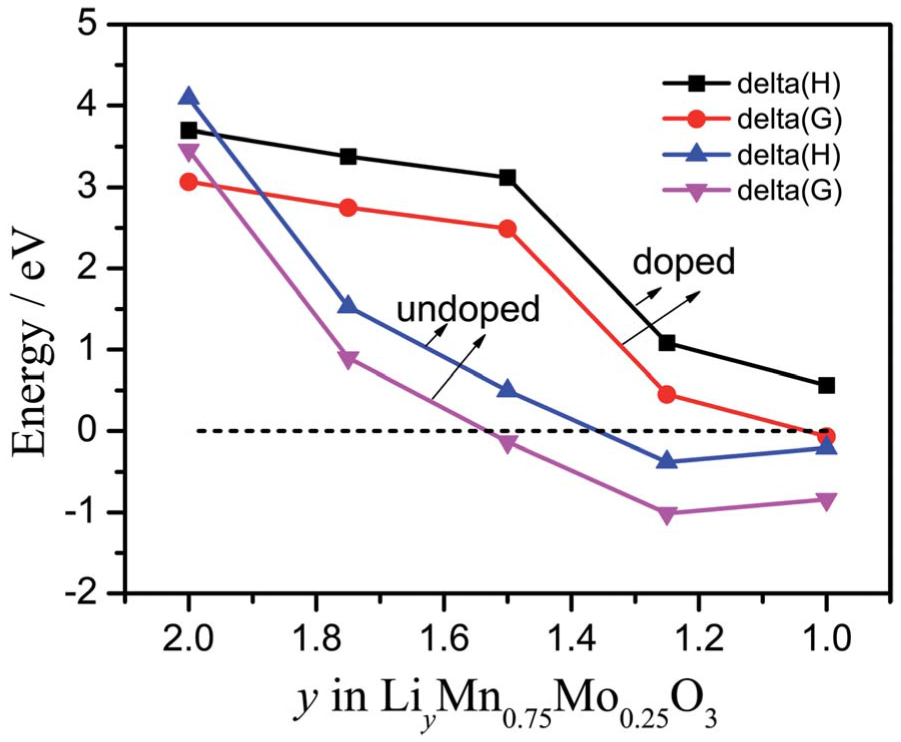 | Fig. 9. Calculated reaction enthalpy and Gibbs free energy for O2 release from different delithiation states LiyMnO3 and LiyMn0.75Mo0.25O3, where y = 2, 1.75, 1.5, 1.25, and 1, for Li2MnO3 and Li2Mn0.75Mo0.25O3, respectively.[60] |
Defects and impurities in materials can also change many properties of materials, including the electronic conductance and ionic conductance. Hoang et al.[61] reported a first-principles study of various monovalent elements doped into different lattice positions of LiFePO4.[61] They found that it is possible to effectively enhance the electronic conductivity of LiFePO4 through defect control. The path and energy barrier of Li+ transportation are directly related to the rate performance and polarization of batteries. Ouyang et al. used the adiabatic trajectory method to obtain the migration energy barriers for the migration of Li ions and Cr ions along the one-dimensional diffusion pathway in pure and Cr doped LiFePO4 from first-principles calculations.[62] The results showed that while Li ions can diffuse along the diffusion pathway easily, Cr ions do not easily diffuse away from their initial positions. This means that the heavy Cr ions will block the one-dimensional diffusion pathway of the material. Yang et al. investigated the mechanisms for thermal self-diffusion of Li ions in fully lithiated LiFePO4 with spin polarized ab initio molecular dynamics calculations.[63] It was found that Li ion diffusion is not a continuous process but through a series of jumps from one site to another.
The physical quantities that depend on momentum space such as lattice vibration and energy band determine the thermal, mechanical, electrical, and many other properties of materials. However, the methods of momentum characterization in the field of rechargeable batteries still scarcely attach importance to the dispersion in momentum space because of the complexity of the battery system. In this section, we will focus on phonon dispersion and energy band structure of battery-related materials.
The energy of a phonon mode is on the order of 10–102 meV, therefore an energy transfer around vibration energy must be achieved to characterize the vibrational modes of materials. At present, many different techniques have successfully probed the phonon dispersion. Inelastic scattering techniques including inelastic x-ray scattering[64,65] and inelastic neutron scattering[66,67] are old-style methods, but they are rarely used in battery research. Optical spectroscopy exploits the inelastic scattering of photons to detect the vibrational modes, for example, Raman spectroscopy, which has been widely applied for detecting the structural variations of battery materials.[68] Zaghib et al. used in situ Raman spectroscopy to investigate the vibrational modes in Cr/Co-doped LiMn1.5Ni0.5O4 cathode and study the valence state change of Ni and Mn in real time.[69]
Two-dimension materials are of great importance in the field of rechargeable batteries. Recently, Kazu et al. reported a novel method to simultaneously map the vibration in graphene nanostructures in real space and momentum space.[70] Different from low-spatial-resolution inelastic x-ray (neutron) scattering techniques and low-momentum-transfer optical spectroscopy, EELS in transmission can provide local vibrational modes of two-dimension monolayer materials for several Brillouin zones at the nanometer scale. There must be a tradeoff between spatial resolution and momentum resolution because of the uncertainty principle. With the energy resolution of 30 meV full width at half maximum (FWHM), the momentum resolution of ± 0.1–0.2 Å−1, and the probe size of 10–40 nm, phonon dispersions along different momentum space directions are measured and they are perfectly accord with simulated results. Except for the missing of the low-energy region, details of the phonon dispersions are mostly described.
Yao et al. used first-principles density functional theory (DFT) calculations to investigate both the disordered rock salt-type Li4Mn2O5 structure and the ordered ground-state structure.[71] From Fig.
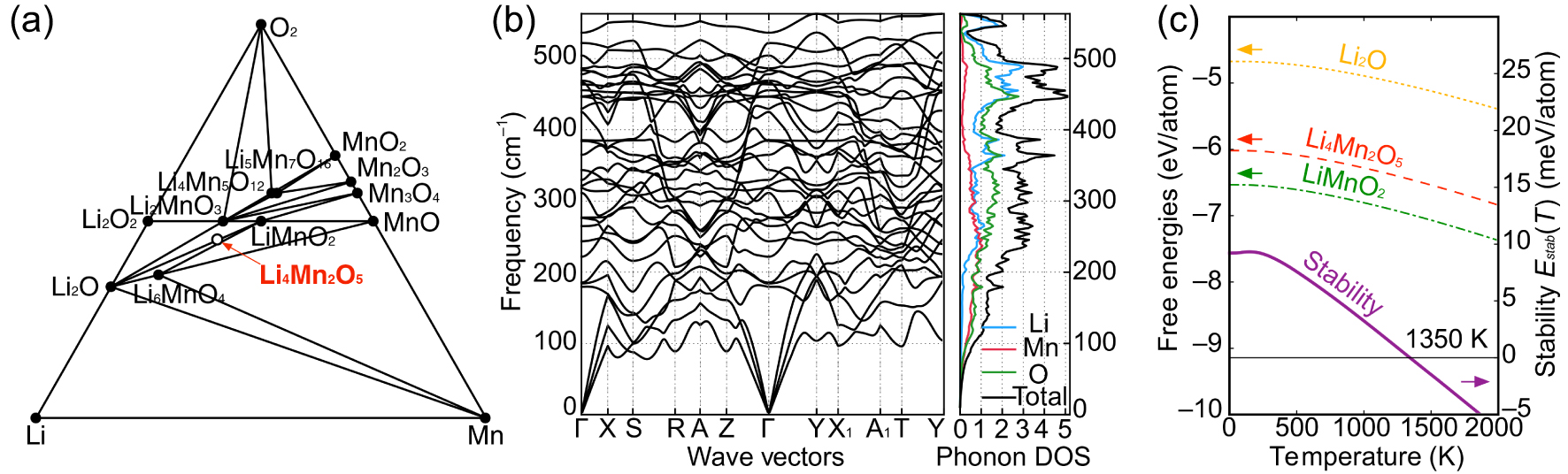 | Fig. 10. Thermodynamic and dynamic stabilities of Li4Mn2O5. (a) Calculated Li–Mn–O (T = 0 K) phase diagram. The Li4Mn2O5 phase is slightly higher in energy (13.6 meV per atom) relative to the ground-state phase: a mixture of Li2O and LiMnO2. (b) Phonon dispersion of the ground-state Li4Mn2O5 and (c) calculated temperature-dependent free energy of Li4Mn2O5 (red dashed line), Li2O (orange dotted line), and LiMnO2 (green dotted line), as well as the stability (purple solid line) of Li4Mn2O5 versus temperature relative to Li2O and LiMnO2 phase mixtures. Li4Mn2O5 is dynamically stable and can be entropically stabilized at ∼ 1350 K.[71] |
The electronic energy band of solid materials is very important for battery design, for it describes the quantum-mechanic-allowable electron energy state which strongly influences the electrical property of electrodes and solid-state electrolytes. The electronic structure of the battery material is closely related to their electrochemical properties, for example, the chemical stability of the interface between the electrode and the electrolyte can be derived from the density of energy states,[72] the rate performance is related to the electronic conductivity of the electrodes,[73] solid electrolyte materials require electronic insulation properties, which are related to the width of the energy gap.[74]
Nevertheless, experimental characterization of the energy band is still limited to a few techniques such as angle-resolved photoemission spectroscopy (ARPES) and resonance Raman spectroscopy (RRS). ARPES directly observes the distribution of electrons in momentum space by photoemission electrons and it has become one of the most indispensable techniques for characterizing the physical property.[75] Usachov et al. employed ARPES to study the energy band of N-doped graphene.[76] The nitrogen impurities could tune the band structure and carrier concentration of N-doped graphene for optimizing the performance of energy devices.
If the energy of the incoming or outgoing photon matches the electronic transition energy of the sample, the Raman cross section will notably increase, which is called RRS.[77,78] As a result, RRS relates the Raman signals to the electronic energy band. Today, the energy band structure of many types of materials has been studied by RRS.[79,80] These kinds of momentum-related characterizations in the momentum space enlighten the followers to discover the quality of battery materials from a brand-new angle.
The calculation of energy band is scarce in the field of rechargeable batteries none the less. Chen et al. demonstrated that carbon foams (CFs) exhibit good stabilities and pore-size dependent electronic properties, which are related to the size-dependent band gaps of graphene nanoribbons (GNRs) through first-principles calculations.[81] Then they used 48Z_SI as an example to calculate the band structures of monolayer graphene nanoribbons-based asymmetric zigzag CFs to find out the rules (Fig.
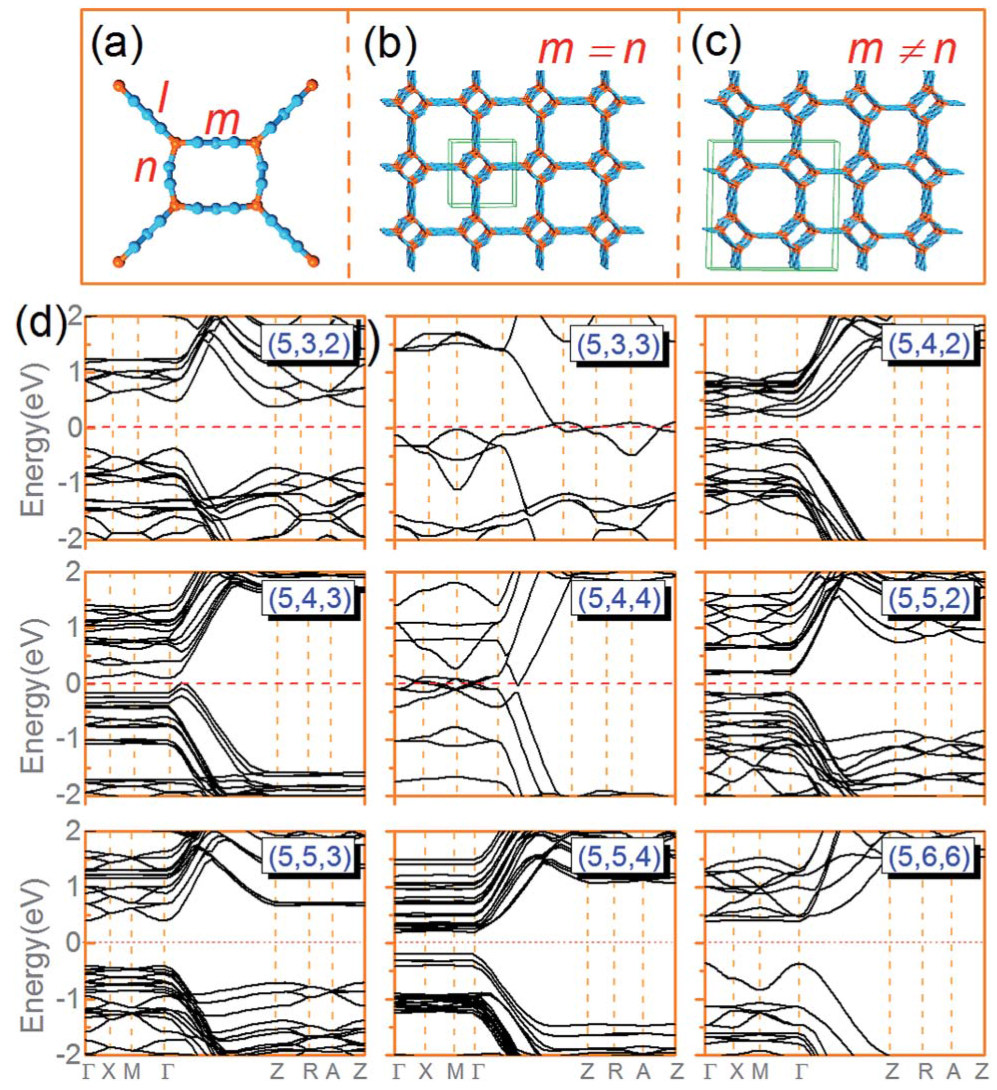 | Fig. 11. The schematics of asymmetric 48Z_SI(l, m, n) networks and the corresponding band structures. (a) Three-wing GNRs building block of asymmetric CFs and three width degrees of freedom, l, m, n, are considered. (b) and (c) m = n and m ≠ n asymmetric CFs, respectively. The orange and cyan sticks indicate the sp3 and sp2 C atoms, respectively. (d) The band structures of (5, 3, 2), (5, 3, 3), (5, 4, 2), (5, 4, 3), (5, 4, 4), (5, 5, 2), (5, 5, 3), (5, 5, 4), and (5, 6, 6).[81] |
On account of the demand for higher time resolution, especially for ultrafast charge and discharge of batteries and in situ experiments, the time-resolved characterization tools are critical for ultrafast dynamic processes. Unlike picosecond in the field of solar cell,[83] the time-resolved characterizations always focus on the magnitude of second referring to rechargeable batteries, such as time-resolved XRD, XAS, and in situ TEM, because of the sluggish dynamic reaction in electrode and electrolyte scale. However, the dynamics of atomic scale processes in millisecond and even picosecond scale are rarely studied at present.
In situ TEM directly observes the real-time evolution of electrode that is feasible to acquire the mechanism of reactions in batteries. The first research of lithiation evolution by Huang et al. reached a time resolution of a half second for the morphology evolution of the SnO2 anode in 2010.[84] Lately, He et al. studied the lithiation of SnSe2 by in situ HRTEM with a similar time resolution but a higher spatial resolution to clearly observe the lattice fringes of SnSe2.[85] It is obvious that a tradeoff restricts the spatial resolution and the time resolution. Atomic spatial resolution and better time resolution are still needed to achieve for studying the microscopic mechanism of the battery system. The x-rays related tools also demand higher time resolution for detecting the processes of the crystal structure evolution and valence state evolution.[86] Yang et al. used in situ XRD and XAS to characterize the structural and valent changes of LiNi1/3Mn1/3Co1/3O2 cathode at different charge rates.[87] The time resolution of XRD and XAS is also on the order of several seconds. In general, the time resolution of characterization tools in the research of batteries is around several seconds nowadays and it is enough for observing the macroscopic phenomenon. But for microscopic behaviors, a higher time resolution is still required for investigating in-depth mechanism of the battery system.
As for the computation, Leung et al. used ab initio molecular dynamics (AIMD) simulations to study ethylene carbonate (EC) decomposition process in the electron-rich anode regions in real-time. With an explicit treatment of the EC liquid environment, an excess electron can induce EC decomposition within AIMD timescales. Both CE–O1 and CC–O1 cleavages occur, yielding 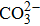
Advanced characterization and calculation methods provide an opportunity to investigate the structure–activity relationship of rechargeable battery materials comprehensively. From four different scales, the structure and electronic structure can be generally described. In this review, we have introduced the most representative characterization and calculation tools that have been used in battery systems from the scales of real space, energy, momentum space, and time. Overall, present studies in the field of rechargeable batteries focus on the information of real space structure and energy level transition processes, nevertheless, it is scarce to study the material properties in momentum space and ultrafast time scale (namely, millisecond or less). In addition, the combined analysis of different scales is useful but scarcely reported for battery studies. Therefore, some potential directions for future development of characterization and calculation methods are discussed below.
Analysis combining multiple scales is the first direct choice to achieve a multi-dimension assessment of battery material properties. For example, simultaneous analysis of STEM image and EELS, even employing the time-resolved TEM technique, can draw a picture including the real space, energy level transition, and ultrafast dynamic information, which is able to boost the investigation of battery reaction mechanisms. Besides, the development of in situ or operando techniques has brought a direct time-resolved method to observe the dynamic evolution of energy materials, especially for high-rate discharge/charge processes. However, the time resolution of the present in situ technique is mostly confined to sub-second scope in the field of rechargeable batteries. Better time resolution such as sub-millisecond is badly needed to detect the phase transition or some other rapid processes in the nonequilibrium system of reacting batteries and further improved computing power can simulate more complicated and rapid processes. Learning from some up-to-date research,[89] machine learning is suited for us to find some significant materials rather than repetitive work which wastes a large amount of time. Finally, pretty few reports about momentum dispersion of phonons or electrons are published, which probably suggests that the energy band structure and vibration modes of materials are still not rigorously studied in the field of rechargeable batteries.
To date, the characterization and calculation methods for rechargeable batteries are extensive developed, but problems of each method still limit the applications, such as limited resolution and poor computational efficiency. However, with the combination of multiple scales analysis, a fairly good description of material structure and electronic structure could be realized for investigating the structure–activity relationship of energy materials or other functional materials and designing desirable materials with better performance.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] | |
| [39] | |
| [40] | |
| [41] | |
| [42] | |
| [43] | |
| [44] | |
| [45] | |
| [46] | |
| [47] | |
| [48] | |
| [49] | |
| [50] | |
| [51] | |
| [52] | |
| [53] | |
| [54] | |
| [55] | |
| [56] | |
| [57] | |
| [58] | |
| [59] | |
| [60] | |
| [61] | |
| [62] | |
| [63] | |
| [64] | |
| [65] | |
| [66] | |
| [67] | |
| [68] | |
| [69] | |
| [70] | |
| [71] | |
| [72] | |
| [73] | |
| [74] | |
| [75] | |
| [76] | |
| [77] | |
| [78] | |
| [79] | |
| [80] | |
| [81] | |
| [82] | |
| [83] | |
| [84] | |
| [85] | |
| [86] | |
| [87] | |
| [88] | |
| [89] |

