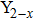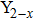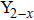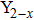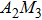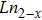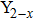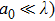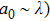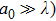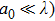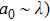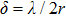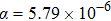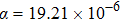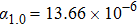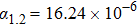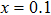Cite this Article
Liu Xian-Sheng, Cheng Yong-Guang, Yuan Bao-He, Liang Er-Jun, Zhang Wei-Feng. Laser scattering, transmittance and low thermal expansion behaviors in Y 2 − x (ZnLi)xMo3O12 by forming regular grains. Chinese Physics B, 2019, 28(9): 096501  
Permissions
Laser scattering, transmittance and low thermal expansion behaviors in Y 2 − x (ZnLi)xMo3O12 by forming regular grains
Liu Xian-Sheng1, Cheng Yong-Guang2, Yuan Bao-He3, Liang Er-Jun4, †, Zhang Wei-Feng1, ‡
Henan Key Laboratory of Photovoltaic Materials and Low Dimensional Materials Science Laboratory, Henan University, Kaifeng 475004, China
College of Science, Center of Analysis and Testing of Henan Institute of Engineering, Zhengzhou 451191, China
North China University of Water Resources and Electric Power, Zhengzhou 450011, China
School of Physical Science & Engineering and Key Laboratory of Materials Physics of Ministry of Education of China, Zhengzhou University, Zhengzhou 450052, China

 

† Corresponding author. E-mail: ejliang@zzu.edu.cn wfzhang@henu.edu.cn

Abstract

Ceramics usually have irregular grains, cracking, or porosity, which result in their lightproof. Y2Mo3O12 ceramics have more porosity due to the heavy hygroscopicity. Introducing ZnLi to Y2Mo3O12 could form regular grains, reduce cracking and porosity. With increasing the content of ZnLi, the grain shapes self-assembly gradually and then the laser scattering and transmittance improve. The laser scattering property and transmittance of diverging rays become the best in ceramics (ZnLi)xMo3O12 (x=1.0 and 1.2) with regular grains and low thermal expansion. The formation mechanism of regular grains is ascribed to the substitutions of Zn2+ and Li+ for Y3+ in Y2Mo3O12 resulting in the preferential growth. The investigation in laser scattering, transmittance and low thermal expansion behaviors of (ZnLi)xMo3O12 could pave a way to weaken the strong-laser attack from the high-power laser weapon and the other.

PACS: 65.40.De;78.20.Ek;81.05.Je;81.10.Jt
Keyword:low thermal expansion;laser scattering;regular grains;diverging rays transmittance
1. Introduction

The harm on the aircrafts from a strong laser weapon is mortal although the strong laser undergoes the atmosphere refraction, absorption, scattering, turbulence, thermal blooming, and breakdown.[1–3] Scattering the laser beam to diverging rays with high transmittance rate by a protective layer on aircrafts is the optimal method to weaken the mortal attack from the high-power laser weapon. However, the protective layer could fall off due to thermal expansion on heating from laser. Negative thermal expansion (NTE) materials could find applications due to their abnormal thermal expansion properties and potential applications in realizing near-zero thermal expansion.[4–7] NTE mechanisms such as phonon anharmonicity, phase transition, charge transfer, Jahn–Teller effect, and nanoscale effect have been proposed to explain the NTE origin successfully for open framework structure materials, magnetic and ferroelectric materials, high pressure-phase LaCu3Fe4O12 and BiNiO3, etc.[4–18] Of the NTE materials, the 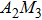O12 (A: trivalent ion, M: W or Mo) family with larger NTE coefficients and stable open framework structure is very attractive, however the heavy hygroscopicity resulting in the disappearance of NTE near room temperature and the single function are the main obstacle for its applications to reduce the thermal expansion coefficient.[19–28] During the release process of crystal water, A2Mo3O12 even shows an abrupt positive thermal expansion, and only after the complete release of crystal water, the NTE presents. To reduce the hygroscopicity of A2Mo3O12, some trivalent ions have been employed separately to substitute the A 3+ ions, such as Al3+, Fe3+, Cr3+, La3+, Ce3+: Yb2−xAlxMo3O12, Fe2−xYxMo3O12, 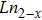CrxMo3O12 (Ln: Er, Y), Y2−xLaxMo3O12, Ce3+/Y2Mo3O12.[20–24] Partial uni-ion substitution for A 3+ changes the large openings in the network[21] and the bond angle of A–O–M, therefore, the hygroscopicity of A2M3O12 is reduced greatly. The primary orthorhombic structure of Y2Mo3O12 changes in space group (Pba2 to Pbcn[29]), and even transforms to monoclinic[20,21,28] or tetragonal structures.

The above investigations suggest that it may be difficult to retain the orthorhombic structure after eliminating the hygroscopicity of Y2Mo3O12 by the partial uni-ion substitution for Y3+. The reason is ascribed to the different structures of monoclinic (A 3+ with smaller radius) or tetragonal (A 3+ with much larger radius) with orthorhombic (A–Y, Yb). Considering the orthorhombic structure of Li2Mg2Mo3O12,[30] in our recent investigation, two ions of Li+ and Mg2+ have been adopted as the substitution ions for Y3+ and then the hygroscopicity of Y2Mo3O12 was reduced.[31] However, detailed investigation suggested that even though remaining the orthorhombic structure, the x-ray diffraction (XRD) peaks changed so much that some orientations such as (102) and (131) were separate from the others due to the large radius difference between Li+ (76 pm) and Mg2+ (72 pm), consequently, the grain clearance was observed obviously. The result indicates that two ions with less radius difference should be under consideration to change the crystal structure moderately, so that the hygroscopicity and grain clearance are reduced together and multi-function could be realized.

In the present paper, considering the orthorhombic structure of Li2Zn2Mo3O12,[32,33] Li+ (76 pm) and Zn2+ (74 pm) with less radius difference as substitutions for Y3+ are adopted to reduce the hygroscopicity and obtain regular grains. The orthorhombic structure changes gradually and the hygroscopicity decreases with increasing the content of (LiZn)3+. The low thermal expansion ceramics Y2−x(ZnLi)xMo3O12 (x=1.0 and 1.2) with regular grains possess excellent laser scattering property and high transmittance rate of diverging rays. The relationship between the laser scattering property/transmittance and regular grain is discussed.

2. Experiment

Analytical regents of Y2O3, MoO3, ZnO, and LiNO3 as raw materials were weighted according to the stoichiometric ratios of destination materials of Y2−x(ZnLi)xMo3O12 (x = 0, 0.1, 0.3, 0.5, 0.7, 0.9, 1.0, 1.2, 1.4, 1.6, 1.8, 2.0). The raw materials were mixed and ground for about 2 h. The mixtures were coldly pressed into pellets at pressure about 200 MPa followed by sintering at 1073 K for 5 h in air and then cooling down to room temperature naturally.

XRD measurements were carried out with a Bruker D8 Advance x-ray diffractometer to analyze the crystal structure. Raman spectra were recorded with a Renishaw inVia Raman spectrometer with 633 nm laser excitation. The microstructures and energy dispersive spectra of the samples were examined with a scanning electron microscopy (SEM, Model Quanta 250). The thermogravimetry (TG) and differential scanning calorimeter (DSC) measurements were carried out on a Netzsch STA 449F3 simultaneous thermal analyzer in the temperature range of 300–700 K, with the heating rates of 10 K/min. The linear coefficients of thermal expansion (CTE) were measured with a dilatometer (Linseis DIL L76). The laser with wavelength of 633 nm and power of about 50 mW passed through a microscope objective lens connecting with the Raman spectrometer. The laser is a He–Ne laser with the brand of Renishaw. The red laser (633 nm) scattering pictures were recorded with a digital camera (Canon 100D).

3. Results and discussion
3.1. Laser scattering property and regular grains formation of 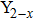(ZnLi)xMo3O12

Figures 1(a)–1(e) show the red laser (633 nm) scattering pictures of Y2−x(LiZn)xMo3O12 with x=0.3, 0.7, 1.0, 1.2, and 1.8. For the ceramic sample with x=0.3 (Fig. 1(a)), when a laser beam (633 nm) illuminates the surface of the ceramic block, the laser beam is scattered and half of the ceramic block becomes bright because some diverging rays are transmitted. The bright field is larger than half of the ceramic block for the ceramic sample with x=0.7 (Fig. 1(b)). Especially, for the ceramic samples with x=1.0 and 1.2, the whole ceramic blocks are bright and much more diverging rays are transmitted (Figs. 1(c) and 1(d)). However, only much size is bright for the ceramic sample with x=1.8 (Fig. 1(e)).

Fig. 1. (a)–(e) Red laser scattering and transmittance pictures of Y2−x(LiZn)xMo3O12 with x=0.3, 0.7, 1.0, 1.2, and 1.8. The laser beam is focused on the upper surface center of the pellets. The diameters of the pellets are about 0.8 cm. The heights of the pellets are about (a) 5 mm, (b) 5 mm, (c) 6 mm, (d) 5 mm, and (e) 6 mm. (f) Schematic diagram of laser scattering and transmittance in the ceramic grains.

The laser scattering is reported to relate to the size of the ceramic particles.[34] In general, when a laser beam illuminates the surface of a ceramic, the laser beam will be absorbed and scattered partly. Laser scattering could be divided into three types: Rayleigh ( 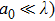, Mie ( 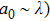, and Tyndall ( 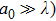, where a0 is the size of the scattering center and λ is the laser wavelength. For Rayleigh ( 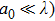and Mie ( 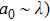scatterings, the scattering cross section relates to 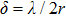. The scattering coefficient increases with the size of the scattering microspheres when the sphere diameter is smaller than the wavelength and reaches the maximum when the particle size equals to the laser wavelength, and thereafter decreases with the particle size.

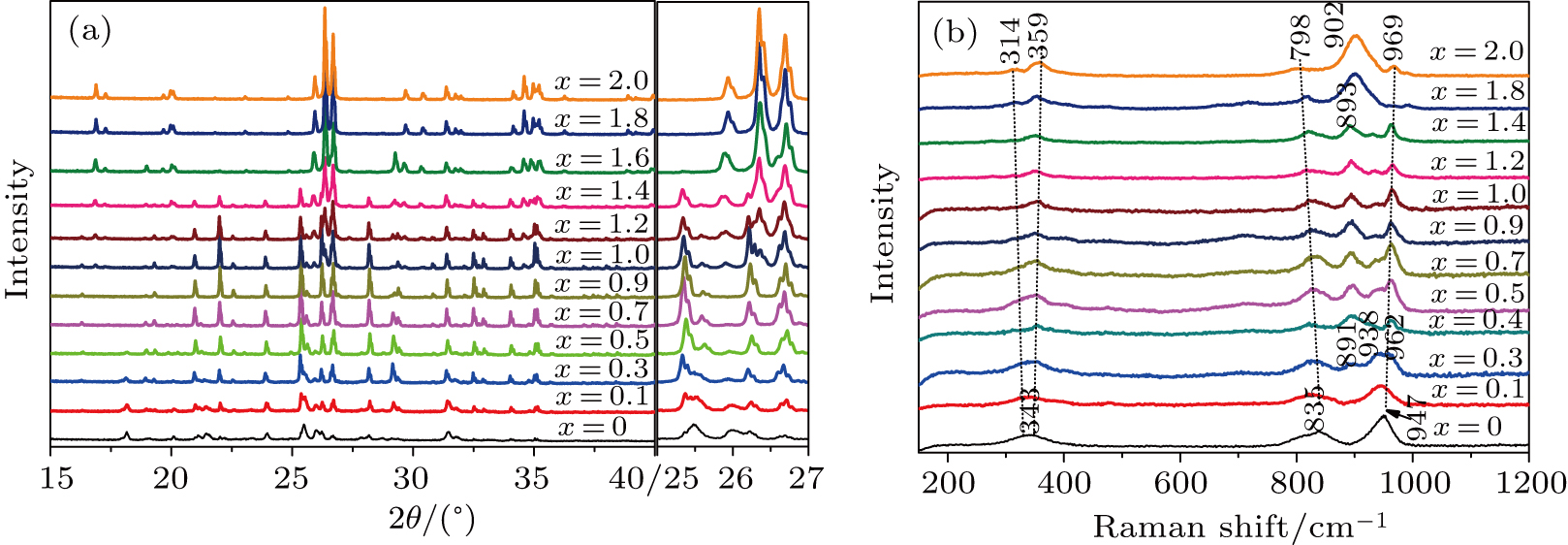
In order to explore the effects of the grain size and pores on the laser scattering phenomenon, the microstructure of Y2−x(LiZn)xMo3O12 was investigated with SEM. Figure 2 shows the SEM images of Y2−x(LiZn)xMo3O12 with different contents of (LiZn)3+. For pure Y2Mo3O12 (Fig. 2(a)), squeezed together spherical grains are separated with each others by some pores due to the influence of crystal water and air left in the ceramics. For x=0.3 (Fig. 2(b)), even though with less content of (LiZn)3+ in Y2Mo3O12, the air pores in the ceramics are reduced largely and much larger spherical grains appear. When the content reaches x=0.7 (Fig. 2(c)), the regular quadrangular prisms and tetrahedral are observed, i.e., the grains appear edges and corners rather than mere circular arcs, however, air pores still exist. For x=1.0 (Fig. 2(d)), larger regular grains contact with each other along straight edges and some smaller grains fill in the clearance among particles, therefore, there are much less pores. Then there appear some octahedra, rods among the grains with straight edges (see image of the sample with x=1.2 in Fig. 2(e)), which grow along the slits among the larger grains.

Fig. 2. (a)–(h) SEM images of Y2−x(LiZn)xMo3O12 with x = 0, 0.3, 0.7, 1.0, 1.2, 1.4, 1.6, 1.8, and 2.0. The grain shapes change remarkably with increasing the content of (LiZn)3+.

The continuous change in grain shapes rather than the grain sizes is found with increasing the content of (LiZn)3+ in Y2Mo3O12. The results suggest that the grain shapes in Y2−x(LiZn)xMo3O12 ceramics could change the laser scattering behavior. The transmittance of diverging rays could also be related to the regular grains and density of the ceramics. The regular grains have less porosity and high density.

The octahedra and rods have more content of (LiZn)3+ in Y2Mo3O12 and the larger grains with straight edges have lower content of (LiZn)3+, which can be discerned from the relative intensities of the peaks of Zn, Y, Mo in the EDS spectra (see Figs. 3(a)–3(e)). For x=1.4 (Fig. 2(f)), the amount of (LiZn)3+ takes up the majority in Y2−x(LiZn)xMo3O12, i.e., Y3+ as a substitution ion, the tetrahedra are of (LiZn)2Mo3O12 with certain amount of Y3+. The grains grow along the substitution direction to form the rods/point ends according to the lowest energy principle along the substitution direction. However, excess (LiZn)3+ induces some pores even though some small grains fill in the pores (Figs. 2(g) and 2(h)). Therefore, a suitable amount of (LiZn) is critic for high relative density of Y2−x(LiZn)xMo3O12, which results from the filling effect of the small grains. Though the theory densities increase with increasing the substitution of (LiZn)3+ for Y3+ in Y2Mo3O12, the relative density of ceramics Y2−x(LiZn)xMo3O12 increases with increasing x to the maximum of 92.85% (x=1.0) and then decreases (Fig. 3(f)).

Fig. 3. EDS spectra of Y2−x(LiZn)xMo3O12 with (a) x = 0, (b)–(d) 1.2, and (e) 2.0. (f) Theory density and relative density curves of Y2−x(LiZn)xMo3O12 with x= 0.5, 0.7, 0.9, 1.0, 1.2, and 1.8.

The remarkable change in the microstructure of Y2−x(LiZn)xMo3O12 is analyzed from sintering behavior as follow. The raw materials of Y2O3 and MoO3 are compacted in a cylindrical mold via point contact containing air pores under pressure. During the sintering process, atoms (Y, Mo, O) and molecules (Y2O3 and MoO3) rapid scatter and then a chemical conversion (Y2O3+3MoO3 Y2Mo3O12) takes place, changing the shape and position of the particles and internal pores. Consequently, smaller particles with larger total surface area transform to lager particles with less total surface area, which are energetically more favorable than the smaller ones. During the cooling process, Y2Mo3O12 expands and some crystal water invades into the crystal from the microchannels. With introducing ZnO and LiNO3 in the raw materials, Zn2+ and Li+ enter into the lattice and substitute Y3+ in Y2Mo3O12, resulting in the shrinkage of microchannels and thereafter reduction of crystal water and air pores. The destructive effect of crystal water on crystal structure could be weakened and the high-temperature crystal structure remains to room temperature. A reduction of grain-boundary-surface energy ratio could be obtained and consequently the densification increases.[35] On the other hand, the crystal grows rapidly along the direction of substitution of (LiZn)3+ for Y3+ due to the lowest energy principle and cylinder/rod particles appear.

Therefore, for the present case, the regular grains and less porosity together should be responsible for the laser scattering and transmittance of diverging rays. Figure 1(f) shows the schematic diagram of laser beam brightening the ceramic grains. A laser beam is scattered by the regular ceramic grains and weak rays exit from the ceramic surface, therefore, the laser energy is dispersed by the ceramic grains. The scattering property of the ceramics could effectively reduce the killing effect of strong laser, whose high energy focus on the surface might melt the target. If the military aircrafts are coated with the as-prepared ceramic Y2−x(LiZn)xMo3O12 with x= 1.0 and 1.2, the high energy of the strong laser from laser guns could be dispersed to diverging rays by the coating layer and the military aircrafts might be safe.

3.2. Crystal structure

Figure 4(a) shows XRD patterns of Y2−x(LiZn)xMo3O12 with x from 0 to 2.0 at room temperature (the left part presents the diffraction of 2θ from 15° to 40°, while the right part corresponds to 2θ from 25° to 27°). For x = 0, there are only a few broad diffraction peaks due to heavy hygroscopicity,[19] which indicates that the crystal water in the lattice lowers the crystal quality of Y2Mo3O12 to form amorphous structure. Crystal water molecules in the lattice drag Y3+ and nearest oxygen ion[24] distorting the growth along crystal plains, which results in less difference between the crystal plains and broadened diffraction peaks.

Fig. 4. (a) XRD patterns and (b) Raman spectra of Y2−x(LiZn)xMo3O12 with x from 0 to 2.0 at room temperature.

With increasing the content of (LiZn)3+ from x=0.1 to x=0.9, the diffraction peaks become sharp, some new peaks corresponding to Pba2-Y2Mo3O12 appear, and some peaks split. For example, the broad diffraction peak about 25.5° according to Pba2-Y2Mo3O12 splits into two peaks at 25.4° and 25.6° (right in Fig. 4(a)), indicating the quality enhancement of the crystal plains of Y2Mo3O12. It is believed that, with increasing the content of (LiZn)3+, smaller ions of Li+ (76 pm) and Zn2+ (74 pm) partially substitute the larger ion of Y3+ (90 pm) to shrink the microchannels in the lattice of Y2Mo3O12 and induce the growth orientation of Y2Mo3O12 crystal (the relative intensities of diffraction peaks are different from those of Pba2-Y2Mo3O12 at 423 K[29]), which results in the decrease of crystal water. However, the transformation from space group Pba2 to Pbcn[29] during the temperature increasing process is not observed, which suggests the different effects between temperature and ion-substitution on the decrease of crystal water. With increasing temperature, the average kinetic energies of crystal water molecules increase enough and run away from the lattice of Y2Mo3O12. The relative sites of Y3+, Mo6+, and O2− change obviously, which results in the change of symmetry. However, with increasing the content of (LiZn)3+ to substitute Y3+, crystal water molecules are repelled out of the lattice. The lattice changes a little due to the substitution of (LiZn)3+. When the content of (LiZn)3+ reaches x=1.0, the lattice changes enough and there appear some new peaks such as peaks at about 25.9° and 26.3°, which are corresponding to (LiZn)2Mo3O12. From x=1.0 to x=1.4, there are two phases of Pba2-Y2Mo3O12 and (LiZn)2Mo3O12. From x=1.6 to x=2.0, there is only a single phase of (LiZn)2Mo3O12.

Figure 4(b) shows Raman spectra of Y2−x(LiZn)xMo3O12 with x from 0 to 2.0 at room temperature. For pure Y2Mo3O12, there are only broad peaks at about 343 cm−1, 835 cm−1, and 947 cm−1 due to the effect of crystal water on the vibrations, which are assigned to symmetric and asymmetric bending motions in both YO6 octahedra and MoO4 tetrahedra, symmetric and asymmetric stretching vibrations of the MoO4 tetrahedra.[15,19,21] With increasing the content of (LiZn)3+, the vibrations of Y–O and Mo–O are affected so strongly that the Raman peaks become sharp and the peaks split: the peak at 343 cm−1 splits into 314 cm−1 and 359 cm−1 and the peak at 947 cm−1 splits into 895 cm−1, 938 cm−1, and 951 cm−1. Even though the peak splitting appears, there is no characteristic peak showing the monoclinic structure.[20,21] The result indicates that the crystal phase is still orthorhombic.

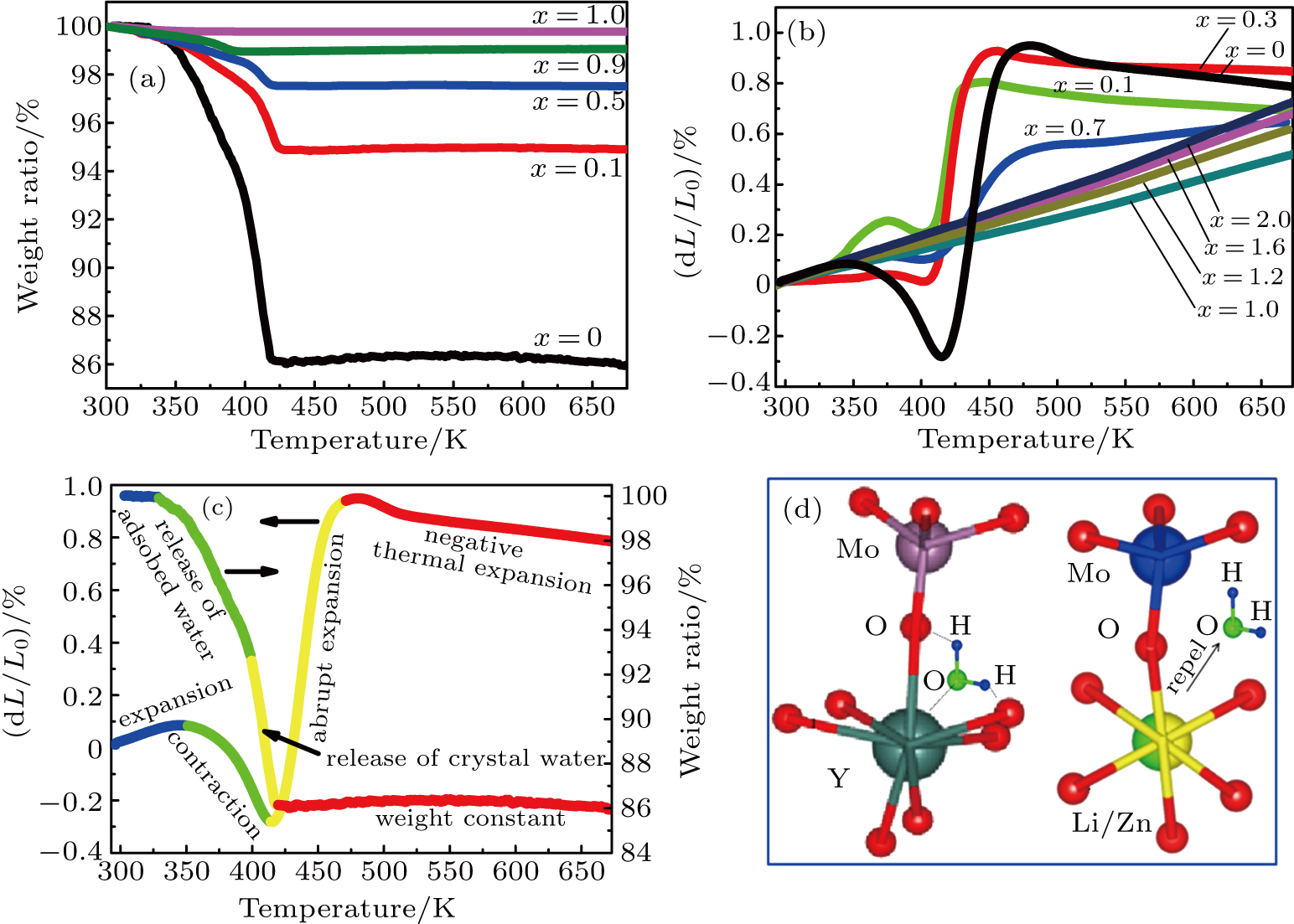
3.3. Hygroscopicity reduction and low thermal expansion property

In order to show the hygroscopicity reduction of Y2Mo3O12 with increasing content of (LiZn)3+, the TG measurements of Y2−x(LiZn)xMo3O12 were performed (see Fig. 5(a)). The amount of crystal water in the samples with different contents of (LiZn)3+ can be estimated with TG curves: Y2Mo3O12 2.97 H2O, Y1.9(LiZn)0.1Mo3O12 0.84 H2O, Y1.5(LiZn)0.5Mo3O12 0.38 H2O, Y1.1(LiZn)0.9Mo3O12 0.18 H2O. The results confirm that the substitutions of (LiZn)3+ decrease the hygroscopicity obviously. The samples (x=1.0 and 1.2) with highest transmission rate of diverging rays have no hygroscopicity. This suggests that the laser scattering and transmittance of diverging rays could also be influenced by crystal water, which is consisted with the result from Fig. 1.

Fig. 5. (a) The TG curves and (b) relative length changes of Y2−x(LiZn)xMo3O12 with different contents of (LiZn). (c) Different effects of absorbed water and crystal water release on the thermal expansion property of Y2Mo3O12: left axis presents the relative length change of Y2Mo3O12; right axis presents the TG of Y2Mo3O12. (d) Schematic diagram of the effect of (LiZn) substitutions on crystal water.

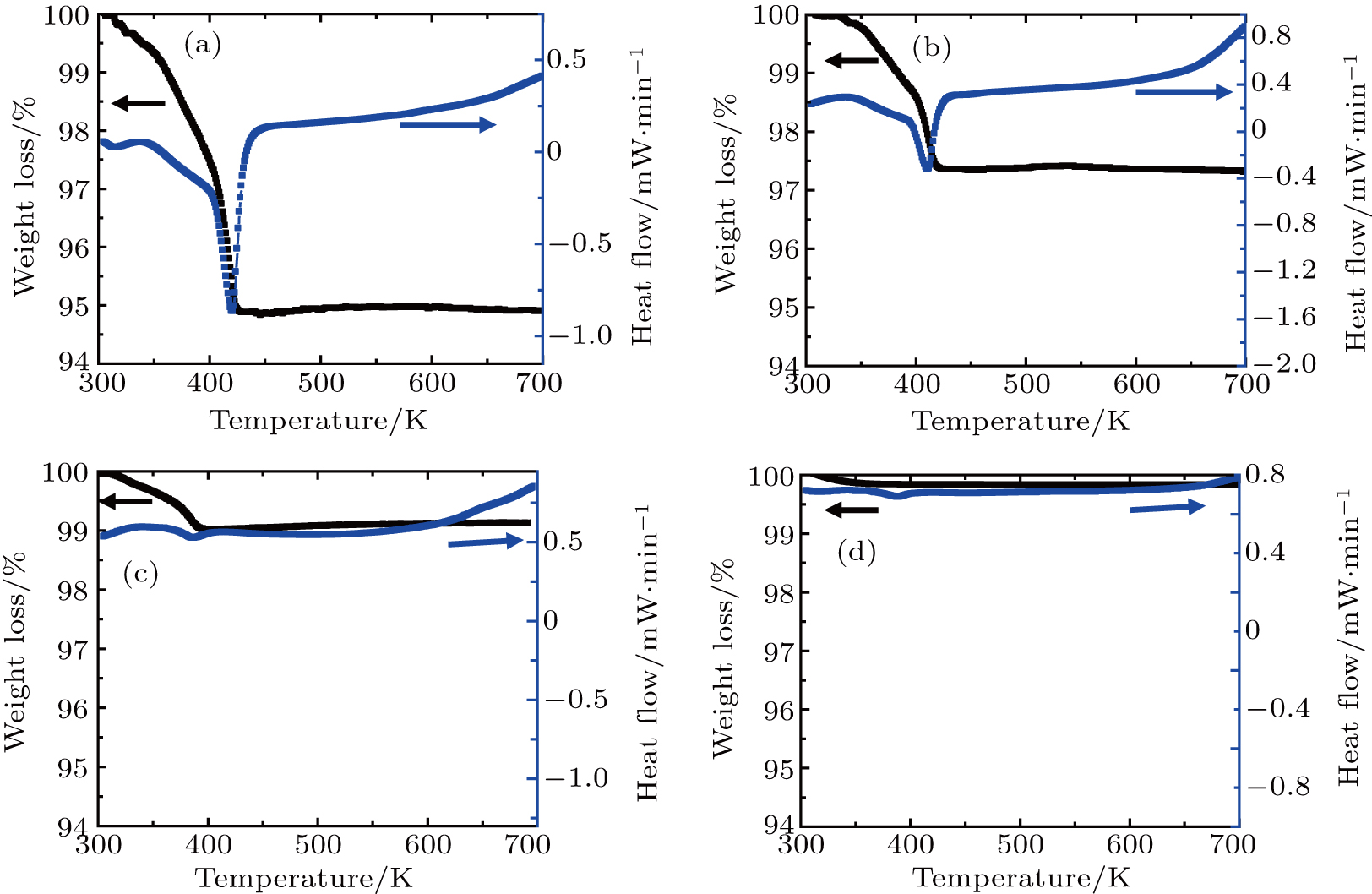
The relative length changes of (LiZn)xMo3O12 with different contents of (LiZn)3+ were measured with increasing temperature (Fig. 5(b)). For x=0.0 (pure Y2Mo3O12), there are two expansion processes and two contraction processes corresponding to the release of adsorbed water and crystal water. Only after the complete release of crystal water, the NET phenomenon is observed. With increasing the content of (LiZn)3+, the thermal expansion and contraction parts corresponding to the release of crystal water become weakened, indicating that the heavy hygroscopicity is reduced remarkably. For the sample of x=0.7, much lower thermal expansion (CTE 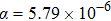K−1, 480–670 K) than that of x=2.0 (CTE 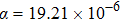K−1, 290–670 K) is obtained besides the reduced hygroscopicity. For the samples of x=1.0 and 1.2, the hygroscopicity is deleted completely and the CTEs ( 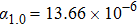K−1, 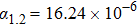K−1, 290–670 K) are reduced obviously comparing with that of .

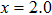Figures 5(a) and 5(b) show that the release process of crystal water is usually accompanied by the relative length change. Therefore, the two expansion processes and two contraction processes of pure Y2Mo3O12 (x=0.0) are drawn together with the release processes of water. Before the release of adsorbed water (blue line part in Fig. 5(c)), the crystal lattice expands with increasing temperature. During the release process of adsorbed water (green line part in Fig. 5(c)), the lattice contracts just like the contraction of seeds by releasing the adsorbed water. For the release process of crystal water (yellow line part in Fig. 5(c)), the lattice presents abrupt expansion and hysteresis. Only after the complete release of crystal water (red line part in Fig. 5(c)), the NET phenomenon is observed. The reduction of hygroscopicity is discussed as follows: the substitutions of Li+ and Zn2+ for Y3+ cause one and two electrons less than the needed three electrons, and then two type ions of (LiY)2− and (ZnY)− form to repel the oxygen in H2O (Fig. 5(d)).

In order to investigate the water change with temperature of Y2−x(LiZn)xMo3O12 with different contents (x=0.1, 0.5, 0.9, 1.0) of (LiZn), TG-DSC curves are presented (Figs. 6(a)–6(d)), where the axis of weight loss is from 100% to 94% for comparison. For x=0.1, the release process of adsorbed water reaches ∼97%, much less than ∼93% of x=0.0 (Fig. 5(c)). The release process of crystal water is from ∼97% to 95%, also less than that from ∼93% to 86% of x=0.0 (Fig. 5(c)). It shows that the adsorbed water and crystal water of the sample with x=0.1 are less than those of the sample with x=0.0. With increasing x from 0.5 to 1.0, the adsorbed water and crystal water reduce remarkably, even close to zero for x=1.0.

Fig. 6. TG-DSC curves of Y2−x(LiZn)xMo3O12 with different contents ((a)–(d) , 0.5, 0.9, 1.0) of (LiZn).
4. Conclusion

The relationships of the laser scattering/transmittance of diverging rays, regular grains, and porosity of Y2−x(LiZn)xMo3O12 with x from 0 to 2.0 are investigated. It is found that the as-prepared ceramic Y2−x(LiZn)xMo3O12 with x= 1.0 and 1.2 present excellent laser scattering/transmittance, regular grains, and less porosity, no hygroscopicity. The result suggests that a certain amount of (LiZn)3+ leads to the reduction of hygroscopicity, the formation of regular grains, less porosity, and then excellent laser scattering/transmittance of diverging rays. The low thermal expansion ceramics of Y2−x(LiZn)xMo3O12 with x= 1.0 and 1.2 could find applications in coating layer with properties of laser scattering and transmittance of diverging rays for reducing harm from strong laser beam.

Reference
[1] Song L Ma H Cheng Y J Zou Y J 2014 Ship. Electron Eng. 34 162 https://doi.org/10.3969/j.issn1672-9730.2014.08.044
[2] Wang X B Ma Z Z 2012 Equip. Environ. Eng. 9 33 https://doi.org/10.3969/j.issn.1672-9242.2012.02.008
[3] Wohlers M R 1972 Appl. Opt. 11 1389 https://doi.org/10.1364/AO.11.001389
[4] Takenaka K Okamoto Y Shinoda T Katayama N Sakai Y 2017 Nat. Commun. 8 14102 https://doi.org/10.1038/ncomms14102
[5] Monroe J A Gehring D Karaman I Arroyave R Brown D W Clausen B 2016 Acta. Mater 102 333 https://doi.org/10.1016/j.actamat.2015.09.012
[6] Ahadi A Matsushita Y Sawaguchi T Sun Q P Tsuchiya K 2017 Acta. Mater 124 79 https://doi.org/10.1016/j.actamat.2016.10.054
[7] Chen J Wang F F Huang Q Z Hu L Song X P Deng J X Yu R B Xing X R 2013 Sci. Rep. 3 2458 https://doi.org/10.1038/srep02458
[8] Yan J Sun Y Wang C Chu L H Shi Z X Deng S H Shi K W Lu H Q 2014 Scr. Mater. 84-85 19 https://doi.org/10.1016/j.scriptamat.2014.04.010
[9] Hu L Chen J Fan L L Ren Y Rong Y C Pan Z Deng J X Yu R B Xing X R 2014 J. Am. Chem. Soc. 136 13566 https://doi.org/10.1021/ja5077487
[10] Chen J Gao Q L Sanson A Jiang X X Huang Q Z Carnera A Rodriguez C G Olivi L Wang L Hu L Lin K Ren Y Lin Z S Wang C Gu L Deng J X Attfield J P Xing X R 2017 Nat. Commun. 8 14441 https://doi.org/10.1038/ncomms14441
[11] Lama P Das R K Smith V J Barbour L J 2014 Chem. Commun. 50 6464 https://doi.org/10.1039/C4CC02634A
[12] Bridges F Keiber T Juhas P Billinge S J L Sutton L Wilde J Kowach G R 2014 Phys. Rev. Lett. 112 045505 https://doi.org/10.1103/PhysRevLett.112.045505
[13] Pryde A K A Hammonds K D Dove M T Heine V Gale J D Warren M C 1996 J. Phys. Condens. Matter 8 10973 https://doi.org/10.1088/0953-8984/8/50/023
[14] Zhang M D Mao Y C Guo J Zhou W J Chao M J Zhang N Yang M J Kong X H Kong X S Liang E J 2017 RSC Adv. 7 3934 https://doi.org/10.1039/C6RA26923K
[15] Wang L Wang F Yuan P F Sun Q Liang E J Jia Y Guo Z X 2013 Mater. Res. Bull. 48 2724 https://doi.org/10.1016/j.materresbull.2013.04.001
[16] Goodwin A L Calleja M Conterio M J Dove M T Evans J S O Keen D A Peters L Tucker M G 2008 Science 319 794 https://doi.org/10.1126/science.1151442
[17] Long Y W Hayashi N Saito T Azuma M Muranaka S Shimakawa Y 2009 Nature 458 60 https://doi.org/10.1038/nature07816
[18] Azuma M Chen W T Seki H Czapski M Olga S Oka K Mizumaki M Watanuki T Ishimatsu N Kawamura N Ishiwata S Tucker M G Shimakawa Y Attfield J P 2011 Nat. Commun. 2 347 https://doi.org/10.1038/ncomms1361
[19] Liang E J Huo H L Wang J P Chao M J 2008 J. Phys. Chem. C 112 6577 https://doi.org/10.1021/jp8013332
[20] Li Q J Yuan B H Song W B Liang E J 2012 Chin. Phys. B 21 046501 https://doi.org/10.1088/1674-1056/21/4/046501
[21] Li Z Y Song W B Liang E J 2011 J. Phys. Chem. C 115 17806 https://doi.org/10.1021/jp201962b
[22] Wu M M Hu Z B Liu Y T Chen D F 2009 Mater Res. Bull. 44 1943 https://doi.org/10.1016/j.materresbull.2009.06.016
[23] Liu H F Wang X C Zhang Z P Chen X B 2012 Ceram. Int. L38 6349 https://dx.doi.org/10.1016/j.ceramint.2012.05.006
[24] Liu X S Cheng Y G Liang E J Chao M J 2014 Phys. Chem. Chem. Phys. 16 12848 https://doi.org/10.1039/c4cp00144c
[25] Liu X S Ge X H Liang E J Zhang W F 2017 Chin. Phys. B 26 108101 https://doi.org/10.1088/1674-1056/26/10/108101
[26] Liu X S Yuan B H Cheng Y G Ge X H Liang E J Zhang W F 2017 Phys. Chem. Chem. Phys. 19 13443 https://doi.org/10.1039/C7CP02262J
[27] Yang G Sun X W Liang E J Zhang W F 2018 Ceram. Int. 44 22032 https://doi.org/10.1016/j.ceramint.2018.08.274
[28] Liu X S Cheng Y G Yuan B H Liang E J Zhang W F 2019 J. Alloys Compd. 776 236 https://doi.org/10.1016/j.jallcom.2018.10.315
[29] Gates S D Lind C 2007 J. Solid State Chem. 180 3510 https://doi.org/10.1016/j.jssc.2007.10.011
[30] Trifonov V A Pavlyuk A A Gorbachenya K N Yasyukevich A S Kuleshov N V 2013 Inorg. Mater 49 517 https://doi.org/10.1134/S0020168513050178
[31] Cheng Y G Liu X S Song W B Yuan B H Wang X L Chao M J Liang E J 2015 Mater. Res. Bull. 65 273 https://doi.org/10.1016/j.materresbull.2015.02.013
[32] Xue L P Wang Y J Lv P W Chen D G Lin Z Liang J K Huang F Xie Z 2009 Cryst. Growth 9 914 https://doi.org/10.1021/cg800700h
[33] Yang X L Zheng Y Liu Z L Dong Z W 2016 Electron. Compo. Mater. 35 6 https://doi.org/10.14106(j.cnki.1001-2028.2016.11.002
[34] He G S Qin H Y Zheng Q 2009 J. Appl. Phys. 105 023110 https://doi.org/10.1063/1.3068473
[35] Prochazka S Scanlan R M 1975 J. Am. Ceram. Soc. 58 72 https://doi.org/10.1111/j.1151-2916.1975.tb18990.x