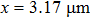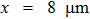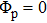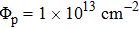† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant Nos. 11775167, 61574171, 11575138, and 11835006).
This paper presents an investigation into the impact of proton-induced alteration of carrier lifetime on the single-event transient (SET) caused by heavy ions in silicon–germanium heterojunction bipolar transistor (SiGe HBT). The ion-induced current transients and integrated charge collections under different proton fluences are obtained based on technology computer-aided design (TCAD) simulation. The results indicate that the impact of carrier lifetime alteration is determined by the dominating charge collection mechanism at the ion incident position and only the long-time diffusion process is affected. With a proton fluence of 5×1013 cm−2, almost no change is found in the transient feature, and the charge collection of events happened in the region enclosed by deep trench isolation (DTI), where prompt funneling collection is the dominating mechanism. Meanwhile, for the events happening outside DTI where diffusion dominates the collection process, the peak value and the duration of the ion-induced current transient both decrease with increasing proton fluence, leading to a great decrease in charge collection.
The electronics in spacecrafts that are routinely exposed to both extreme fluctuations in temperature and energetic particles in space may employ silicon–germanium heterojunction bipolar transistors (SiGe HBT) because of their superior low-temperature performance and built-in multi-Mrad (SiO2) total ionizing dose (TID) tolerance without intentional hardening design.[1–6] However, bulk SiGe HBTs are susceptible to single-event effects (SEEs), which has been proved to be their only obvious weakness for space applications, due to the existence of the large-area collector–substrate (C–S) junction.[7,8] Moreover, existing publications indicate that the sensitive area of SiGe HBTs to SEEs is not just confined in the active region (emitter/base/collector stack). The charges generated in the events many micrometers away from the active region can also be collected through a diffusion process, making the development of the model for on-orbit event rate calculation more complicated.[9,10]
In the space radiation environment, energetic particles can cause several radiation effects in semiconductor devices, including SEEs, TID, and displacement effects, at the same time. The interaction of these effects may lead to unexpected radiation responses of the devices.[11–14] For SiGe HBTs, displacement defects caused by protons in the Van Allen belt and solar galactic cosmic rays can act as effective trapping and recombination centers that can reduce the minority carrier lifetime so that less minority carriers injected from the emitter can cross the base region and reach the collector junction, leading to the degradation of the transistor current gain.[15] However, it is also worth noting that the displacement defects induced by space radiation sources usually distribute uniformly in the whole device. The minority carrier lifetime is also altered in other parts of the device, such as the lightly doped substrate, which is confirmed to be a crucial feature dominating the single-event charge collection of bulk SiGe HBTs. Therefore, the transport of the charges generated in a single event may also be impacted. This may cause changes in the total charge collection, which is the main metric related to single-event upsets (SEU) in SiGe circuits. It has been confirmed that a low-temperature, grown GaAs buffer layer in GaAs HIGFET, which provides a region of high recombination and shortens the minority carrier lifetime, can significantly reduce the transient charge collection caused by the α particle.[16] However, no related publication about SiGe HBT is currently available.
In this work, the impact of proton-induced alteration of minority carrier lifetime on heavy ion-induced current transients and charge collection in SiGe HBT is investigated using technology computer-aided design (TCAD) tools. The results indicate that the charge collection of events free from deep trench isolation (DTI) is more sensitive to the alteration of minority carrier lifetime than that with DTI, especially in the heavily doped reach-through region used for substrate contact, where a decrease of 94% can be found with a proton fluence of 5×1013 cm−2.
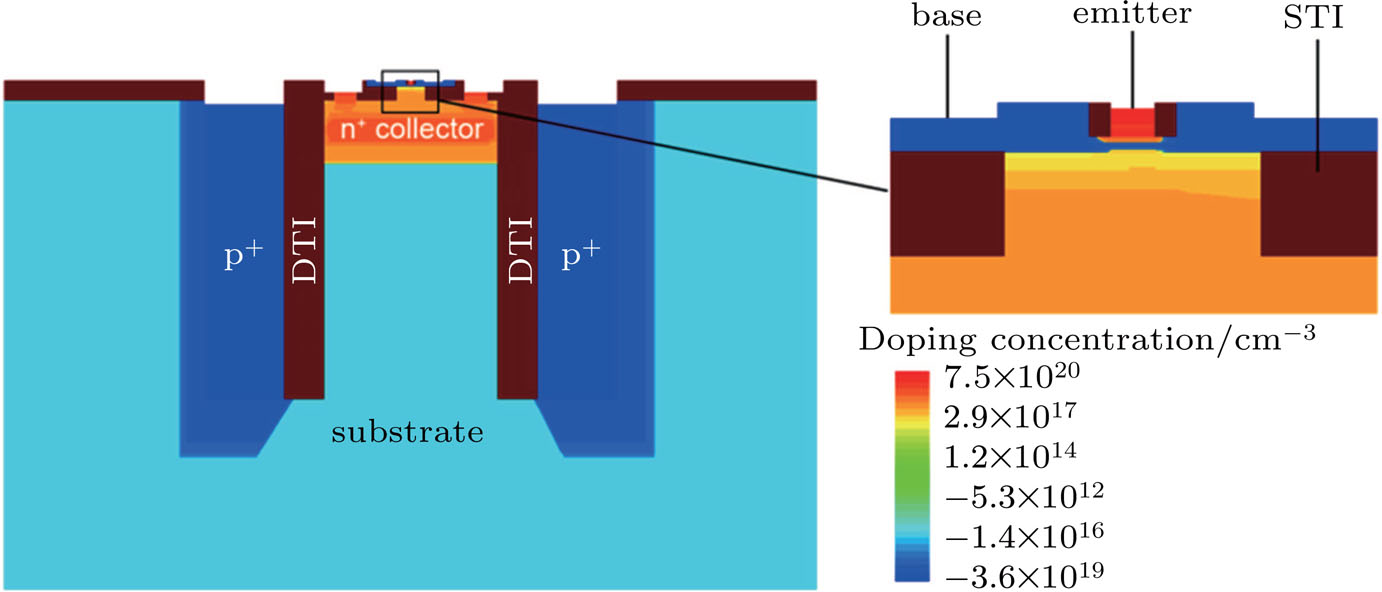
The prototype device used to build the simulation model is the IBM 8HP SiGe HBT. Figure 

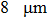

Displacement defects are introduced into the device through collisions of the incident protons with the silicon nucleus and by collisions of the recoil primary silicon atom with near atoms. These defects can act as effective trapping and recombination centers of the carriers. As a result, some basic electric properties of semiconductors, such as the minority carrier lifetime, the majority carrier density, and the carrier mobility, will be altered. The minority carrier lifetime has been proved to be the most sensitive parameter to displacement damage, while the majority carrier density and carrier mobility remain stable with a neutron fluence up to 5×1013 cm−2.[19,20] Therefore, changes in the minority carrier lifetime are usually used to mimic displacement damage in the device. The quantitative relationship between the minority carrier lifetime and displacement damage is usually given involving neutron fluence as follows:



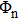




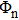

In this work, the 30 MeV proton is selected to generate the lifetime alteration. The NIEL of the 30 MeV proton in silicon calculated using Geant4 is about 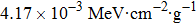

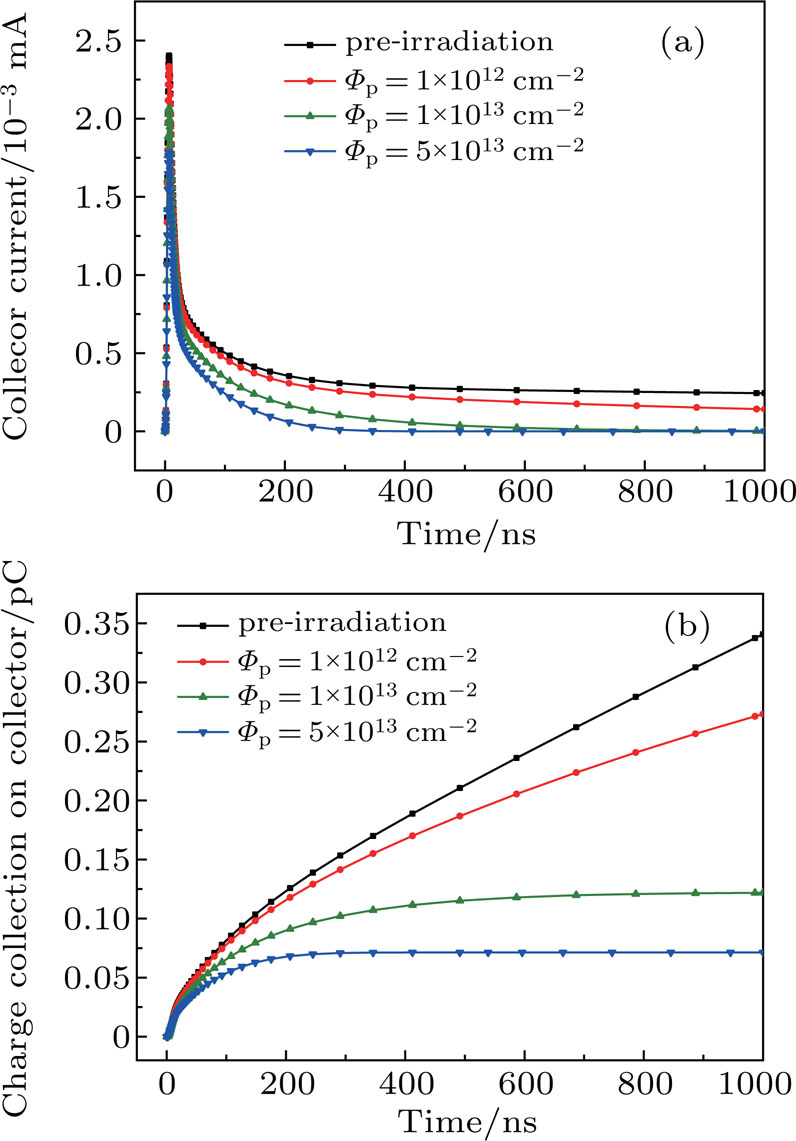
Figure 
This model can also be extrapolated to other SiGe HBT devices. For one thing, the NIEL of middle- and high-energy protons is almost equivalent to that of neutrons.[24] In the real space applications, low-energy protons are easily shielded by the spacecraft walls, and it is hard for the fluence of middle- and high-energy protons to exceed the order of 5×1013 cm−2. Furthermore, the relationship between the minority carrier lifetime and neutron or proton fluence does not involve the geometry of the target material. However, the impact of the alteration of the minority carrier lifetime on the ion-induced single-event transient (SET) may be different from device to device due to the devices’ structures, as will be shown later.
During simulation, the emitter, base, and collector are biased at 0 V, while the substrate is biased at −3 V. Under this condition, the C–S junction is reverse biased. When a heavy ion passes through the junction, the excess carriers deposited can be rapidly collected, leading to a current transient at the collector. Since the collector is usually the output terminal of SiGe HBT in ICs, the ion-induced current transient may cause disturbances in the following components. Therefore, these bias conditions replicate the most sensitive state to SEEs.[25–27] Concretely, the initial voltage boundary conditions of all terminals of the SiGe HBT are set to 0 V in the electrode section of Sentaurus Device, and then these boundary conditions are ramped to the worst biasing conditions in the Solve section of the command file using the quasistationary command. Ohmic contacts are implemented through the Dirichlet boundary condition, in which the quasi Fermi potentials of majority and minority carriers are equal to the applied voltage on the electrode.[28] The outer boundaries of the device that are not contacts are treated with the ideal Neumann boundary condition and the current in the device can only flow through the contacting node. Similarly, the Neumann boundary condition is also applied to the semiconductor/insulator interfaces to avoid the current in the semiconductor from flowing into the insulator. The simulated ion strike is 209Bi with an LET of 99.8 MeV 









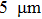



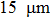
Figure
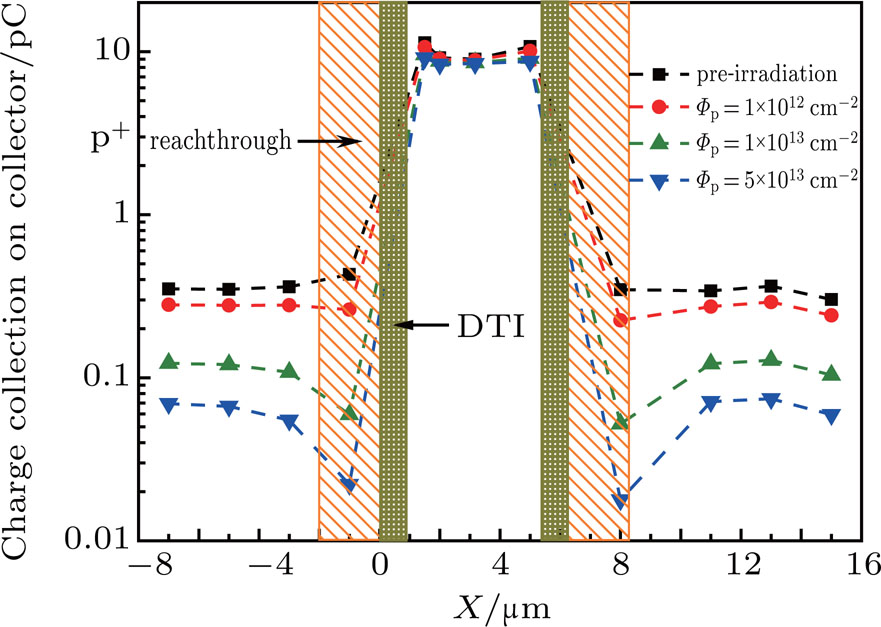
The impact of proton-induced carrier lifetime alteration on the charge collection inside and outside DTI also differs a lot. The lifetime alteration has almost no impact on the charge collection of events happening inside the deep trench, but it does reduce the charge collection of events happening outside the trench by a large extent. With increasing 


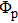
Figure 
Figure 


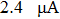

As depicted above, the proton-induced decrease in minority carrier lifetime only reduces the charge collection that is due to the long-time diffusion, and has no impact on the charge collection that is due to funneling. This indicates that the impact of the minority carrier lifetime may be related to the timescale of the collection mechanism. Figure 


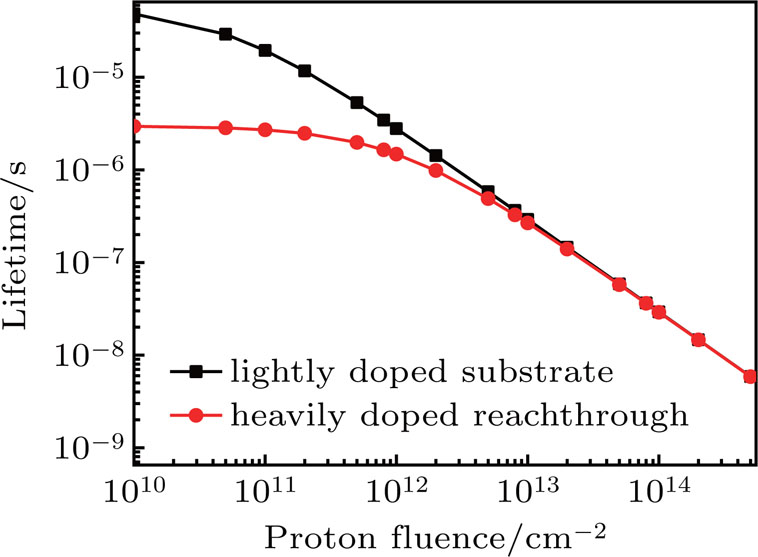
For the events happening in the p+ reach-through, the mechanism is more complicated. Since the doping concentration in the p+ reach-through is several orders of magnitude higher than that in the substrate, the ion-induced electrons and holes have to undergo a stronger initial recombination there. Only the electrons that escape from this recombination and reach the lightly doped substrate through radial diffusion can contribute to the charge collection on the collector terminal. With the increase in proton fluence, more recombination centers are generated in the p+ region, which in turn promotes the initial recombination. As a result, the charge collection of events happening in the p+ reach-through has a more significant decrease with increasing proton fluence. In addition, the pre-irradiation minority carrier lifetime in the p+ reach-through is relatively short, and thus a significant amount of displacement damage is needed to affect it.[20] As shown in Fig. 



In this work, the impact of proton-induced alteration of the minority carrier lifetime on the ion-induced current transient and charge collection in the SiGe HBT with DTI is investigated using TCAD tools. The widely used equation to determine the neutron-induced alteration of the minority carrier lifetime in silicon is extended for use with the to proton by normalizing to the energy going into the atomic process. Simulation results show that the impact of proton-induced alteration of carrier lifetime on the current transient and the integrated charge collection is position-dependent and is closely related to the timescale of the dominating charge collection mechanism. Only the long-time collection process is significantly affected. For the events inside the deep trench, the charge collection is dominated by prompt funneling and is little affected. Meanwhile, for the events outside the deep trench, the charge is collected only by diffusion, and thus a large amount of charges recombine during transport, leading to a great decrease in the total charge collection. Particularly, the decrease is more remarkable in the p+ reach-through due to the enhanced initial recombination of ion-induced charges before they diffuse into the lightly doped substrate.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] |