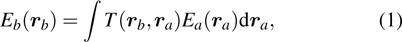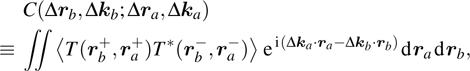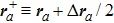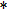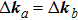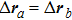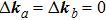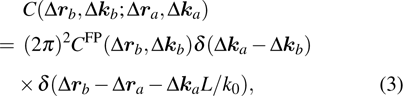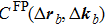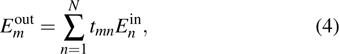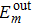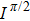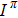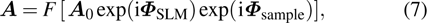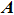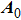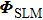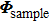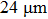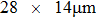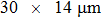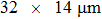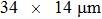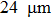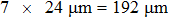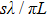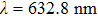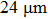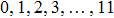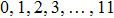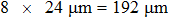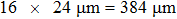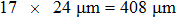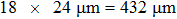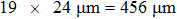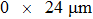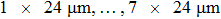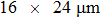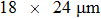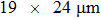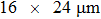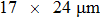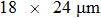College of Physics, Sichuan University, Chengdu 610065, China
† Corresponding author. E-mail:
panglin_p@yahoo.com
Project supported by the National Natural Science Foundation of China (Grant Nos. 61675140 and 61377054) and Graduate Studentʼs Research and Innovation Fund of Sichuan University, China (Grant No. 2018YJSY005).
1. IntroductionTurbid media, such as wood, disordered metamaterials, and living tissues, are opaque because of the strong scattering of light.[1–3] For a long time, it is believed that light scattering is the fundamental limitation for light to propagate through turbid media.[4] As an optical field passes through a medium, its spatial profile becomes randomly perturbed.[5] Luckily, even strongly scattered optical fields still maintain a certain degree of correlation, which can be used to reconstruct clear images from behind scattering media.[4] One of the most widely known correlations is the so-called memory effect, which is firstly proposed by Isaac Freund and coworkers.[6,7] The traditional memory effect describes the following phenomenon: when an input wavefront reaching a diffusing sample is tilted within a certain angular range, the output wavefront is equally tilted. This effect is widely used in imaging through scattering media by point scanning.[8] When the input wavefront is shaped to converge at a spot on the screen, tilting the input wavefront scans the spot on the screen laterally. The memory effect also can be applied to correlation with a known object[9] and off-line reconstruction.[10]
Evaluating the region of the memory effect would be directly measuring the physical shift of the imaged spot[8] or tilting the incident light.[10] In this paper, we proposed to acquire the region of the memory effect by evaluating the transmission matrix of the scattering system. In theory, there is a linear relationship between the incident and transmitted light fields, which is referred by a transmission matrix (TM).[11,12] Measuring TM of a scattering medium is an approach to focus coherent light through scattering media. The optical system of light scattering is a linear system. Under this assumption, a scattering medium could be completely described by TM. Therefore, this approach can work for different targeted patterns at a time, as long as the TM is measured. TM is usually acquired by monitoring the intensity distribution of the transmitted light field when the incident light is modulated by a set of given input patterns, such as Hadamard phase patterns.[11,12] Due to the orthogonality of the Hadamard phase patterns and the flexibility of coherent control of the scattered light, TM approach can be applied to various research fields, such as sub-wavelength imaging[13] and multispectral control.[14] One application of TM evaluation is to achieve the scanning of the focal points, the positions of which can be arranged in the imaging plane regarding to the corresponding TM calculations.[15] The relationship of the focal points reveals the natural properties of the scattering processing.[16]
The knowledge of optical memory effect and the TM approach to focusing light through turbid media have been widely studied and can be applied to many research fields.[9,17–20] However, little work has studied on the relationship between the optimal phase masks of two adjacent focal points. In this paper, we predict that there exists a strong correlation among the optimized phase distributions of adjacent focal points in focusing through scattering media. The finding is verified by both numeric simulation and experiment, which indicate that in the range of the memory effect, the phase difference between the two adjacent focal points shows a linear relationship, or the tilting of the optical phase relation. This effect can be utilized for achieving optimal phase distributions of focal points based on one adjacent focal point in focusing light through scattering media, as well as the quick imaging configuration through the scattering medium.
2. Theory study2.1. Generalized optical memory effectIn many applications including imaging through a thin turbid layer, it is a basic objective to scan a focus in a two-dimensional (2D) or three-dimensional (3D) outgoing plane. However, generating multiple foci at different positions and scanning these reconstructed foci are time consuming and technically challenging. The optical memory effect enables the scanning of a reconstructed optical focus through a scattering layer.
Consider the propagation of monochromatic and coherent light from an input plane a to an output plane b. The input field Ea and the output field Eb are related by[19]
where
is the sampleʼs TM, and
and
are the position vectors in the input plane and output plane, respectively. The translation distance within which the optical memory effect holds (that is, the field of view (FOV)) is inversely proportional to sample thickness
L and directly proportional to the distance
s of the sample from the screen. It can be approximated by the equation
[18]where (
λ is the wavelength of light. Within this range, when the incident wave is shifted by
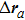
and tilted by
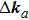
, the output wave is shifted by
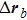
and tilted by
. One important branch of the theoretical studies is the random matrix theory (RMT), in which the correlations between the propagating modes inside the scattering media are examined based on the scattering matrix. Here, we list a generalized tilt/shift correlation function, which is defined as
[18]where
,
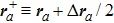
(the same for
, and
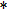
stands for the conjugate transpose. In the special case that
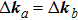
and
, equation (
3) reduces to the optical tilt memory effect, whereas for
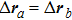
and
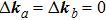
, the correlation function corresponds to the shift memory effect. The approximate solution of the correlation function for forward scattering is given by
[19]where
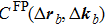
is a 2D Fokker–Planck correlation function,
[19] and
k0 is the wave number. As is clear from Eq. (
3), the shift and tilt correlations along the output plane are not independent, but show a combined effect. The two
δ functions are a direct result of the shift and tilt invariance of the Fokker–Planck model.
[21–23]The schematic of our work is shown in Fig. 1. When the input wavefront is shaped by a spatial light modulator (SLM) to converge at a spot on the screen. When a coherent wave propagates through disordered media, the addition of a small phase gradient to the incident field (i.e., tilting of the incident field) results in the addition of the same phase gradient to the corresponding transmitted field. Therefore, once an incident wavefront is optimized such that the optical focus is generated at a target position behind a scattering layer, the generated focus can be translated by adding a small phase gradient to the optimized wavefront or tilting the incident wavefront using a mirror or an SLM.
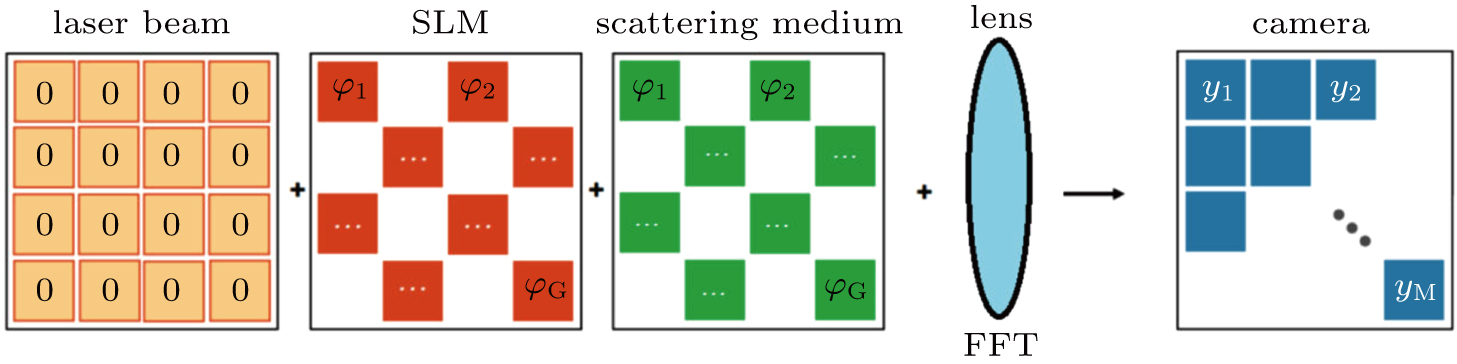
2.2. Transmission matrix approachIn the scattering processing, the input field and output field can be described as the input channels and output channels. The light channels are the amplitude or phase modes of light fields. Therefore, equation (1) can be rewritten as[1]
where
(
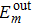
) is the electric field at the
output channel,
(
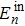
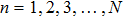
) is the electric field at the
nth input channel, and
tmn are the elements of the TM.
The TM approach exploits a set of predefined phase distributions and requires four measurements for each input mode. The observed TM is obtained by calculating the complex light field corresponding to a set of given input modes. The Hadamard basis set is selected, because it can be represented as a phase basis with uniform amplitude. The complex electric field response is measured by interference between the Hadamard basis elements and known phase reference beams, where we use a four-phase approach to reconstruct the complex light field. Each Hadamard basis element interferes with phase references of 0, (π/2, (π, and 3(π/2 and is detected after propagation through the random scattering layers. The observed TM response for Hadamard basis element n is calculated with the intensity measurements at the output mode from all four phase references (I0,
,
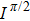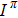, and
) according to[11]
where
(
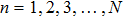
) is the
nth element of the observed TM
Kobs. The optimized phase distribution for creating a focus at the single output mode is calculated as
[11]where H represents the conjugate transpose. The procedure described above is the approach to measure the TM for a single output mode. We have measured the transmission matrices of the focal points. It is impossible to measure the whole TM of the scattering media. We only concern about the phase distributions of focal points. By using the measured transmission matrices, the focal points can be attained by conjugating the phases of the transmission matrices. As mentioned above, the TM approach can work for different target patterns at a time, as long as the TM is measured.
Both tilting the incident light into the scattering medium and TM evaluating could shift the output mode (focal points) through the scattering medium, which indicates the essential correlation between these two factors. This also reveals that we could evaluate the region of the memory effect by comparing the optical phases of the adjacent output modes, or focal points, through calculating the transmission matrix of the scattering system. In the following sections, we study the correlation of the optimal phase distributions of adjacent focal points in the range of the memory effect through the TM evaluation approach by both numeric simulation and experiment.
3. Numeric simulationThe TM simulation model is shown in Fig. 2. The incident plane wave is represented by a matrix consisted of N elements with phase 0, and the magnitudes of all the elements are set to 1. The plane wave is incident on a spatial light modulator. The phase-only modulator can be seen as a matrix with complex numbers N in which their moduli are ones and phases can be changed. The spatially phase shaped wave is incident on a strongly scattering sample, which is represented by a random matrix with circular Gaussian distribution. After propagating through the turbid medium, the scattered light is collected by a CCD, which could be represented by an operation of Fourier transform (FT). The whole procedure can be expressed as[17]
where
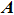
is the complex amplitude distribution in the output plane,
F represents the Fourier transform,
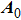
represents the complex amplitude in the incident plane wave,
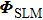
is the phase-only modulation on SLM, and
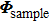
is the phase modulation of the sample. The intensity distribution in the output plane is given by
.
[2] In order to emulate the experimental noises in actual measurements, we add 1% of the average speckle intensity to simulate the noise.
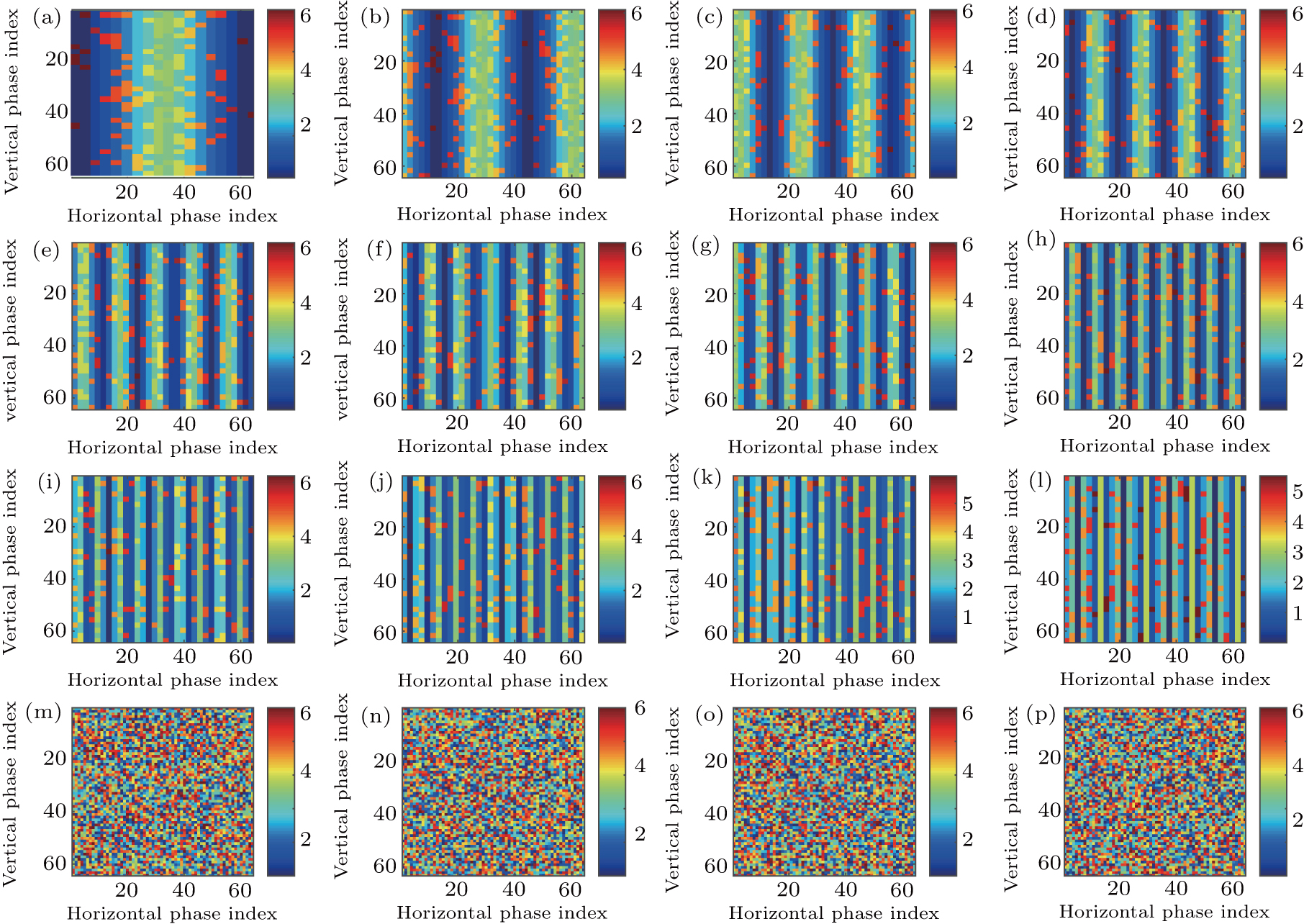
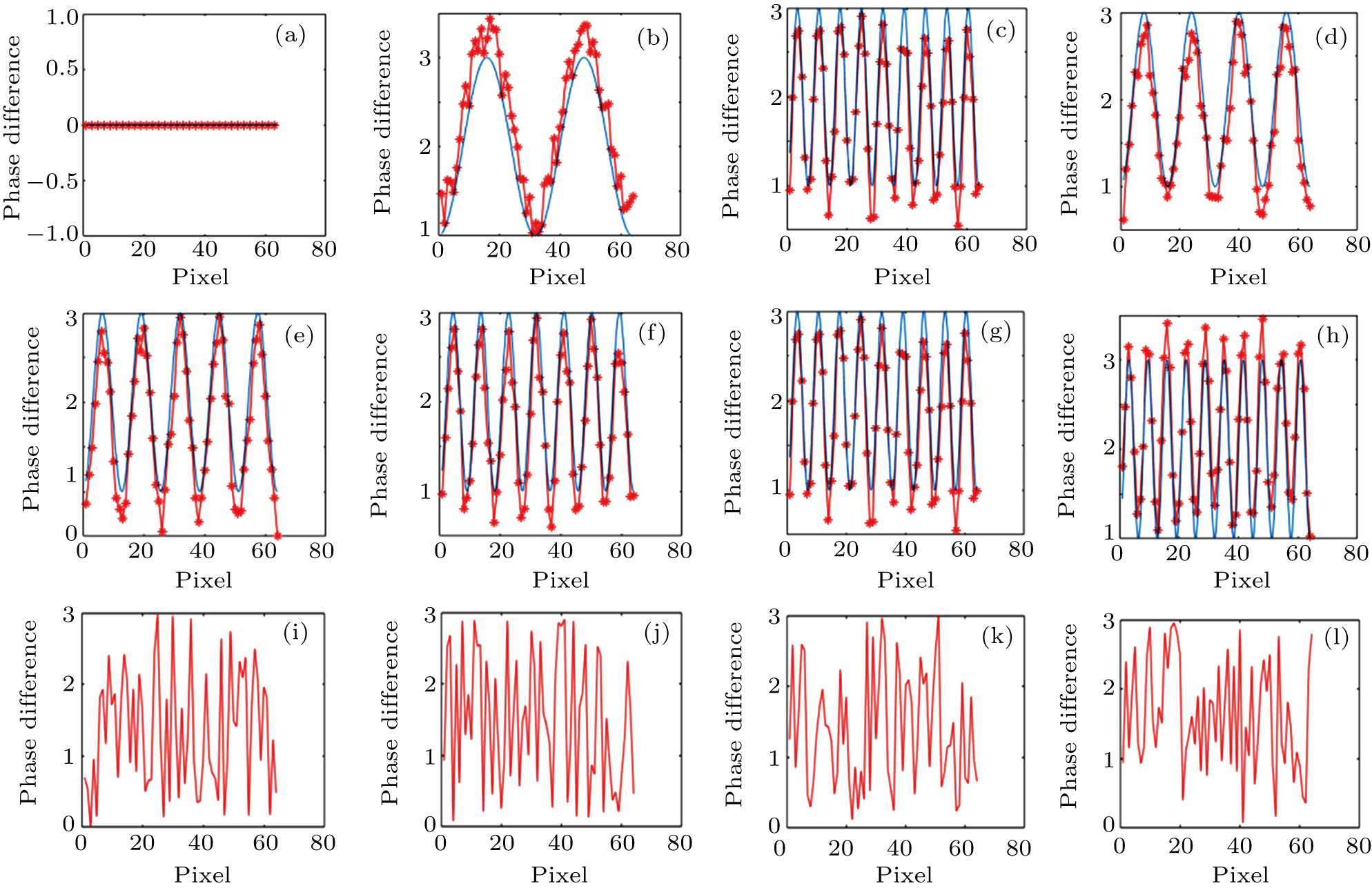
Figure 3 shows the positions of the focal points on the CCD screen by employing the evaluated optical phases via the transmission matrix of the scattering system on the SLM. The distances between the focal point of Fig. 3(a) and that of Figs. 3(b)–3(l) are in the the range of memory effect, while the distances between the focal point of Fig. 3(a) and that of Figs. 3(m)–3(p) are outside the range of memory effect. The focal points are listed from left to right and the intensity of the focal point is normalized to the incident light. The number of pixels on the CCD screen is 64×64=4096. Employing the TM approach mentioned above, 16 optimal phase distributions for the focal points in Fig. 3 can be obtained. From Fig. 3(a) to Fig. 3(l), each picture moves by one pixel on the screen of the CCD. For Fig. 3(l), the focal point totally moves by 12 pixels on the screen. Figure 3(m)–3(p) show the focal points on the CCD screen in which the distances are outside the range of optical memory effect. The focal points with respect to that in Fig. 3(a) move by 16 pixels, 17 pixels, 18 pixels, and 19 pixels, respectively. The normalized intensities of the focal points in Figs. 3(a)–3(p) are listed in Table 1. From Table 1, it can be seen that the intensities have minor differences among the 16 focal points, indicating that there exist noises in the process of focusing. The reason of adding noise in the optimization process of the TM approach will be discussed in detail in Section 5. We calculate the phase differences between the corresponded first focal point in Fig. 3 and the rest focal points, which are shown in Fig. 4. The number of pixels of the SLM is 64×64=4096. From Figs. 4(a)–4(l), it can be seen that, when the distances are in the range of memory effect, the phase differences show optical phase fringe patterns, and the closer the focal points are, the wider the fringe periodicities are. The optical phase gradients and their variations shown in Figs. 4(a)–4(l) reveal that the optical phase differences are linear optical phases, which correspond to plane waves. The periodicity increase of the phase gradient shows the rotation of the plane waves. The phase gradient along the horizontal direction can be expressed as
 | |
where
x is the deviation from the optical axis, and
k is a fitting parameter. In other words, the differences reveal that after acquiring the optimal phase distribution corresponding to a focal point using an iterative approach (for example, the GA), we could obtain the optical phases to form the focal points at any defined positions by directly adding the phase gradient to the optimized optical phase distribution. Of course, the formed focal points should lie in the range of optical memory effect. From Figs.
4(m)–
4(p), it can be seen that, when the distances are outside the range of optical memory effect, the phase differences exhibit random phase patterns, indicating that there exist no correlations under this condition. Note that although the number of segments of the CCD screen is limited, these random phase difference patterns are due to the large distances between the original focal point and the moved focal points, rather than the limited number of pixels of the CCD screen.
Table 1.
Table 1.
 Table 1.
The normalized intensities of focal points in Figs. 3(a)–3(p).
.
| Figure |
3(a) |
3(b) |
3(c) |
3(d) |
3(e) |
3(f) |
| Intensity |
0.8356 |
0.8344 |
1 |
0.8999 |
0.9312 |
0.9007 |
| Figure |
3(g) |
3(h) |
3(i) |
3(j) |
3(k) |
3(l) |
| Intensity |
0.8516 |
0.8936 |
0.8351 |
0.8201 |
0.8107 |
0.9845 |
| Figure |
3(m) |
3(n) |
3(o) |
3(p) |
|
|
| Intensity |
0.9563 |
0.9572 |
0.8746 |
0.8329 |
|
|
| Table 1.
The normalized intensities of focal points in Figs. 3(a)–3(p).
. |
Figure 5 shows the phase difference profiles along one direction shown in Fig. 4, which clearly reflects the inclinations of phase gradients. We decrease the magnitude of noise levels through averaging the vertical phase values of the gradient patterns. The asterisks denote the simulated phase differences, while the blue curves denote the observed fringe patterns. Note that there are many saw-tooth structures in Fig. 5, which correspond to phase inclination and wavefront tilting. From Fig. 5, it can be seen that, when the distance between two focal points increases, the number of peaks in Fig. 5 increases. In Figs. 5(a)–5(l), the number of peaks is
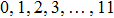, respectively. The inclinations of phase gradients reflect the direction of the wave vector of the output wavefront. Moreover, the peak values of the plots are not definitely the same due to the measurement noises added in the simulation process. From Figs. 5(m)–5(p), it can be seen that, when the distances are outside the range of optical memory effect, the phase differences along the central horizontal direction exhibit random phase profiles, indicating that there exist no correlations under this condition. Therefore, we can conclude from the numeric simulation that, inside the range of optical memory effect, the phase differences between the two adjacent focal points are phase gradients, and the further the adjacent focal points are, the larger the inclination of the output wavefront will be. The essence of the phase gradient is the tilting of a plane wave phase added onto the acquired optical phase distribution at the first focal point. Once an incident wavefront is optimized such that the optical focus is generated at a target position behind a scattering layer, the generated focus can be translated by adding a small phase gradient to the optimized wavefront using a mirror or through tilting the incident wavefront using an SLM.
4. ExperimentThe scattering medium we used in the experiment comprises a layer of
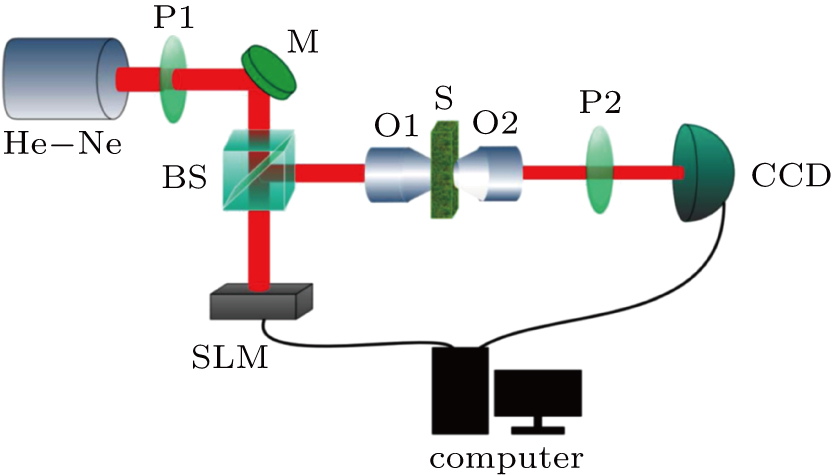
(average diameter) Al2O3 spheres diffused in polydimethylsiloxane (PDMS), which is spray-painted onto a standard glass microscope cover slip. The experimental setup is shown in Fig. 6. A He–Ne laser beam with 632.8 nm wavelength is spatially filtered and collimated to become a plane wave after passing through a microscope objective (not shown in the figure) and a polarizer P1. The polarizer P1 is used to select the polarization state for which the modulator works. The plane wave is incident on a phase-only SLM (Holoeye HEO 1080P). The phase-modulated light is reflected and redirected by a beam splitter BS, focused on the surface of the scattering medium by an objective lens (10 ×, NA = 0.25). A 20×objective lens (NA=0.4) is used to image the scattered light onto a CCD camera (Point Grey Research Grasshopper, pixel number 1920 × 1200). The scattering medium in this experiment is a ground glass, in which depolarization would happen when light propagates through the medium. Therefore, the polarizer P2 is used to filter depolarized photons. The intensity distribution in the output plane is transferred to a computer and the feedback signal is used to control the spatial light modulator.
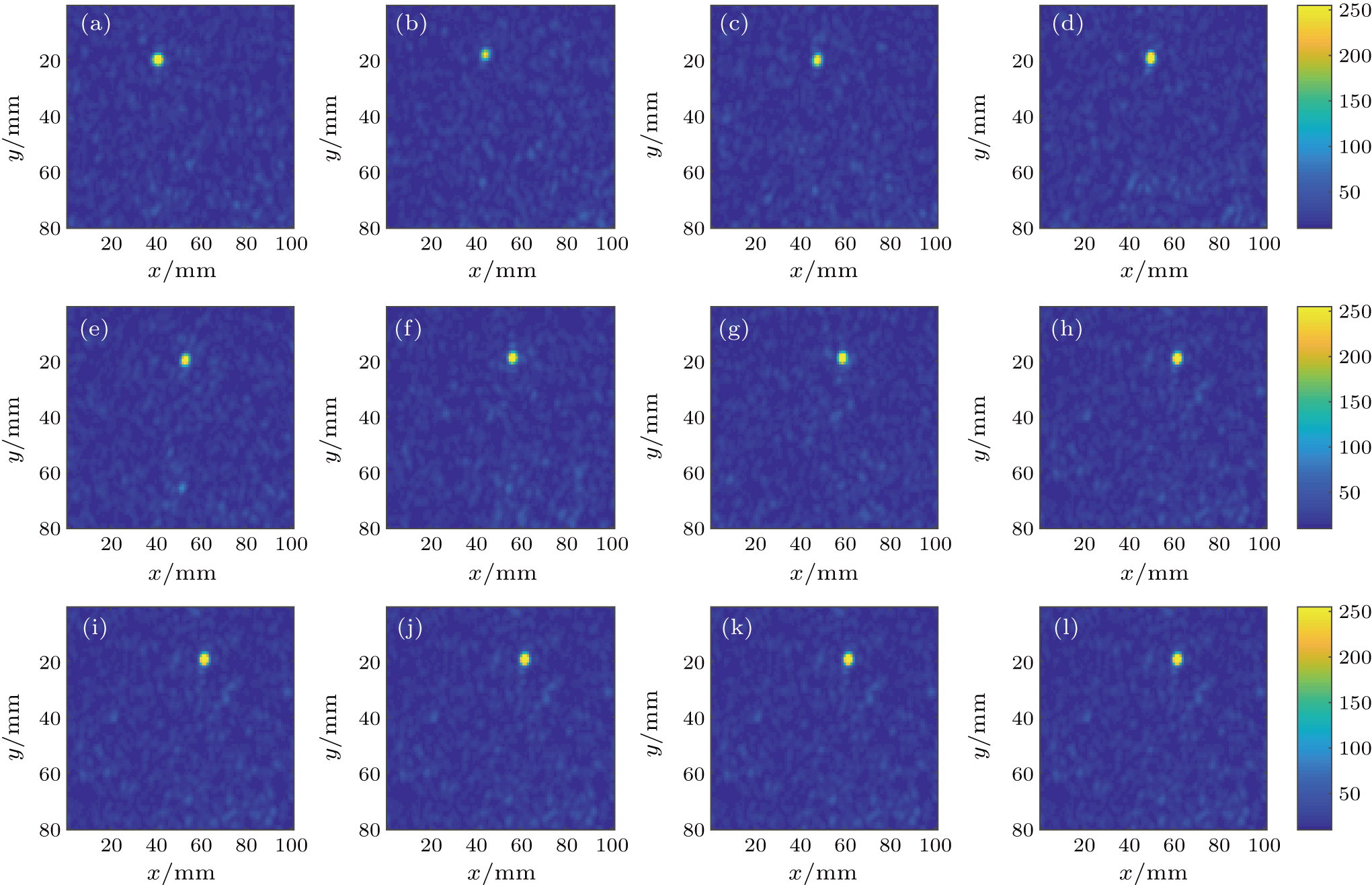
In this work, we use the TM approach (see subSection 2.2) to optimize the phase distribution of the spatial light modulator. We totally perform the experiment for 12 times, and 12 focal points and their corresponding phase masks can be obtained. In the range of memory effect, each time the target point moves by two pixels. Thus, the 8 focal points are adjacent on the CCD screen, where the central coordinates of the focal points are [20, 40], [20, 42], [20, 44], [20, 46], [20, 48], [20, 50], [20, 52], and [20, 54], respectively. We integrate the intensity of 3 × 3 pixels around the central points to save in a computer as the feedback signal to control the spatial light modulator. Figure 7(a)–7(h) show the positions of the focal points shot by the CCD experimentally. Each time the focal point on the screen moves by
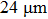. The focal points are listed from left to right, in which the intensity is normalized to the incident light. The number of pixels on the CCD screen is 80 × 100 = 8000. When the distances are outside the range of optical memory effect (see Figs. 7(i)–7(l)), the central coordinates of the focal points are [20, 68], [20, 70], [20, 72], and [20, 74]. We integrate the intensity of 3 × 3 pixels around the central points to save in a computer as the feedback signal to control the spatial light modulator. In Figs. 7(i)–7(l), the focal points move by
,
,
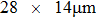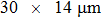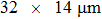, and
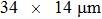, respectively. The normalized intensities of the focal points in Figs. 7(a)–7(l) are listed in Table 2, which reflect the quality of foci. From Table 2, it can be seen that the intensities have minor differences among the 12 focal points, indicating that there exist noises in the process of focusing.
Table 2.
Table 2.
Table 2.
The normalized intensities of focal points in Figs. 7(a)–7(l).
.
| Figure |
7(a) |
7(b) |
7(c) |
7(d) |
| Intensity |
0.9936 |
0.9351 |
1 |
0.9107 |
| Figure |
7(e) |
7(f) |
7(g) |
7(h) |
| Intensity |
0.8699 |
0.8193 |
0.8201 |
0.8791 |
| Figure |
7(i) |
7(j) |
7(k) |
7(l) |
| Intensity |
0.9812 |
0.9156 |
0.8754 |
0.8937 |
| Table 2.
The normalized intensities of focal points in Figs. 7(a)–7(l).
. |
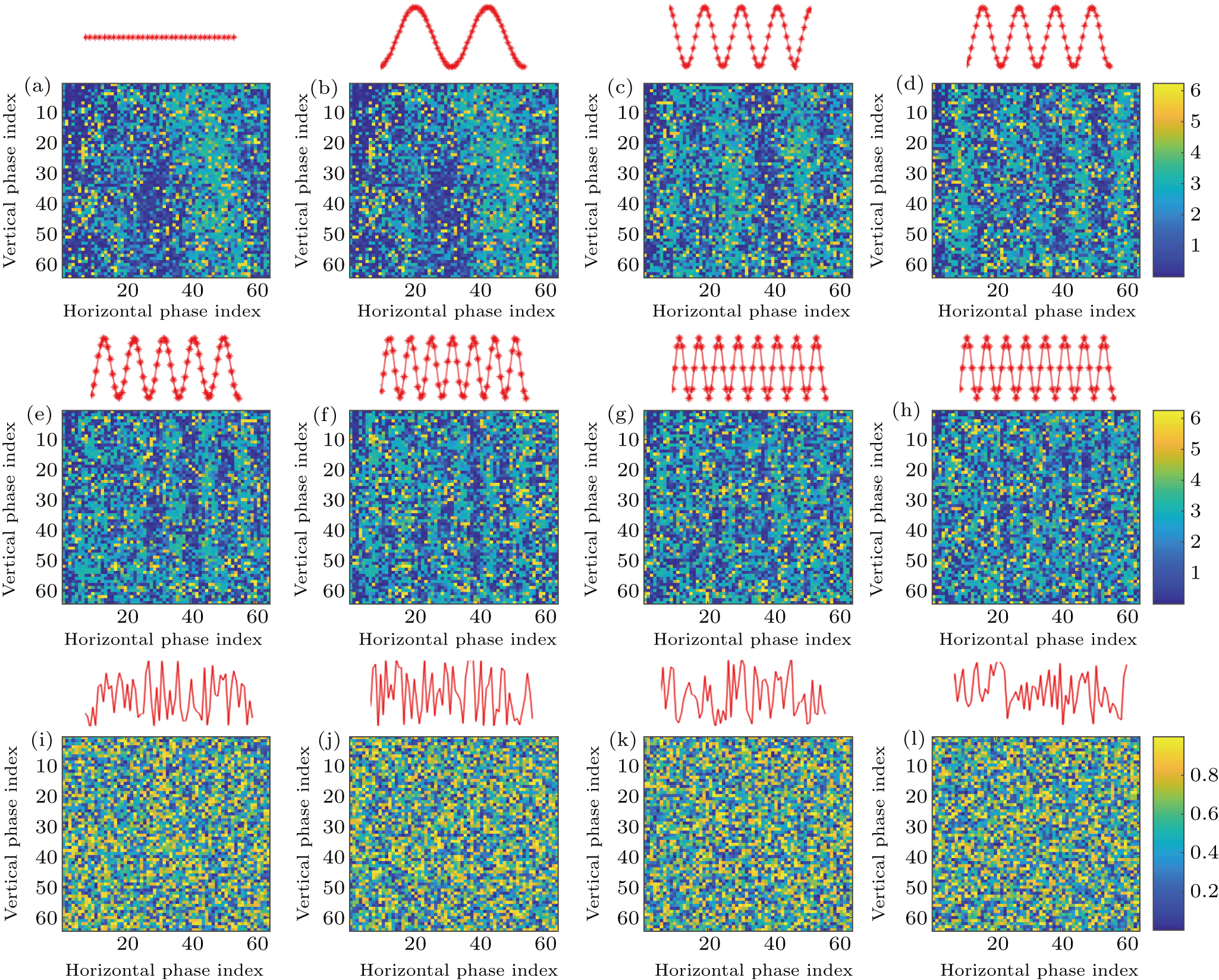
Figure 8 shows the phase differences of focal points measured experimentally. The independently controlled number of segments of the SLM is 64 × 64 = 4096. When the distances are in the range of optical memory effect (see Figs. 8(a)–8(h)), each time the focal point on the screen moves by
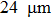, and the distance between the scattering medium and the screen (i.e., the CCD) is 10 cm. Therefore, each time the wavefront rotates 0.72 mrad. Since there exist some measurement noises in the process of focusing, we portray the fringe patterns to guide eyes. The red curves are the portrayed phase masks to guide eyes for observation, while the fuzzy fringe patterns show the experimental values. The number of vertical fringes in Figs. 8(a)–8(h) is 0, 2, 4, 4, 5, 7, 9, and 10, respectively. When the distance of two focal points increases, the magnitude of the phase gradient increases simultaneously, indicating that the tilting angle of the output wavefront increases. When the focal point moves by
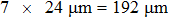, which means the wavefront rotates 7 × 0.72 mrad = 5.04 mrad, the phase gradient pattern gradually disappears. Commercially available CCDs have a maximum full-image frame rate of 41 fps, the possible number of segments available under this condition is limited. For this reason, we combine the 1920 × 1200 array of pixels into 960 × 600 segments. As a result, we are able to take advantage of the high frame rate of CCDs. Thus, the resolution of the phase gradients is limited by the number of pixels, and the range of optical memory effect for this medium is larger than 5.04 mrad. As mentioned above, the theoretical FOV of the system is
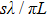. In this experiment, s = 10 cm,
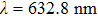, and
. Thus, FOV can be estimated as 8 mrad, which has a magnitude equal to that of the experimental values. When the distances are outside the range of memory effect (see Figs. 8(i)–8(l)), the phase differences exist random phase patterns, indicating that the correlations of the wavefront disappear. Figure 9 shows the phase difference profiles along one direction of Fig. 8 by subtracting the calculated optical phase of the first focal point from the rest, which clearly reflects the magnitude of phase gradient. The asterisks denote the smoothed experimental phase differences, while the blue curves denote the observed phase gradient patterns to guide eyes. Note that there are many saw-tooth structures in Figs. 9(a)–9(h). These saw-tooth structures represent phase gradients and wavefront tilting. For the phase differences in the range of memory effect (see Figs. 9(a)–9(h)), when the distance between two focal points increases, the number of peaks increases. The magnitude of the phase gradient reflects the inclination of the output wavefront. Moreover, the peak values of the figures are different due to the measurement noise in the process of experiment. Therefore, we can conclude from the experiment that, in the range of optical memory effect, the phase difference between the two adjacent focal points shows an optical phase gradient pattern, and the longer the adjacent focal points are, the smaller the magnitude of the phase gradient will be, corresponding to the tilting of a plane wave phase added onto the acquired optical phase distribution at the first focal point. When the focal point on the screen moves by
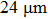, the inclination of the phase gradient is 0.72 mrad. As shown in Fig. 8(h), the total number of peaks is 10. Hence the FOV of this system is estimated to be larger than 5 mrad, due to the limitation of the resolution of the CCD. As mentioned above, the essence of the phase gradient is the tilting of the plane wave phase added onto the acquired optical phase distribution at the first focal point. Once an incident wavefront is optimized such that the optical focus is generated at a target position behind a scattering layer, the generated focus can be translated by adding a small phase gradient to the optimized wavefront using a mirror or through tilting the incident wavefront using an SLM. This conclusion is in accordance with the theoretical result. When the distances of the focal points are outside the range of memory effect (see Figs. 9(i)–9(l)), the phase difference profiles exhibit random phase curves, indicating that there exist no correlations between the original wavefront and translated wavefront.
5. DiscussionIn the simulation part, the phase fringe patterns are ordered, while in the experiment part, the definition and resolution of the fringe patterns decrease due to the fact that there exist measurement noises in the process of optimization. The noise during the optimization process for focusing light through random scattering media includes (i) the shot noise, which is due to the random fluctuation of the photon flux arrived at the CCD, (ii) the quantization noise, which is produced during the conversion of analog signal to digital signal by CCD and computer, (iii) the thermal noise in the environment, and (iv) the random noise due to the fluctuation of the output power of laser. The noise affects the optimized phase distribution, which leads to a reduction of the enhancement. In this part, we emphasize background noise in our laboratory. Although the experiment was carried out in a dark environment, the interference of background light and light source instability could not be completely removed.
Since the recording frequency of CCD in this experiment is 40 Hz, when the number of segments is 64 × 64 = 4096, the focusing procedure would take several minutes to reach the optimization. If the digital micro-mirror device (DMD) is employed as the phase modulator, in which reading frequency could reach up to 20 kHz, the optimized phase distribution can be achieved within a millisecond when the segment number is 64 × 64 = 4096. DMD can be used to generate binary amplitude holography for phase modulation. We generate an amplitude hologram using the Lee method. It means that focusing light through living tissue could be achieved, a door in vivo deep tissue imaging may be opened for broad applications.
6. ConclusionWe have demonstrated that there exists a strong correlation among the optimized phase distributions of adjacent focal points in focusing through scattering media. The numeric simulation and experiment indicate that in the range of memory effect, the phase difference between the two adjacent focal points shows a fringe pattern, and the closer the adjacent focal points are, the wider the fringe pattern will be. This work may provide a precise and nondestructive method for the analysis of a wide variety of turbid media, which has a crucial role in imaging through scattering media, transmission matrix correlation research, and even pharmacy.
