† Corresponding author. E-mail:
Project supported by the National Key R&D Program of China (Grant No. 2017YFB0405703), the Ministry of Science and Technology of China (Grant Nos. 2018YFA03057001 and 2015CB921000), and the National Natural Science Foundation of China through the Research Projects (Grant Nos. 11534016 and 61504166).
Chemical pressure induced by iso-valent doping has been widely employed to tune physical properties of materials. In this work, we report effects of chemical pressure by substitution of Sb or P into As on a recently discovered diluted magnetic semiconductor (Ba,K)(Zn,Mn)2As2, which has the record of reliable Curie temperature of 230 K due to independent charge and spin doping. Sb and P are substituted into As-site to produce negative and positive chemical pressures, respectively. X-ray diffraction results demonstrate the successful chemical solution of dopants. Magnetic properties of both K-under-doped and K-optimal-doped samples are effectively tuned by Sb- and P-doping. The Hall effect measurements do not show decrease in carrier concentrations upon Sb- and P-doping. Impressively, magnetoresistance is significantly improved from 7% to 27% by only 10% P-doping, successfully extending potential application of (Ba,K)(Zn,Mn)2As2.
A dilute magnetic semiconductor (DMS), which has potential to control charge and spin in a single material, is very applicable to spintronic devices.[1–3] Since the discoveries of (Ga,Mn)As and (In,Mn)As, the III–V based DMSs have received much attention as prototypical DMS materials.[4–6] However, in either (Ga,Mn)As or (In,Mn)As, heterovalent (Ga3+, Mn2+) or (In3+, Mn2+) substitution leads to difficulties in individual control of carrier and spin doping and seriously limited chemical solubility. These two obstacles prevent further improving the Curie temperature (TC) of the III–V based DMS.
Recently, a series of new DMS materials with independent doping of carrier and spin have been discovered, such as Li(Zn,Mn)As and (Ba,K)(Zn,Mn)2As2 (BZA).[7,8] Many progresses have been made in these new DMSs on both fundamental studies and potential applications.[9–28] Among the new DMS materials, BZA has a maximum Curie temperature (TC) of 230 K, which is a reliable record of carrier-mediated ferromagnetic DMS.[29] Large single crystals of BZA have been grown.[15] Taking advantage of single crystal-based Andreev reflection junction, the spin polarization rate of 66% is obtained for BZA, which is comparable to prototypical III–V based DMS.[15,30]
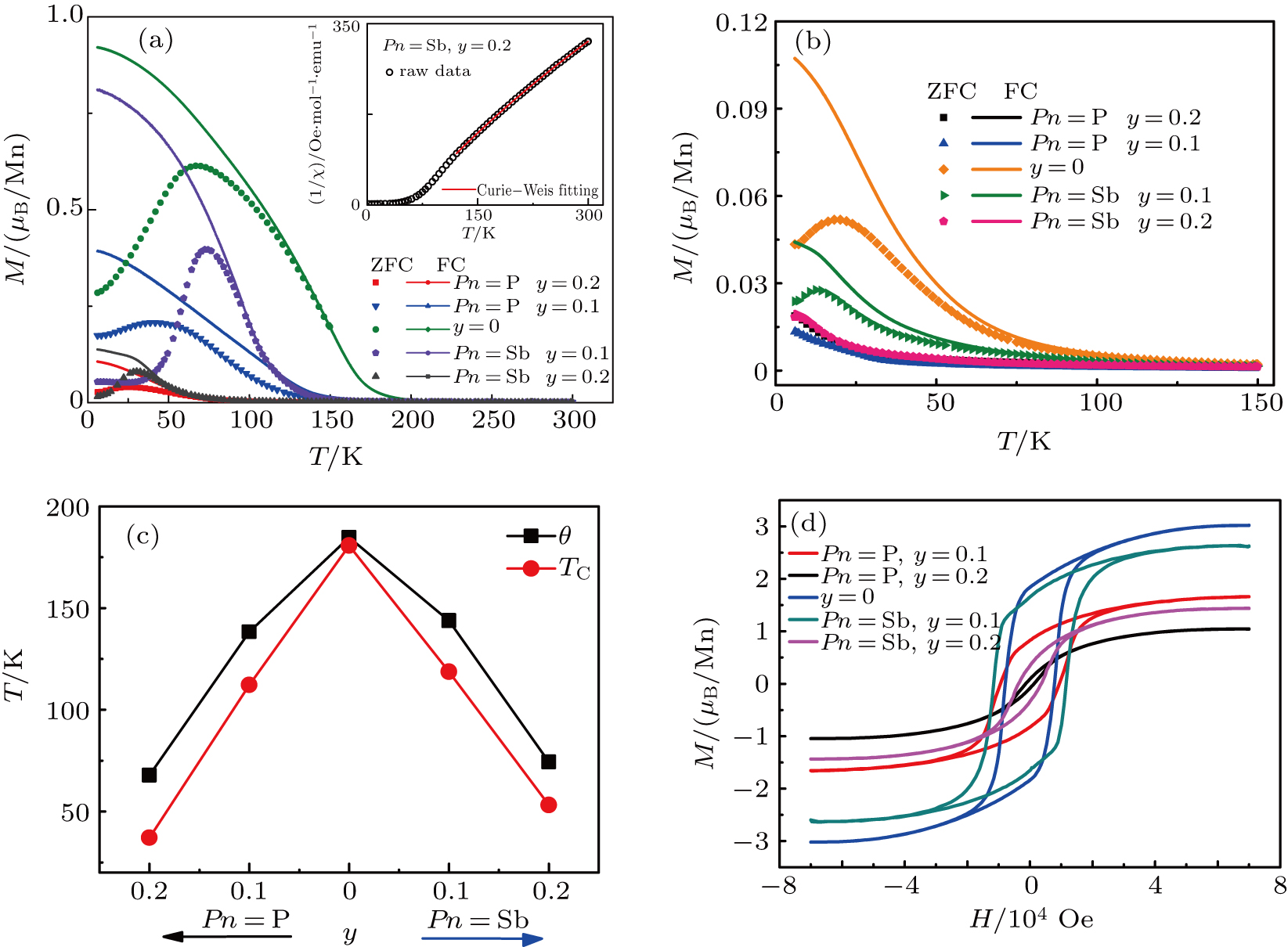
However, the lack of reliable room temperature ferromagnetism is still one of the open questions for all DMS materials. Recently, a series of studies have concentrated on physical pressure-effect on BZA to gain an insight into the mechanism of the ferromagnetism in BZA and in turn to search for a possible way to increase TC. Although these works showed suppression of TC with increasing external pressure, one may wonder how lattice expansion will affect the ferromagnetism in BZA. In this article, we substitute As with Sb and P to study the negative and positive chemical pressure-effect on BZA.
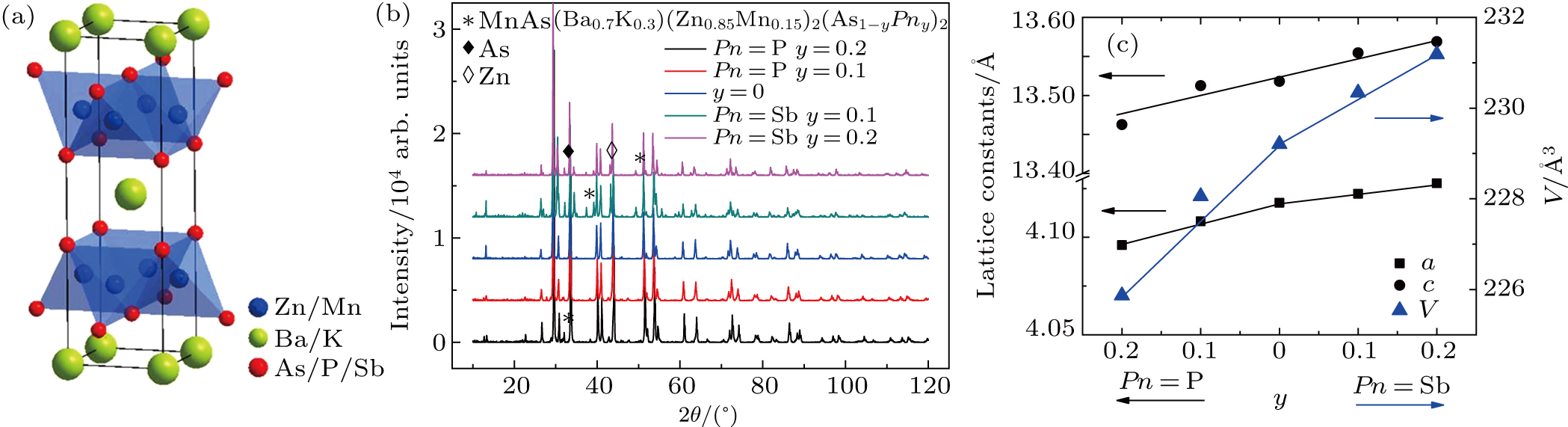
Two teams of samples have been synthesized: the first is based on K-under-doped (Ba0.9K0.1)(Zn0.85Mn0.15)2(As1−yPny)2 (Pn = Sb and P; y = 0.1 and 0.2), the second is based on K-optimal-doped (Ba0.7K0.3)(Zn0.85Mn0.15)2(As1−yPny)2 (Pn = Sb and P; y = 0.1 and 0.2). The polycrystallines of all the samples were synthesized with conventional solid reaction under the protection of high-purity argon as described in Ref. [8]. Powder x-ray diffraction (PXRD) was performed using Cu 
All the samples crystalize into tetrahedral BaZn2As2 phase (β-phase, space group 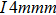
Figures 

Figure
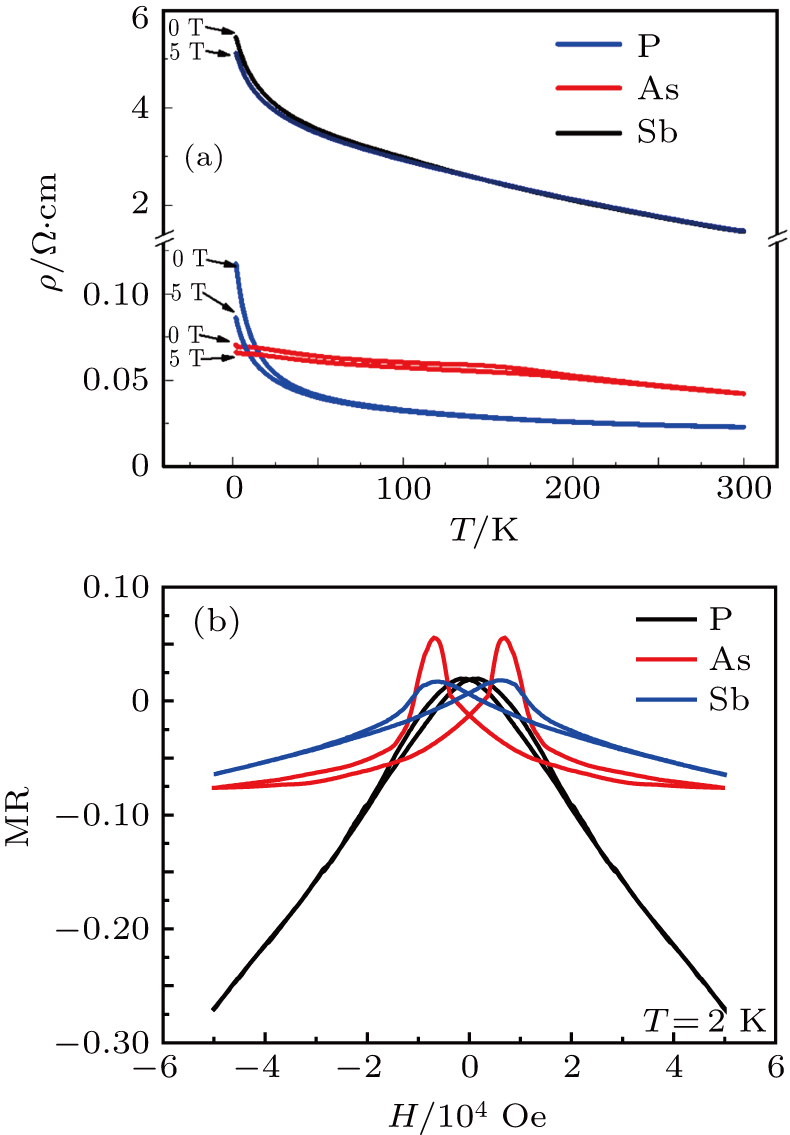 | Fig. 3. (a) (Ba0.7K0.3)(Zn0.85Mn0.15)2(As1−yPny)2 (Pn = Sb and P; y = 0.1) samples’ temperature dependent resistivity. (b) Field dependent resistivity of the samples in panel (a) at 5 K. |
All three samples show negative magnetoresistance (MR) at low temperature regions. As shown in Fig. 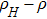
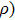
In DMS, ferromagnetic ordering is mediated by carriers. Thus Hall effect was measured to probe possible change upon Sb- or P- doping. Figure 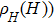
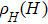
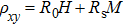
 | Fig. 4. (Ba0.7K0.3)(Zn0.85Mn0.15)2(As1−yPny)2 (Pn = Sb, As, and P; y = 0.1) samples’ field dependent Hall resistivity at (a) 2 K, (b) 50 K, and (c) 100 K. |
| Table 1.
The hole concentrations (in units of 1020 cm−3) of (Ba0.7K0.3)(Zn0.85Mn0.15)2(As1−yPny)2 for y=0.1 . . |
Studies of external pressure-effects on BZA revealed suppression of Curie temperature upon compression. Iso-valent substitution of Sb or P into As in BZA to produce chemical pressure is an attractive attempt to tune the magnetic properties because previous studies on physical pressure-effects on BZA have revealed the suppression of Curie temperature upon compression. Although lattice extension does not increase TC as expected, the change of resistivity with modification of cell volume has been reproduced. Nevertheless, the large MR effect induced by P-doping offers a new boulevard to improve magnetoelectric properties for spintronic materials.
Authors are grateful for the discussion with Maekawa S.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] |