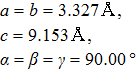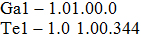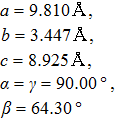Cite this Article
Wang Youchun, Tian Fubo, Li Da, Duan Defang, Xie Hui, Liu Bingbing, Zhou Qiang, Cui Tian. Structural and electrical properties of Ga–Te systems under high pressure. Chinese Physics B, 2019, 28(5): 056104  
Permissions
Structural and electrical properties of Ga–Te systems under high pressure
Wang Youchun, Tian Fubo †, Li Da, Duan Defang, Xie Hui, Liu Bingbing, Zhou Qiang, Cui Tian ‡
State Key Laboratory of Superhard Materials, College of Physics, Jilin University, Changchun 130012, China

 

† Corresponding author. E-mail: tianfb@jlu.edu.cn cuitian@jlu.edu.cn

Abstract
Abstract

First-principles evolutionary calculation was performed to search for all probable stable Ga–Te compounds at extreme pressure. In addition to the well-known structures of P63/mmc and Fm-3m GaTe and I4/m Ga2Te5, several new structures were uncovered at high pressure, namely, orthorhombic I4/mmm GaTe2 and monoclinic C2/m GaTe3, and all the Ga–Te structures stabilize up to a maximum pressure of 80 GPa. The calculation of the electronic energy band indicated that the high-pressure phases of the Ga–Te system are metallic, whereas the low-pressure phases are semiconductors. The electronic localization functions (ELFs) of the Ga–Te system were also calculated to explore the bond characteristics. The results showed that a covalent bond is formed at low pressure, however, this bond disappears at high pressure, and an ionic bond is formed at extreme pressure.

PACS: 61.50.Ah;64.60.-i;71.15.Mb
Keyword:density functional theory;Ga-Te system;electronic property
1. Introduction

Semiconductor materials from the III–IV families, such as GaTe and Ga2Te3, are of special interest because of their potential applications in solid-state batteries,[1] radiation detectors, thermoelectric devices, and optoelectronics.[2–4] Previous studies[5–7] on the phase diagram showed the existence of GaTe and Ga2Te3. Other compounds were also reported in various investigations. For example, Ga3Te2 and GaTe3 were proposed by Newman et al.,[6] Lissauskas and Yasutis[8] presented Ga3Te4, Ga2Te5 was proposed by Alapini et al.[9] We found in literature investigation that most studies focused on GaTe and Ga2Te3.

GaTe is a layer conductor with a bandgap of 1.65 eV reported by Brebner[10] or 1.7 eV report by Yamamoto[11] at room temperature. Shenoy et al.[12] reported that GaTe can crystallize in hexagonal (P63/mmc) and monoclinic (C2/m) structures. The two structures are composed of two layers of Te–Ga–Ga–Te with 8 and 12 atoms per unit cell. The difference between the two structures is that only two-thirds of the Ga–Ga dimers are oriented perpendicular to the layers, whereas the remaining one-third lay nearly on the plane of the layer in C2/m GaTe. Shenoy et al.[12] determined that the P63/mmc and C2/m GaTe are indirect and direct band gap semiconductors, respectively. They also synthesized C2/m GaTe, which is regarded as a stable structure at ambient pressure. Yamamoto et al.[11] and Zubiaga et al.[13] reported that the intra-layer bonds of C2/m GaTe are mostly covalent with some ionic contributions, whereas its inter-layer bonds are weak van der Waals type. Schwarz et al.[14] indicated that C2/m GaTe will transform to the Fm-3m phase at 10 GPa, however, this structure is metastable.

Ga2Te3 is a zinc blende structure, in which one-third of the cation sites are vacant.[15,16] Huang[15] and Newman[17] stated that the exact structure of vacancy-ordered Ga2Te3 is unknown, however, two types of short-range order zinc blende structures (i.e., mono-Ga2Te3 and ortho-Ga2Te3) exist. Regardless of the structure, Shchennikov et al.[18] proposed that the bond between Ga and Te atoms is covalent sp3 bond. Guizzetti et al.[19] and Zhu et al.[20] calculated the band structure of Ga2Te3, which was found to be direct. Huang et al.[15] determined that the bandgaps of both mono-Ga2Te3 and ortho-Ga2Te3 structures were indirect using PBE and HSE06 (PBE). The electronic properties of the high-pressure phase were investigated by Shchennikov et al.[18] They found that a semiconductor–metal phase transition occurs while transforming from a zinc blende structure to a Bi2Te3-type structure at 4.4 GPa.

To the best of our knowledge, the Ga–Te system exhibits abundant stoichiometric ratio and exotic physical and chemical properties. Although Ga–Te compounds have been studied for decades, a detailed theoretical research of their phase equilibria and electronic, dynamic, and mechanical properties can help solve controversies and possibly predict new technologically useful materials.

2. Computational methods

The high pressure crystal structures of Ga–Te system were explored by the evolutionary algorithm method[21–28] as implemented in the universal structure predictor: evolutionary xtallography (USPEX) code, which has been successfully applied to a variety of systems. USPEX was interfaced with many ab initio codes, such as Vienna ab initio simulation package (VASP),[29] Cambridge sequential total energy package (CASTEP),[30,31] and so on. Brillouin zone (BZ) sampling using a grid of spacing of 2π ×0.05 Å−1 and a plane-wave basis set cutoff of 400 eV was sufficient for the initial search over structures. We studied systems containing up to 16 atoms per unit cell. The first generation of structures were generated randomly. All structures were relaxed at 0 K and the enthalpy was used as fitness. The energetically worst structures (40%) were discarded and a new generation evolved from the remaining structures. The best structure of one generation was carried over into the next generation. We generally terminated the runs after 60 generations, and all runs had found the minimum-enthalpy structures much earlier. Our calculations on the Ga–Te system were mainly performed with the VASP code using the plane-wave pseudopotential method[32] and employing the Perdew–Burke–Ernzerhof approach (PBE)[33] of the generalized gradient approximation functional (GGA).[34] The plane-wave basis-set cutoff energy was set to 750 eV, and appropriate Monkhorst–Pack k-meshes[35] were employed with a resolution of 2π ×0.03 Å−1 for BZ sampling to ensure that all the enthalpy calculations were converged to less than 1 meV per atom. The lattice dynamical properties were calculated based on a supercell approach as implemented in the PHONOPY package.[36] All calculations were performed using a 2 ×2 ×2 supercell of 96 atoms for I4/mmm GaTe2, 128 atoms for C2/m GaTe3, and 56 atoms for I4/m Ga2Te5. The hybrid function of Heyd, Scuseria, and Ernzerhof (HSE06)[37,38] was also used to verify the results of band structures with the PBE function. The HSE method was performed in the PWmat code,[39,40] which has been proved to be accurate and efficient to calculate large semiconductor systems.

3. Results and discussion
3.1. Crystal structures and stability of Ga–Te systems

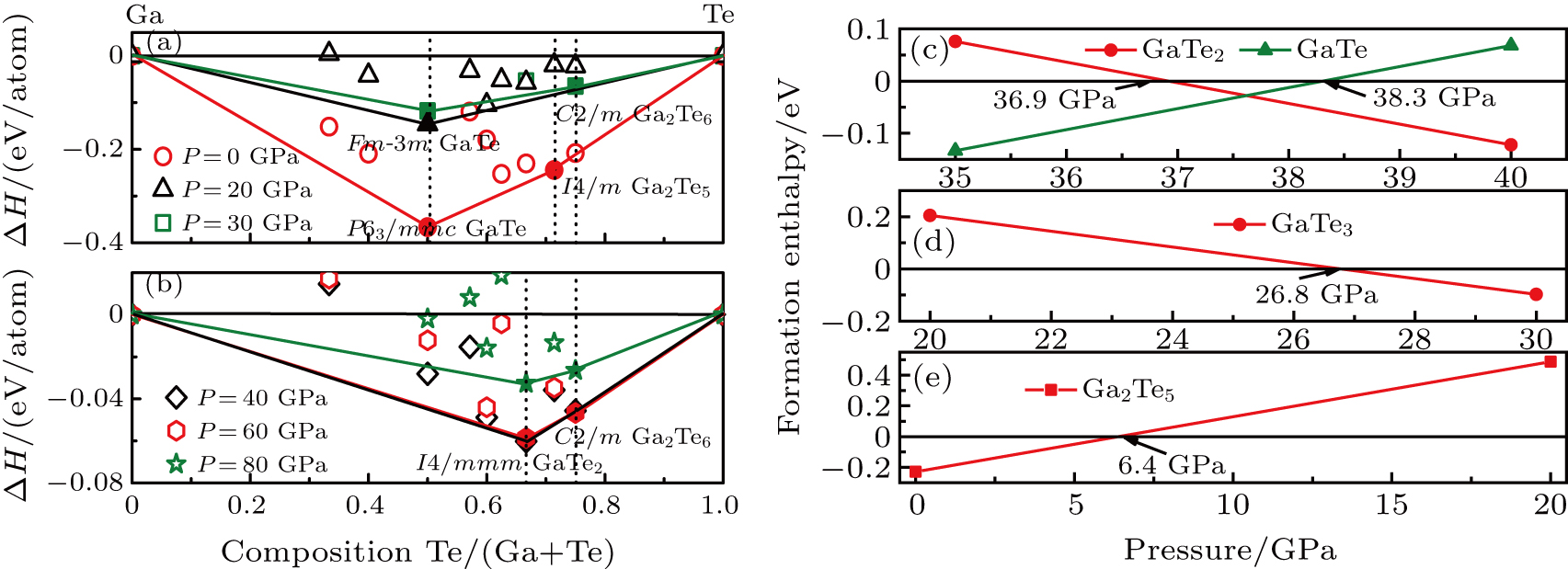
The thermodynamics of the Ga–Te system can be visualized by depicting the thermodynamic convex hull, which is presented in Fig. 1. A thermodynamically stable structure can be synthesized in principle.[41] Figures 1(a) and 1(b) show the absence of Ga2Te3. It can be seen from Fig. 1(a) that P63/mmc GaTe and I4/m Ga2Te5 coexist under normal conditions. With increasing pressure, we uncovered two new structures GaTe2 and GaTe3 at 40 GPa and 30 GPa and observed the disappearance of GaTe at 40 GPa. In order to determine the stable pressure range of each structure, the formation enthalpies of GaTe, GaTe2, and GaTe3 are calculated and presented in Figs. 1(c) and 1(d). From Figs. 1(c) and 1(d), we noticed that GaTe2 and GaTe3 are thermodynamically stable above 36.9 GPa and 26.8 GPa because of their negative formation enthalpies, and GaTe and Ga2Te5 have positive formation enthalpies above 38.3 GPa and 6.4 GPa, respectively. Detailed enthalpy calculations for the most stable structures allowed us to reconstruct the P–x phase diagram of the Ga–Te system (Fig. 2). Interestingly, we found that GaTe, has a hexagonal (P63/mmc) structure under ambient condition in our calculations. This result is inconsistent with an earlier statement.[11] The minor discrepancy may be attributed to the disregard of temperature effects in our calculations. Therefore, we considered C2/m GaTe a metastable structure at 0 K. As pressure increases, it was proposed to transform from the P63/mmc phase into the cubic Fm-3m structure at 6.9 GPa (Fig. 2). This result slightly varies from that proposed by Schwarz et al. (i.e., C2/m structure changes to Fm-3m phase). Subsequently, GaTe is observed to be unstable above 38.3 GPa. GaTe2 and GaTe3 are determined to adopt the I4/mmm and C2/m structures above 36.9 GPa and 26.8 GPa, respectively. Ga2Te5 is stable with a tetragonal structure (I4/m phase) in a pressure range of 0–6.4 GPa. Notably, we found that stabilizing the Ga–Te system up to at least 80 GPa is difficult.

Fig. 1. Thermal stability of gallium tellurium compounds. (a) and (b) Convex hull diagrams for Ga–Te system at 0 GPa, 20 GPa, 30 GPa, 40 GPa, 60 GPa, and 80 GPa, respectively. (c)–(e) The formation enthalpy of GaTe, GaTe2, GaTe3, and Ga2Te5.
Fig. 2. Pressure–composition phase diagram of the Ga–Te system.

The Ga–Te system is known to possess abundant stoichiometry, and we searched for candidate high-pressure structures of the Ga–Te system with 2, 4, and 8 units per cell (f.u./cell) at a pressure range of 0–150 GPa. Calculating the structural properties is a crucial step to understanding the characteristics of materials from a microscopic point of view. In addition to the known structures, i.e., P63/mmc and Fm-3m GaTe and I4/m Ga2Te5, a group of new structures were discovered at high pressure, namely, orthorhombic I4/mmm GaTe2 (2 f.u./cell) and monoclinic C2/m GaTe3 (4 f.u./cell) as shown in Fig. 3. The lattice parameters and atomic positions are listed in Table 1. Figure 3(a) illustrates that I4/mmm GaTe2 (eightfold coordination) has a layered structure, and Ga atoms link with eight Te atoms. The Ga atom located at the center position forms a regular hexahedron with the eight surrounding Te atoms. Seeburrun et al.[42] proposed that a cyclic structure (molecular structure) for GaTe2 is the lowest energy structure based on density functional theory and Møller–Plesset second-order perturbation theory. We found that the bond distance of Ga–Te for I4/mmm GaTe2 is equal to the cyclic structure by disregarding the influence of pressure. For C2/m GaTe3 (Fig. 3(b)), the Ga atom also connects with the eight surrounding Te atoms to form a regular hexahedron.

Fig. 3. The selected stable structures of Ga–Te compounds: (a) I4/mmm GaTe2 at 60 GPa, (b) C2/m GaTe3 at 60 GPa. The red and purple balls represent the Ga and Te atoms, respectively.
Table 1.

Lattice parameters and atomic positions of I4/mmm GaTe2 and C2/m GaTe3.

.

The phonon dispersion curves were calculated at 60 GPa and 0 K, as shown in Fig. 4, to examine the stability of I4/mmm GaTe2 and C2/m GaTe3, respectively. This figure clearly indicates the absence of any imaginary frequency in the entire BZ, which verifies the dynamic stability of the two phases. Nassary et al.[43] researched I4/m Ga2Te5 based on experiment. However, a detailed description of theoretical studies remains lacking. Therefore, we also calculated the phonon frequency of I4/m Ga2Te5 as shown in Fig. 4(c). This figure shows the absence of any imaginary frequency, thereby indicating that the phase is dynamically stable.

Fig. 4. The phonon band structures for Ga–Te compounds: (a) I4/mmm GaTe2, (b) C2/m GaTe3, (c) I4/m Ga2Te5.

Mechanical stability is a necessary condition for the existence of crystal. Elastic constants can provide important information for the stability of materials. In this study, we calculated the elastic constants of Fm-3m GaTe, I4/mmm GaTe2, C2/m GaTe3, and I4/m Ga2Te5 using the strain-stress method at 20 GPa, 60 GPa, 60 GPa, and 0 GPa, respectively. The calculated results are listed in Table 2. The elastic constants Cij clearly satisfy the traditional mechanical stability conditions for the four structures, thereby indicating their mechanical stability.

Table 2.

Elastic constants Cij (in kbar) for Fm-3m GaTe, I4/mmm GaTe2, C2/m GaTe3, and I4/m Ga2Te5 at 20 GPa, 60 GPa, 60 GPa, and 0 GPa, respectively.

.
3.2. Electronic properties of Ga–Te systems

We presented an extensive study of the electronic properties of Fm-3m GaTe, I4/mmm GaTe2, C2/m GaTe3, and I4/m Ga2Te5 along high-symmetry directions in the first Brillouin zone. The selected electronic band structures are displayed in Fig. 5. Figure 5(a) shows that there are several bands crossing at the Fermi level and indicates that GaTe becomes metallization at high pressure. It can be seen from Figs. 5(b) and 5(c) that there are more bands crossing at the Fermi level and the two structures are also metallized at extreme pressure. Interestingly, we found that as the Te content increases, the number of energy bands crossing at the Fermi surface increases. This indicates that Te accounts for the main contribution near the Fermi surface. Nassary et al.[43] had synthesized Ga2Te5 single crystal by a special modified Bridgman technique and measured the Hall coefficient, they concluded that Ga2Te5 is a layered semiconductor. In this study, we also calculated the electronic band structure (Fig. 5(d)) using the HSE06 potential, which indicates that Ga2Te5 is a semiconductor with an indirect band gap of 1.465 eV. The Ga–Te system is evidently in semiconductor state under ambient condition and becomes metallized at extreme pressure.

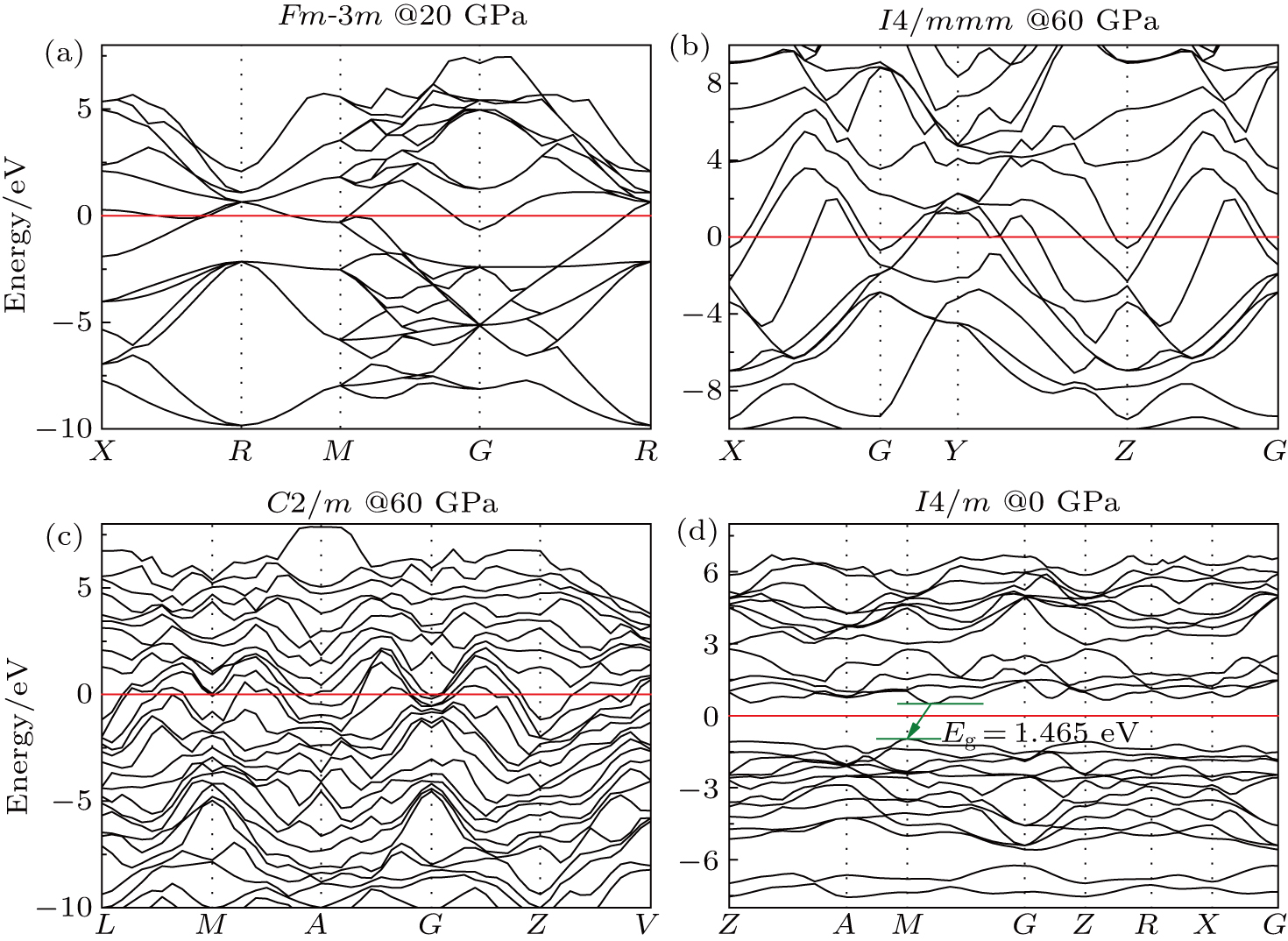Fig. 5. Electronic band structures of (a) Fm-3m GaTe, (b) I4/mmm GaTe2, (c) C2/m GaTe3, (d) I4/m Ga2Te5.

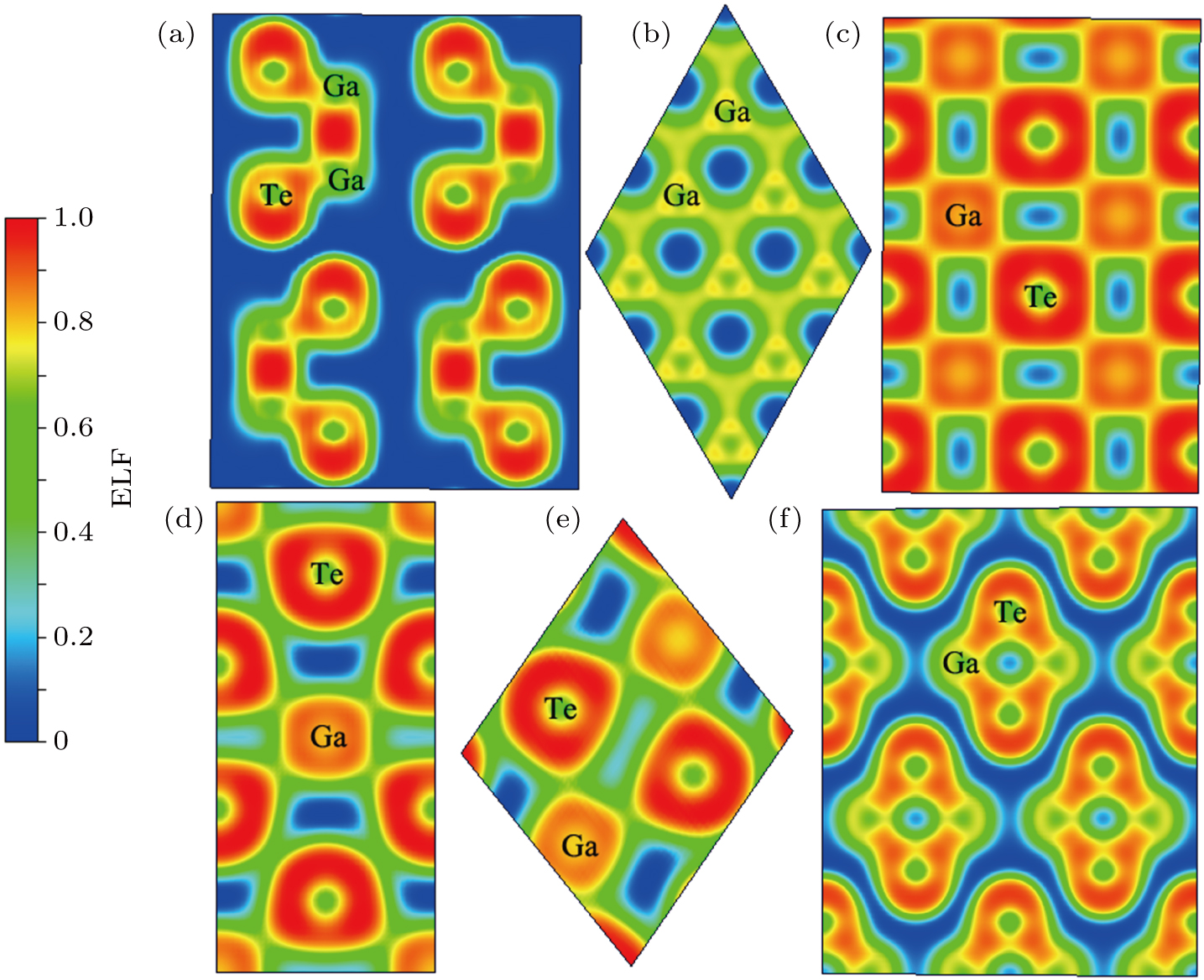
In order to understand the reasons for this phenomenon, we calculated electronic localization function (ELF), which offers a reliable measure for electron pairing and localization to visualize the nature of the bonding characteristic of the Ga–Te system. The ELF values of P63/mmc and Fm-3m GaTe, I4/mmm GaTe2, C2/m GaTe3, and I4/m Ga2Te5 are presented in Fig. 6. As shown in Fig. 6(a), the bonds with the layer for P63/mmc GaTe are mostly covalent, and weak van der Waals forces exist between the interlayer (Fig. 6(b)). In Fig. 6(c), the covalent bond between Ga and Te atoms is weakened, whereas the ionic bond is enhanced. Figures 6(d) and 6(e) clearly show that the two high-pressure phases have ionic bonds between Ga and Te atoms. Figure 6(f) also illustrates that covalent bonds are formed between Ga and Te atoms. Notably, covalent bonds are observed in the Ga–Te system at low pressure. However, these covalent bonds disappear upon compression, and the ionic bonds are formed in the Ga–Te system at extreme pressure.

Fig. 6. Electron localization function maps in the planes where the gallium and tellurium atoms lie: (a) P63/mmc GaTe on the (110) plane at 0 GPa, (b) P63/mmc GaTe on the (001) plane at 0 GPa, (c) Fm-3m GaTe on the (11–1) plane at 20 GPa, (d) I4/mmm GaTe2 on the (0-10) plane at 60 GPa, (e) C2/m GaTe3 on the (31, 63, –1) plane at 60 GPa. (f) I4/m Ga2Te5 on the (48, –48, –1) plane at 0 GPa.

To discuss the situation further, the atoms in molecules method (Bader charge analysis)[44] was performed to evaluate charge transfer. The number of electrons in the Ga–Te system is listed in Table 3, which shows that a Te atom acquires considerably fewer electrons in the three high-pressure phases. This finding indicates that the sharing of electrons between Ga and Te atoms decreases, and ionic bonds with electrostatic interaction begin to form. Therefore, we deduced that the Ga–Te system can be ionized at certain pressures when energy is low, which promotes the stability of the structure.

Table 3.

The Bader charge analysis for the Ga–Te system.

.

In addition, when the structure is a semiconductor, the primary contribution in the system is covalent bonds, when the system is metallized, the major contribution is ionic bonds. This finding can be attributed to the ionization of the system and the gradual increase in the number of free electrons, which produce the metallic characteristics of the system. The electron characteristics of the Ga–Te system are unified at the microscale and macroscale.

4. Conclusion

In summary, the candidate high-pressure crystal structures of the Ga–Te system were identified using the evolutionary algorithm of universal structure predictor: evolutionary xtallography code, at pressures below 150 GPa. Several novel phases were discovered (i.e., I4/mmm GaTe2 and C2/m GaTe3) at high pressure. The thermodynamic properties of the Ga–Te system were investigated using first-principles theory. The results showed that all the structures mentioned in this paper become thermodynamically unstable at pressures higher than 80 GPa. In addition, we deduced that P63/mmc GaTe is more thermodynamically stable than C2/m GaTe under ambient condition and this structure transforms into the Fm-3m phase at 6.9 GPa. The two novel structures, I4/mmm GaTe2 and C2/m GaTe3, are stable above 36.9 GPa and 26.8 GPa, respectively. The I4/m Ga2Te5 is stable between 0 and 6.4 GPa. The calculations of the electronic energy band indicate that the high-pressure phases of the Ga–Te system are metallic, whereas the low-pressure phases are semiconductors. We also calculated the ELF of the Ga–Te system to further explore the bond characteristic. The results indicated the formation of a covalent bond at low pressure, which disappears at high pressure.

Reference
[1] Balkanski M Julien C Emery J Y 1989 J. Power Sources 26 615
[2] Sen S Bose D N 1984 Solid. State. Commun. 50 39
[3] Hu P Zhang J Yoon M Qiao X Zhang X Wei F Tan P Zheng W Liu J Wang X Idrobo C Geohegan D Xia O K 2014 Nano Res. 7 694
[4] Bose D N Pal S 2001 Phys. Rev. 63 235321
[5] Klemm W Vogel H U 1934 Z. Anorg Allg. Chem. 219 45
[6] Newman P C Brice J C Wright H C 1961 Philips. Res. Reps. 16 41
[7] Antonopoulos J G Karakostas T Bleris G L 1981 J. Mater. Sci. 16 733
[8] Lisauskas V S Yasutis V V 1972 Litov. Fiz. Sb. SSSR 12 1019
[9] Alapini F Flahaut J Guittard M Jaulmes S Julien-Pouzol M 1979 J. Solid State. Chem. 28 309
[10] Brebner J L Fischer G Mooser E 1962 J. Phys. Chem. Solids 23 1417
[11] Yamamoto A Syouji A Goto T Kulatov E Ohno K Kawazoe Y Uchida K Miura N 2001 Phys. Rev. 64 035210
[12] Shenoy U S Gupta U Narang D S 2016 Chem. Phys. Lett. 651 148
[13] Zubiaga A Garcıa J A Plazaola F 2002 J. Appl. Phys. 92 7330
[14] Schwarz U Syassen K Kniep R 1995 J. Alloy. Compd. 224 212
[15] Huang G Y Abdul-Jabbar N M Wirth B D 2014 Acta Mater. 71 349
[16] Al-Orainy R H Nagat A T Hussein S A Ebnalwaled A A 2015 International Research Journal of Engineering and Technology (IRJET) 2 816
[17] Newman P C 1962 J. Phys. Chem. Solids 23 19
[18] Shchennikov V V Savchenko K V Popova S V 2000 Phys. Solid. State. 42 1036
[19] Guizzetti G Meloni F 1982 Il. Nuovo. Cimento. 1 503
[20] Zhu H Yin J Xia Y 2010 Appl. Phys. Lett. 97 083504
[21] Oganov A R Glass C W 2006 J. Chem. Phys. 124 244704
[22] Glass C W Oganov A R Hansen N 2006 Comput. Phys. Commun. 175 713
[23] Oganov A R Glass C W Ono S 2006 Earth. Planet. Sci. Lett. 241 95
[24] Lyakhov A O Oganov A R Valle M 2010 Comput. Phys. Commun. 181 1623
[25] Oganov A R Lyakhov A O Valle M 2011 Accounts Chem. Res. 44 227
[26] Lyakhov A O Oganov A R Stokes H T 2013 Comput. Phys. Commun. 184 1172
[27] Duan D F Liu Y X Tian F B 2015 Sci. Rep. 4 6968
[28] Duan D F Huang X L Tian F B 2015 Phys. Rev. 91 180502
[29] Kresse G Furthmüller J 1996 Comput. Mater. Sci. 6 15
[30] Segall M D Lindan P J D Probert M J Pickar C J Hasnip P J Clark S J Payne M C 2002 J. Phys. Condens. Matter 14 2717
[31] Clark S J Segall M D Pickard C J Hasnip P J Probert M I J Refson K Payne M C 2005 Z. Kristallogr.-Cryst. Mater 220 567
[32] Vanderbilt D 1990 Phys. Rev. 41 7892
[33] Hammer B Hansen L B Norskov J K 1999 Phys. Rev. 59 7413
[34] Perdew J P Burke K Ernzerhof M 1996 Phys. Rev. Lett. 77 3865
[35] Monkhorst H J Pack J D 1976 Phys. Rev. 13 5188
[36] Togo A Oba F Tanaka I 2008 Phys. Rev. 78 134106
[37] Krukau A V Vydrov O A Izmaylov A F Scuseria G E 2006 J. Chem. Phys. 125 224106
[38] Heyd J Scuseria G E Ernzerhof M 2003 J. Chem. Phys. 118 8207
[39] Jia W L Cao Z Y Wang L Fu J Y Chi X B Gao W G Wang L W 2013 Comput. Phys. Commun. 184 9
[40] Jia W L Fu J Y Cao Z Y Wang L Chi X B Gao W G Wang L W 2013 J. Comput. Phys. 251 102
[41] Ghosh G van de Walle A Asta M 2008 Acta Mater. 56 3202
[42] Seeburrun N Alswaidan I A Fun H K A 2015 RSC. Adv. 5 68076
[43] Nassary M M Gerges M K Shaban H T 2003 Phys. 337 130
[44] Bader R F W 1990 Atoms Molecules A Quantum Theory Clarendon Oxford