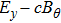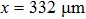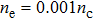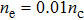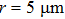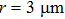Laser-driven wakefield acceleration (LWFA) is one of the most promising schemes for achieving compact and affordable accelerators, providing large accelerating gradient orders of magnitude higher than those available in conventional radio-frequency accelerators.^[1] Therefore, charged particle acceleration in the laser–plasma interactions has attracted great interest since the LWFA mechanism was first proposed by Tajima and Dawson in 1979.^[2] Thanks to the development of high-power laser technologies, significant progress has been made in 2004 when the quasi-monoenergetic electron bunches were first obtained in experiments.^[3–5] Recently, electron bunches with the energy up to 4.2 GeV have been generated in a 9-cm plasma waveguide using a 40-fs laser pulse with 16-J energy.^[6] These significant experimental results were obtained in the bubble regime when a short intense laser pulse almost expels electrons completely from the first half of the plasma wave. The longitudinal electric field in the cavitated region is uniform in the transverse direction and linear in propagation axis so that the self-injected electron bunch with duration less than about 10 fs can get monoenergetic.^[7] These electron bunches have a lot of potential applications such as generation of X and γ rays,^[8–10] ultrafast imaging,^[11] cancer therapy,^[12] radiotherapy,^[13] etc.

Although there have been many theoretical and numerical investigations of LWFA and the scaling laws have also been found,^[14–18] to obtain high-quality electron bunches in practical experiments is a challenging task due to the complexity of the strongly nonlinear bubble regime. As we know, the laser pulse interacts with plasma electrons at the very front and the major part of the laser pulse propagates freely in the blow-out region. Thus, the pulse tail gradually overtakes its head, where an optical shock is formed and the pulse etches back.^[16] All these lead to the pulse shortening and faster dephasing, which in turn decreases slowly the group velocity of the laser pulse. Consequently, the self-injected electron bunch will run into the decelerating phase of the bubble to limit the maximum energy gain and enlarge the energy spread. At the same time, these relativistic self-injected electrons can easily come into betatron resonance because of the transverse focusing field in the bubble regime. Thus, it will blow up the electron bunch emittance and increase divergence.^[9]

Numerous methods have been proposed to optimize the quality of the self-injected electron bunch and improve its stability, such as pulse colliding injection,^[19] ionization-induced injection,^[20–23] density transition injection,^[24,25] guiding of the laser pulse in a performed parabolic^[6,26,27] or hollow channel,^[28] etc. Among those, the hollow plasma channel is considered as an efficient way to overcome the drawbacks in the uniform plasma and significantly optimize the electron acceleration. The lack of ion cavity in the hollow plasma channel is favorable to increase the effective phase velocity of the bubble and the dephasing length and reduce remarkably the focusing force acting on the electrons in the bubble regime. It is very important for electron acceleration to tunable control in experiments. The parameters of the hollow plasma channel can provide independently control over the focusing and accelerating field in the channel.^[29] Recently Pukhov et al. derived scaling laws for deep plasma channel with a zero density on axis driven by ultrashort pancake-like laser pulses and observed a witness beam with energy up to 7.5 GeV and only 0.3% total energy spread in numerical simultions.^[28] Further, Thomas et al. obtained the generalization of the bubble theory for a radially inhomogeneous plasma and it can predict the shortening and steepening of the bubble.^[30] Yi et al. used the hollow plasma channel to overcome the defocusing of the positively charged witness beam in the bubble regime and accelerate the latter up to 4-TeV energy with low emittance.^[31,32] However, high-quality witness bunches in these schemes should be injected externally into the bubble regime. It requires such bunches with energy GeV or TeV level must be generated from conventional radio-frequency accelerator.^[19] Recently the first experimental demonstration of creating an extended hollow plasma channel is encouraging for undertaking future the generation of high-quality electron bunch at intense laser facilities.^[33]

In this paper, we focus on the self-injection and acceleration of electron in the bubble regime of the hollow plasma channel driven by the Guassian-shaped laser pulses, which are used commonly in worldwide experiments. By optimizing the parameters of laser pulse and hollow plasma channel, it finds that when the radius of the hollow plasma channle matches the spot size of the laser pulse in a rarefied plasma, electrons from the bubble sheath can be self-injected into the rear of the bubble. The dynamics of the electrons in the whole interaction process will be discussed. The focusing field is almost zero in the hollow plasma channel, while it is strong around the periphery of the hollow plasma channel in the bubble regime. Self-injected electrons can be confined in the channel and are quasi-phase-stably accelerated in the rear of the bubble, where the accelerating electric field is uniform transversely and flatten in propagating direction. Therefore, a self-injection electron bunch with low energy spread and divergence can preserve a steady state in the whole laser–plasma interactions without obvious quality degradation.

We carried out two-dimensional (2D) particle-in-cell (PIC) simulations using VORPAL code to demonstrate electron self-injection and acceleration in hollow plasma channels driven by laser pulses.^[34] In order to comparison with the existing results,^[15] we choose the same laser parameters as in the latter. In the simulations, a bi-Gaussian laser pulse is irradiated into a hollow plasma channel from the left boundary (x = 0). The pulse envelope is , where the full-width-half-maximum (FWHM) of the laser intensity is , y is the transverse direction, the pulse duration is , and the wave length is . The laser normalized vector potential is , which corresponds to the intensity of I=2.1 ×10²⁰ W/cm², where c is the speed of light in vacuum and is the laser frequency, e and m are the electron charge and mass, respectively. The laser pulse propagates along the x axis and is linearly polarized in z axis. The hollow plasma channel has a plasma density of the form n(r) = 0 for and for , where n_e is the electron plasma density in the wall, is the radial distance from the axis and r₀ is the hollow channel radius. The radius of the channel hollow should be chosen to let the laser pulse propagate freely without pulse shortening and optical shock around the propagation axis. The transverse ponderomotive force of the laser pulse near the channel wall should be very strong. Thus, we set the radius of the hollow channel to be slightly smaller than the spot size of the laser pulse, which allows sufficient electrons in the channel wall to move into the bubble sheath. We have scanned over a range of the channel radii and found that a radius provides the best performance. The plasma with density initially locates in a region between and . The simulation box is featured as , and the grid size is set as λ/30 along the x axis and λ/40 on the y axis. Ten particles are put in each cell and the mass ratio between the ion and the electron is set as 1836. The transverse and longitudinal boundary conditions are periodic and absorbing, respectively. The initial electron and ion temperatures are assumed to be so small that their effects can be ignored. In addition, because our simulations are 2D spatial, the electron numbers will be given with an unit of in the z axis.

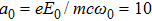
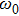
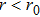
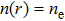
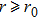
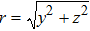
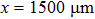
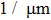
Figure 1 shows the electron density distributions of the laser–plasma interaction at t = 0.5 ps, 1.23 ps, 3.5 ps, and 5.2 ps, respectively. The dashed lines show the boundaries of the hollow plasma channel. Simulation results indicate that there are roughly three stages of electron acceleration: (i) electron self-injection stage, (ii) electron oscillation stage, and (iii) electron-quasi phase-stable acceleration stage. In the electron self-injection stage before t = 0.6 ps, as shown in Fig. 1(a), the background electrons located near the edge of the channel are expelled by the laser ponderomotive force, generating a series of wake bubbles behind the laser pulse. The expelled electrons with high energy cannot be confined in the bubble sheath and their transverse outflow forms a bow wave at the front of the bubble. A small fraction of sheath electrons can be self-injected into the rear of the first bubble. Due to the lack of focusing force in the hollow plasma channel, the self-injected electrons move transversally toward the wall of the hollow plasma channel. Then the major characteristic of self-injected electron dynamics is transverse oscillation between the upper and lower edges of the hollow plasma channel. Some self-injected electrons with high transverse velocity can escape from the edge of the hollow plasma channel, while the rest self-injected electrons reverse their signs of transverse velocities near the edge of the hollow plasma channel and are confined between the upper and lower edges of the hollow plasma channel. Figure 1(b) shows that most of self-injected electrons are reflected secondly from the edges of the hollow plasma channel and a minority of self-injected electrons located in the bunch tail is dispersed outside the channel. Eventually, a wide electron bunch almost without electron escaping after about t = 2.4 ps is formed in the bottom of the first bubble. In the electron quasi-phase-stable acceleration stage, without laser pulse shortening and optical shock in the hollow channel, the effective bubble phase velocity increases in the hollow plasma channel compared that in a uniform plasma. The self-injected electron bunch always stays close to the rear of the first bubble as shown in Fig. 1(c). In this stage, the laser depletion length is longer than the electron dephasing length. Therefore, the self-injected electron bunch can be quasi-phase-stably accelerated forward with the laser pulse for a long distance till out of the plasma slab as shown in Fig. 1(d).

Fig. 1.

	Figure Option ViewDownloadNew Window
	Fig. 1. Electron density distributions at t = 0.5 ps (a), 1.23 ps (b), 3.5 ps (c), and 5.2 ps (d), respectively. The electron density is normalized by the background plasma density. The dashed lines show the boundaries of the hollow plasma channel.

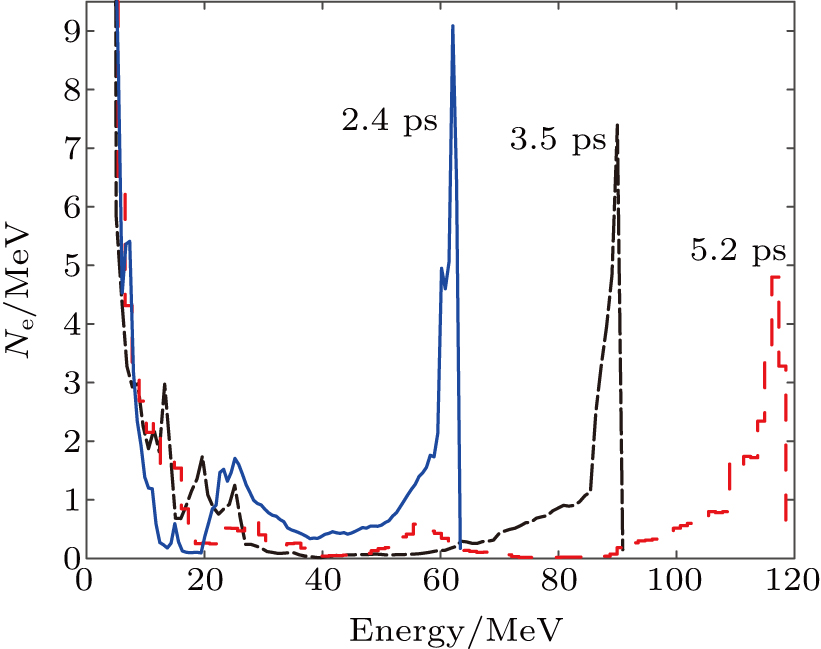
It is very important to analyze the quality of the self-injected electron bunch in our scenario. The self-injected bunch is accelerated to 117 MeV of the peak energy with 2.9% energy spread at t = 5.2 ps when it moves out of the plasma slab, as shown in Fig. 2. It contains about 3.7 ×10⁹ electrons and has longitudinal and transverse sizes of about and , respectively. Compared to the uniform plasma case as shown in Fig. 6, the wide electron bunch stays monoenergetic for a long time of acceleration since it is formed near the bottom of the bubble. It is because that the laser depletion length is longer than the electron dephasing length in the hollow plasma channel. Figure 3 shows the divergence angle distributions of the electrons at different time corresponding to that in Fig. 1. It indicates that the divergence angle is very large during the stages of electron self-injection and oscillation as shown in Figs. 3(a) and 3(b). However, the divergence angle in the electron quasi phase-stable acceleration stage reduces remarkably to about ±2° at t = 3.5 ps and ±1.5° at t = 5.2 ps as shown in Figs. 3(c) and 3(d). It is because that the self-injected electron bunch is confined in the channel and continually accelerated forward with the laser pulse.

Fig. 2.

	Figure Option ViewDownloadNew Window
	Fig. 2. The energy spectra of electrons at t = 2.4 ps, 3.5 ps, and 5.2 ps, respectively.

Fig. 3.

	Figure Option ViewDownloadNew Window
	Fig. 3. The energy distribution of electrons as a function of the divergence angle at t= 0.5 ps (a), 1.23 ps (b), 3.5 ps (c), and 5.2 ps (d), respectively. The electron density is in arbitrary unit.

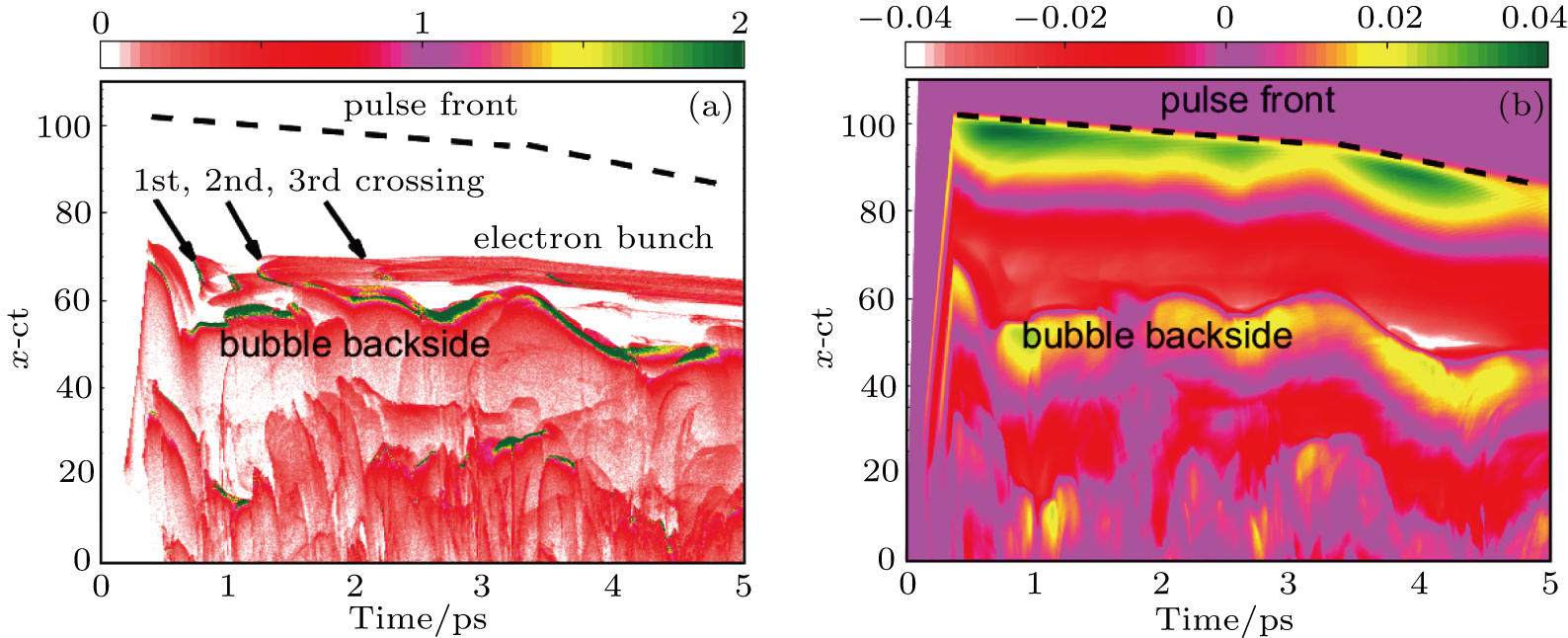
In order to further investigate the generation of the high-quality electron bunch in the hollow plasma channel, we presented the spatial distributions of transverse focusing field and longitudinal accelerating field E_x at t = 1.23 ps in Figs. 4(a) and 4(b), respectively. In Fig. 4(a), the dashed lines indicate the boundaries of the hollow plasma channel and the solid line shows the transverse distribution of the focusing field at . One can see that the transverse focusing field in the bubble region is almost zero in the hollow plasma channel, while it increase linearly along y axis from zero at the channel boundary to the maximum at the bubble sheath and then decrease to zero rapidly. The self-injected electrons with transverse velocity would be reflected by the strong focusing force and confined in the hollow plasma channel as a wide bunch as shown the rectangle marked by the dot–dashed lines. Other self-injected electrons behind the wide bunch in the rear of the bubble as shown in Fig. 1(b) will escape from the hollow plasma channel because there is no confining potential well in the peripheral region around the channel. The longitudinal electric field E_x experienced by the wide electron bunch is transversely uniform as shown in Fig. 4(b). Furthermore, Figure 4(c) shows the transverse distributions of the longitudinal electric field in the center of the self-injected electron bunch at t = 0.5 ps, 2 ps, 3 ps and 5 ps, respectively. It proves that the longitudinal electric field is transversely uniform for the whole acceleration process. The longitudinal on-axis electric field of the wide electron bunch is nearly flat after the electron self-injection stage as show in Fig. 4(d), where the black rectangle represents the location of the self-injected electron bunch. Thus, the transverse focusing and longitudinal accelerating fields are ideal to accelerate the self-injected electron bunch monoenergetically for a long distance.

Fig. 4.

Figure Option ViewDownloadNew Window

Fig. 4. The spatial distributions of transverse focusing field (a) and longitudinal accelerating field Ex (b) at t = 1.23 ps. (c) The transverse (in the center of the self-injected electron bunch) and (d) longitudinal (on the on-axis) distributions of the accelerating field Ex at t = 0.5 ps, 2 ps, 3 ps, and 5 ps, respectively. The dashed and the dot–dashed lines show the boundaries of the hollow plasma and the self-injected electron bunch in panel (a), respectively. The focusing field at is shown by the black line in panel (a). The black rectangles denote the locations of the self-injected electron bunch in panel (d).

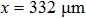
Actually, one of the remarkable advantages in the proposal is that the central intensity of the laser pulse propagates in the hollow plasma channel with the light speed for the whole laser–plasma interactions and the self-injected electrons is catching up with the laser pulse and continuously obtaining energies, until they reach the dephasing region. Figure 5 shows the space and time evolutions of the electron density and the electric field along the axis of the laser propagation, respectively. One can see that the self-injected electron bunch always stays close to the rear of the bubble in the whole laser–plasma interactions and is quasi-phase-stably accelerated forward. It demonstrates that the phase velocity of the bubble nearly equals to the velocity of the self-injected electron bunch and the dephasing length increases avoiding the slipping of the self-injected electron bunch from the accelerating phase into the decelerating phase. In Fig. 5(a), we also present the times of the first (t = 0.7 ps), second (t = 1.23 ps), and third (t = 2.12 ps) crossing of electrons on the propagating axis reflected from the channel boundary, respectively. It denotes that a self-injected electron bunch could be formed after the second crossing and its longitudinal width almost keeps a constant in the following time. On the other hand, most of self-injected electrons are confined radially in the hollow plasma channel without apparent transverse oscillations, which can be favorable to suppress the radiation loss.^[32] Consequently, a self-injected electron bunch with a narrow energy spread and small angular divergence is accelerated steadily during the whole interaction distance.

Fig. 5.

	Figure Option ViewDownloadNew Window
	Fig. 5. Space and time evolution of the electron density (a) and the electric field Ex (b) on the propagating axis of the laser pulse. The times of the first (t = 0.7 ps), second (t = 1.23 ps), and third (t = 2.12 ps) crossing of self-injected electrons on the on-axis (y = 0) are shown in panel (a).

As a comparison, simulations with the same laser pulse as that in Fig. 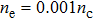1 but homogeneous densities with and are performed as shown in Fig. 6. Figure 6(a) shows that the rear part of laser pulse overtakes the front part, and is diffracted to the lateral sides of the bubble front since it is not guided in the ion channel. This leads to several electron cavities beside the bubble front. Although its energy spread is still about 8% as shown in Fig. 6(c), the self-injected electron bunch is pushed out of the bubble. As increasing the plasma density up to , it shows that the laser pulse is depleted gradually in a shorter distance compared with the case of Fig. 6(a). The self-injected electron bunch outruns the bubble wakefield and moves into the bubble front as shown in Fig. 6(b). The quality of the electron bunch will be deteriorated, which can be proved by the mulit-peak spectrum of electrons as shown in Fig. 6(d). Therefore, the nonlinear evolution of laser pulse in the homogeneous density plasma is disadvantages to obtain high-quality electron bunch.

Fig. 6.

	Figure Option ViewDownloadNew Window
	Fig. 6. (a) The electron density distribution and (c) the energy spectrum of electrons in the homogeneous plasma with density at t = 3 ps. (b) The electron density and (d) the energy spectrum of electrons in the homogeneous plasma with density at t=1.9 ps.

In order to investigate the effects of plasma densities on the quality of the self-injected electron bunch, the same laser pulse as that in Fig. 1 is irradiated into different hollow channels. Figure 7 shows that the distributions of electrons at t=2.8 ps for different densities , , , and , respectively. The dashed lines also show the boundaries of the hollow plasma channel. It shows that the quality of self-injected electron bunch is deteriorated with the increasing of the plasma density. Multiple self-injections can be observed in high density plasma, which further destroys the quality of the self-injected electron bunch. Multi-peak energy spectra of the self-injected electron bunch can be observed for the higher plasma density as shown in Fig. 8. In order to using a more realistic density profile in the hollow channel, smooth edges of the hollow channel are performed in the simulations. Figure 9 shows the distributions of electron densities and energy spectra with more smooth edge of the hollow channel. The electron density of Fig. 9(a) decreases linearly to zero from the radius to (dashed line), while it decreases linearly to zero from the radius to (dashed line) in Fig. 9(b). It shows that electrons in the channel wall can also be self-injected in the bubble and confined in the rear of the bubble. The self-injected electron bunch can be phase-stably accelerated forward and keep its monoenergetic spectrum for a long distance. It should be noted that the quality of self-injected electron bunch is better with the decreasing of electrons in the hollow channel. Therefore, our model can also be applicable to the hollow channel with a more realistic density profile.

Fig. 7.

	Figure Option ViewDownloadNew Window
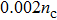
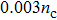
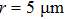
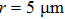
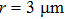
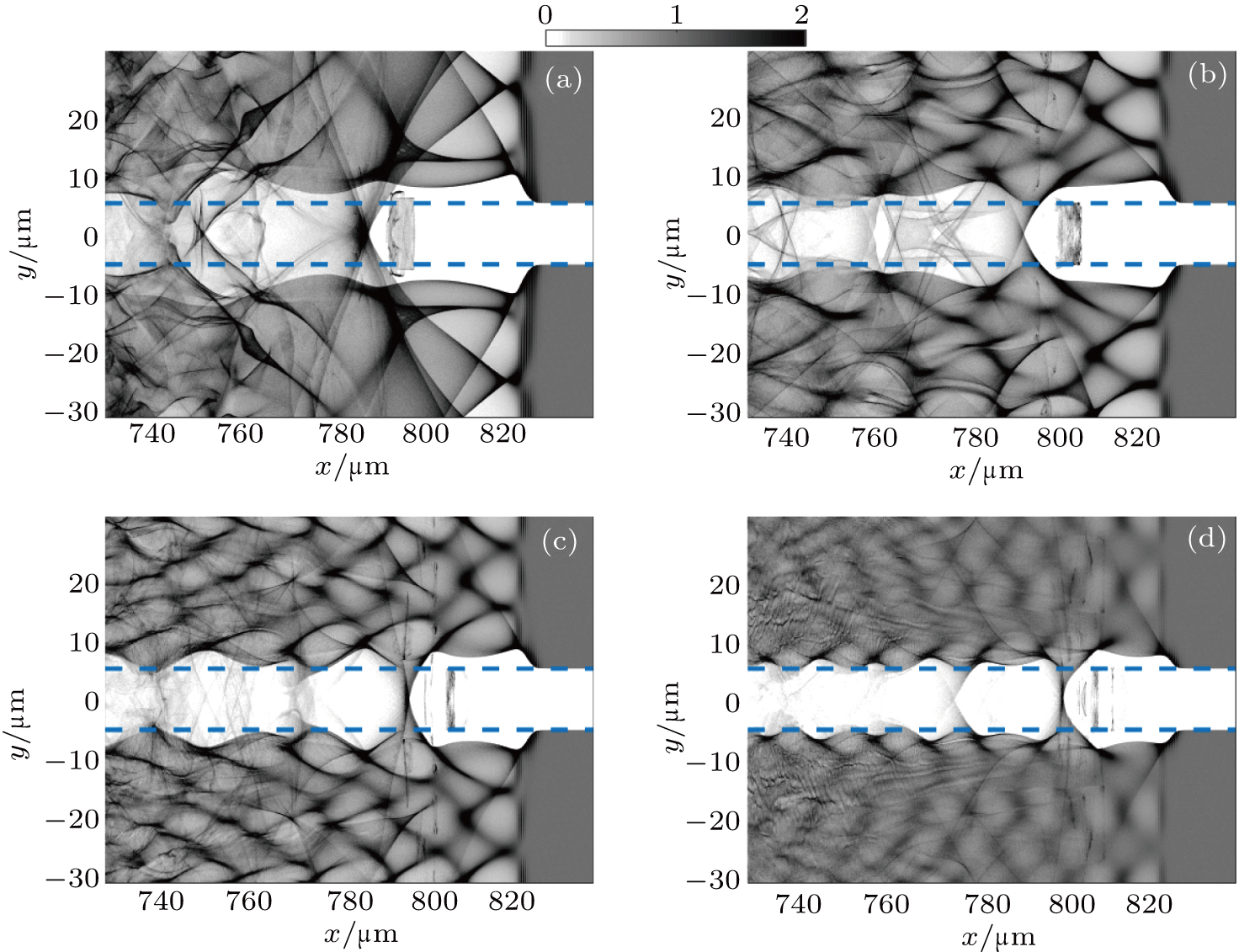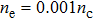
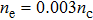
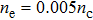
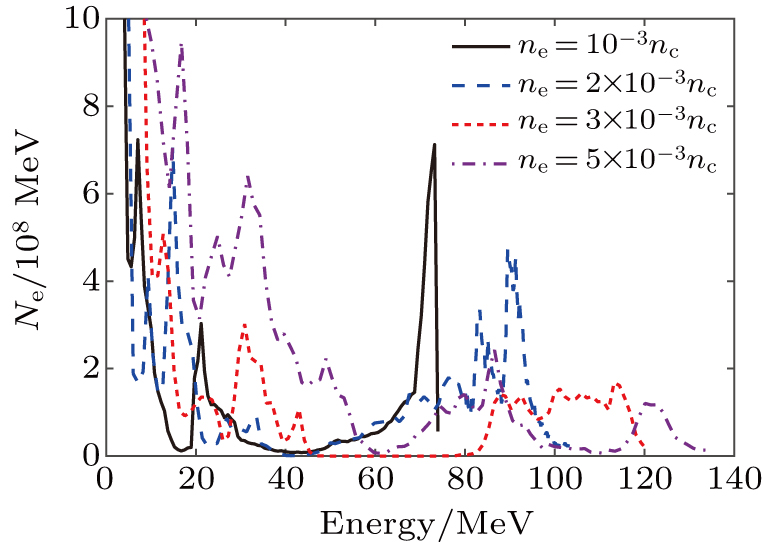	Fig. 7. The distributions of electrons at t=2.8 ps with density (a), (b), (c), and (d), respectively. The dashed lines show the boundaries of the hollow plasma channel.

Fig. 8.

	Figure Option ViewDownloadNew Window
	Fig. 8. The energy spectra of electrons at t=2.8 ps for different densities (solid line), (dashed line), (dotted line), and (dash–dotted line), respectively.

Fig. 9.

Figure Option ViewDownloadNew Window

Fig. 9. (a) The electron density distribution and (c) the energy spectrum of electrons at t = 5 ps. (b) The electron density distribution and (d) the energy spectrum of electrons at t=4.2 ps. The electron density in panel (a) decreases linearly to zero from the radius to , while the electron density in panel (b) decreases linearly to zero from the radius to . The dashed lines in panel (a) and panel (b) show the boundaries of the hollow plasma channel.

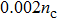
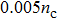
In summary, the self-injection and acceleration of electrons in the hollow plasma channel driven by the laser pulse has been investigated. The whole acceleration process of electrons could be roughly considered as the following three stages: (i) electron self-injection stage, (ii) electron oscillation stage, and (iii) electron quasi phase-stable acceleration stage. Due to no focusing field inside the channel, the self-injected electrons move radially and then they are reflected by the radial focusing force near the channel boundary. After several oscillations between the upper and lower boundaries of the hollow plasma channel, a self-injected electron bunch is formed in the rear of the bubble. And other self-injected electrons behind the bunch in the bubble will be dispersed out of the channel because there is no confining potential well around the channel edges. The self-injected electron bunch could be quasi-phase-stably accelerated forward in the whole laser–plasma interactions till the dephasing region. Meanwhile, the accelerating electric field experienced by the self-injected electron bunch is transversely uniform and nearly flatten longitudinally. Thus, a wide self-injection electron bunch can be generated and accelerated stably to the peak energy 117 MeV with the energy spread of only 2.9%.

The authors would like to thank Prof. Hong-Yu Wang for his contributions to the computational technique.