† Corresponding author. E-mail:
We review the recent progress in the study of topological phases in systems with space–time inversion symmetry IST. IST is an anti-unitary symmetry which is local in momentum space and satisfies 
The energy band structure of a periodic crystal consists of a mapping from a crystal momentum 
 |
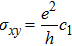
On the other hand, when the system satisfies a certain symmetry condition, the corresponding Bloch wave functions can be real-valued. Here the relevant symmetry is so-called the space–time inversion symmetry IST:(t,
 |
In fact, the gapped band structures of real Hamiltonians are topologically distinguished by different topological invariants, so-called the Stiefel–Whitney numbers.[9–11] The first and the second Stiefel–Whitney numbers w1 and w2, respectively, are the corresponding 1D and 2D topological invariants.[7,12] The Stiefel–Whitney numbers w1 and w2 are rooted in the mathematical structure of real vector bundles associated with real Bloch wave functions, which is nothing but the Stiefel–Whitney class, characterizing the twist of real Bloch states in momentum space. Although the concept of Stiefel-Whitney numbers is not popular in condensed matter physics, their physical implication is quite transparent. Namely, w1 is equivalent to the quantized Berry phase, while w2 is equivalent to the Z2 monopole charge of a nodal line, both are well-defined in systems with space–time inversion symmetry. The correspondence between the Stiefel–Whitney number and the relevant physical invariant is summarized in Table
| Table 1. The correspondence between the physics terminology and Stiefel–Whitney (Stiefel–Whitney) class in systems with space–time inversion symmetry. d indicates the spatial dimension. . |
The band crossing condition changes significantly in the presence of the reality condition given in Eq. (
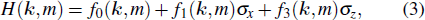 |
In fact, a line node of a 3D nodal line semimetal can also be characterized by another topological invariant, that is, the second Stiefel–Whitney number w2. Namely, a line node of a 3D nodal line semimetal carries two Z2 topological indices w1 and w2, and thus it is doubly charged.[13] As shown in Ref. [5], w2 is equivalent to the Z2 monopole charge proposed in Ref. [5]. In fact, a two-band description based on Eq. (
The significance of w2 is not limited to the characterization of monopole nodal line in 3D nodal line semimetals. When w2 is computed on the 2D Brillouin zone torus, it becomes a well-defined 2D Z2 topological invariant characterizing 2D insulators in the absence of the Berry phase.[7] Thus one can classify IST-symmetric 2D insulators into topologically trivial insulators with w2 = 0 and topologically nontrival insulators with w2 = 1, dubbed the 2D Stiefel–Whitney insulator (Stiefel–Whitney insulator).[7,14] Contrary to the 2D quantum Hall insulator that has a stable band topology and 1D chiral edge states, the 2D Stiefel–Whitney insulator is an obstructed atomic insulator, which can support zero-dimensional corner charges in the presence of additional chiral symmetry.[7,14–22] The 2D Stiefel–Whitney insulator can also be used as a basic building block for novel 3D topological insulators such as 3D weak and strong Stiefel–Whitney insulators as shown in Refs. [7] and [23]. Table
| Table 2. Correspondence between the first Chern class and the second Stiefel–Whitney class. . |
The rest of the paper is organized as follows. The mathematical definitions of the first and the second Stiefel–Whitney classes are given in Section
Here we provide the mathematical definitions of Stiefel–Whitney classes, which basically indicate the topological obstruction to defining real wave functions smoothly over a closed manifold.
The first Stiefel–Whitney class measures the orientability of real occupied wave functions over a closed 1D manifold. Namely, the real occupied wave functions are orientable (non-orientable) when w1 = 0 (w1 = 1).
In general, the orientation of a real vector space refers to the choice of an ordered basis. Any two ordered bases are related to each other by a unique nonsingular linear transformation. When the determinant of the transformation matrix is positive (negative), we say that the bases have the same (different) orientation. After choosing an ordered reference basis {v1, v2,...}, the orientation of another basis {u1,u2,...} is specified to be positive (negative) when the basis has the same (different) orientation with respect to the reference basis.
Real wave functions defined on the Brillouin zone can be considered as real unit basis vectors defined at each momentum, that is, they form a structure of a real vector bundle over the Brillouin zone. The basis can be smoothly defined locally on the manifold, but may not be smooth over a closed submanifold 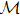

Interestingly, the orientablity of real wave functions can be determined by the Berry phase computed in a smooth complex gauge, such that w1 = 1 (w1 = 0) indicates that the relevant wave functions carry π (0) Berry phase. Namely, the first Stiefel–Whitney number defined in a real basis is equivalent to the well-known quantized Berry phase defined in a smooth complex basis. This correspondence can be seen by investigating how the π Berry phase computed with the smooth complex state |un
 |
 |


 |
 |


 |
In fact, the first Stiefel–Whitney number w1 determines the orientability of real states even in higher dimensions.[10] From the analysis in 1D, we find
 |


The second Stiefel–Whitney class describes whether a spin (or pin) structure is allowed or not for given real wave functions defined on a 2D closed manifold 
Let us consider real occupied states |{um





 |

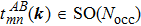
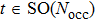


In general, the transition functions should satisfy the following consistency conditions:[9]
 |
 |
However, when we consider the lifting of transition functions to the double covering group at all overlapping regions in 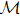

 |
 |




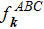
Let us now examine the case in which a lift that satisfies the consistency conditions can be found. In general, there is no obstruction for the first consistency condition in Eq. (
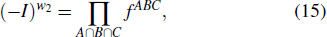 |

For instance, let us illustrate how w2 is defined on a spherical manifold, which is directly relevant to the Z2 monopole charge of a nodal line. First we consider three patches A, B, and C covering a sphere shown in Fig.
 |
 | Fig. 1. Three patches covering a sphere. (a) Orthographic view. ϕ and θ are the azimuthal and polar angles. B and A (C) overlap at ϕ = 0 (ϕ = π), and A and C overlap at ϕ = π/2. The north pole at θ = 0 and the south pole at θ = π are triple overlaps. (b) Top view. Overlapping regions are exaggerated for clarity. Figures are adopted from the supplemental materials in Ref. [7]. |
Now let us define
 |


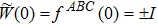




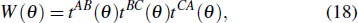 |
Here we describe the topological phases in IST-symmetric systems characterized by the first Stiefel–Whitney number w1. In 1D, w1 computed over the full Brillouin zone is the bulk topological invariant of insulators with quantized charge polarization. In 2D (3D), w1 is defined on a closed loop enclosing a point (line) node, and plays the role of a topological charge carried by the node. In all these cases, the low-energy properties of the system can be generally described by the 2 × 2 effective Hamiltonian in Eq. (
 |
In 1D, since there is only one momentum variable k for a given tuning parameter m, the gap-closing condition in Eq. (
| Table 3. Comparison of the topological phases characterized by the first Stiefel–Whitney number w1 and the second Stiefel–Whitney number w2. Here TI (SWI) indicates a topological insulator (Stiefel–Whitney insulator). DSM (NLSM) denotes a Dirac semimetal (nodal line semimetal). A monopole nodal line indicates a nodal line with Z2 monopole charge. . |
To describe the relation between the topological property of an insulator and w1, let us consider 1D insulators described by the Su–Schuriffer–Heeger (SSH) model.[25] Although the properties of the corresponding topological insulator are already well-known, here we describe the SSH model by using a real basis and illustrate the relevant topological property in the context of the first Stiefel–Whitney number. The SSH Hamiltonian is given by
 |
 |
First, let us impose the reality condition on |uv⟩ over the whole 1D Brillouin zone by choosing the gauge ei ϕv(k) = 1. Figures
 | Fig. 2. The amplitudes of the occupied state of the SSH model. Red and orange lines show the first and second components of the occupied state in Eq. ( |
On the other hand, if the reality condition is relaxed by choosing ϕv(k) = k/2, the occupied state becomes globally smooth in both |t| < 1 and |t| > 1 cases [see Figs. 
In 2D, the gap-closing condition in Eq. (
The stability of the Dirac points in the resulting Dirac semimetal phase can be understood in the following way. Since the Berry curvature Fxy(
After the discovery of graphene, it has been well-known that a stable 2D Dirac point can exist in PT-symmetric 2D spinless fermion systems. However, in this system, it is also known that the Dirac point becomes unstable once the spin–orbit coupling is turned on. Therefore finding a Dirac point stable in the presence of spin–orbit coupling is an interesting open question. One interesting idea proposed in Refs. [29] and [30] is to use the nonsymmophic crystalline symmetry which protects four-fold degenerate Dirac points at the corners of the Brillouin zone in 2D centrosymmetric systems.
On the other hand, in the case of 2D noncentrosymmetric systems, C2zT symmetry can protect Dirac points with two-fold degeneracy whose location can be anywhere in the Brillouin zone.[5] One can call a gap-closing point with two-fold degeneracy as a 2D Weyl point, which is distinguished from four-fold degenerate Dirac points in centrosymmetric systems. As long as the inversion is broken, and thus the spin splitting occurs at a generic momentum, the above description in Eq. (
 |
 | Fig. 3. (a) Evolution of the band structure of a 2D noncentrosymmetric system with IST symmetry as a tuning parameter m increases. (b) Trajectories of 2D Weyl points in the intermediate semimetal phase as m increases. ⊙ and ⊗ are the locations where pair creation and pair annihilation happen. Figures are adopted from the supplemental materials in Ref. [6]. |
In 3D, the gap-closing condition in Eq. (
Here we describe the properties of topological NLSM in 3D whose nontrivial topology is characterized by the second Stiefel–Whitney class. We first show that the Z2 monopole charge of a NL defined on the wrapping sphere is equivalent to the second Stiefel–Whitney number w2. Based on this equivalence, we apply the mathematical property of the second Stiefel–Whitney class to the problem of 3D nodal line semimetals, and predict the fundamental topological properties of the nodal line semimetals with Z2 monopole charges.
In 3D PT-symmetric spinless fermion systems, an accidental band crossing described by the 2 × 2 effective Hamiltonian in Eq. (
However, recently it has been proposed that there is another type of nodal lines carrying Z2 monopole charge (monopole nodal line).[42] A single monopole nodal line cannot be gapped and thus stable. To annihilate a monopole nodal line, one needs to introduce another monopole nodal line, and then the nodal line pair can be pair annihilated. To describe a monopole nodal line, one needs to go beyond the two-band description given in Eq. (
 |


Moreover, there is another intriguing nodal structure in the bands that the Hamiltonian in Eq. (
Now let us illustrate the mechanism for the pair creation of monopole nodal lines, which is a sequence of band inversions described in Fig.
 | Fig. 5. Pair creation of nodal lines carrying Z2 monopole charge (monopole nodal lines) via a double band inversion (DBI). (a) Evolution of band structure during DBI. Red (orange) points and lines indicate the crossing between the conduction and valence bands (two occupied bands). (b) Saddle-shaped band structure when 0 < M < |m|. (c) Change in nodal line structure when two saddle-shaped bands cross. Figures are adopted from the supplemental materials in Ref. [7]. |
 | Fig. 6. A torus T2 wrapping the nodal line γ1 in the Brillouin zone. T2 is thin enough so that it does not intersect any other band degeneracies. Red lines (γ1 and γ6) are lines of touching between the conduction and valence bands. Orange (γ3 and γ4) and green (γ2 and γ5) lines are lines of touching between the first and the second topmost occupied bands and between the second and the third topmost occupied bands, respectively. Only the linking between γ1 and γ3 is protected as it generates the nontrivial second Stiefel–Whitney number on T2, whereas the linking between γ1 and γ5 is not protected [See Eq. ( |
Now let us discuss the equivalence between the second Stiefel–Whitney number w2 and the Z2 monopole charge of a nodal line. The equivalence follows from the fact that the nontrivial Z2 monopole charge forbids the existence of the spin structure on a sphere enclosing the nodal line. Let us first briefly review the idea of the Z2 monopole charge that is defined over a sphere enclosing a nodal line.[42] For this, we divide the wrapping sphere into two patches, each covering the northern (N) or the southern (S) hemisphere, which overlap along the equator. 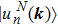

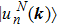

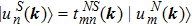
Interestingly, this Z2 monopole charge also characterizes the obstruction to having a spin structure over the wrapping sphere. For simplicity, let us take a gauge where the transition function tNS(

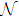
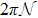
Since the equivalence between the Z2 monopole charge and the second Stiefel–Whitney number w2 has been established, one can use the mathematical properties of Stiefel–Whitney numbers to understand the physical properties of monopole nodal lines. One important mathematical property of Stiefel–Whitney numbers is the so-called Whitney sum formula, which provides the rule for determining the total second Stiefel–Whitney number of blocks of bands from w1 and w2 of each block. Using the Whitney sum formula, one can show that w2 of nondegenerate occupied bands can be expressed by the Berry connection as
 |
To explain the Whitney sum formula, let us suppose that the set of the occupied bands 
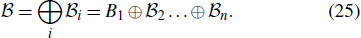 |
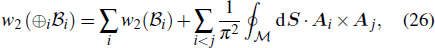 |

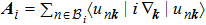
 |

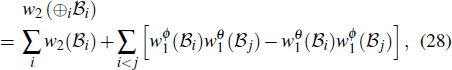 |

One important physical implication of the Whitney sum formula given in Eq. (
To show the relation between w2 and the linking number, let us consider a sphere enclosing a nodal line γ1 at the Fermi level. w2 defined on the sphere is identical to the Z2 monopole charge of the nodal line γ1. Now we smoothly deform the sphere into a torus while keeping the energy gap finite during the deformation. Then, w2 computed on the sphere and the torus should be the same. If the torus T2 wrapping γ1 is thin enough, all the occupied bands can become non-degenerate everywhere on the torus. Then, because the w2 of a non-degenerate band is zero, the Whitney sum formula becomes 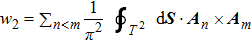
By noting that the quantization condition of the Berry phase, ∮C An = π or 0, resembles the Ampere’s law in electromagnetics, one can solve the equation and get a solution analogous to the Bio–Savart law. Explicitly, let us start from the differential form representing the quantization of the Berry phase, which is similar to the differential form of the Ampere’s law,
 |
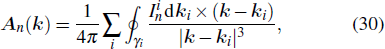 |
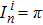

By using this formula of the Berry connection, we have
 |
 |
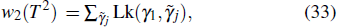 |




Let us explain how the second Stiefel–Whitney number w2 can be computed by using the Wilson loop method. The Wilson loop operator is defined by[48–50]
 |
First, let us consider a sphere in the Brillouin zone, which is covered by three patches A, B, and C whose overlaps A ∩ C, C ∩ B, and B ∩ A are at ϕ = π/2, ϕ = π, and ϕ = 2π, respectively, for all 0 ≤ θ ≤ π [see Fig.
 |


 |
 |
 | Fig. 7. Patches covering a sphere and a torus. Wilson loop operators are calculated along the red arrows. (a) Sphere covered with three patches which overlap on ϕ = 0, ϕ = π/2, and ϕ = π. (b) Torus covered with four patches. ϕ and θ are 2π-periodic. Transition functions are taken to be nontrivial only over θ = 0 and ϕ = 0 lines. Figures are adopted from the supplemental materials in Ref. [7]. |
Figures
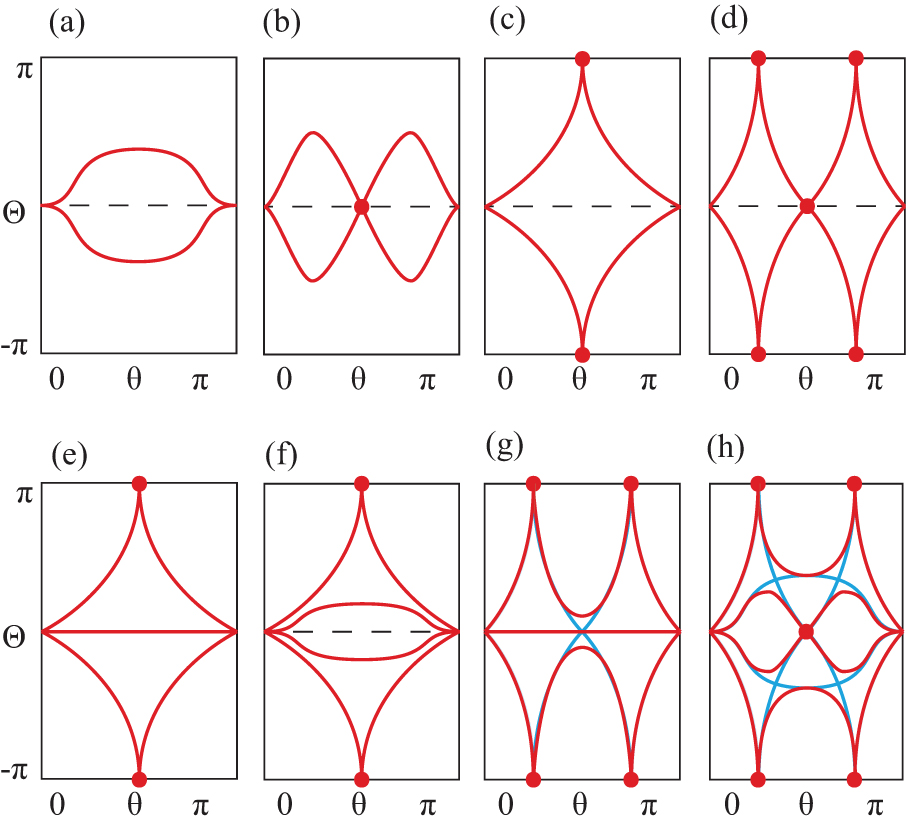 | Fig. 8. Wilson loop spectra on a sphere. The Wilson loop operator is calculated along the azimuthal direction with a fixed polar angle θ. (a)–(d) When the number of occupied bands Nocc is two. The winding number is (a), (b) zero, (c) one, and (d) two. (b) can be adiabatically deformed to (a) as we push the crossing point on Θ = 0 out of the boundary at θ = 0 or θ = π. (e)–(h) When Nocc = 3 or Nocc = 4. (e) has a flat spectrum on Θ = 0 in addition to (c). Adding a small perturbation to (e) does not deform the spectrum when Nocc = 3, while it deforms the spectrum to (f) when Nocc = 4. Panels (g) and (h) show the Z2 nature of the Wilson loop spectrum for Nocc = 3 and Nocc = 4, respectively. Blue lines in (g) and (h) are obtained after adding one and two flat bands to (d), respectively, whereas red lines are the spectrum after adding a PT-preserving deformation which eliminates non-protected crossing points. The crossing points on Θ = π can always be pair-annihilated after this deformation. Figures are adopted from the supplemental materials in Ref. [7]. |
Let us note that the parity of the winding number, which is equivalent to the second Stiefel–Whitney number, is given by the parity of the number of crossing points on Θ = π. Thus, we can get w2 by counting the number of the crossing points on the line. This is also true when the number of occupied bands is larger than two because the crossing points on Θ = π are stable even when additional trivial bands are added.
While a single linear crossing point is locally stable on the line Θ = nπ for any integer n, two linear crossing points on the same line may be pair-annihilated. In fact, one important difference between Nocc = 2 and Nocc > 2 cases is that a pair annihilation, which is forbidden in the former case, is always possible in the latter case. In the case of two occupied bands, two linear crossing points on the line Θ = π at θ = θ1 and θ = θ2 cannot be pair-annihilated if there is a linear crossing point on the Θ = 0 line at θ = θ0 satisfying θ1 < θ0 < θ2 [see Fig.
For later use, let us briefly explain how the Wilson loop operator can be computed on a torus and it is related with the second Stiefel–Whitney number. Similar to the case on a sphere, the homotopy class of the Wilson loop operator W0(θ) determines the second Stiefel–Whitney number w2 gauge-invariantly from the spectrum of W0(θ). Namely, w2 can be determined by counting the number of the crossing points on Θ = π. The Wilson loop operator on a torus can be related to the transition function as follows. Let us consider a torus covered with four patches shown in Fig.
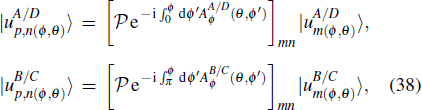 |
 |
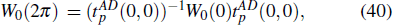 |



In Ref. [7], based on first-principles calculations, ABC-stacked graphdiyne is proposed to realize monopole nodal lines with the linking structure. ABC-stacked graphdiyne refers to an ABC stacking of 2D graphdiyne layers composed of sp2–sp carbon network of benzene rings connected by ethynyl chains [see Fig.
 | Fig. 9. (a) Band structure near a nodal line with zero Z2 monopole charge. (b) Band structure near a nodal line carrying a unit Z2 monopole charge (monopole nodal line) linked with another nodal line below the Fermi level (EF). (c) Atomic structure of ABC-stacked graphdiyne. (d) Band structure of ABC-stacked graphdiyne, where thick orange lines indicate degenerate nodal lines above and below EF. (e) The shape of two monopole nodal lines (red loops) at EF (E = 0) linked with a nodal line below EF (yellow line) in ABC-stacked graphdiyne. Figures are adopted from Ref. [7]. |
Let us briefly mention the influence of time-reversal symmetry breaking and spin–orbit coupling. When time-reversal symmetry is broken due to effective Zeeman effect, a monopole nodal line semimetal turns into an axion insulator with quantized magnetoelectric polarizability as shown in Ref. [7]. On the other hand, when spin–orbit coupling is not negligible, a monopole nodal line semimetal becomes a higher-order topological insulator with helical hinge states.[18] These examples clearly show that monopole nodal line semimetal materials can be considered as a parent state leading to various novel topological insulators under suitable conditions.
Up to now, we have considered w2 defined on a sphere or a torus enclosing a nodal line, which is embedded in 3D momentum space. In this section, we consider w2 as a topological invariant that classifies 2D IST-symmetric insulators, in which w2 is defined on the entire 2D Brillouin zone torus.
2D IST-symmetric insulators can be characterized by the Wilson loop spectrum on the 2D Brillouin zone. The 2D Brillouin zone can be viewed as a 2D torus, parametrized by two periodic cycles (ϕ,θ) = (kx, ky) along which occupied states may be non-orientable, contrary to the case on a sphere where occupied states are always orientable. If the Wilson loop operator is calculated along a non-orientable cycle, its spectrum cannot reveal the topological property due to the possible flat spectra existing on the Θ = 0 and Θ = π lines. For this reason, we only consider the Wilson loop operators calculated along the orientable cycles below. More subtle issues related with the non-orientability were discussed in detail in Ref. [7].
Figure
 | Fig. 10. Wilson loop spectra on a torus. The Wilson loop operator is calculated along the orientable ϕ cycle at a fixed θ. (a)–(d) Spectrum when Nocc = 2 for (w1,θ,w2) of (a) (0,0), (b) (1,0), (c) (0,1), (d) (1,1). (e) Nontrivial spectrum when Nocc = 3 with w2 = 1. When the number of occupied bands is odd, w2 can be determined only if we calculate the Wilson loop operator along a orientable cycle. (f)–(h) Nontrivial spectrum when Nocc = 4 for (w1,θ,w2) of (f) (1,0), (g) (0,1), (h) (1,1). Here, w1,θ is the first Stiefel–Whitney number computed along the θ direction. Figures are adopted from the supplemental materials in Ref. [7]. |
What makes the Wilson loop spectrum on a torus distinct from that on a sphere is the boundary condition of the Wilson loop operator. While W = 1 at θ = 0 and π on a sphere, the periodic boundary condition in Eq. (
When Nocc is even, there are four distinct types of Wilson loop spectra. For instance, figures
 |
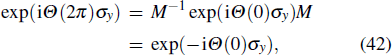 |
It is worth noting that w2 and the corresponding Wilson loop spectrum may change depending on the unit cell choice when w1,θ = 1. Notice that the spectra in Figs.
Although the general integral form of w2 is not known, an integral form of w2 can be found in some special cases. In particular, when Nocc = 2 and the occupied bands are orientable, w2 is identical to the parity of the Euler invariant e2. The Euler invariant e2 is an integer topological invariant for two real bands which can be written as a simple flux integral form[9,10,44]
 |



The flux integral form of e2 can be connected to transition functions in the following way. To show this relation, let us notice that the 2D Brillouin zone can be deformed to a sphere when the real states are orientable along any non-contractible one-dimensional cycles as far as the topology of the real states is concerned. Then the sphere can be divided into two hemispheres, the northern (N) and southern (S) hemispheres, which overlap along the equator. Along the equator, the real smooth wave functions 

 |
One physical consequence resulting from a nonzero Euler invariant e2 is the existence of anomalous corner charges. The presence of corner charges can be understood in terms of the effective Hamiltonian for boundary states.[18] Here let us briefly explain the idea. Suppose that a two-dimensional system is composed of two quantum Hall insulators with Chern numbers c1 = 1 and c1 = −1, respectively, which are related to each other by IST. This system is an Euler insulator with e2 = 1, which can be confirmed by the winding pattern of the Wilson loop spectrum. In this particular limit of the Euler insulator, two counter-propagating chiral edge states exist. The edge states are fully gapped after two IST-symmetric mass terms m1 and m2 are added. Each of the two mass terms has 4Ni = 1,2 + 2 zeros due to the IST symmetry condition m1,2(θ) = −m1,2 (−θ), where θ denotes the angular coordinate of the circular boundary of a disk-shaped finite-size system, and Ni = 1,2 are non-negative integers. The band gap of the edge spectrum 
The band topology associated with the nonzero Euler class is fragile. Namely, the Wannier obstruction of an Euler insulator with e2 ≠ 0 disappears after additional trivial bands are introduced below the Fermi level.[14] Although the Euler class is defined only for two band systems, its parity still remains meaningful even after additional trivial bands are introduced. Namely, if the Euler class of the two-band model is even (odd), w2 of the system should remain zero (one) after the inclusion of additional trivial bands.[7] Such a change of the topological indices from Z to Z2 can also be observed from the variation of the winding pattern in the Wilson loop spectrum when additional trivial bands are added.[7,17] In fact, such fragility of the winding pattern in the Wilson loop spectrum reflects the fragility of the Wannier obstruction.[7,16–18] Although the nontrivial second Stiefel–Whitney number (w2 = 1) does not induce a Wannier obstruction when the number of bands is bigger than two, anomalous corner states can still exist. Here the corner charges are induced by the configuration of the Wannier centers constrained by the non-trivial second Stiefel–Whitney number.[14]
Since the second Stiefel–Whitney number determines not only the Z2 monopole charge of a nodal line on its wrapping sphere but also the Z2 topological invariant of a 2D Stiefel–Whitney insulator, an intriguing topological phase transition mediated by monopole nodal lines can occur in 3D PT-symmetric systems. To describe this, let us start with a sphere wrapping a monopole nodal line in momentum space, and deform it into two parallel 2D planes with fixed kz. Then each 2D plane can be considered as a 2D subsystem with PT symmetry. Since the monopole charge of the nodal line is identical to the difference of w2 of these two planes, if w2 = 0 in one plane, w2 = 1 in the other plane. Armed with this information, let us start from a 3D normal insulator and assume that a pair of monopole nodal lines is created at the Γ point by tuning a parameter M. Then every 2D subspace with fixed kz has w2 = 1 when its kz lies between the monopole nodal line pair whereas the other 2D subspaces with kz on the other side of the Brillouin zone should have w2 = 0. After the two monopole nodal lines are pair annihilated at the Brillouin zone boundary, one can expect that every 2D slice of the Brillouin zone with fixed kz has w2 = 1, which is the definition of a 3D weak Stiefel–Whitney insulator. This phase can be considered as a vertical stack of weakly interacting 2D Stiefel–Whitney insulators. In general, a 3D weak Stiefel–Whitney insulator is characterized by three Stiefel–Whitney numbers defined on kx = π, ky = π, and kz = π planes, respectively. The three invariants encode the three stacking directions of 2D subsystems. The invariants can be changed only when monopole nodal line pairs are created and then annihilated at the Brillouin zone boundary after traversing the full Brillouin zone, which is analogous to the topological phase transition between a 3D Chern insulator and a normal insulator mediated by Weyl points.[53]
To demonstrate the topological phase transition, let us consider a lattice regularization of Eq. (
 |
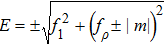

Since we have a new 2D Z2 invariant w2 and the associated 2D Z2 topological insulator (2D Stiefel–Whitney insulator), it is natural to ask whether one can find a 3D topological insulator associated with the second Stiefel–Whitney class. In spinless fermionic systems with IST = PT, real wave functions can be defined over the full 3D Brillouin zone. However, unfortunately, there is no corresponding 3D topological invariant.[13,54] So we do not expect a 3D topological insulator associated with the Stiefel–Whitney number other than the 3D weak Stiefel–Whitney insulator discussed above. Instead, we focus on the 3D systems with IST = C2zT where the z-axis is chosen as the axis for C2 rotation. In C2zT-symmetric 3D systems, only the wave functions on the kz = 0 and kz = π planes can be real with the corresponding second Stiefel–Whitney numbers w2(0) and w2(π), respectively. Thus, a 3D strong Z2 topological invariant Δ3D may be defined as Δ3D ≡ w2(π) − w2(0) in a way similar to how the 3D Fu–Kane–Mele invariant is constructed. Since Δ3D originates from w2 in IST-invariant planes, the 3D topological insulator with Δ3D = 1 can be called a 3D strong Stiefel–Whitney insulator. Let us note that the idea of C2zT-protected Z2 topological insulator was already proposed in Ref. [5]. However, its bulk electromagnetic response and the related hinge excitations were studied recently in Refs. [23] and [55]. In fact, a strong 3D Stiefel–Whitney insulator is an example of higher-order topological insulators whose bulk magnetoelectric response is described by the axion term with the quantized magnetoelectric polarizability P3 = 1/2. As a result of the bulk boundary correspondence associated with the quantized P3, we show that a 3D strong Stiefel–Whitney insulator has chiral hinge states[56–65] along the edges parallel to the rotation axis and 2D massless Dirac fermions on the surfaces normal to the rotation axis as shown in Fig.
 | Fig. 12. 3D strong Stiefel–Whitney insulator protected by C2zT symmetry. (a) Schematic figure describing the second Stiefel–Whitney number on the C2zT-invariant planes in momentum space. In a 3D strong Stiefel–Whitney insulator, w2(kz = π) − w(kz = 0) = 1 modulo two. (b) Schematic figure describing the gapless states on the surface and hinges in real space. An odd number of 2D Dirac fermions appear on each of the top and bottom surfaces. 1D chiral fermions appear on the side hinges. Figures are adopted from Ref. [23]. |
The equivalence between Δ3D and the quantized magnetoelectric polarizability can be shown by analyzing the homotopy group of the sewing matrix G for IST symmetry defined as
 |
 |
 |
In a smooth complex gauge, the magnetoelectric polarizability P3 takes the form of the 3D Chern–Simons invariant[66,67]
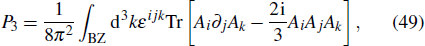 |
 |
 |
The relation between the bulk topological invariant of the axion insulator and that of the 2D Stiefel–Whitney insulator implies a similar relation between their anomalous boundary states. In fact, the chiral hinge states in an axion insulator can be considered to result from the pumping of charges at the corners of the Stiefel–Whitney insulator when kz is regarded as a parameter for the pumping process.[55] This charge pumping picture can be extended further to the cases with strong spin–orbit coupling. Here one can consider a helical charge pumping, where the corner charges with different spins are pumped to the opposite directions, which leads to a construction of a higher-order topological insulator with helical hinge states.[14,45,57]
The Stiefel–Whitney classes are examples of characteristic classes, which are the cohomology classes associated to vector bundles, describing how the corresponding vector bundle is twisted.[10,11] There are mainly four different types of characteristic classes known up to now: Chern classes, Stiefel–Whitney classes, Euler Classes, and Pontryagin classes.[10,11] While the idea of Chern classes and associated topological invariants, such as Chern numbers, mirror or spin Chern numbers, Fu–Kane invariants, have been widely applied to condensed matter physics, the implication of the other characteristic classes in the context of condensed matter physics is not well established yet. In this paper, we have reviewed the recent progress in the study of topological physics associated with Stiefel–Whitney numbers. More explicitly, we showed that the first Stiefel–Whitney number is equivalent to the quantized Berry phase so that the nontrivial first Stiefel–Whitney number w1 indicates either a 1D insulator with quantized charge polarization or a stable Dirac point (nodal line) in 2D Dirac semimetals (3D nodal line semimetals) in systems with space–time inversion symmetry IST. Moreover, we proved that the second Stiefel–Whitney number not only characterizes the monopole charge of nodal lines in IST-symmetric systems but also serves as a well-defined 2D topological invariant characterizing a 2D Stiefel–Whitney insulator. This idea is further extended to 3D systems with IST = PT and IST = C2zT leading to the 3D weak and strong Stiefel–Whitney insulators, respectively. Recently, monolayer graphdiyne was theoretically proposed as a 2D Stiefel–Whitney insulator. However, materials that realize the 3D strong Stiefel–Whitney insulator composed of spinless fermions are still lacking.
Also, as briefly explained, IST-symmetric two-band systems in 2D can be characterized by another characteristic class, so-called the Euler class. The Euler class is an integer topological invariant classifying real orientable two-band systems. As discussed before, a two-band system with a nonzero Euler invariant e2 has fragile band topology and supports corner charges. In fact, an Euler insulator with e2 ≠ 0 has various intriguing topological properties, which are not discussed in this review article. For instance, a two-band system with the Euler invariant e2 always possesses band crossing points whose total winding number is equal to 2e2.[14] Thus the conventional Nielsen–Ninomiya theorem fails in systems with a nonzero Euler invariant. Moreover, if an additional trivial band is coupled to the original two-band system and band crossing happens between them, the newly generated Dirac points play the role of the source of π Berry phase with a Dirac string in between, which strongly affects the braiding properties of the original Dirac points. Such a nontrivial braiding is a manifestation of the non-abelian topological charge of real wave functions, which is discussed thoroughly in Refs. [14] and [68]. To unveil novel topological physics associated with other characteristic classes is definitely one important issue for future research.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] | |
| [39] | |
| [40] | |
| [41] | |
| [42] | |
| [43] | |
| [44] | |
| [45] | |
| [46] | |
| [47] | |
| [48] | |
| [49] | |
| [50] | |
| [51] | |
| [52] | |
| [53] | |
| [54] | |
| [55] | |
| [56] | |
| [57] | |
| [58] | |
| [59] | |
| [60] | |
| [61] | |
| [62] | |
| [63] | |
| [64] | |
| [65] | |
| [66] | |
| [67] | |
| [68] |



