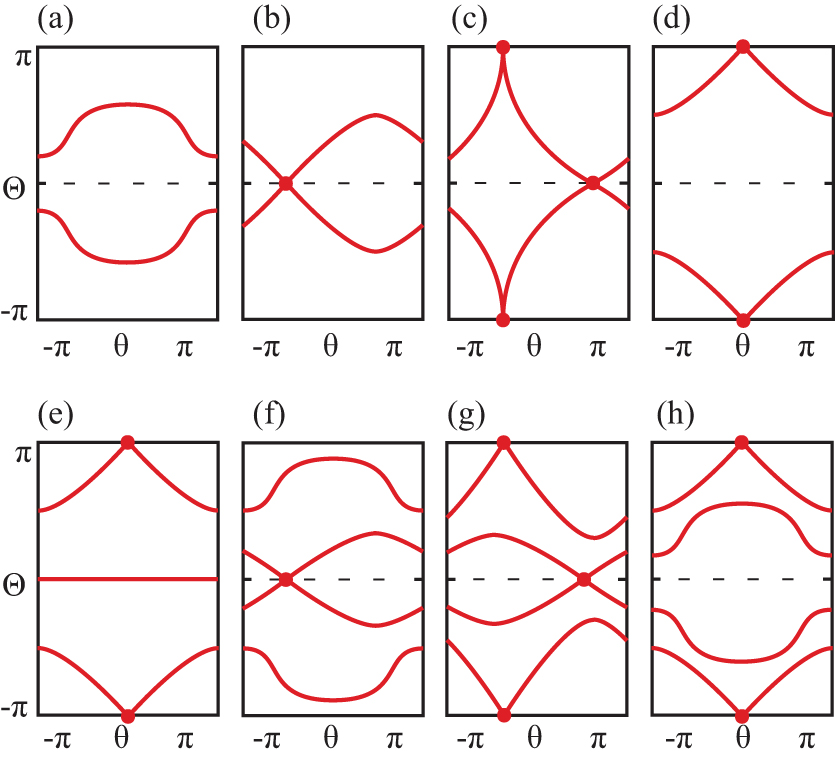
Wilson loop spectra on a torus. The Wilson loop operator is calculated along the orientable ϕ cycle at a fixed θ. (a)–(d) Spectrum when N_occ = 2 for (w_1,θ,w₂) of (a) (0,0), (b) (1,0), (c) (0,1), (d) (1,1). (e) Nontrivial spectrum when N_occ = 3 with w₂ = 1. When the number of occupied bands is odd, w₂ can be determined only if we calculate the Wilson loop operator along a orientable cycle. (f)–(h) Nontrivial spectrum when N_occ = 4 for (w_1,θ,w₂) of (f) (1,0), (g) (0,1), (h) (1,1). Here, w_1,θ is the first Stiefel–Whitney number computed along the θ direction. Figures are adopted from the supplemental materials in Ref. [7].