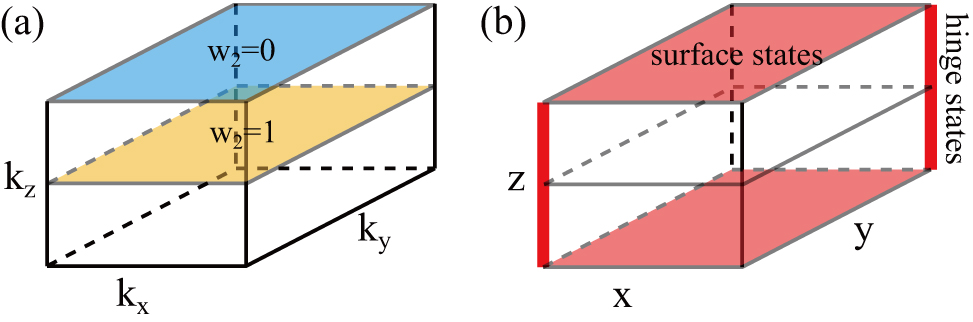
3D strong Stiefel–Whitney insulator protected by C_2zT symmetry. (a) Schematic figure describing the second Stiefel–Whitney number on the C_2zT-invariant planes in momentum space. In a 3D strong Stiefel–Whitney insulator, w₂(k_z = π) − w(k_z = 0) = 1 modulo two. (b) Schematic figure describing the gapless states on the surface and hinges in real space. An odd number of 2D Dirac fermions appear on each of the top and bottom surfaces. 1D chiral fermions appear on the side hinges. Figures are adopted from Ref. [23].