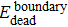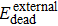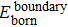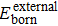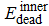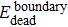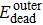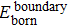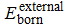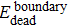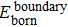† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant No. 61671142).
Studying the topology of infrastructure communication networks (e.g., the Internet) has become a means to understand and develop complex systems. Therefore, investigating the evolution of Internet network topology might elucidate disciplines governing the dynamic process of complex systems. It may also contribute to a more intelligent communication network framework based on its autonomous behavior. In this paper, the Internet Autonomous Systems (ASes) topology from 1998 to 2013 was studied by deconstructing and analysing topological entities on three different scales (i.e., nodes, edges and 3 network components: single-edge component M1, binary component M2 and triangle component M3). The results indicate that: a) 95% of the Internet edges are internal edges (as opposed to external and boundary edges); b) the Internet network consists mainly of internal components, particularly M2 internal components; c) in most cases, a node initially connects with multiple nodes to form an M2 component to take part in the network; d) the Internet network evolves to lower entropy. Furthermore, we find that, as a complex system, the evolution of the Internet exhibits a behavioral series, which is similar to the biological phenomena concerned with the study on metabolism and replication. To the best of our knowledge, this is the first study of the evolution of the Internet network through analysis of dynamic features of its nodes, edges and components, and therefore our study represents an innovative approach to the subject.
As a complex dynamic system, the Internet evolves with uncertainties over time. It is undergoing many structural changes, including the addition of new facilities and the removal of old or faulty ones. Using complex network theory, several aspects of the dynamic properties of the Internet have been studied, from the inter-dependent relationship of network devices to the economic ecosystem of the Internet.[1,2] When referring to the Internet, which is a typical example of a complex system, the behaviors among the whole system should ideally be described in a well-defined, broad approach. A classic case of using a simple formula to describe complicated processes is the logistic equation that is used to describe population dynamics, which possesses a rich structure that includes chaotic orbits and fractal non-divergent domains. Simple systems are more likely to generate more complicated behavior, in particular interacting particle systems.
Expansion and improvement of the Internet has not stopped since the day it was invented, and so it is fair to assume that changes of nodes and edges drive the network’s evolution. All of the activities related to change and evolution are simply to satisfy our needs, from commercial needs to entertainment. In recent decades, complex network theory has become an important approach to investigate most types of complex systems.[3,4] There has been a major research effort made to depict the interaction or inter-dependency among network entities of the network topologies (e.g., node, component). For example, Shen-Orr et al.[5] introduced the motif structure (a network component) into complex network studies and found an easily interpretable view of the entire known transcriptional network of the organism. Faloutsos et al.[1] worked on the power-law of degree distribution of the Internet topology and corrected the prevailing view of the Internet, according to which the Internet was seen as a random network. The Internet has become an enormous complex system[6] whose topology, function, dynamics and so on are too complicated to be described. A few studies have approached the evolution of the Internet from a different perspective. The statements regarding the changes that the Internet underwent vary from referring to the size of the Internet, the phase of the Internet, to the Internet ASes relationships. In a study of the evolution of the Internet economic ecosystem,[7] the characteristics and interactions of the application and network providers have been investigated, which show how it led to a market equilibrium of the ecosystem. However, what drives this equilibrium state of the Internet remains unclear. Some studies have observed and distinguished the birth and death of the nodes and edges.[8,9] The question remains how the network edges drive the Internet’s evolution.
The basic mechanisms of biological evolutionary phenomena are applied directly or indirectly to come up with novel designs or solve problems that are difficult to solve otherwise in network science and engineering fields.[10] Imagine a scenario in which some living organisms leave their original group and choose to join other group gradually, while some small groups tend to be involved in the bigger ones, to share certain types of resources (e.g., information, gene diversity, habitats, energy, and so on), in which each individual is trying to maximize their benefits and become robust. These series of behaviors ensure that individuals survive continuously despite limited space or resources. In contrast, those individuals who have not sought for better opportunities or supplies are more likely to die off over time. Thus, when it comes to the Internet system, the question as to how individuals, or some small groups, participate in the Internet’s evolution has become a popular topic. We regard the Internet as an instance of a complex system that exhibits simple behavior due to a compendium of innate architectural features that span a range of scientific disciplines. From this perspective, network scientists believe that large-scale studies of the Internet are valuable.[11] To study these phenomena and reveal the behaviors of individuals (i.e., nodes, edges) and groups (e.g., components) of the Internet, the analysis based on a novel perspective is applied in this paper. We analyzed the evolution dynamic of the Internet by focusing on both the birth and the death of nodes, edges and some certain network components of the Internet. Some large scale-properties from the resulting network are observed. The contributions of this work are addressed as follows:
(i) We propose a novel method to observe and analyse the Internet’s evolution, which considers nodes, edges and three specific functional network components of the Internet.
(ii) By adopting the proposed method on Internet AS-level topology data from January 1998 to August 2013, we observe a type of link adjustment, including inter-edges growth and inter-components reconstruction, which is the key factor of the AS-level Internet evolution.
(iii) Fundamental biological phenomena, such as metabolism and replication, are observed in our study when the analysis method is applied to deconstruct and construct the Internet’s network topologies.
The rest of this paper is organized as follows. Section
Because the Internet is continuously evolving in a dynamic way due to human activities, understanding how the Internet (both IP-level and AS-level) organizes, evolves and manages its network topology, dynamics, behaviors, function and so on are main tasks for network scientists, this will help to gain more insight into the Internet and enhance the network’s infrastructure, and will also contribute some ideas on commercial decisions making.
In 1998, Faloutsos et al.[1] was the first to prove that the Internet was a scale-free network topology. By considering the Internet as a complex system, Park et al.[6] studied aspects of self-similar traffic, power-law connectivity, WLAN PHY lay dynamics and non-cooperative network games. Ma et al.[7] proposed a macroscopic network-aware model which demonstrated the interactions and also the characteristics of the application and network providers. Their study observed the origin of the Internet’s evolution and the factors affecting this. Most Internet evolution studies are based on either the physical network layer or the logical topology layer. The studies of the physical network have mainly focused on the Internet’s economic ecosystem, especially the commercial relationships between ASes. For over a decade, researchers analyzed the AS-level Internet growth related to AS function and business relationship types.[12,13] Meanwhile, other studies were based on the logical topology layer applied the complex network theory. By analyzing the Internet’s evolution, some studies have verified that under the preferential attachment condition, the Internet topology was a scale-free network.[14,15]
While studies have succeeded in better understanding the evolution of the Internet, as of yet, no studies on the systematic behavior of the Internet have been done. Phases have changed in the IPv4 and IPv6 AS-level Internet evolution over a long period of time.[16] Ai et al.[17] observed sudden changes in the mean degree, the mean path length and other metrics of IPv6 in time series. Both of these studies only briefly worked on the fluctuation and mutation of the Internet, considering the Internet as a complex network. In 2006, Moore et al.[18] proposed models of the time evolution of networks, which were more practical, by adding and deleting nodes. This led to the realization that the essence of network evolution is the changes of nodes and edges in topology. Oliveira et al.[19] formulated the topology liveness problem and contrasted it with the completeness problem and developed an empirical model to characterize the trend of AS topology evolution. In a different network model, the edges between the new added node and the old node are allowed to change when new nodes are added to the network. The positive-feedback preference (PFP) model simulated the growth of the nodes and internal links, using the nonlinear preferential attachment mechanism.[8] Based on PFP, an evolving network model was proposed, with a description of birth and death of the nodes and edges to characterize the evolution of the AS-level Internet.[9]
It is known that nodes need to build connections with other nodes. The more connections that a node can get, the more robust it will be. Hence, some researchers have studied fundamental function-structures analyzing the subgraphs or components of a complex network.[20–22] Maslov[23] identified hierarchical features of the Internet topology to utilize topological pattern units. Topological patterns were used to detect network features and to identify a hierarchical feature of Internet topology. Kiremire et al. adopted a network component-based analysis approach to compare the schemes’ performances of the Internet topologies.[24]
In 1969, there were only four experimental nodes that were built as an early Internet. By 1983, this number had increased to 300 connected computers. Nowadays, the number of connected Internet devices is tremendous. The Internet is becoming a huge and complicated system that consists of tens of thousands of AS and billions of IP addresses.
The data applied in this study was obtained from the Border Gateway Protocol (BGP) router Table data, which was captured by three projects: Route–Views, RIPE NCC, and PCH. First, we downloaded the raw BGP probing data from the BGP router Table which contains the data from January 1998 to August 2013. Each day’s data are provided by all the probing monitors. Second, we merged the whole month’s daily data which is provided by all monitors into one snapshot of the Internet to represent the monthly snapshot. By merging data from all of the monitors, we could minimize data incompleteness, this is likely to be caused by equipment failures, hardware or software updating errors and untimely information aggregation. Third, by extracting the AS_PATH records and filtering the located data[23] from merged snapshot dataset files, 184 topologies in time series were obtained.
The AS_PATH field will identify the autonomous systems from the routing information, which is carried by the BGP messages. The components are extracted from AS_PATH: AS-CONFED-SEQUENCEs, AS-CONFED-SETs or AS-SETs. In summary, it is necessary to pass the data through this filter to get the neat and tidy Internet topology. More precisely, to improve validity, the following three steps are carried out to extract the AS_PATH field:
i) Compress AS_PATH paths. For example, the path “a-b-c-c-c-d” will be compressed to “a-b-c-d”. Once a BGP router sends an advertisement, it must add its own AS number (ASN) to the far left of the AS_PATH path. The BGP protocol allows self-ASN to be added onto the AS_PATH repeatedly to increase the length of the AS_PATH, and it will affect the routing decision of their neighbors’ routes.
ii) Filter the AS_PATH paths of the present loop. Generally, some of the BGP routing rules need to be manually set by an administrator. Thus, some errors could be produced, which will generate self-loops.
iii) Filter these AS_PATH paths, which are contained in AS-CONFED-SEQUENCE, AS-CONFED-SET, and AS-SET. The AS-SET path is disordered, and the AS in the AS-CONFED-SEQUENCE and AS-CONFED-SET belongs to local federations. Therefore, we need to filter out these three types of data and only adopt the AS-SEQUENCE data. Additionally, filter the AS_PATH paths, which contain any private AS. The RFC6996[25] has specified that AS64512∼AS65534 are private ASN. If an AS_PATH contains a private AS, then it apparently suggests that the routing information is wrong.
These pre-processing steps were used to decrease the noise and improve the validity of the data.
The Jaccard similarity theory, known as intersection over union and the Jaccard similarity coefficient, is a statistic that is used to compare the similarity and diversity of sample objects.[26,27] Inspired by Jaccard’s theory, to study the object’s evolutionary behaviors on a time-series, we focus on the changes that the system undergoes during its evolution and the dynamic evolution mechanism of the Internet. This is different from the classic methods of studying the evolution of the Internet, which have mainly investigated the phenomena and behaviors of the Internet. Based on set theory and Jaccard’s similarity theory, we designed a method to investigate the behavior of the Internet, by partially regarding the evolutionary process of the Internet as biological evolutionary process.
This paper uses the dynamic network G to model the process of evolution of the Internet over time. The relevant definitions are given below, and a glossary of terms and abbreviations used are given in Table
| Table 1. Glossary and abbreviation. . |

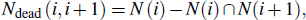 |
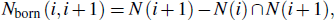 |
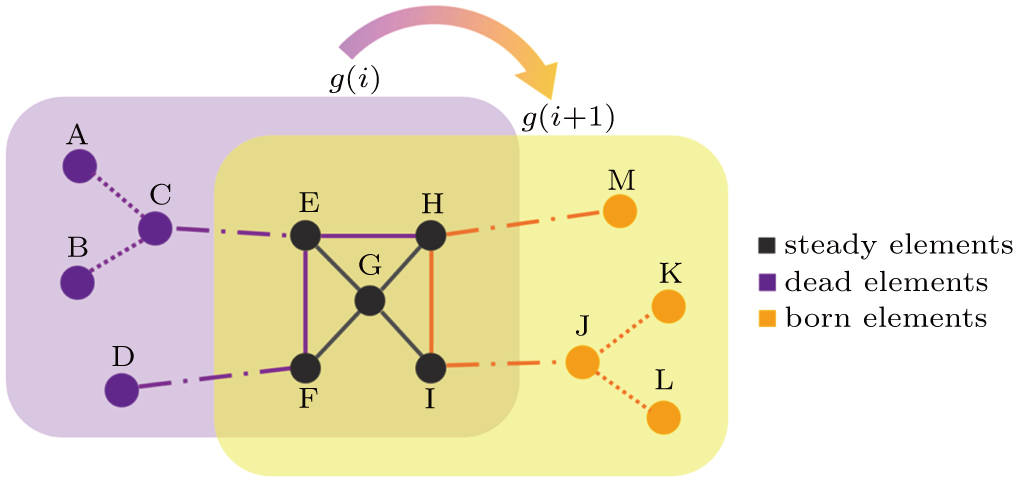
In some studies, the new-born nodes and dead nodes of the Internet IP-level network are treated equally, without considering the fact that some elements work together as one unit.[28,29] These cooperating elements contain up to three nodes, which are the most basic and fundamental elements after one singular node, so that each component consists of only two or three nodes and a few edges. A diagram of these three basic components (M1, M2, and M3) is shown in Fig.
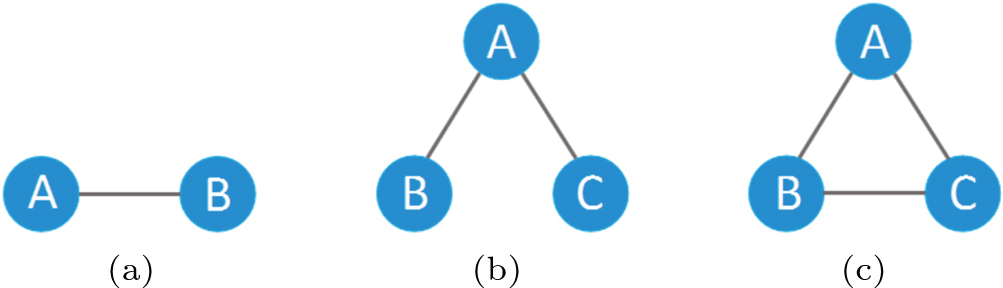 | Fig. 2. Graphs of 3 simple components in complex networks. (a) Single-edge component M1; (b) Binary component M2, with three nodes and two edges; (c) The triangle component M3. |

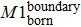
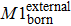

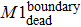
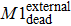

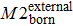

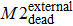
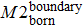
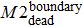
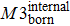
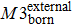

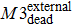
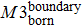
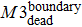
Researchers have modified a few entropy change formulas in various interdisciplinary applications.[30–33] To observe the system structure state during the evolution of the Internet, we selected one which depicts topological feature. The structural entropy of complex network was defined as in Eq. (
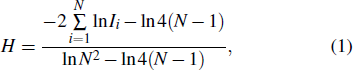 |
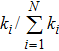
Communication networks, social networks, power grids, protein–protein interaction networks and neural networks can all be considered as complex networks consisting of a series of nodes and edges, on which signals and information can be transmitted from the source nodes to the target nodes by specific routing rules. The global topology of a complex network can influence the local information flow direction and the nodes’ load. Local changes can cause system fluctuation and lead to large scale network crashes due to a cascading failure reaction.
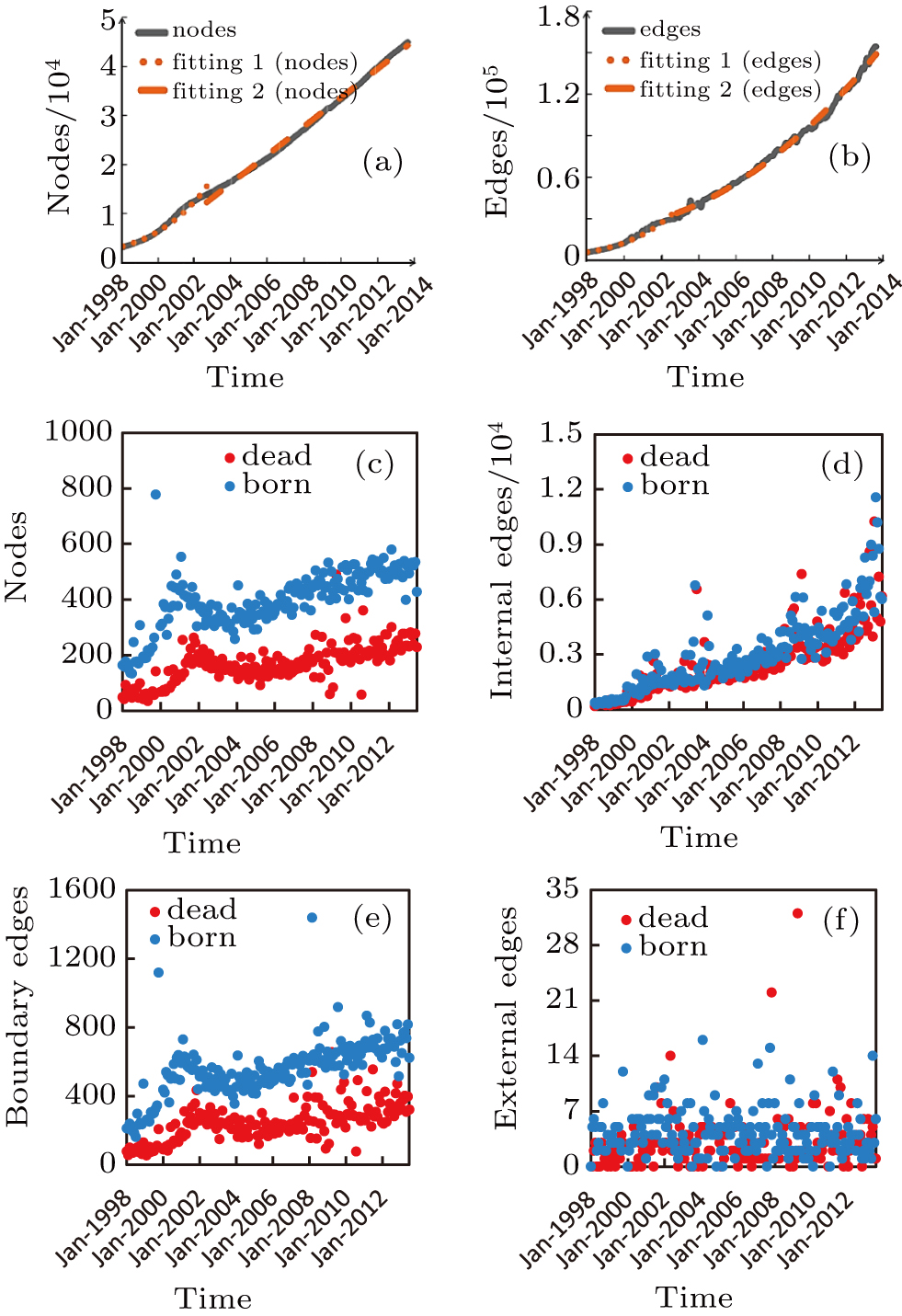
For example, with the development of the Internet, nodes and edges in the Internet have increased significantly. Figures
y = 2411.35* ex/25.34 + 631.75, where x is in the range of January 1998 to July 2003;
y = −92.43+244.89*. x, where x is in the range of January 2003 to August 2013.
In Fig.
y = 5099.52* ex/24.06 + 181.44, where x is in the range of January 1998 to July 2001;
y = 3.57* x2 + 18.93* x + 22190.24, where x is in the range of July 2001 to August 2013.
The regression models show the Internet global progress from a very simple topology with a few nodes and edges in 1998 to a fairly complicated topology with an enormous number of nodes and edges in 2013, they briefly show the trend of developments of nodes and edges of the Internet topology. The number of nodes and edges of the Internet have been increasing continuously (Figs.
We investigated the process of evolution of the birth and dead activities separately (Fig.
The 

To observe the overall growth of the network edges, an estimate of the mean birth rate is described by:
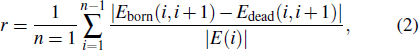 |
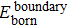
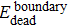
According to these results and the general principle of networking, an Internet evolution scenario is described as a newborn node usually builds connections (boundary edges) with one or more than one existing nodes first to join into the Internet system. Furthermore, some nodes are interconnected by external-edges which are added to the Internet at the same time. They then participate in the local restructuring activities by adjusting local connections. Although the nodes and edges are the basic elements of the complex network, the network components representing the function structures are more relevant to study the complex behaviors of the Internet’s evolution. Therefore, in the next section, we will investigate the evolution of network components.
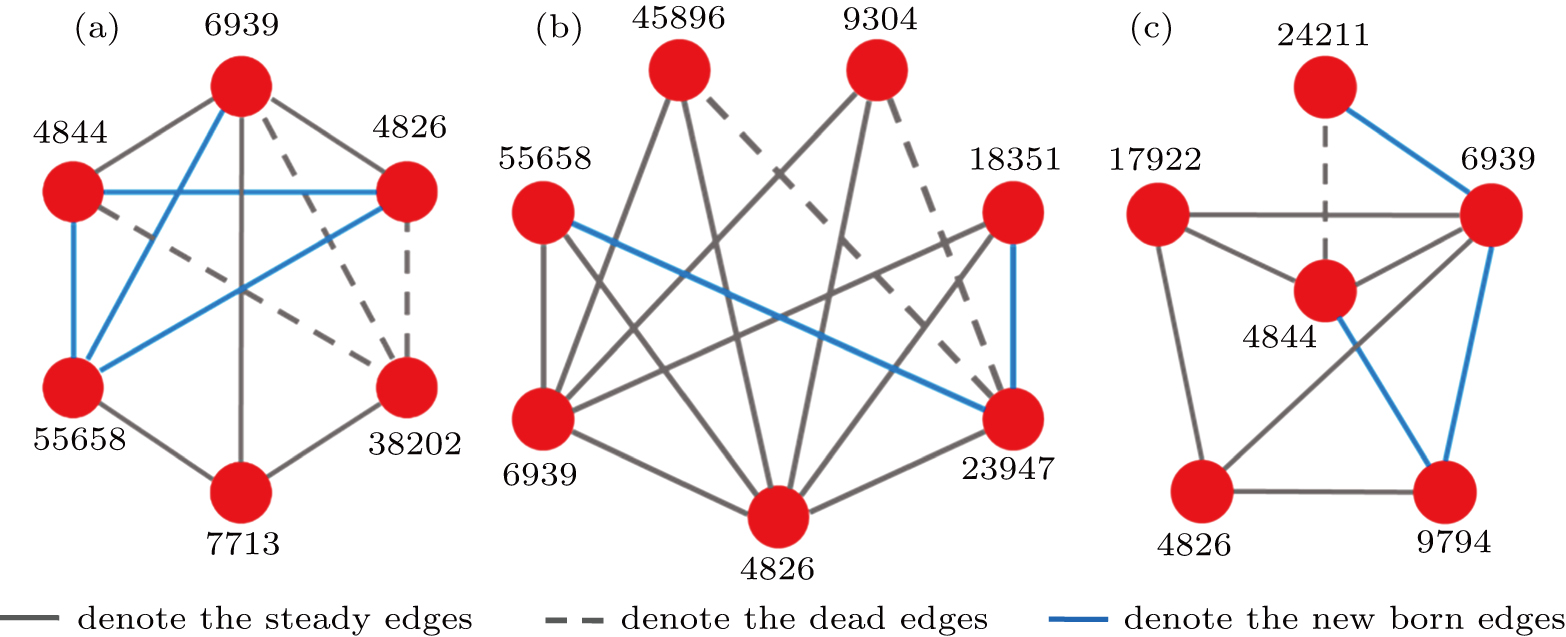
The internal-edges are the main factors governing the evolution of the Internet, while the effect of the two other types of edges is marginal. Therefore, whether the internal-edges will cooperate with other types of edges to co-build a network is of interest, such as by sharing common nodes. In other words, might the internal-edges participate to form any network components, while the boundary edges and external edges form the network components dynamically? How do those network topology components evolve? A router cannot establish the connections with an unlimited number of routers instantly and the old Internet architecture cannot adapt to the modern technology. Therefore, network administrators have to change the old Internet architecture or the local network connections to improve the Internet’s efficiency. This is a scenario of network component reconstruction, and the reality becomes even more complicated. This study simplified these complicated scenarios into the following procedure: Any changes within the network, either addition or removal of nodes, edges or components, will break the system’s equilibrium. However, the system itself will strive to maintain equilibrium by adding or removing some certain elements. Our work investigated three particular types of network component, M1, M2, and M3; as shown in Fig.
Table
So far in this study, the Internet’s activities are analyzed from the node level, the edge level, and the component level. During the evolution of the Internet, the whole topology structure adds new nodes, whilst components are formed to reconstruct the system topology. Table shows that components are added into and removed from the Internet at the same time to keep the system equilibrium. For example, both the birth and death of elements can cause the system to diverge from equilibrium. The system reacts as a self-organizing system[25] to maintain the equilibrium, by adding or removing certain elements. Although it is impossible to distinguish whether birth will precede death, is there a correlation between components’ births and deaths? To answer this question, the details of the Internet reconstruction are studied as follows.
| Table 2. The evolution activities of network components M1, M2, and M3. . |
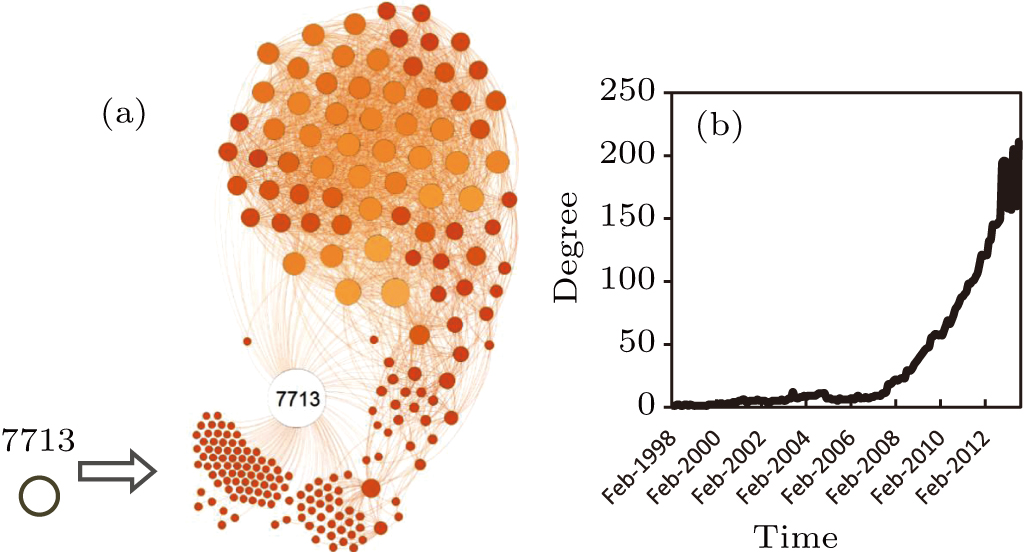
To address this problem, an analogy is put forward to depict the process of evolution from a single node. One newborn node is like an infant growing up and making friends with other nodes over time, encountering some anomalies and being restrained by the surroundings. In this process, the system allows its participants to involve in the topology by using materials that already exist. A few of these new nodes may disappear after a short time but most of them will continuously participate in the “life-sustaining” process (which can also be called metabolism) within the network’s topology. In this process, some of them even become important or fundamental members (nodes) of the network. Inspired by this analogy, we observed and analyzed the evolutionary process of node AS7713 (AS7713 represents the autonomous system number of a single administrative entity or domain whose information is registered in the RIR). Once AS7713 was added into the Internet in January 1998, its degree grew exponentially after October 2004 (Fig.
In Subsection
Figure
The equilibrium of the Internet can be disturbed by either the growth of nodes and edges, or reconstruction of the network components. As a complex system, changes of network nodes, edges, and components are the essential activities of the Internet. We wondered if those essential behaviors will change the basic characteristics of the Internet system. Therefore, we attempted to investigate it from the view of global Internet topology. The Internet is a typical complex network with scale-free characteristics,[8] where the degree distribution follows the power law, p(k) ∼ kγ (k is the degree of the nodes in the network. For scale-free network, the γ value is typically in the range [2, 3], although it may occasionally lie outside these bounds, in a number of real world networks it has values between 1.2, 2.9). Power-law values γ of degree distributions of all the sampled networks are in the range [1.78, 2.25] and the standard deviation is 0.13. The degree distribution of the AS-level Internet network appears to follow a power law. The scale-free features of the network are relatively stable, which refers to the growth process and attachment preference have not been changing much over time.
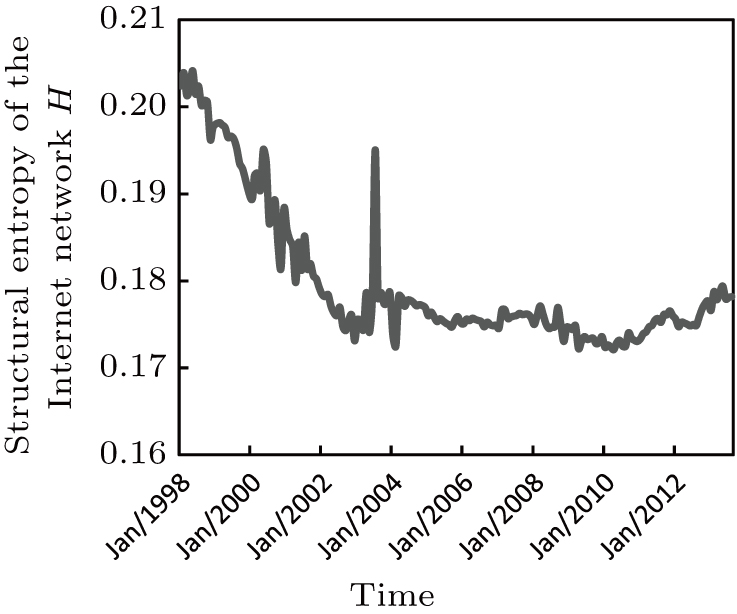
Figure
From April 2003 to August 2013, the value of H of the Internet remained within the range of [0.1725, 0.180]. The tendency of the fluctuation is slow and smooth. It is worth noting that from 2000 to 2003, the Internet experienced a historic speculative bubble when the stock markets in industrialized countries saw their equity value rise rapidly due to growth in the Internet sectors and related fields.[39] Before 2003, the Internet Service Providers (ISPs) expanded the Internet infrastructure tremendously to meet the massive needs of Internet companies. After the Internet bubble, the Internet’s resources were in excess because a large number of Internet companies went bankrupt. To decrease the operating costs and to improve the efficiency of network transmission, some ISP companies chose to merge with each other, while other companies optimized their self-network topology to provide better network services. No matter which strategy was chosen, the companies could not change the fact that the Internet topology had made a response to the surrounding environment. The Internet structural entropy decreased linearly from January 1998 to March 2003 (Fig.
The birth and death of network nodes, edges and component structures are an external expression of the Internet’s metabolism. Our network evolution analysis considers the birth and death of network entities during the network growth process. The aims of this paper were to detect the Internet’s evolutionary process from nodes-level, edges-level, and components-level, and precisely distinguish them into internal, boundary, and external units. Table
The facts that we observed in evolutionary process of the Internet can be summed up as follows: first, as a complex system, the Internet presents some complicated characteristics, such as self-organization, scale-free and synergetic. Inspired by the behavioral dynamics of biological groups, the process of the Internet evolution was found similar to some phenomena of biological evolution, such as metabolism and replication. For example, the growth of nodes and edges is comparable to biological metabolic activities. In biology, metabolism is a term that is used to describe all of the chemical reactions involved in maintaining the living state of the cells and organisms. It is usually divided into two categories: catabolism (the breakdown of large molecules to smaller molecules in order to obtain energy) and anabolism (a set of constructive metabolic processes, aimed to synthesize complex molecules). The node and edge entities can be seen as the metabolites during the growth process of Internet. We also suggest that the reconstruction of network components (the self-replicative process of the Internet system) is comparable to replication. Since the resources that it uses to construct the topology are replicas of itself, the new topology is built up by rearranging and connecting them in new position or location. As an analogy, viruses can replicate but only by taking advantage of cell reproduction through a process of infection. Harmful prion proteins can replicate by converting normal proteins into rogue forms. Similarly, computer viruses use an approach in that they reproduce using the hardware and software already present on computers.
With the continuous growth of the Internet’s network, the number of nodes increases while the evolution of the edges enhances the function of the Internet and increases the complexity of its topology. This study shows that the evolution of network edges, especially that of internal edges, is the dominant force that drives the evolution of the Internet. The Internet network mainly consists of internal components, particularly M2 internal components. Newborn nodes primarily build multiple connections with existing nodes, while most of the dead nodes fall off from the edge of the network. It is noteworthy that during this evolutionary process, the Internet increased in size and became more efficient, and so on, but did not change the attachment preference and has remained in a stable state (in terms of the hierarchical structure of the Internet architecture) since 2003. The evolution of the Internet is governed by a principle according to which the network topology evolves towards increasing complexity.
By deconstructing the network topology into components, we make a preliminary study on the Internet’s evolution considering the reconstruction of the three simplest functional components, namely: M1, M2, and M3. However, further work is needed to gain a better understanding of how more complicated components, such as those consisting of four, five or even six nodes, participate in the evolution of the Internet. Apart from this study on metabolism and replication of the Internet, an observation of the mutation and selection processes within the Internet’s evolution would be of interest. In addition, this study will make viewing some of the large scale-properties of the Internet in light of general biological laws acceptable. Although different in certain aspects, the Internet has many similarities with biological intelligence. Consequently, this paper makes an effort to recognize the life phenomena in this artificial complex system.
Moreover, it would be of interest to model metabolism or to use the underlying principles in comparable evolutionary processes to make a comparison between the Internet and biology. This would enable us to predict the outcomes and future use of the Internet. We are currently taking a further observation of AS7713’s (a hub) development and interactive activities, and we look forward to seeing some new results which would be of interest.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] | |
| [39] |