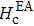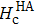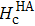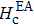† Corresponding author. E-mail:
Project supported by the National Basic Research Program of China (Grant Nos. 2015CB921403 and 2016YFA0300701), the National Natural Science Foundation of China (Grant Nos. 51427801, 11374350, and 51671212), and the Chinese Government Scholarship (Grant No. 2015GXYG37).
The uniaxial magnetic anisotropy of obliquely deposited Fe(001)/Pd film on MgO(001) substrate is investigated as a function of deposition angle and film thickness. The values of incidence angle of Fe flux relative to surface normal of the substrate are 0°, 45°, 55°, and 70°, respectively. In-situ low energy electron diffraction is employed to investigate the surface structures of the samples. The Fe film thicknesses are determined to be 50 ML, 45 ML, 32 ML, and 24 ML (1 ML = 0.14 nm) by performing x-ray reflectivity on the grown samples, respectively. The normalized remanent magnetic saturation ratio and coercivity are obtained by the longitudinal surface magneto-optical Kerr effect. Here, the magnetic anisotropy constants are quantitatively determined by fitting the anisotropic magnetoresistance curves under different fields. These measurements show four-fold cubic anisotropy in a large Fe film thickness (50 ML) sample, but highly in-plane uniaxial magnetic anisotropies in thin films (24 ML and 32 ML) samples. In the obliquely deposited Fe films, the coercive fields and the uniaxial magnetic anisotropies (UMAs) increase as the deposition angle becomes more and more tilted. In addition, the UMA decreases with the increase of the Fe film thickness. Our work provides the possibility of manipulating uniaxial magnetic anisotropy, and paves the way to inducing UMA by oblique deposition with smaller film thickness.
Magnetic anisotropy may be of technical importance for the application of magnetoresistive (MR) devices. It has been recognized that higher perpendicular magnetic anisotropy is desirable for future high-density magnetic recording (HDR) and high frequency magnetic devices. For various devices in the magnetoresistive random access memory (M-RAM) and the hard disk drive (HDD) head component, an in-plane magnetized film with a uniaxial anisotropy is being used.[1]
The oblique deposition of magnetic films can effectively induce a highly in-plane uniaxial magnetic anisotropy.[2,3] In an obliquely-deposited ferromagnetic film, the coercive field increases sharply as the deposition angle becomes more and more tilted. In addition, there is a steep transition between magnetization directions when measured along the easy axis of the structures, leading to a very square hysteresis loop. The evaporation of Co and Co alloys onto the polymer substrate has been used to produce medium for high-density magnetic recording tape.[4] In oblique deposition, magnetic anisotropy is usually associated with shadow and steering effect, resulting in elongated grain structures or ripples on a nanometer scale. These elongated grain structures and ripples give rise to in-plane uniaxial magnetic anisotropy.[5–8] The anisotropic surface roughness of obliquely deposited Ta, Pt, or Co underlayers also causes highly uniaxial magnetic anisotropy.[9–12] While in the magnetic films deposited at normal incidence, the magnetostatic coupling arising from the anisotropic undulation of the interface between the underlayer and the magnetic film causes in-plane magnetic anisotropy.[13] Previous reports have shown that in Pd/obliquely deposited Fe/Al2O3(0001), despite the existence of protective Pd overlayer and insulating Al2O3(0001) substrate, the obliquely deposited Fe film still shows an explicit uniaxial magnetic anisotropy energy.[14] In recent years, the interfacial magnetic anisotropy and coercive field have been studied in many systems including 3d magnetic metal covered by non-magnetic films.[15–18]
Up to now, different characterization tools have been used to measure magnetic anisotropy constants, such as ferromagnetic resonance (FMR),[19] hysteresis loop measurement, torque measurement,[20] rotating magneto-optical Kerr effect (ROT-MOKE),[21] and transverse biased initial inverse susceptibility and torque (TBIIST).[22] For ultra-thin films, coherent domain rotation magnetization reversal does not always occur, particularly when the applied field is lower than the saturation field. Therefore, it is a challenge to accurately determine the magnetic anisotropy constant from the magnetization hysteresis loop. Anisotropic magnetoresistane (AMR) was therefore considered as an accurate technique for magnetic anisotropy measurement in thin films.[23–28] In order to ensure a real single domain rotation, an appropriately large field is required.
The Fe/Pd is an excellent candidate for studying the relationship between atomic structure and magnetism in low dimensional heterostructures. In the past, most of the work has been carried out on the growth behavior and structure of Fe thin films deposited on MgO(001) substrates.[29–36] However, the magnetic properties of Fe films on MgO(001) substrates still need to be studied in more detail. In this paper, we report the magnetic behavior of Fe film obliquely deposited on MgO(001) substrate as a function of deposition angle and film thickness. The magnetic properties are measured by azimuthal rotation through ex-situ magneto-optical Kerr effect (MOKE) at room temperature. In addition, the magnetic anisotropy constants are quantitatively determined by using the standard four-point method of anisotropic magnetoresistance (AMR) measuring setup.
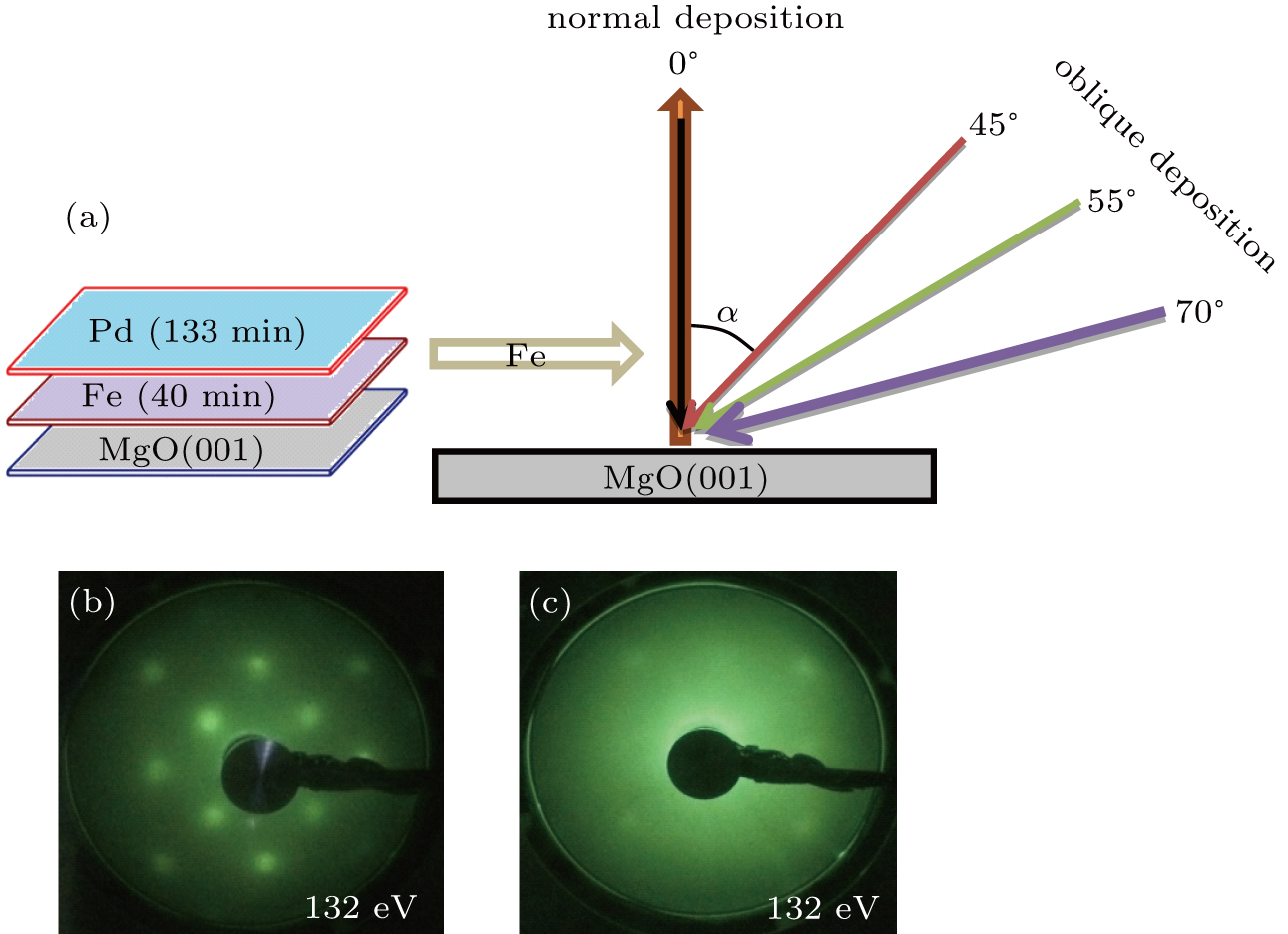
The Fe films were deposited on cleaned MgO(001) substrates by molecular beam epitaxy (MBE) in an ultra-high vacuum (UHV) system with a base pressure of 2.0 × 10−10 mbar. The MgO(001) substrate had been first heated at 700 °C for 2 h to remove the adsorbed gas from the surface before the film was deposited. The clean surface of MgO(001) was confirmed by in situ low energy electron diffraction (LEED) equipped within the Omicron UHV system. Subsequently, the Fe (99.995% purity) film was deposited on the MgO(001) substrate by the oblique-incidence deposition method. The Fe films with thicknesses of 50 ML, 45 ML, 32 ML, and 24 ML were obtained by varying the oblique deposition angle (α) relative to the normal surface of the substrate. The Fe film deposition angles (α) were 0°, 45°, 55°, and 70°, respectively. The growth time of Fe film for all samples was kept the same (i.e., 40 min) in the deposition processes. Therefore, the deposition rate of Fe film was 0.6–1.25 ML/min, while the substrate was still kept at room temperature. Before taken out of the UHV chamber, all samples were covered with a layer of ∼ 6 nm Pd, normally deposited under pressure of 5.0 × 10−9 mbar. Figure
in situ low energy electron diffraction (LEED) equipped within the Omicron UHV system was employed to investigate the surface structure of the samples. The x-ray reflectivity (XRR) was performed to determine the film thickness and roughness for all samples by a Bruker D-8 x-ray diffractometer using Cu Kα radiation (λ = 0.15405 nm). The ex-situ longitudinal MOKE measurements were carried out at room temperature and described elsewhere.[37,38] In addition, the magnetic anisotropy constants were determined quantitatively by fitting the angle-dependent anisotropic magnetoresistance (AMR) curves. The home-made AMR setup consists of a Wheatstone bridge, a lock-in amplifier (Stanford Research Systems SR830 DSP), and a rotational magnetic stage around a stationary sample. In the experiments, a sufficiently large and stable field was used to guarantee a true single-domain behavior of the specimen. The sample size was 10 mm × 3 mm × 0.5 mm for AMR measurements, which were performed with a standard four-point method.
Figure
The XRR usually can be performed on the grown sample to determine the film thickness, roughness, and density. Figure
 | Fig. 2. (color online) X-ray reflectivity spectra recorded on 0°-Fe(001)/Pd thin film, with fitting parameters accurately determined by simulating (red line) the experimental curve (open circles). |
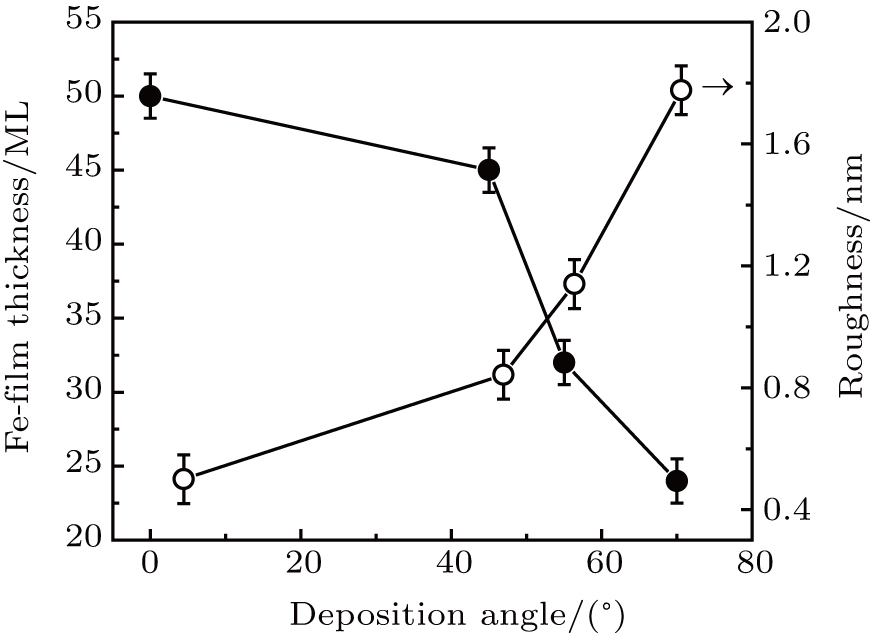 | Fig. 3. X-ray reflectivity measurement of Fe-film thickness (tFe) and roughness (σ) as a function of deposition angle α. |
| Table 1. X-ray reflectivity measurements of film thickness and roughness. . |
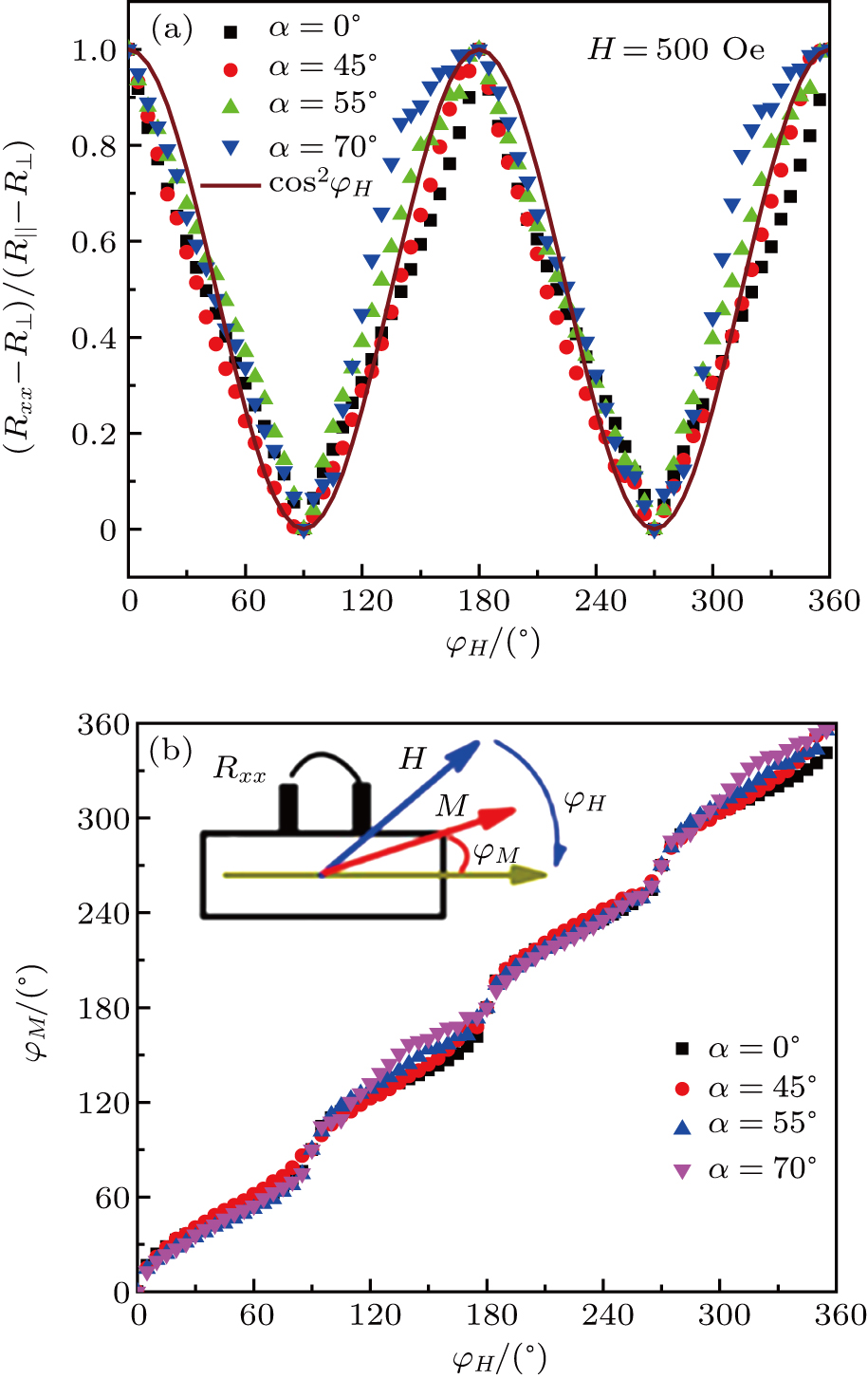
The magnetic properties are measured by azimuthal rotation through the ex-situ MOKE at room temperature. Figure
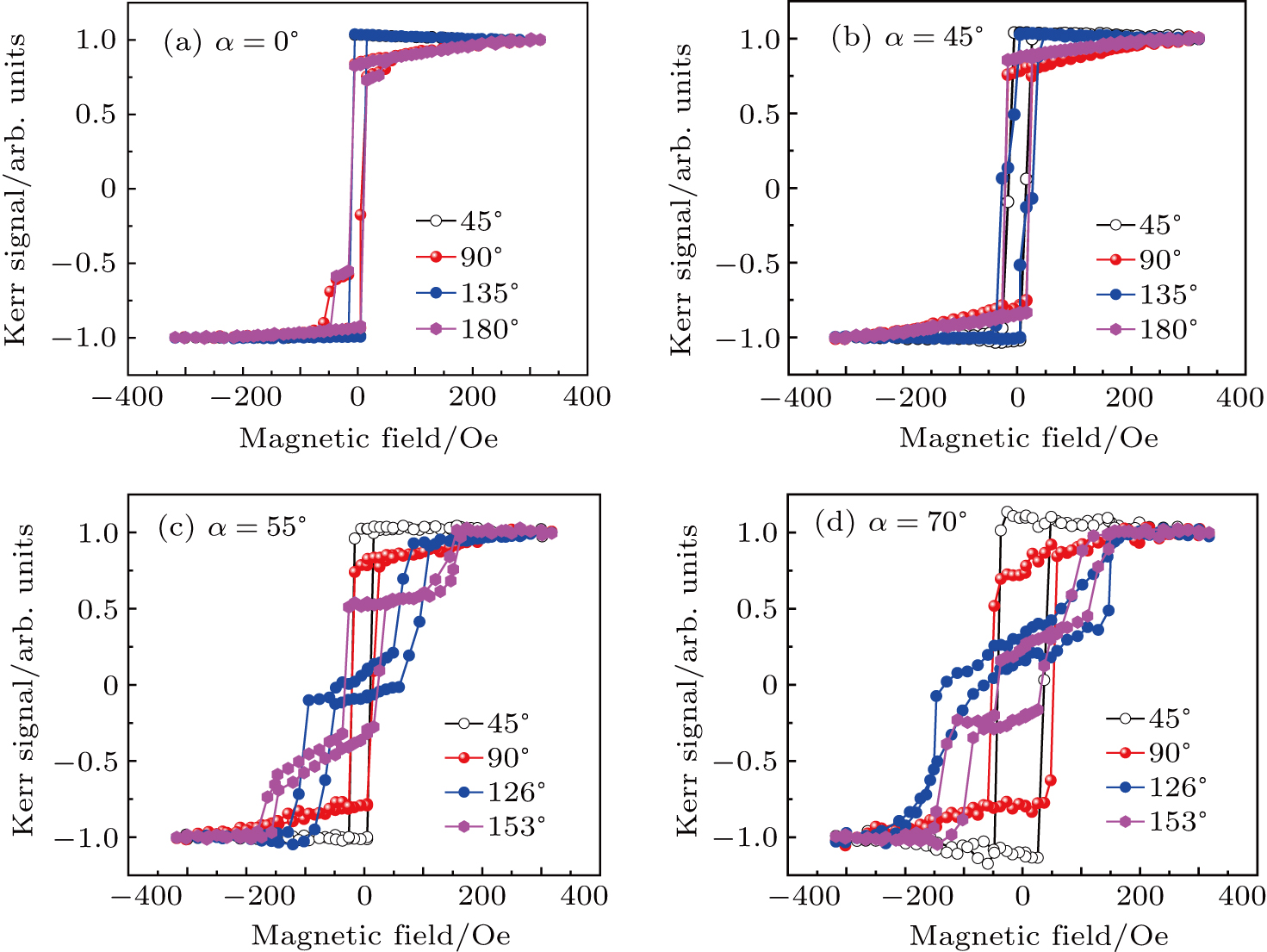 | Fig. 4. (color online) Typical magnetic hysteresis loops of Fe films at different deposition angles: (a) 0°, (b) 45°, (c) 55°, and (d) 70°. |
Therefore, on the contrary, our results show that the origin of the magnetic anisotropy is not the interface effect, nor the bulk property of the Fe layer, but it may be caused by the thickness of the Fe film changing with the oblique angle in the deposition process. The experimental dependency on the field direction of the coercive field (Hc) is plotted in Fig. 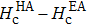
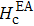
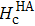
 | Fig. 5. (color online) Experimental dependency on the field direction of coercive field (Hc), with the same data plotted in polar coordinates in the inset. |
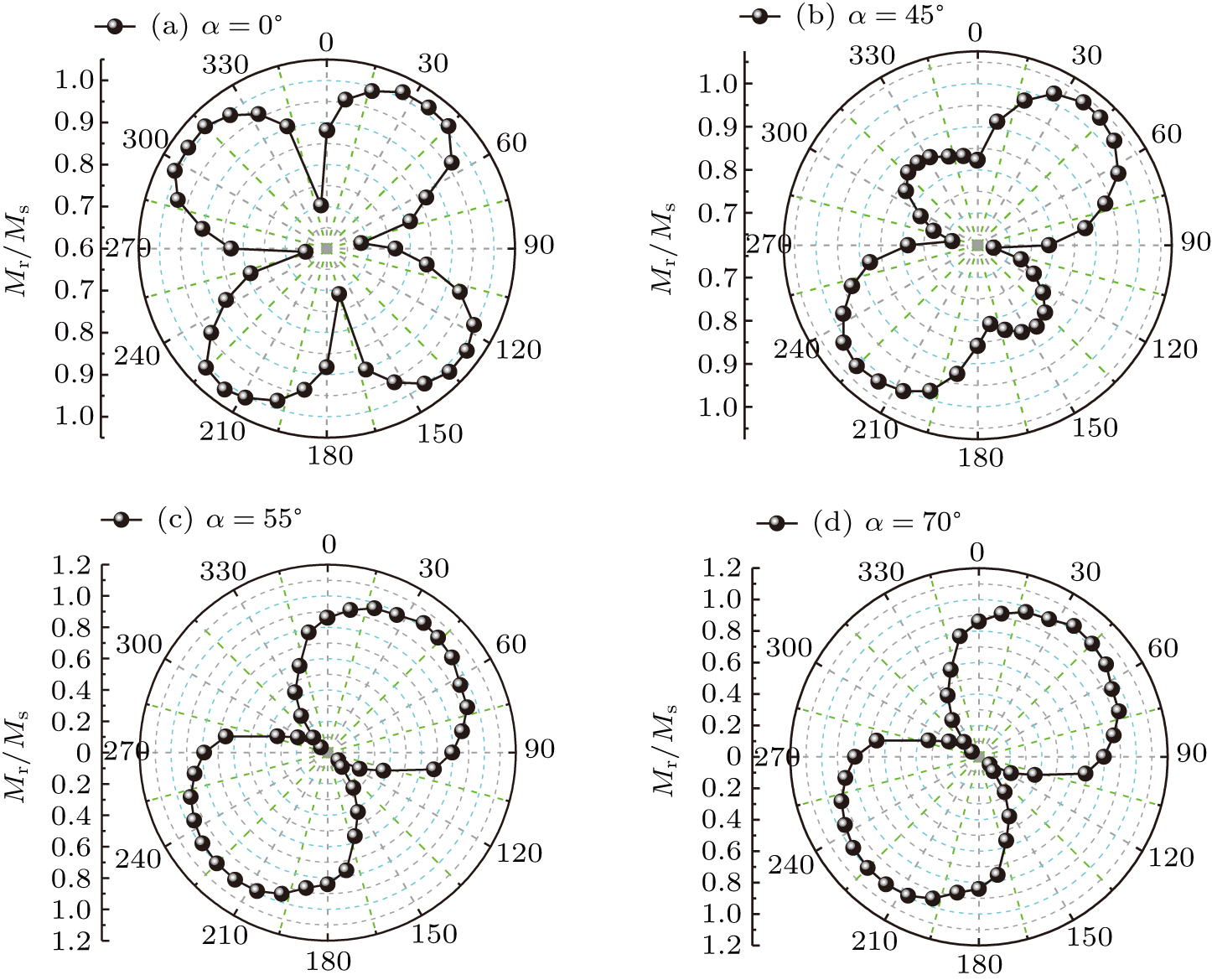 | Fig. 6. Angular dependent normalized residual polar plots of longitudinal MOKE data for all four samples. |
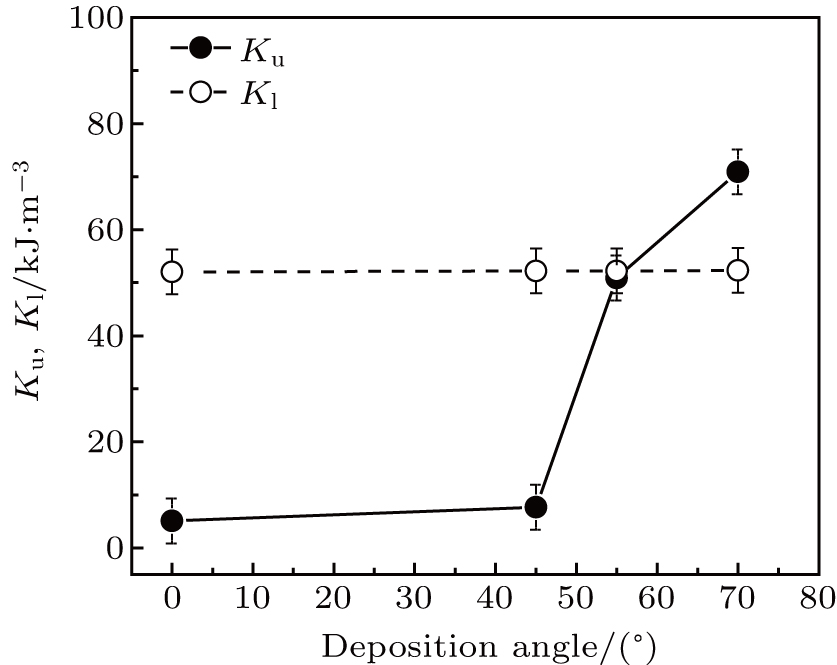
| Table 2. Magnetic anisotropy constants (Kl and Ku) and coercivity field (Hc) measured by using torque curves and MOKE, respectively. . |
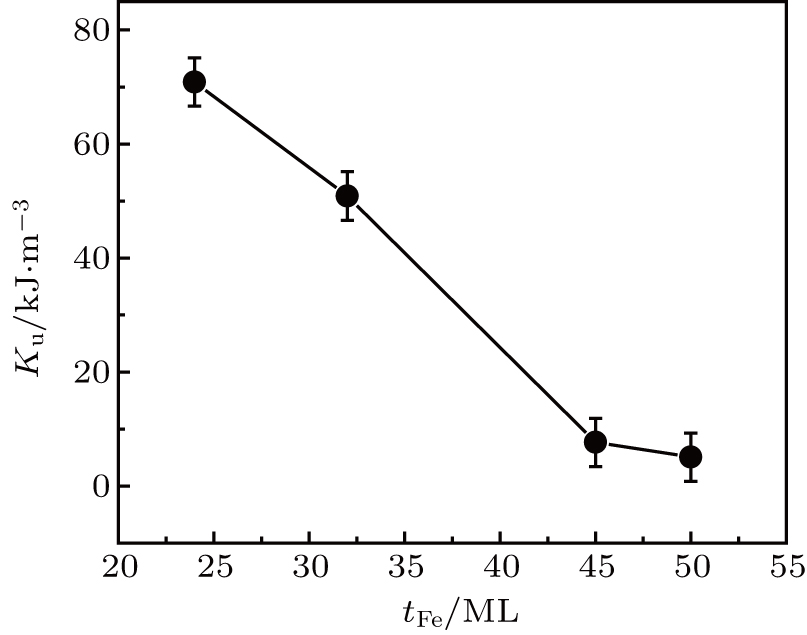
In order to quantitatively determine the constants of magnetocrystalline anisotropy Kl and uniaxial magnetic anisotropy Ku for all four samples, the torque curves are obtained.
The resistance in ferromagnetic metallic film is a function of angle φM, which is the angle between the magnetization and current (inset of Fig.
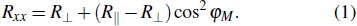 |
For real single domain rotation and excluding ordinary magnetoresistance effect, it is necessary to impose a higher external magnetic field than the saturation field.
The AMR curves of all four samples are plotted in Fig.
 |
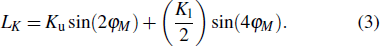 |
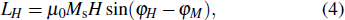 |
In order to compare the above two types of torques, the normalized torque is introduced below
 |
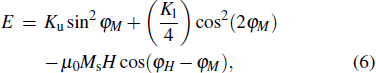 |
 |
The normalized magnetic torque curves for all four samples are shown in Fig.
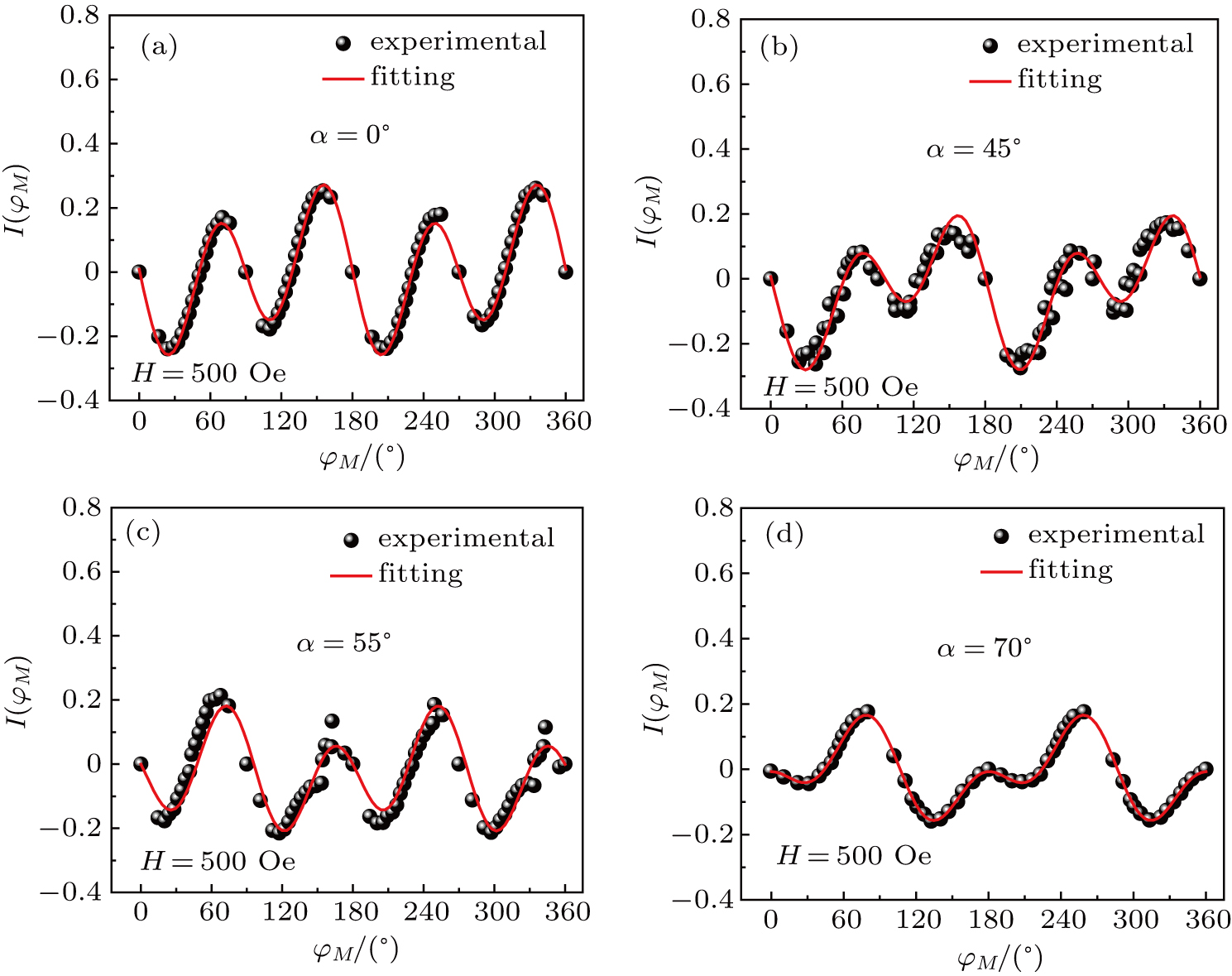 | Fig. 8. (color online) Normalized magnetic torque curves of Fe films deposited on Mg(001) substrate at different deposition angles: (a) 0°, (b) 45°, (c) 55°, and (d) 70°. |
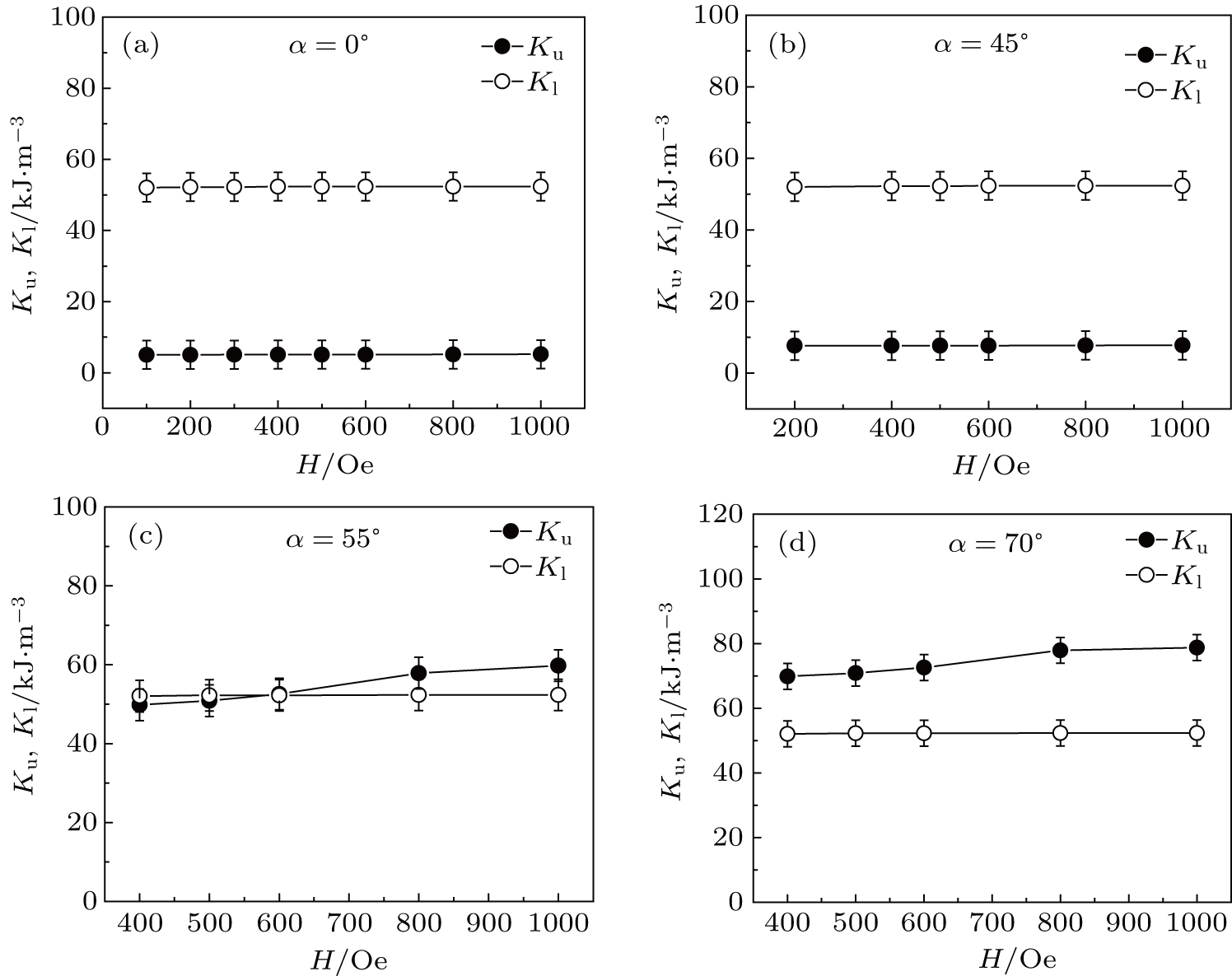 | Fig. 9. Anisotropy constants Ku and Kl versus applied magnetic field (H) of Fe thin films deposited at different deposition angles: (a) 0°, (b) 45°, (c) 55°, and (d) 70°. |
In this work, our measurements show four-fold cubic anisotropy in thick Fe film (> 32 ML) and superimposed highly in-plane uniaxial magnetic anisotropy in thin film. The in-plane UMA Ku induced by oblique deposition shows an increasing behavior with the deposition angle while Kl shows an invariant behavior. The values of MCA constant Kl and UMA constant Ku each exhibit almost a linear behavior with the applied field. In addition, the UMA Ku decreases with Fe film thickness increasing. The higher oblique deposition angle also results in higher coercivity.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] | |
| [39] | |
| [40] | |
| [41] | |
| [42] | |
| [43] | |
| [44] | |
| [45] | |
| [46] | |
| [47] | |
| [48] | |
| [49] | |
| [50] |