† Corresponding author. E-mail:
We briefly introduce a new high-pressure transport measurement system integrated with low temperature and magnetic field that is being established as one of the user experimental stations of the Synergetic Extreme Condition User Facilities in the Huairou District of Beijing, China. To demonstrate the capabilities of the system for condensed matter research, the emergence of some pressure-induced phenomena and physics related to superconductivity found previously is also introduced, and then a perspective for such an advanced high-pressure system is presented.
In the research frontiers of condensed matter physics, high pressure is widely adopted as an independent control parameter that can effectively tune crystal and electronic structures and consequently create a variety of new phenomena, which dramatically promote the finding of new materials, through the change of the atomic distance of matter. Consequently, high-pressure research is considered to be a new dimension in condensed matter physics.[1] Remarkably, a great deal of success has been achieved by the application of pressure in the studies on condensed matter, such as converting matter from an insulating or a semiconducting state to a metallic state,[2–7] and from a magnetic state to a nonmagnetic one.[5–9] Pressure-induced superconductivity and enhancement of superconducting transition temperatures (TC), as well as related phenomena, have been frequently found over a broad range of materials.[7–18] Noticeable are pressure-induced superconducting transitions in compressed elements of sulfur, oxygen, iron, lithium, and black phosphorous[11,19–22] and in complicated compounds of AFe2As2 (where A = Ca, Sr, Ba, or Eu).[23–26] Compelling examples of pressure-enhanced TC in known superconductors have been observed in the families of copper oxide (cuprate) and iron-based superconductors; for instance, the TC of mercury-bearing cuprates with a value of 134 K at ambient pressure is pushed up to 164 K at ∼ 30 GPa, which holds the highest TC among all copper oxide superconductors.[27–30] The TC of LaO1−xFxFeAs with a value of 26 K at ambient pressure has been also enhanced to 43 K at ∼ 4 GPa.[18,31] The simplest compound superconductor, FeSe, with the TC value of ∼ 8 K at ambient pressure,[32] has been found to jump to 36.7 K at 8.9 GPa.[17]
Meanwhile, pressure-induced phenomena and physics have emerged in the field of superconductivity research. Exciting research progress has been made, such as the observation of superconductivity with a transition temperature of > 200 K in H3S,[15,33–35] the reemergence of superconductivity in heavy-fermion and alkaline iron selenide superconductors,[8,36] the appearance of a bi-critical point in compressed Ca0.73(La0.27)FeAs2,[37] and superconductivity in Weyl semimetals.[38–40]
In this article, we first introduce the capabilities of our high-pressure transport measurement system and then present some experimental results achieved by high-pressure research for demonstrating possible applications of the system. Because of the limitation of the article length, it is not possible for us to cover all the important achievements in high-pressure studies on condensed matter in this review; therefore, we focus on some selected works from our research interests.
The system being established is one of the important equipment of the Synergetic Extreme Condition User Facilities (SECUF). The system integrates three extreme conditions, including high pressure (HP), low temperature (LT), and magnetic field (MF), as described in Fig.
It is known that a static pressure up to 100 GPa or even higher can only be realized by using a diamond anvil cell (DAC), which is the dominant device for achieving very high pressures in laboratory. Therefore, a DAC is adopted to generate high pressure for the system. In a DAC, the two anvils are placed oppositely, as shown in Fig.
The capacities of the system are shown in Fig.
Finding exotic phenomena and physics in condensed matter and understanding the underlying physics have long been research frontiers of condensed matter physics, among which superconductivity is a leading research field. The common variables, pressure, temperature, and magnetic field, have been broadly adopted as effective methods to tune crystal and electronic structures, making great contributions to the field of condensed matter physics. The emergence of phenomena in compressed matter leads to deeper insight into the underlying physics. Here, we will introduce some typical results achieved in high pressure studies on conventional and unconventional superconductors.
The discovery of cuprate high-temperature superconductors impacted science and technology considerably and the excitement in this field has been continuing for the past 30 years. To date, more than two hundreds of cuprate superconductors have been found,[41] among which HgBa2Ca2Cu3O8+x exhibits the highest TC up to 134 K at ambient pressure.[28] Many efforts have been made to push TC higher and the results have been documented in a long list. Pressure was found to play a key role in enhancing TC in this family. Most impressive is the application of pressure on HgBa2Ca2Cu3O8+x, enhancing its TC to 164 K at ∼ 30 GPa,[29,30] as shown in Fig.
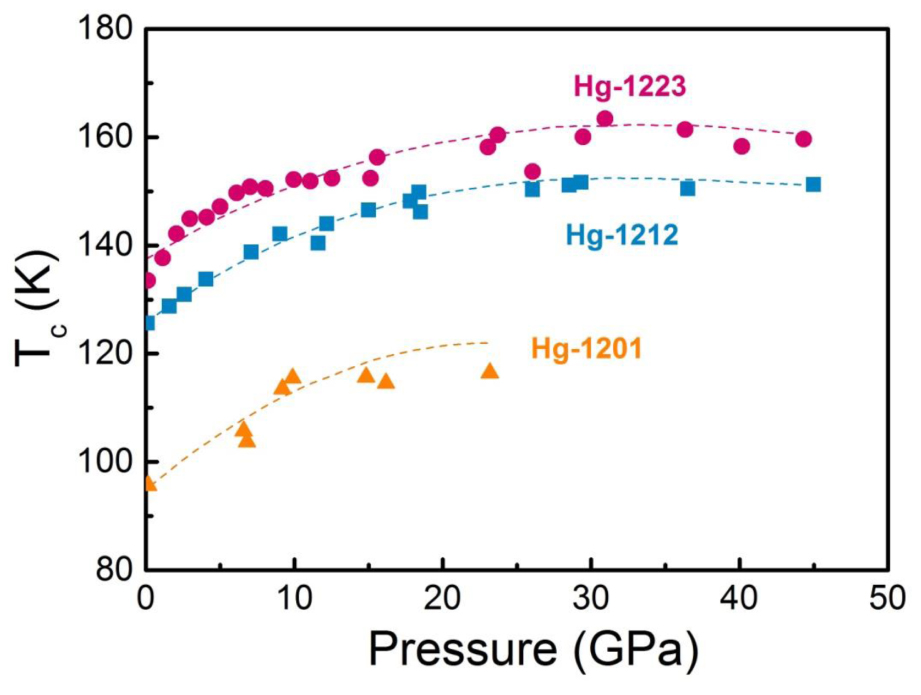 | Fig. 3. (color online) Pressure–temperature phase diagram of mercury-bearing cuprate superconductors, showing a TC up to 164 K. The data are taken from Ref. [29]. |
The discovery of LaFeAsO1−xFx superconductors with a TC of 26 K in 2008[31] brought new excitement to the field of superconductivity and sparked intense research activity in the past 10 years. Many research groups have made great advances in understanding this new kind of high-TC superconductor with the apparent hope of gaining insight into the underlying superconducting mechanism.[42–48] There are more than 15,000 papers that have been published so far.[48]
Pressure as a ‘clean way’ plays a prominent role in the search for Fe-based superconductors with higher superconducting transition temperature. High-pressure resistivity measurements of LaFeAsO1−xFx in a DAC revealed that its TC can be increased to 43 K at ∼ 4 GPa,[18] as shown in Fig.
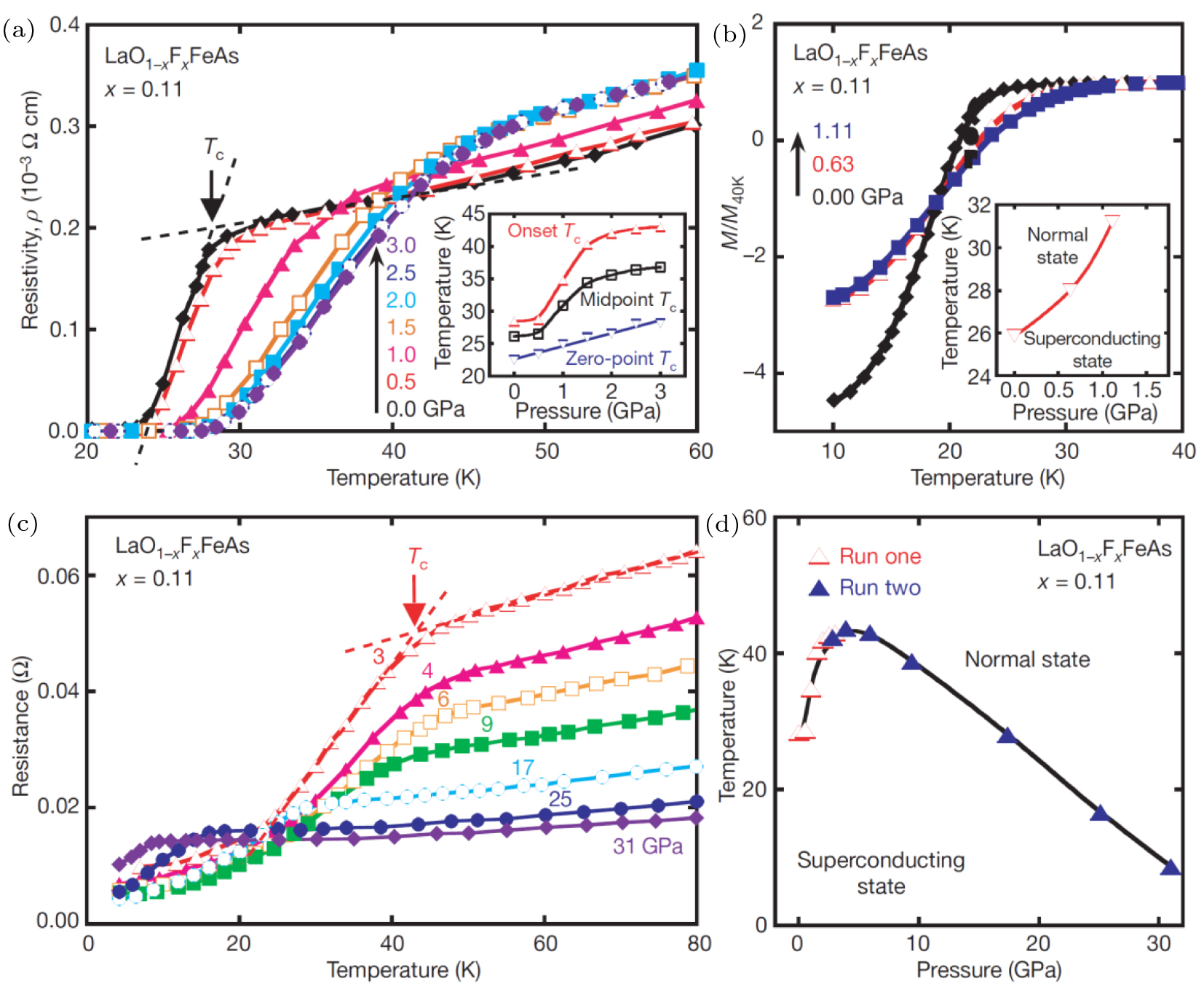 | Fig. 4. (color online) Superconducting properties in compressed LaO0.89F0.11FeAs. (a) Results obtained from measurements in a piston–cylinder pressure device (b) Magnetic dependence of TC under pressure. (c) Results obtained from measurements in a DAC, showing pressure-induced enhancement of TC in the superconductor. (d) Pressure–temperature phase diagram. Reproduced with permission from Ref. [18]. |
Because parent compounds were found in one of the subsystems of FeAs-based superconductors, whose chemical formula is A′Fe2As2 (where A′ = Ca, Sr, or Ba) and EuFe2As2,[56–59] this provides an opportunity to identify the effect of pressure in developing superconductivity and the correlation between the magnetic ordered state and the superconducting state in this new type of superconductor. High-pressure studies indicated that the superconductivity of these compounds is very sensitive to the pressure environments.[23–26,60–64] The physics behind this is considered to be associated with pressure-induced lattice distortion.[65–67]
More recently, high-pressure studies on the antiferromagnetic compound Ca0.73La0.27FeAs2 revealed unexpected phenomena: a first-order transition between antiferromagnetic (AFM) and superconducting phases and a bi-critical point at ∼ 3 GPa and 26 K,[37] as shown in Fig.
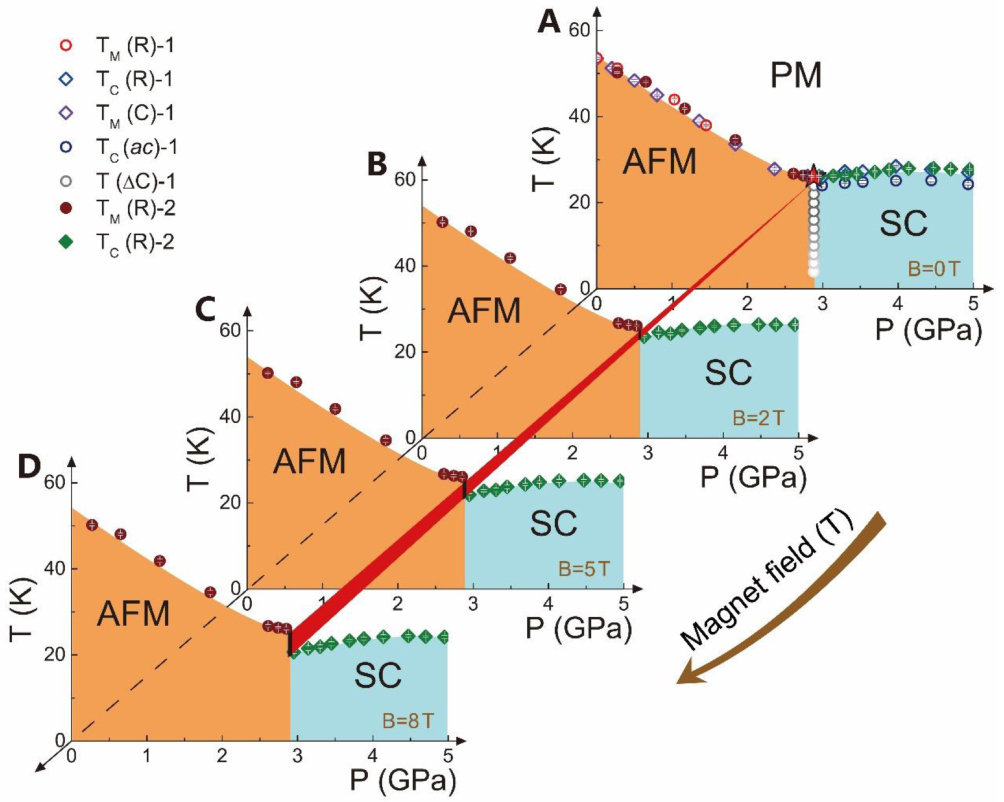 | Fig. 5. (color online) Temperature–pressure phase diagrams obtained at different magnetic fields for Ca0.73La0.27FeAs2 single crystals. The acronyms PM, AFM, and SC stand for paramagnetic, antiferromagnetic, and superconducting phases, respectively. The magenta-colored circles and custom diamonds represent the temperature of the AMF phase transition detected from two-run electrical resistance measurements (TM(R-1) and TM(R-2)) and heat capacity TM(C) measurements under hydrostatic pressure conditions. The green diamonds and blue circles stand for the superconducting transition temperature determined from the resistance TC(R-1) and ac susceptibility TC(ac) measurements, respectively. The position of the red star denotes the location of the bi-critical point, which is determined by an intersection of extrapolated lines of the pressure-dependent TM and TC. The gray circles are the data extracted from the heat capacity results. The radial red line shows the suppressed tendency of TC by the magnetic field. Reproduced with permission from Ref. [37]. |
An FeSe superconductor with a TC of 8 K was discovered by Wu’s group in 2008.[32] Surprisingly, the TC can be increased to ∼ 37 K at 8.9 GPa by application of pressure.[17] The pressure-induced dramatic enhancement of TC in FeSe was considered to be attributed to the pressure-driven increment of spin fluctuation.[68]
In 2011, alkaline iron selenide superconductors, A1−xFe2−ySe2 (where A = K, Rb, Tl/K, or Tl/Rb), with a transition temperature of ∼ 32 K were discovered,[69–72] adding a new subsystem to the family of Fe-based superconductors. The remarkable feature of these superconductors is that the superconducting (SC) phase coexists with an antiferromagnetic insulating phase (245 phase) in the microstructure, which is different from that of the other known FeAs-based superconductors.[31,46,51,73–75] Unexpectedly, high-pressure measurements on A1−xFe2−ySe2 (where A = K, Rb, Tl/K, or Tl/Rb) revealed that the pressure induces a second superconducting phase with a TC as high as 48.7 K after the first superconducting phase is suppressed by pressure,[36] as shown in Fig.
 | Fig. 6. (color online) Pressure–superconducting transition temperature (TC) phase diagram for Tl0.6Rb0.4Fe1.67Se2, K0.8Fe1.7Se2 and K0.8Fe1.78Se2. The symbols represent the pressure–temperature conditions at which TC values were observed from the resistive and alternating current susceptibility measurements; symbols with downward arrows represent the absence of superconductivity to the lowest temperature (4 K). All Tl0.6Rb0.4Fe1.67Se2, K0.8Fe1.7Se2, and K0.8Fe1.78Se2 samples show two superconducting regions (SC-I and SC-II) separated by a critical pressure at ∼ 10 GPa. NSC is the nonsuperconducting region at pressure > 13.2 GPa. The maximum TC is found to be 48.7 K in K0.8Fe1.7Se2 at a pressure of 12.5 GPa. At higher pressures > 13.2 GPa, the samples are nonsuperconducting. Error bars are one standard deviation. Reproduced with permission from Ref. [36]. |
Owing to the coexistence of the antiferromagnetic insulating and superconducting phases in these superconductors, pressure plays a unique role in revealing its intrinsic physics. To uncover the puzzling issues on the role played by the antiferromagnetic insulating phase in developing the ambient-pressure superconducting phase, comprehensive experimental measurements on the compound with a pure antiferromagnetic insulating phase and mixed phases (antiferromagnetic insulating phase plus superconducting phase) were performed. The results revealed two important issues: 1. the antiferromagnetic insulating phase is not the parent phase of the SC-II phase, and 2. it is a crucial phase for stabilizing the SC-I phase.[4,77,78]
The discovery of the first heavy-fermion superconductor, CeCu2Si2, by Steglich in 1979 not only imitated a new field for studies of unconventional superconductivity but posed a fundamental challenge for understanding the superconducting mechanism in a unified way.[79] Up to now, more than 40 heavy-fermion superconductors have been found.[80,81] Because most non-superconducting heavy-fermion compounds are antiferromagnetic, heavy-fermion superconductors belong to the family of unconventional superconductors.[8,81–85]
A general consensus held for unconventional superconductors is that the superconductivity develops in the vicinity of a suppressed AFM order state, thus, pressure can be used as an effective control parameter to suppress the AFM phase and develop superconductivity.[8,23,37] Based on a number of experimental results, it is believed that antiferromagnetic spin fluctuation is the driving force for the development of the superconducting transition. In addition, valence instability is considered to be another key factor for the development of superconductivity in heavy-fermion compounds.[86] A famous example is the observation of pressure-induced reemergence of superconductivity in CeCu2Si2, whose pressure–TC phase diagram exhibits two superconducting domes,[8] as shown in Fig.
 | Fig. 7. (color online) Schematic phase diagram of Ce-based narrow-band metals. At low density, the Ce 4f orbitals are singly occupied and carry a static moment (arrows), subject to long-range antiferromagnetic order (red line). Increasing the lattice density (e.g., by hydrostatic pressure) raises the hybridization between more extended orbitals (single-hatched region) and the 4f states, leading to dynamical frustration (Kondo spin-flips; double arrows), which in turn suppresses long-range order and induces an anomalous normal state. In the simplest case, at some distance from the quantum critical point at Pc1, where magnetic order is fully suppressed, this state can be modeled as a high-effective-carrier-mass Fermi liquid. Sufficiently close to Pc1, magnetically mediated pairing may induce unconventional superconductivity (red dome). Further increasing the hybridization between localized and extended orbitals leads eventually to a less correlated, metallic state (intermediate valence region), in which the 4f electrons delocalize through stronger hybridization with ligand states and occupy wider energy bands at the Fermi energy (cross-hatched region). The transition from the heavy fermion to the intermediate valence configuration may proceed through a first-order phase transition that involves a collapse of the unit cell volume with no change in lattice symmetry (green dashed line), driven by the gain in cohesive energy associated with the wide-band 4f electron configuration. If the critical endpoint of the first-order line is low enough, the system may become sufficiently soft at low temperatures to allow a superconducting state to form around the quantum phase transition associated with the volume collapse, at Pc2 (green dome). Reproduced with permission from Ref. [8]. |
Recently, progress has been made in the pressurized non-centrosymmetric CeTX3 (where T = Co, Rh, or Ir and X = Si or Ge) family. Though ambient-pressure unit-cell volumes and critical pressures for superconductivity vary substantially across the series, all family members reach a maximum superconducting transition temperature 

High-entropy alloys (HEAs) are a new class of materials that are made from multiple transition-metal elements in equimolar or near-equimolar ratios.[89,90] The elements in HEAs arrange themselves randomly on the crystallographic positions of a simple lattice.[91–94] In many respects, HEAs exhibit excellent properties, including excellent specific strength,[95] ultrahigh fracture toughness at cryogenic temperatures,[96,97] and superior mechanical performance at high temperatures,[98] implying that HEAs have great potential for application. Significantly, superconductivity has been found in HEAs, making them more attractive in the field of materials science.[99,100]
Intriguingly, one of the HEA superconductors, (TaNb)0.67(HfZrTi)0.33, displays extraordinarily robust zero-resistance superconductivity under pressure as high as 190 GPa, a pressure that falls within that of the outer core of the earth [101], as shown in Fig.
 | Fig. 8. (color online) Phase diagram of superconducting transition temperature versus applied pressure up to 190.6 GPa for the HEAs, combined with plots of the corresponding resistance vs. temperature. Blue triangles and dark-yellow balls in the diagram represent the zero-resistance superconducting transition temperature TC obtained from measurements at pressure <60 GPa, while the red and green balls stand for zero-resistance TC from the measurements at pressures up to 179.2 and 190.6 GPa, respectively. Reproduced with permission from Ref. [101]. |
Superconductivity was first discovered in element Hg by Onnes,[102] initiating the research field of superconductivity. Later on, numerous element superconductors were discovered. Up to now, thirty three elements are found to be superconducting at ambient pressure.[103,104] By application of pressure, twenty four non-superconducting elements become superconductors,[105,106] as described in the periodic table (Table
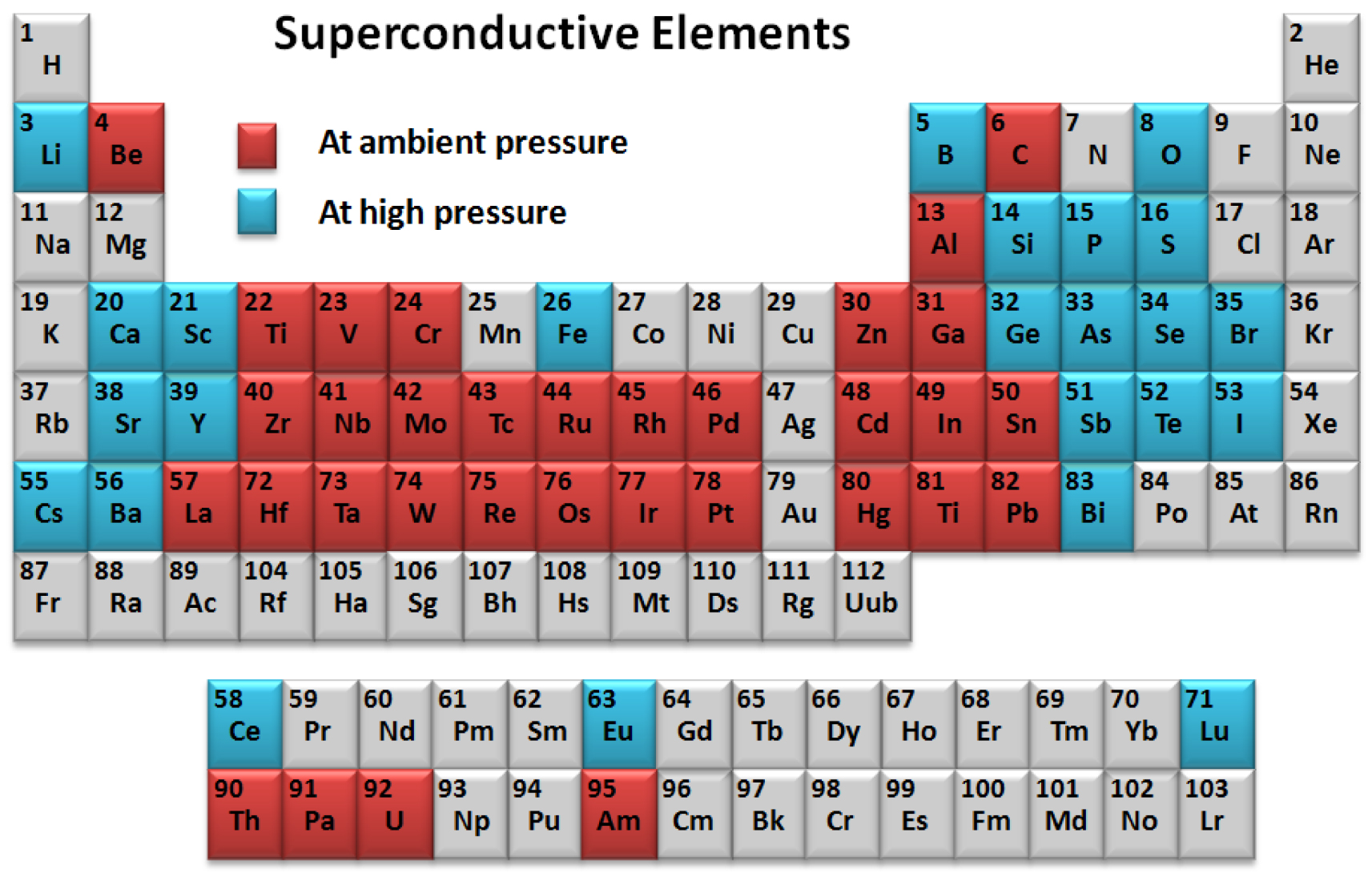 | Table 1. Periodic table displaying element superconductors at ambient pressure (highlighted in red) and superconductors (highlighted in blue) at high pressure. |
Remarkably, pressure can also enhance the superconducting transition temperature for the ambient-pressure element superconductors. Examples can be found in compressed zirconium (with its TC increasing from 0.55 K at ambient pressure to ∼ 11 K at 30 GPa[107]) and vanadium (with its TC increasing linearly with pressure and reaching ∼ 17 K at 120 GPa[108]). The highest TC value (29 K) in elements is found in pressurized calcium, as shown in Fig.
 | Fig. 9. (color online) Pressure dependence of TC for element Ca. The data are taken from Refs. [109] and [110] |
Because elements have a pure phase, they are ideal candidates to investigate fundamental physics. Recently, progress has been made in single-crystal black phosphorus.[111,112] Complementary measurements of high-pressure resistance, the Hall effect, and the crystal structure on black phosphorus reveal that hole carriers play an important role in developing superconductivity and enhancing TC in a single cubic superconductivity in a rhombohedral superconducting phase,[113] as shown in Fig.
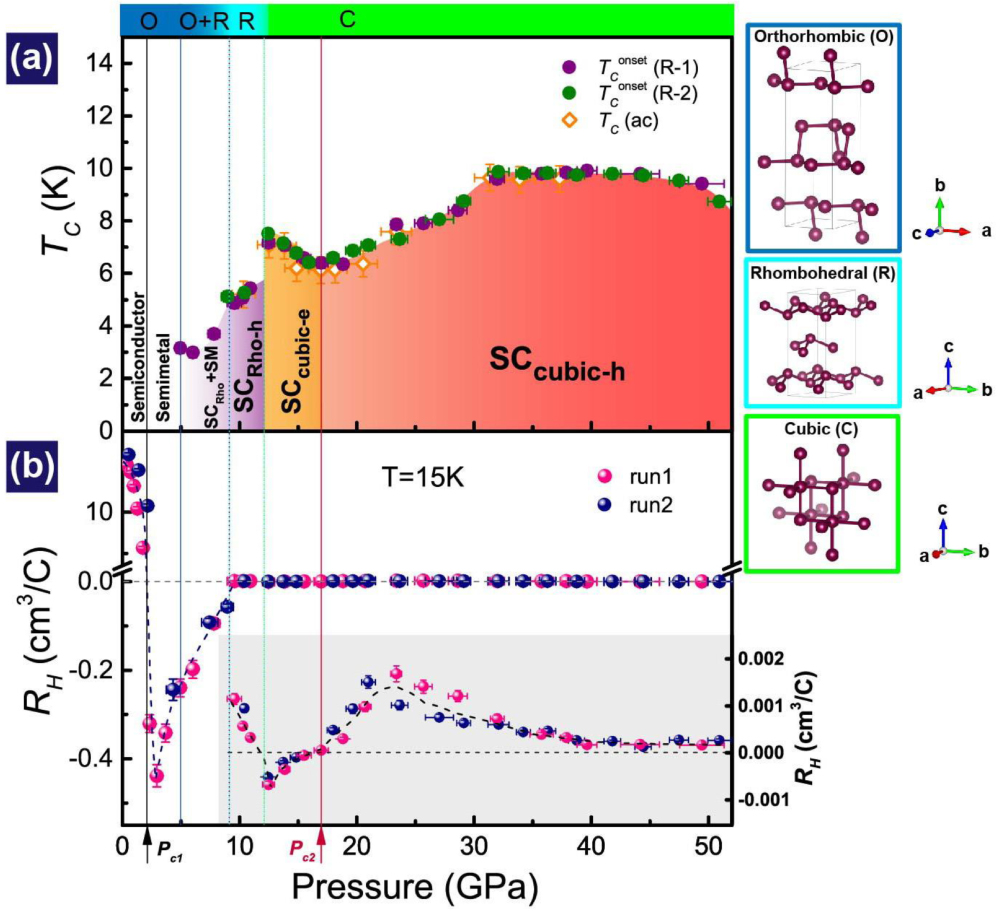 | Fig. 10. (color online) Structural, superconducting, and Hall coefficient (RH) phase diagram of black phosphorus at different pressures. (a) Pressure–temperature phase diagram combined with structural phase information. Here SM and SCRho-h represent semimetal and superconducting phases with rhombohedral structures and dominant hole carriers, respectively. SCcubic-e and SCcubic-h stand for the superconducting phase with cubic structure and dominance of electron carriers and hole carriers, respectively.
  |
Some impressive progress in the field of superconductivity research has been achieved through high-pressure studies in the past decades, including pressure-induced enhancement of superconducting transition temperatures in cuprates and FeAs-based superconductors, pressure-induced superconductivity in H2S, and the discovery of Fe-based and element superconductors. Furthermore, many other interesting discoveries have also been made, such as pressure-induced reemergence of superconductivity in heavy-fermion and FeSe-based superconductors, a bi-critical point in an FeAs-based superconductor, and the robustness of superconductivity in a HEA superconductor.
The system being established at SECUF, which integrates the extreme conditions of high pressure, low temperature, and a magnetic field, can perform in situ high-pressure (up to 100 GPa) resistance, magnetoresistance, and Hall measurements under low temperature (down to 500 mK) and magnetic field (up to 14 T). With such a powerful high-pressure system, together with other SECUF equipment, it can be expected that an unprecedented opportunity, never available before, for users to find phenomena and physics in condensed matter will be provided. In particular, SECUF will be built at the same campus as the Beijing high-energy synchrotron radiation facilities, at which beamlines for high-pressure x-ray diffraction, absorption, and inelastic scattering measurements will be established. Therefore, it is expected that the complementary high-pressure studies of the ‘in-house’ instruments and on-line synchrotron facilities will offer the combined advantage in achieving breakthroughs in frontier research fields of condensed matter physics, materials science, and even chemistry, geophysics, and astrophysics.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] | |
| [39] | |
| [40] | |
| [41] | |
| [42] | |
| [43] | |
| [44] | |
| [45] | |
| [46] | |
| [47] | |
| [48] | |
| [49] | |
| [50] | |
| [51] | |
| [52] | |
| [53] | |
| [54] | |
| [55] | |
| [56] | |
| [57] | |
| [58] | |
| [59] | |
| [60] | |
| [61] | |
| [62] | |
| [63] | |
| [64] | |
| [65] | |
| [66] | |
| [67] | |
| [68] | |
| [69] | |
| [70] | |
| [71] | |
| [72] | |
| [73] | |
| [74] | |
| [75] | |
| [76] | |
| [77] | |
| [78] | |
| [79] | |
| [80] | |
| [81] | |
| [82] | |
| [83] | |
| [84] | |
| [85] | |
| [86] | |
| [87] | |
| [88] | |
| [89] | |
| [90] | |
| [91] | |
| [92] | |
| [93] | |
| [94] | |
| [95] | |
| [96] | |
| [97] | |
| [98] | |
| [99] | |
| [100] | |
| [101] | |
| [102] | |
| [103] | |
| [104] | |
| [105] | |
| [106] | |
| [107] | |
| [108] | |
| [109] | |
| [110] | |
| [111] | |
| [112] | |
| [113] |



