Nowadays, LED products have already come into our sights and played a very important role in our daily life for their large range of applications in general illumination, energy-efficient lighting and backlights for screens. But some problems remain to be solved. We need to know that it is nearly inevitable to stop the efficiency droop with the injection current increasing. After years of study, it has been known that the physical origin of efficiency droop could be the Auger recombination,^[1] electron leakage,^[2–4] low mobility of the hole,^[5,6] and poor hole injection,^[7] and the polarization caused by the lattice mismatch at the interface of InGaN quantum well (QW) and quantum barrier (QB) as well as the last quantum barrier (LQB) and electron blocking layer (EBL).^[4,7]

A lot of efforts have been made to suppress the efficiency droop and improve the optical property of the InGaN-based light-emitting diode (LED) in the past few years. A lot of LED structures have been tried to achieve a better effect from different aspects. Some research focused on the EBL, such as graded AlGaN EBL^[8] and AlInN EBL^[9] to reduce the polarization between the last quantum barrier and EBL which hinders the holes from entering into the active region. Guo et al.^[10] enhanced the performances of blue GaN-based light-emitting diodes with double EBLs. Chen et al.^[11] enhanced the performances of AlGaInP-based light-emitting diodes with Schottky current blocking layers. Then in this paper, we pay more attention to the barriers. We notice that in many kinds of structures the attention has been paid to the barriers in order to improve the LED property recently. Kuo et al.^[12] used multiple GaN–InGaN barriers to replace the original GaN barriers. Xiong et al.^[13] adopted multiple GaN–InGaN barriers and AlGaN step-like barriers, with the electron blocking layer removed. Cheng et al.^[14] proposed a graded barrier InGaN light-emitting diode, whose efficiency is improved by increasing the indium composition barriers. Yan et al.^[15] studied the dual-blue light-emitting diode with asymmetric AlGaN barrier. Pan et al.^[16] investigated the high optical power and low-efficiency droop LED by using compositionally step-graded InGaN barriers. Chung et al.^[17] adjusted the In compositions in wells and barriers. Yang and Zeng^[18] improved the hole distribution by reducing In compositions in GaN–InGaN barriers. The above-mentioned methods of changing barrier structures can enhance the performance by alleviating the quantum-confined Stark effect to some extent, but the mobility of the holes is still a huge factor for its greater effective mass, which influences the hole transportation and then the radiative recombination between electrons and holes.

In the present paper, in order to enhance the mobilities of the holes and give more restrictions to the electrons, we propose that the original GaN barrier is replaced by the GaN/InGaN/AlGaN/InGaN/GaN barrier through increasing the In composition in the first InGaN layer and reducing the In composition in the other InGaN layers to form a valley where there are a two-dimensional electron gas (2DEG) and two-dimensional hole gas (2DHG) which is able to improve the hole mobility directly and makes it easier to drive holes from p-GaN side to n-GaN side, finally making the carrier distribution better.

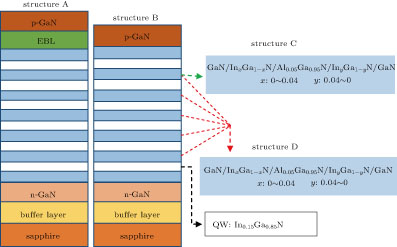
The structure of conventional InGaN-based LED (denoted as structure A) grown on a c-plane sapphire followed by a 2.5-μm thick GaN buffer layer, and a 0.5-μm thick layer of n-GaN:Si (5 × 10¹⁸ cm⁻³), is used as a reference in the study. There are six pairs of GaN/InGaN multiple quantum wells (MQWs) with 2-nm thick In_0.15Ga_0.85N wells and 11-nm thick GaN barriers in the active region. On the top of the MQW region is an 11-nm thick p-doped Al_0.15Ga_0.85N electron blocking layer (EBL): Mg (4 × 10¹⁷ cm⁻³) and 0.1-μm thick p-GaN:Mg (5 × 10¹⁷ cm⁻³). The second structure (denoted as structure B) has nothing different from structure A except the removal of the AlGaN EBL. In the third structure (denoted as structure C), the second-to-last GaN barrier is replaced by the GaN/InxGa_1−xN/Al_0.05Ga_0.95N/In_yGa_1−yN/GaN barrier on the basis of structure B. The thickness values of the special barrier are 1 nm, 4 nm, 1 nm, 4 nm, and 1 nm respectively to keep the thickness of GaN barrier unchanged. The x increases from 0 to 0.04 and y decreases from 0.04 to 0 gradually. In the last kind of structure (denoted as structure D), the middle five barriers are the special barriers that are used in structure B and no EBL either. Concrete structures and relevant parameters about the four structures are shown in Fig. 1.

Fig. 1.

	Figure Option ViewDownloadNew Window
	Fig. 1. (color online) Four kinds of LED structures.

The advanced physical model of semiconductor device simulation program (APSYS) is used to investigate the physical and optical properties of the four structures by solving the Poisson’s equation, the carrier transport equation, current continuity equations, the quantum mechanical wave equation and the photon rate equation. The area of the device geometry is 300 μm×300 μm. The Auger recombination coefficient and Shockley–Read–Hall (SRH) recombination time in quantum wells are set to be 1 × 10⁻³¹ cm⁶·s^−1[19] and 100 ns, respectively in the simulation. To simplify the simulation, the operating temperature is set to be 300 K. The background loss is assumed to be 2000 m⁻¹. The interface charge density is assumed to be 30% of the value calculated by the methods developed by Fiorentini^[20] considering the fixed defects and other interficial charge. The parameters left can be found in Ref. [21].

Figure 2 shows the energy band diagrams and quasi-Fermi levels of the four structures at a current density of 350 A·cm⁻². From Fig. 2(a), we can see that there is a severe downward slope from p-GaN side to n-GaN side for the conduction band between the LQB and the EBL in structure A, which can be attributed to the lattice mismatch between the last quantum barrier and the EBL, leading to a large polarization field at the LQB/EBL interface. The downward slope of the conduction band at the LQB will lower the effective potential height for electrons in the conduction band and make it easier for electrons to leak from the active region to the p-GaN side. On the contrary, the slope of the energy band will increase the effective potential height for holes in the valance band, resulting in a poorer hole injection and a worse efficiency droop. Now that the EBL has brought so many disadvantages, why should not we take another approach that could alleviate or eliminate the polarization effect at the interface of LQB/EBL and improve the injection efficiency of the carriers as well? So the second LED structure(structure B) is proposed in which there is no EBL on the top of LQB but a GaN/In_xGa_1−xN/Al_0.05Ga_0.95N/In_yGa_1−yN/GaN barrier used to replace the original GaN barrier is close to the LQB. Figure 2(b) shows that the energy band of structure B and the previous downward slope phenomenon disappear, but instead there appears an upward slope around the LQB after removing the EBL. The effective potential heights increase from 250 meV to 365 meV for electrons and decrease from 346 meV to 240 meV for holes, respectively, which will contribute to enhancing the number of the carriers within the active region. As can be seen in Figs. 2(c) and 2(d), valleys in the barrier are formed because of different energy band gaps of InGaN and AlGaN combined with the polarization at the InGaN/AlGaN interface caused by lattice mismatch in structure C and structure D.

Fig. 2.

	Figure Option ViewDownloadNew Window
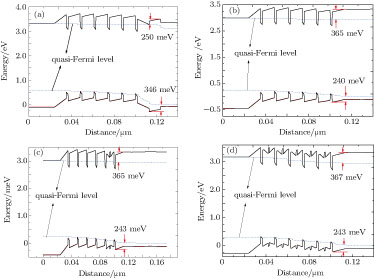	Fig. 2. (color online) Calculated energy band diagrams of structure A (a), structure B (b), structure C (c), and structure D (d) at a current density of 350 A·cm−2.

Figure 3 shows the concentrations of carriers (electrons and holes) at 350 A·cm⁻². For structure A, the densities of the electrons and holes vary widely in different QWs. The electrons mainly accumulate in the first and the last QWs .The carrier concentrations increase along the growing direction because of their mobilities (as noted before in this paper) for both structure A and structure B. But there is a little divergence in the last QW about the carrier concentration between the two structures, thus staying stable as a whole. When the special barrier is used in the structure C, the carrier concentration, especially the hole concentration increases greatly in the second-to-last well which is just before the special barrier comparing with that in the structure B. The carrier concentrations for the other four wells increase somewhat but not so evidently as those for the last two wells. What should be pointed out is that the hole concentration in the last well has a little reduction. As a result, the hole concentration in the two wells adjacent to the special barrier almost goes to an equivalent level and the electron concentration in the above two wells is closer than that in structure B. In total, the special barrier is able to modulate the distributions of holes and electrons in the two wells adjacent to the special barrier. This may be ascribed to the 2DEG and 2DHG around the valleys in the energy band as shown in Fig. 2(c).

Fig. 3.

	Figure Option ViewDownloadNew Window
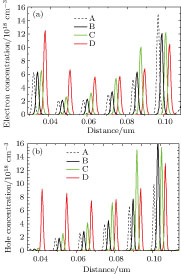	Fig. 3. (color online) Carrier concentration for electron (a) and hole (b) at a current density of 350 A·cm−2

Because of the spontaneous and piezoelectric-polarization around the InGaN/AlGaN interface, polarization-induced charge will be formed around the interface. Associated with a gradient of polarization in space is a polarization-induced charge density given by ρ p = −𝑝. Here we consider the polarization along the [0001] axis, since this is the direction along which epitaxial film and InGaN/AlGaN heterostructures are grown both in reality and our simulation. The spontaneous polarization along the c axis of the wurtzite crystal is 𝑃_SP = 𝑃_SPz. The piezoelectric polarization can be calculated with the piezoelectric coefficients e₃₃ and e₁₃ (listed in the following Table 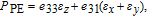1) as

(1)

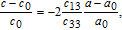(2)

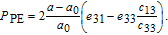(3)

Since [e₃₁ −e₃₃(c₁₃/c₃₃)] < 0 for AlGaN and InGaN over the whole range of compositions, the piezoelectric polarizations are negative for tensile and positive for compressive strained barriers, respectively. The spontaneous polarizations for GaN, AlN, and InN were found to be negative,^[27] meaning that the spontaneous polarization points towards the substrate. As a consequence, the alignments of the piezoelectrical and spontaneous polarization are parallel in the case of tensile strain, and antiparallel in the case of compressively strained top layers, respectively.

A polarization sheet charge density can be determined by

(4)

Here, we have a rough calculation on condition that the variation in none of composition, surface roughness, or strain distribution is taken into account to affect the distribution of polarization-induced sheet density. If the polarization-induced sheet charge density is positive (+σ), free electrons will tend to compensate for the polarization-induced charge. These electrons will form a 2DEG with a sheet carrier concentration, a negative sheet charge density (−σ) will cause an accumulation of holes, even a 2DHG at the interface.

Now we take InGaN/AlGaN (bottom/top) interface for example. To calculate the polarization-induced sheet charge density σ at the interface, we need to calculate the spontaneous and piezoelectric polarization in both the bulk material. First, for Al_xGa_1−xN, the spontaneous polarization and other parameters can be worked out by using the following set of liner interpolation between the physical quantities of GaN and AlN, i.e., piezoelectric polarization:

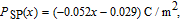(5)

lattice constant:

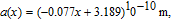(6)

elastic constants:

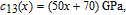(7)

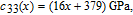(8)

piezoelectric constant:

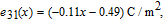(9)

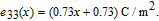(10)

Then we need to know the spontaneous and piezoelectric polarization of the bottom In_yGa_1−yN. By analogy, we can obtain the spontaneous polarization of the In_yGa_1−yN:

spontaneous polarization:

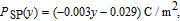(11)

From Eq. (3), for the GaN/InGaN (bottom/top) heterostructure, the piezoelectric polarization of In_yGa_1−yN is

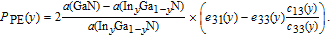(12)

The piezoelectric polarization of Al_xGa_1−xN can also be calculated in the same method. Then the polarization-induced sheet charge density σ at the InGaN/AlGaN interface is

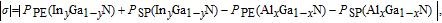(13)

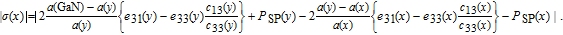(14)

When x = 0.04 and y = 0.05, the polarization-induced sheet charge density σ at the InGaN/AlGaN interface is 0.01548 C/m². The sheet charge σ/e is 0.967 × 10¹³ C/cm². Similarly, the polarization-induced sheet charge density σ at the AlGaN/InGaN interface is −0.01522 C/m². The sheet charge |σ/e| is 0.95 × 10¹³ C/cm². So we believe that the 2DEG and DHG can form in the InGaN/AlGaN and AlGaN/InGaN interface as shown in Fig. 4, which will improve the carrier mobility, especially for the holes. The hole with higher mobility makes it easier to be injected into the other wells, and this may be the reason why the hole concentration is distributed as what we can see in Fig. 3(b). As for the electron, more electrons will accumulate in the wells where the hole concentration is enhanced, the enhanced hole injection also helps to confine the electrons in wells. The carrier distribution of structure D indicates that the special barriers indeed bring what we expected, meaning that the special barriers are able to affect the distribution of carriers in the QWs.

Fig. 4.

	Figure Option ViewDownloadNew Window
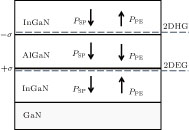	Fig. 4. Polarization-induced sheet charge density and direction of the spontaneous and piezoelectric polarization in InGaN/AlGaN and AlGaN/InGaN heterostructure.

Figure 5 shows the radiative recombination rate of all four structures at a current density of 300 A·cm⁻². The horizontal positions of these structures are shifted just by a small distance to make a better comparison. The radiative recombination rates rise along the growth direction in all wells for structures A and B. The radiative recombination rate for structure B achieves some improvement compared with that for structure A due to the removal of the EBL, thereby enhancing the hole injection efficiency. For the structure C, the radiative recombination in the fifth quantum well is pretty high because of the high concentrations for electrons and holes caused by the adoption of the GaN/InGaN/AlGaN/InGaN/GaN barrier in that barrier. But the radiative recombination rate in the last quantum well is lower than that in structure B, which is attributed to the reduction of hole number in the last quantum well. After the adoption of the special barriers in the middle five barriers, the radiative recombination rates in all six wells seem to be more uniform and much larger than those of structure A and B in the first five QWs. As for why the radiative recombination rate in the fifth well decreases, it is because the GaN/In_xGa_1−xN/Al_0.05Ga_0.95N/In_yGa_1−yN/GaN barrier that is able to modulate the carrier distribution in the adjacent wells just exits in front of the fifth well.

Fig. 5.

	Figure Option ViewDownloadNew Window
	Fig. 5. (color online) Radiative recombination of all structures.

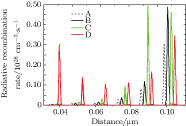
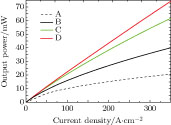
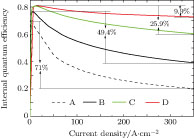
With the successful and effective modulation of the carrier distribution by the specially designed barriers, a great improvement in the light output power and IQE can be seen in Figs. 6 and 7. From Fig. 6, it is evident that the special barriers in the second-to-last barrier can enhance the performance of light output power and alleviate efficiency droop at a current density of 350 A·cm⁻². The light output power is 62 mW which is larger than 40 mW and 21 mW in structures A and B, respectively. The efficiency droop is 25.9% which is much smaller than 71% and 49.4% in structures A and B. What is more, when there are five specially designed barriers in the middle five QBs, a further improvement is achieved in structure D, with the light output power and the efficiency droop being 74 mW and 9.9%, respectively.

Fig. 6.

	Figure Option ViewDownloadNew Window
	Fig. 6. (color online) Light output power of all structures.

Fig. 7.

	Figure Option ViewDownloadNew Window
	Fig. 7. (color online) Plots of theoretical IQE versus injection current for the four structures.

The effects of special barriers are studied numerically in this paper. Simulation results indicate that the LED with one designed GaN/In_xGa_1−xN/Al_0.05Ga_0.95N/In_yGa_1−yN/GaN barrier replacing the original GaN barrier is able to enhance the hole injections for the first five wells, especially for the adjacent wells, but release the holes in the last QW close to p-GaN side and improve the electron concentrations in the second-to-last QWs remarkably at the same time, meaning that the special barrier is quite useful to modulate the carrier concentrations in the two QWs adjacent to that barrier to a relatively close level. Additionally, with the adoption of the special barriers in all of the middle five QBs, a higher concentration and better uniformity of the carrier contribute to the higher radiative recombination rate, light output power, and lower efficiency droop.