Cite this Article
Xu Xiulan, Zhang Yanhui, Cai Xiangji, Zhao Guopeng, Kang Lisha. Fractal dynamics in the ionization of helium Rydberg atoms. Chinese Physics B, 2016, 25(11): 110301  
Permissions
Fractal dynamics in the ionization of helium Rydberg atoms
Xu Xiulan1, Zhang Yanhui1, †, , Cai Xiangji2, Zhao Guopeng1, Kang Lisha1
College of Physics and Electronics, Shandong Normal University, Jinan 250014, China
School of Physics, Shandong University, Jinan 250100, China

 

† Corresponding author. E-mail: yhzhang@sdnu.edu.cn

Project supported by the Natural Science Foundation of Shandong Province, China (Grant No. ZR2014AM030).

Abstract
Abstract

We study the ionization of helium Rydberg atoms in an electric field above the classical ionization threshold within the semiclassical theory. By introducing a fractal approach to describe the chaotic dynamical behavior of the ionization, we identify the fractal self-similarity structure of the escape time versus the distribution of the initial launch angles of electrons, and find that the self-similarity region shifts toward larger initial launch angles with a decrease in the scaled energy. We connect the fractal structure of the escape time plot to the escape dynamics of ionized electrons. Of particular note is that the fractal dimensions are sensitively controlled by the scaled energy and magnetic field, and exhibit excellent agreement with the chaotic extent of the ionization systems for both helium and hydrogen Rydberg atoms. It is shown that, besides the electric and magnetic fields, core scattering is a primary factor in the fractal dynamics.

PACS: 03.65.Sq;34.50.Fa;05.45.Pq
Keyword:self-similarity structure;ionization dynamics;fractal dimension;helium Rydberg atom
1. Introduction

Over the past two decades, with the advancement of laser technology and semiclassical theory,[1–6] considerable attention has been paid to the ionization dynamics of Rydberg atoms and their photoionization or photodetachment in external fields.[7–13] The photoionization process in an electric field has been measured using a position-sensitive detector, which introduces the capability of visualizing an electric wave function on a macroscopic scale.[14–17] The chaotic ionization of hydrogen in parallel electric and magnetic fields is described by the Poincaré map.[18–21] The ionizing trajectories exhibit fractal self-similarity structures in the chaotic ionization of Rydberg atoms.[12] Recently, with the advancement of fractal physics, consideration has been given to fractal dynamics in quantum transport.[22] The escape dynamics of trapped ultracold atoms and Bose–Einstein condensates both exhibit fractal features.[23] Most investigations using a semiclassical description of Rydberg atoms in external fields have focused on hydrogen and alkali-metal atoms.[6,24–27] However, it is notable that, for helium Rydberg atoms with two atomic nuclei and other hydrogen-like atoms with only one electron in their outermost shell, the fractal dynamics in the presence of external fields remain unrealized. Hence, it is a challenge to find the correspondence between the fractal distribution in ionization systems and the escape dynamics of electrons in external fields.

In this paper, we use the semiclassical theory to investigate the self-similarity structure of helium Rydberg atoms in an electric field and introduce a fractal approach to describe the chaotic dynamical behavior. Moreover, the influences of the scaled energy and scaled magnetic field on the ionization mechanism are analyzed quantitatively. Comparing the fractal structures of helium atoms with those of hydrogen, we find that the escape time plots corresponding to different fractal dimensions show excellent agreement with the behavior of ionized electrons. Our research offers an efficient approach to describe the fractal dynamics in the ionization of Rydberg atoms. We hope that our results will provide a reliable theoretical basis for chaotic quantum transport and guide future photoionization microscopy experiments on helium or more complex atoms.

This paper is organized as follows. In Section 2, we briefly describe the ionization mechanism of helium Rydberg atoms and introduce the fractal method. The numerical results are discussed in Section 3, where we analyze the fractal structure of the escape time plot for helium atoms. Moreover, we calculate the corresponding fractal dimensions of both helium and hydrogen atoms under various external factors. The last section states the conclusions of our research.

2. Theoretical framework

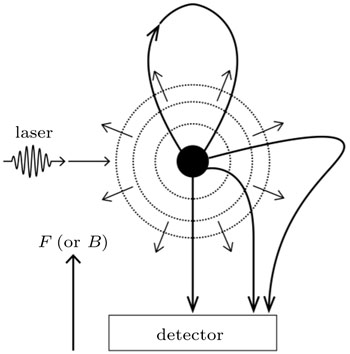
A schematic view of the ionization system is given in Fig. 1. We consider helium Rydberg atoms with only one excited electron placed in an electric field directed along the z axis. According to the closed orbit theory,[5,6] the outgoing wave packet that propagates away from the atomic core can be described as an ensemble of classical trajectories. When a laser pulse strikes the atom, the excited electron moves outward from the nucleus with an initial launch angle following classical trajectories, producing a spherical wave packet and being turned around by the applied field. Eventually the escaping electrons strike the detector.

Fig. 1. Schematic view of the ionization of Rydberg atoms. The atom is placed in an electric field F (or magnetic field B) that is oriented along the z axis and perpendicular to the detector plane. If the ionized electron absorbs a photon, the waves propagate outward in all directions, and the electron escapes from the atom along direct or indirect trajectories to the detector.

The Hamiltonian of highly excited electrons in helium atoms within an electric field can be written in cylindrical coordinates (ρ,z) as (in atomic units e = ħ = m = 1)

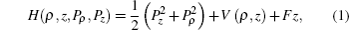
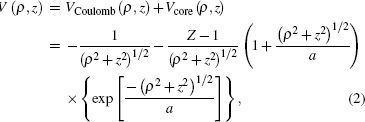
where the z-component of angular momentum is taken to be zero, F is the electric field strength, and V(ρ,z) is the Hüpper model potential, which can be written in the form[10,28]

where a is the parameter of the model potential determined by the range of the ion core, which is chosen to give the measured quantum defects,[29] and Z is the nuclear charge. For the helium Rydberg atom, Z = 2 and a = 1/3.[30]

In the following, by introducing the scaling law r̃ = rF1/2, P̃ = PF−1/4, ɛ = EF−1/2, t̃ = tF3/4,[31] we obtain the transformed Hamiltonian

To eliminate the Coulomb singularity, we adopt semi-parabolic coordinates (u,v) and their conjugate momenta (pu, pv), which are defined as[32,33]

where t̃ is the new scaled time variable. By introducing an effective form h = 2r̃(H̃ − ɛ), the final regularized Hamiltonian is given by

When h(u,v,pu,pv) = 0, we find that the regularized Hamiltonian generates the same mechanism as H̃ = ɛ.

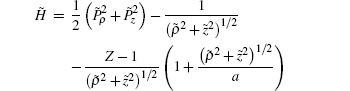
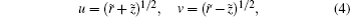
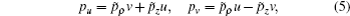
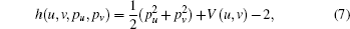
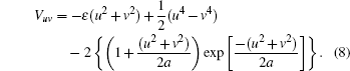
The above transformations remove the Coulomb singularity, and so every trajectory of the electron can launch from the origin and the Hamiltonian only depends on the scaled energy ɛ, rather than the energy E and the parameter F.

To investigate the chaotic escape quantitatively within the framework of the box-counting method[34] for the ionization of Rydberg atoms in external fields, the fractal dimension of the self-similarity structure that reflects the chaotic properties is defined as

The initial launch angles of the ionized electrons are equally divided into R parts, with those occupied by the chaotic regions marked as N(R). We quantify the chaotic dynamical behavior of the ionized electrons by giving the fractal dimension of the escape time as a function of the launch angle θ.

3. Results and discussion
3.1. Self-similarity structure

A contour plot of the potential Vuv (ɛ = −1.3) is shown in Fig. 2. The electron begins at the atomic nucleus (u = v = 0) and oscillates in the potential well under the combined influences of the core scattering and electric field. Finally, it passes over the saddle point and forms an ionizing trajectory, which is described by the thick line in Fig. 2.

Fig. 2. Contour plot of potential energy (ɛ = −1.3) with one ionizing trajectory.

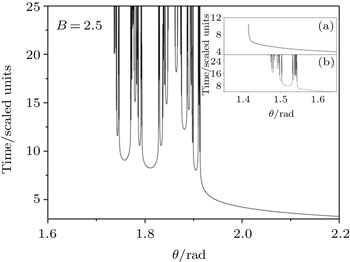
On account of the core scattering effect, multiple electrons can arrive at the detector plane and the escape behavior exhibits chaotic features. For the Hamiltonian in Eq. (7), based on the canonical equations of the Hamiltonian system we can perform iterative calculations. At the scaled energy ɛ = −1.3, we can identify the fractal self-similarity structure of the escape time plot of helium Rydberg atoms in an electric field.

The escape time curves are shown in Fig. 3, which is called an “icicle map”.[19–21] This figure demonstrates the relationship between the initial launch angles and the escape times of the ionized electrons. Three successive magnifications of the escape time plot are given by magnifying intervals of the distribution of initial launch angles. Such rules of self-similarity occur at many scales, and this demonstrates the scale-free features of the ionization system of helium Rydberg atoms.

Fig. 3. Successive magnifications of the escape time plot. (a) The time it takes the ionized electron to strike the detector is plotted as a function of the initial launch angle with scaled energy ɛ = −1.3, F = 19 V/cm. Every point on the graph represents one escape trajectory. (b) Magnification of assigned angle interval between 1.4865 and 1.51737 in panel (a). (c) Magnification of assigned angle interval between 1.4946 and 1.50175 in panel (b).

Figure 4 shows the escape time plots of Rydberg helium atoms at different scaled energies −1.5 ≤ ɛ ≤ −1.3. The self-similarity structure can be seen to occur at different initial launch angle ranges. These results indicate that the self-similarity region shifts toward larger initial launch angles. Most of the electrons with large outgoing angles reach the detector when the scaled energy is relatively small. Moreover, the complexity of the regions enclosed by dashed lines in Fig. 4 increases with the increasing scaled energy, which suggests that the chaotic characteristics are also being enhanced. This is because the chaotic escape behavior of the ionized electrons is controlled by the scaled energy. The probability of the electrons being ionized decreases when the scaled energy decreases, whereas the time the electron takes to strike the detector increases. In addition, electrons with large initial launch angles strike the detector relatively easily, so the width of the self-similarity region becomes gradually narrower and shifts toward larger initial launch angles. Both the location and range of the self-similarity exhibit a certain regularity, which demonstrates that the ionization of Rydberg atoms satisfies the basic rule of chaotic systems. By studying the structure of the escape time plot, we find that the chaotic extent of the ionization process is sensitive to the scaled energy. This is consistent with the Hamiltonian in Eq. (7) depending only on ɛ.

Fig. 4. Escape time plots for different scaled energies: (a) ɛ = −1.3, (b) ɛ = −1.4, (c) ɛ = −1.5.
3.2. Fractal dimension and chaotic escape

We now extract the fractal dimension to describe the chaotic extent of the ionization of helium Rydberg atoms in a quantitative manner.

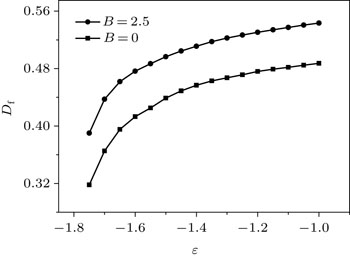
First, we plot a curve of the fractal dimension versus the scaled energy for B = 0 (see Fig. 5). This figure shows that, for helium Rydberg atoms placed in an electric field, the fractal dimension increases with the scaled energy above the ionization threshold. The core scattering plays an important role besides the Coulomb scattering, and the core-scattered trajectories propagate away from the nucleus in all directions and are turned around by the electric field. Thus, the behavior of the escaping electrons exhibits chaotic properties.

Fig. 5. Fractal dimension as a function of scaled energy for helium Rydberg atoms. The squares and circles indicate the fractal dimensions with scaled magnetic fields of B = 0 and B = 2.5, respectively.

The analytical method and fundamental theory above can be extended to ionization in parallel fields. By the analogous scaling laws[13,14] for helium Rydberg atoms in parallel electric and magnetic fields, the regularized Hamiltonian of the electron can be expressed as

where B is the scaled magnetic field strength. The fractal dimension versus the scaled energy for B = 2.5 is also illustrated in Fig. 5. As the strength of the magnetic field increases, the fractal dimension becomes higher than in a pure electric field (i.e., when B = 0). The ionized electron escapes from the atom, producing a spherical outgoing wave packet described by an ensemble of trajectories that encircle the nucleus several times under the influence of the Coulomb force and the applied external fields, as in Fig. 2. The system exhibits enhanced chaotic properties compared with the case of a pure electric field. We find that, besides the core scattering, the magnetic field is an important factor in the chaotic behavior of ionized electrons.

Considering the core scattering effect in the chaotic escape of electrons for helium atoms, we compared the ionization of hydrogen Rydberg atoms in pure electric and parallel fields at the scaled energy ɛ = −1.3. When the hydrogen atom is placed in an electric field (B = 0), the Hamiltonian of the electron is integrable. The escape time plot, shown in inset (a) of Fig. 6, follows a power-law distribution without the core scattering. This is different from the behavior of the helium atom, which is depicted in inset (b) of Fig. 6. The above analysis indicates that the core scattering effect leads to the chaotic escape of electrons from the helium atom. However, much more complex structures arise when the magnetic field (B = 2.5) is applied to the system. Hence, the influence of the magnetic field on the electron is a primary factor in the chaotic dynamics of the ionization process of hydrogen atoms.

Fig. 6. For hydrogen atoms in parallel electric and magnetic fields, the escape time required for electrons to strike the detector is plotted as a function of the initial launch angle with scaled energy ɛ = −1.3 and scaled magnetic field B = 2.5. Insets (a) and (b) represent hydrogen and helium atoms in a pure electric field (B = 0) with scaled energy ɛ = −1.3.

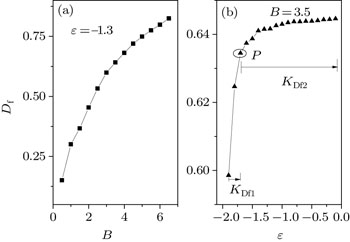
To further explore the influence of the magnetic field on the electrons, the relationship between the fractal dimension and scaled magnetic field is illustrated in Fig. 7(a). The fractal dimension increases with the scaled magnetic field, and the curve exhibits a roughly linear trend. The influences of electric, magnetic, and Coulomb forces cause the trajectory of the electron to circle the nucleus several times, and the escape behavior becomes accordingly complicated before the electron hits the detector. That is, the chaotic phenomenon of the system becomes increasingly apparent. Thus, we can adjust the strength of the magnetic field to control the escape behavior of the ionized electrons. This provides a theoretical basis to develop technology for manipulating the atom and the escape dynamics in external fields.

Fig. 7. (a) For hydrogen Rydberg atoms in parallel electric and magnetic fields, the fractal dimension as a function of the scaled magnetic field at fixed scaled energy ɛ = −1.3. (b) Fractal dimension as a function of the scaled energy under a fixed scaled magnetic field B = 3.5.

To investigate the influence of the scaled energy on the electrons, we calculated the fractal dimensions for different scaled energies under a fixed scaled magnetic field of B = 3.5. As shown in Fig. 7(b), the electron cyclotron effect plays a minor role when the scaled energy is relatively small near the ionization threshold, and this means the electrons cannot return back but are ionized directly. Thus, the fractal dimension is highly sensitive to the scaled energy. A fitting calculation shows that the slope of the curve is KDf1 = 0.1797 when the scaled energy −1.9 ≤ ɛ ≤ −1.7, but this drops rapidly to KDf2 = 0.0121 after the turning point P. The reasons are that some trajectories head downhill directly (direct trajectories), whereas other trajectories turn around the nucleus (indirect trajectories). The latter have longer escape times than the direct trajectories under the combined influence of electric, magnetic, and Coulomb forces. The interference between the outgoing and incoming waves produces a modulation in the distribution of direct and indirect trajectories. Compared with the case of helium atoms, we find that the tendency of the curve depicted in Fig. 5 for B = 0 is slowly increasing and the curvature is smaller than that of hydrogen, which fully demonstrates the effect of core scattering on the chaotic escape of ionized electrons. We can infer that the magnetic field induces chaos for the hydrogen Rydberg atoms, whereas for helium atoms, the core scattering must be taken into consideration.

4. Conclusions

We have studied the fractal dynamics of helium Rydberg atoms in an electric field within the framework of closed orbit theory. First, we found that a self-similarity structure exists in the escape time plot, and analyzed its chaotic properties qualitatively. The self-similarity region of the system was found to shift toward larger initial launch angles as the scaled energy decreases, which controls the fractal structure of the system. Moreover, core scattering induces the chaotic behavior of the ionization system. Second, we quantitatively analyzed the chaotic dynamical behavior of helium atoms, and obtained the fractal dimensions by analyzing the escape time plots. Finally, in a comparative analysis of hydrogen Rydberg atoms, we found that the fractal dimensions as a function of the scaled energy and scaled magnetic fields agree well with the chaotic escape dynamics in the ionization process. In addition, the influence of the magnetic field on the electrons is a primary factor in the chaotic extent of the hydrogen system. We believe that our work will provide a convenient tool for the fractal analysis of Rydberg atoms in external fields, and will be helpful to photoionization microscopy experiments for Rydberg atoms.

Reference
1Lackner FBřezinová IBurgdörfer JLibisch F 2013 Phys. Rev. 88 022916
2Yang B CDelos J BDu M L 2014 Phys. Rev. 89 013417
3Engl TDujardin JArgüelles ASchlagheck PRichter KUrbina J D 2014 Phys. Rev. Lett. 112 140403
4Zhao G PZhang Y HCai X JXu X LKang L S 2016 Physica 84 10
5Du M L 1989 Phys. Rev. 40 4983
6Du M LDelos J B 1988 Phys. Rev. 38 1896
7Yang G CMao J MDu M L 1999 Phys. Rev. 59 2053
8Zhao L BDelos J B 2010 Phys. Rev. 81 053417
9Zhao L BDelos J B 2010 Phys. Rev. 81 053418
10Hüpper BMain JWunner G 1996 Phys. Rev. 53 744
11Lankhuijzen G MNoordam L D 1996 Phys. Rev. Lett. 76 1784
12Zhou HLi H YGao SZhang Y HJia Z MLin S L 2008 Chin. Phys. 17 4428
13Wang D H 2011 Chin. Phys. 20 013403
14Blondel CDelsart CDulieu F 1996 Phys. Rev. Lett. 77 3755
15Nicole COfferhaus H LVrakking M J JLépine FBordas C 2002 Phys. Rev. Lett. 88 133001
16Lépine FBordas CNicole CVrakking M J J 2004 Phys. Rev. 70 033417
17Nicole CSluimer IRosca-Pruna FWarntjes MVrakking MBordas CTexier FRobicheaux F 2000 Phys. Rev. Lett. 85 4024
18Mitchell K AHandley J PTighe BFlower ADelos J B 2004 Phys. Rev. 70 043407
19Mitchell K AHandley J PTighe BFlower ADelos J B 2004 Phys. Rev. Lett. 92 073001
20Mitchell K AHandley J PTighe BDelos J BKnudson S K 2003 Chaos 13 880
21Mitchell K AHandley J PDelos J BKnudson S K 2003 Chaos 13 892
22Kotimäki VRäsänen EHening HHeller E J 2013 Phys. Rev. 88 022913
23Mitchell K ASteck D A 2007 Phys. Rev. 76 031403R
24Peters A DJaffé CDelos J B 1994 Phys. Rev. Lett. 73 2825
25Wang D HDing S LLin S L 2003 J. Phys. 36 4225
26Song X HLin S L2003Acta Phys. Sin.521611(in Chinese)
27Deng S HGao SLi Y PXu X YLin S L 2010 Chin. Phys. 19 040511
28Hüpper BMain JWunner G 1995 Phys. Rev. Lett. 74 2650
29Delande DTaylor K THalley M HVeldt T V DVassen WHogervorst W 1994 J. Phys. 27 2771
30Delande DBuchleitner A1995Adv. Atom. Mol. Opt. Phys.3485
31Raithel GHeld HMarmet LWalther H 1994 J. Phys. 27 2849
32Marcinek RDelande D 2000 Phys. Rev. 62 062704
33Delande D1991Phys. Scr.3452
34Ree SReichl L E 2002 Phys. Rev. 65 055205R