† Corresponding author. E-mail:
Project supported by the National Basic Research Program of China (Grant No. 2012CB619306), the Beijing Science and Technology Project, China (Grant No. Z151100003315024), and the National Natural Science Foundation of China (Grant No. 61404132).
The exciton–phonon interaction in Al0.4Ga0.6N/Al0.53Ga0.47N multiple quantum wells (MQWs) is studied by deep-ultraviolet time-integrated and time-resolved photoluminescence (PL). Up to four longitudinal-optical (LO) phonon replicas of exciton recombination are observed, indicating the strong coupling of excitons with LO phonons in the MQWs. Moreover, the exciton–phonon coupling strength in the MQWs is quantified by the Huang–Rhys factor, and it keeps almost constant in a temperature range from 10 K to 120 K. This result can be explained in terms of effects of fluctuations in the well thickness in the MQWs and the temperature on the exciton–phonon interaction.
AlGaN-based multiple quantum wells (MQWs) with high Al content have attracted intensive attention for their device applications in deep-ultraviolet (DUV) light emitting diodes (LEDs),[1–3] laser diodes (LDs),[4,5] and detectors.[6,7] Understanding light emission and absorption mechanisms in AlGaN MQWs is important for developing these devices. The exciton–phonon interaction, one of the intrinsic physical properties, is an important effect that appears in the optical process. The lattice vibration perturbs the motions of electrons/excitons in different ways, resulting in the various types of electron/exciton–phonon interactions, such as the Fröhlich interaction with longitudinal optical (LO) phonons, deformation–potential interactions with optical and acoustic phonons and piezoelectric interaction with acoustic phonons. The Fröhlich interaction is stronger than the other interactions due to the ionic nature of III–nitrides, which has a strong influence on the optical and transport properties of III–nitrides.[8,9]
Previous researches on exciton–phonon interactions in GaN epilayers,[10] AlN epilayers,[9] InGaN/GaN MQWs, and GaN/AlGaN MQWs[11] have been reported. The LO phonons in GaN and AlN epilayers have energies of about 92 meV[10,12] and 110 meV,[9] respectively. The exciton–phonon coupling strengths in various epitaxial structures, such as thin films, MQWs and quantum dots determine the optical transitions. As far as we know, the exciton–phonon interactions in the AlGaN/AlGaN MQWs have been less studied due to the lack of high quality materials. Additionally, the experimental results as reported on GaN-based quantum wells such as InGaN/GaN and GaN/AlGaN MQWs are controversial because of the complicated exciton–phonon interactions in these low dimensional GaN-based structures. Both reduced and enhanced exciton–phonon interactions in the nitride MQWs in comparison with those in nitride bulk materials have been reported.[10,11,13]
In this paper, deep-ultraviolet time-integrated and time-resolved photoluminescence (PL) measurements are performed on the Al0.4Ga0.6N/Al0.53Ga0.47N MQWs fabricated by using metal–organic chemical vapor deposition (MOCVD). Up to four LO-phonon replicas of exciton recombination are observed. The Huang–Rhys factor, which reflects the exciton–phonon coupling strength, is deduced from the ratio of the emission intensity of phonon replicas to that of the zero phonon line. The temperature insensitivity of the Huang–Rhys factor is explained in terms of the effects of fluctuations in the well thickness and the temperature on the exciton–phonon interaction in the MQWs.
The MQWs used in this study were grown on a c-plane sapphire substrate by metal organic chemical vapor deposition. Prior to the growth of AlGaN/AlGaN MQWs, an AlN buffer layer about 600 nm was grown on the sapphire substrate, which was followed by an Al0.62Ga0.38N epilayer with a thickness of about 600 nm. Then the AlGaN/AlGaN MQWs of 20 periods were deposited on the epilayer. The Al compositions in the AlGaN wells and AlGaN barriers were 0.4 and 0.53, respectively, while the thickness values of AlGaN wells and AlGaN barriers were 2.3 nm and 7.3 nm, respectively. The Al compositions and the thickness values of AlGaN wells and AlGaN barriers were determined by the measurement of XRD ω scans of (002) planes. Finally, an Al0.53Ga0.47N cap layer about 8 nm in thickness was covered on the MQWs.
The time-integrated and time-resolved PL measurements were performed by using our home-made deep ultraviolet laser spectroscopy system with a frequency-tripled fs Ti:sapphire laser as the excitation source, providing an excitation wavelength of about 237 nm. The diameter of the excitation area on the sample was about 100 μm, and the sample temperature was varied from 10 K to 180 K. Time-resolved PL spectra were recorded by a stand streak camera acquisition system, and the overall time resolution of the system is less than 16 ps. For the time-integrated PL, the spectral resolution was about 0.03 nm at 300 nm.
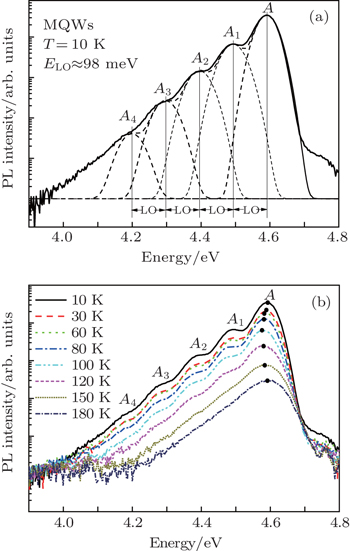
The time-integrated photoluminescence spectrum of Al0.4Ga0.6N/Al0.53Ga0.47N MQWs measured at T = 10 K is plotted in Fig.
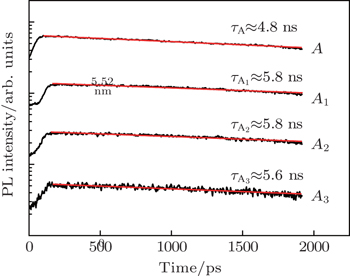
In order to investigate the recombination properties of the main emission peak and the phonon replicas in the PL spectrum of the Al0.4Ga0.6N/Al0.53Ga0.47N MQWs, the time-resolved PL measurements are performed. Figure
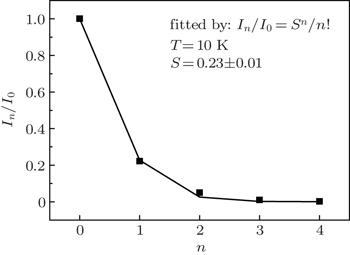
The distributions of the emission intensities among the main peak (n = 0) and the phonon replicas (n = 1, 2, 3, 4) depend strongly on the exciton–phonon coupling strength.[22,23] This coupling is expressed by the Huang–Rhys factor S within the Frank–Condon approximation. At low temperature, the relationship between the intensity of the n-th phonon replica In and the intensity of the main emission I0 is given by[8]
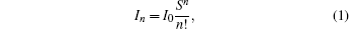
Figure
The Huang–Rhys factor in the Al0.4Ga0.6N/Al0.53Ga0.47N MQWs is extracted by fitting the observed relative intensities In/I0 to Eq. (
In this work, the exciton–phonon interaction in the Al0.4Ga0.6N/Al0.53Ga0.47N MQWs is investigated by deep-ultraviolet time-integrated and time-resolved PL. LO phonon replicas of exciton recombination with up to four phonons in the PL spectra are experimentally observed, indicating the strong coupling of excitons with LO phonons in our sample. Measuring the lifetimes of LO phonon replicas may be preferable to determine the PL recombination lifetime of the MQWs. In addition, it is found that the exciton–phonon coupling strength S is nearly invariable in the temperature range from 10 K to 120 K, which may be due to the fact that the balance between a thermally enhanced phonon assisted transition probability with temperature resulting in the increase of S factor and a thermally activated transfer of excitons from the thick region to the relatively thin region in wells leads to the reduction of S factor.
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 | |
| 18 | |
| 19 | |
| 20 | |
| 21 | |
| 22 | |
| 23 | |
| 24 | |
| 25 | |
| 26 | |
| 27 | |
| 28 |