† Corresponding author. E-mail:
Project supported by the National Science and Technology Major Project of China (Grant No. AHJ2011Z001) and the Major Research Project of Yili Normal University (Grant No. 2016YSZD05).
Non-line-of-sight imaging detection is to detect hidden objects by indirect light and intermediary surface (diffuser). It has very important significance in indirect access to an object or dangerous object detection, such as medical treatment and rescue. An approach to locating the positions of hidden objects is proposed based on time delay estimation. The time delays between the received signals and the source signal can be obtained by correlation analysis, and then the positions of hidden objects will be located. Compared with earlier systems and methods, the proposed approach has some modifications and provides significant improvements, such as quick data acquisition, simple system structure and low cost, and can locate the positions of hidden objects as well: this technology lays a good foundation for developing a practical system that can be used in real applications.
The non-line-of-sight imaging is the way to detect hidden objects, which cannot be reached directly by human vision, such as around a corner or behind a diffuser, and it has received much attention in recent years. For the imaging around the corner the reflection and diffusion of light are mainly used. It needs to rely on an intermediate medium which has the property of reflection or diffusion. For the imaging that relies on the diffuse intermediate medium, the laser source is focused onto a diffuser with characteristics of transmission and diffusion, the light scatters through the diffuser and spreads on a hidden object, then the light is scattered back again to the diffuser by the hidden object. It is finally obtained by the detectors which receive the backscattered light.
Earlier, the range-gated technology is used to obtain the non-line-of-sight imaging,[1,2] and it depends on the reflection of the intermediate medium (glass, metal frame and ceramic tile). The reflection imaging of the hidden object in the house can be detected by a range-gated camera. The light can also scatter through the opaque objects and imaging.[3] The “seeing around the corner” is the main way of non-line-of-sight imaging, and it usually uses the active imaging.[4] The hidden objects imaging behind a diffuser is another way, such as non-invasive imaging through opaque scattering layers.[5]
The technique of the time-of-flight (TOF) was used to investigate the inverse light transmission.[6] The method proved the existence of a set of inter-reflection cancelation operators that enable computing each n-bounce image. Femtosecond transient imaging utilized the ultrafast laser and picosecond streak camera to see the hidden objects around the corner.[7–11] They used the multiple reflections and five-dimensional (5D) time-light transmission matrixes; the reconstruction method was to make the elliptical tomographic projection. The three-dimensional (3D) hidden object around the corner has been reconstructed and the resolution achieved a precision of sub-millimeter depth. They continued to reconstruct the wide-angle, spatially varying reflectance hidden objects behind the ground glass diffuser, in which they used time-resolved inversion of backscattered light.[12,13] The different indirect and direct illumination concepts (point, surface and volume scattering sources) were also discussed to reconstruct hidden objects in non-line-of-sight imaging,[14] and they mainly focused on the large scales (on a meter scale) and a relatively long image acquisition time. Compared with the high resolution streak camera, the time-gated single photon avalanche diode (SPAD) for detecting the time-of-flight information has low cost with maintaining a comparable time resolution.[15] The SPAD was also used to track the hidden objects around corner.[16]
The reconstruction algorithm of non-line-of-sight imaging primarily depends on the information obtained by the detectors. The range-gated imaging technology[1,2] does not require reconstruction, the CCD camera captures the images reflected from the intermediate medium directly, but the image resolution is low. In the femtosecond transient imaging system used is the streak camera which obtains the streak images of hidden objects around the corner. The forward model of light transmission is established by elliptical tomographic projection and the filtered back projection is used in the reconstruction algorithm. The SPAD can detect the backscattered photons, and the time correlated single photon counting (TCSPC) module is used to produce a histogram of the photon counts versus the number of time bins after the illumination pulse. In the reconstruction method the back projection algorithm is also used. Currently, the conceptions of most proposed algorithms are of chromatographic process, which is similar to computer tomography (CT). So the general method is to perform the tomographic reconstruction, and the back projection algorithm is used to image reconstruction. The back projection algorithm is also used in synthetic aperture radar system.[17] The tomography reconstruction algorithms require data acquisition many times, the light source needs repeating on many spots, and the detectors also record data repetitively for multiple data acquisition correspond, so data collection needs to take a long time. Due to a large number of data acquisitions, the reconstruction is also slow. The detector requires high accuracy and sensitivity, which is expensive (such as picosecond streak camera). Those shortcomings block the practical applications.
In the paper, we present a different reconstruction algorithm based on time delay estimation for the localization of hidden objects. There is a certain time delay between different signals. When the signal arrives at the detector at different times, the location of the reflect signals are estimated by the time delay. The light source in our system only focuses on one spot and does not need to repeat many spots and times, neither does the data acquisition. Accordingly, the data acquisition is finished simultaneously. The structure of the system shows simpler and lower cost. The reconstruction algorithm based on the time delay estimation can locate the hidden object in real time.
The time delay estimation (TDE) algorithm is based on time difference of the arrived signals between the different detectors. The position and direction of the return signal can be located by the TDE algorithm. It is an important part of signal processing in signal detection, and is widely used in radar systems, sonar systems, communications and biomedical fields.[18–22] Estimation of the acoustic signal is the most widely used, according to the similar characteristics of acoustic field propagation and light field propagation, the localization method of the sound field can be applied to the light field.
The basic idea of TDE is that by measuring the time interval t of signal propagation, under the known speed of light v in air and the distance s can be obtained, and ultimately using s the location of source or reflector is determined.
For the active detection system, the source signal is s(n), the received signal is detected by the detector, and it can be described by the following mathematical expression:

Cross-correlation function is used in the basic method of estimating the time delay between the two signals,[23,24] the correlation function of source signal and the received signal is expressed as
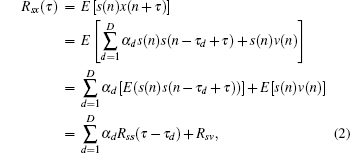

With the property of the auto-correlation function, when τ−τd = 0, Rss reaches a maximum value, and the correlation value between the two received signals is maximal, so choose τ as the delay value when the Rss (τ − τd) is maximum:

The laser pulse propagation process is shown in Fig.
A laser source is in the form of time domain signal, and can be expressed as[25]
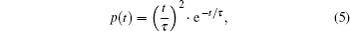
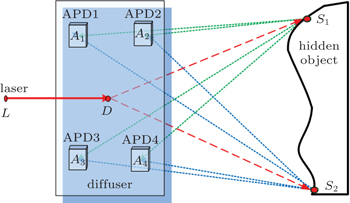
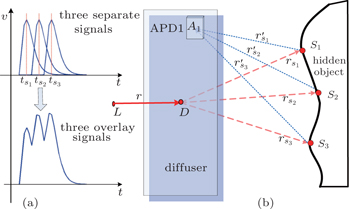
We consider the case of received signal by one APD, and select three points on the hidden object randomly (points S1, S2, and S3), and the light propagation process is shown in Fig. 
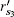
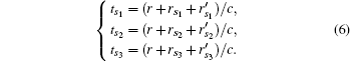
Since the distance between points of the hidden object is very small, the time delays among the return signals are small too and less than the laser pulse width generally, the received signals will be overlaid. Each APD detector should receive overlaid signals, which are shown in the lower part of Fig.
Figure

The basic method of estimating TDE is to calculate the correlation function between the source signal and the received signal, and estimate the time delay between them. According to the time delay information and the light propagation velocity, the position of the hidden object can be located.
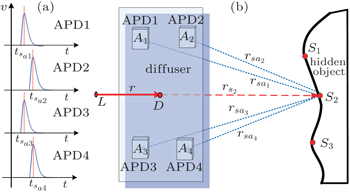
Let the received signals of four APDs be a1(t), a2(t), a3(t), and a4(t), the source signal is p(t), according to formula (
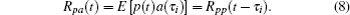
The correlation signal is calculated from formula (
The position of the object is assumed to be s2 (x,y,z) in Fig.
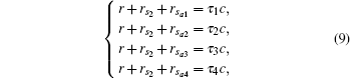
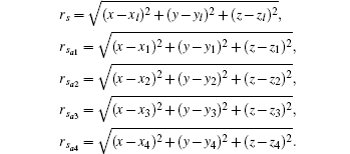

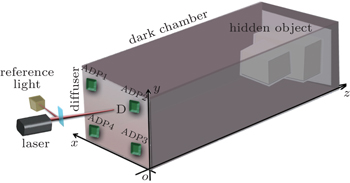
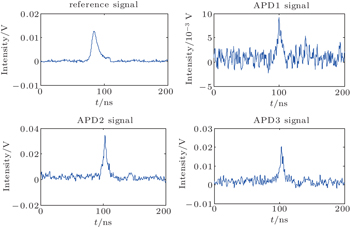
In the experiment, the laser source is a pulse-mode 1064 nm with 10-ns pulse width at a repetition rate of 10 kHz, and has an average power of 1W. The detectors are four APDs. Oscilloscope with a sampling rate of 1 GHz is used to data acquisition. Experimental setup of scene is shown in Fig.
The light source is focused onto the diffuser and scatters through the diffuser toward the hidden object, the light beams scatter back onto the diffuser and are received by APDs. Three APDs record the returned signals for each light incident on the diffuser. The light in the system is only focused on one spot and the data acquisition is finished simultaneously. We have carried out two experiments in the present work.
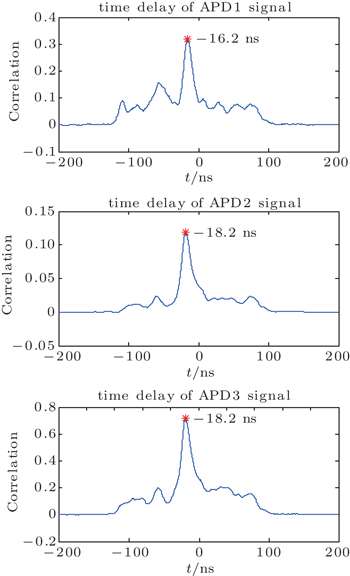
The time delay estimation between source signal and three APD signals are shown in Fig.
The three time delay values are −16.2 ns, –18.2 ns, and –18.2 ns of the correlation signals in Fig.
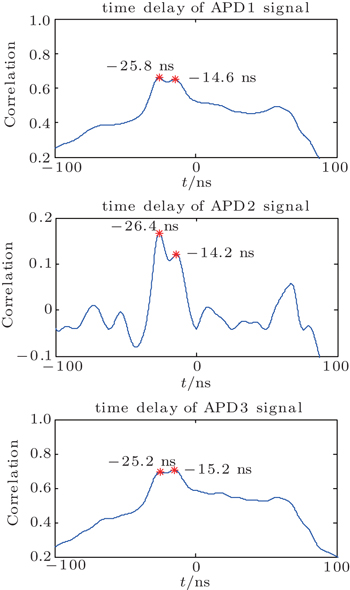
The results of time delay are shown in Fig.
We use a quasi-Newton iteration method to calculate the locations of hidden objects; the results are 413 cm and 241 cm. The depths of two hidden objects are 333 cm and 161 cm which subtracts the distance 80 cm from light point L to point D on the diffuser.
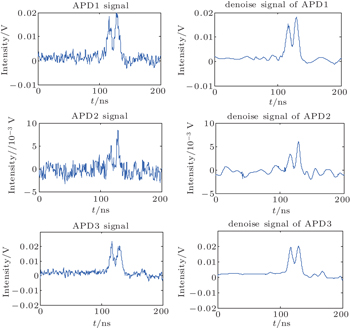
As shown in Figs.
In our experiment, the light source only focuses on single position, the detectors receive the signals from the hidden objects simultaneously, and the locating algorithm can also be finished in real time. The proposed method can achieve rapid and real-time location of the object position with simple structure. It is expected to be applied to the practical application.
We use a near-infrared laser source, which scatters through the diffuser and continues to spread onto the hidden objects, the light scatters back again from the hidden objects and reflects to the diffuser, finally the light beams are received by the detectors. The experimental data are obtained from the experiment setup with a darkroom in laboratory. The time delay estimation method is presented, we use the correlation algorithm to obtain the time delays between the received signals and the source signal. With the time delay and distance information, and using the quasi-Newton iteration method (Eq. (
The system proposed in the present paper can recognize hidden targets behind camouflage, vegetation, water, haze and fog, fire, and smoke. It can detect hidden objects which cannot be directly observed, and applied to medical treatment, rescue, and other potential object detection.
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 | |
| 18 | |
| 19 | |
| 20 | |
| 21 | |
| 22 | |
| 23 | |
| 24 | |
| 25 | |
| 26 | |
| 27 |