† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant No. 41276187), the Global Change Research Program of China (Grant No. 2015CB953901), the Priority Academic Development Program of Jiangsu Higher Education Institutions (PAPD), Program for the Innovation Research and Entrepreneurship Team in Jiangsu Province, China, the Canadian Program on Energy Research and Development, and the Canadian World Class Tanker Safety Service.
To study the electromagnetic backscattering from a one-dimensional drifting fractal sea surface, a fractal sea surface wave–current model is derived, based on the mechanism of wave–current interactions. The numerical results show the effect of the ocean current on the wave. Wave amplitude decreases, wavelength and kurtosis of wave height increase, spectrum intensity decreases and shifts towards lower frequencies when the current occurs parallel to the direction of the ocean wave. By comparison, wave amplitude increases, wavelength and kurtosis of wave height decrease, spectrum intensity increases and shifts towards higher frequencies if the current is in the opposite direction to the direction of ocean wave. The wave–current interaction effect of the ocean current is much stronger than that of the nonlinear wave–wave interaction. The kurtosis of the nonlinear fractal ocean surface is larger than that of linear fractal ocean surface. The effect of the current on skewness of the probability distribution function is negligible. Therefore, the ocean wave spectrum is notably changed by the surface current and the change should be detectable in the electromagnetic backscattering signal.
There are many types of ocean currents with different spatial and temporal scales on the ocean surface. They are essential components of the ocean circulation system and the relevant ecosystem. Ocean currents play important roles in the transportation of heat, mass, momentum, nutrients and energy.[1]
Remote sensing by satellite is the ideal technology for studying hydrodynamic dynamics of the ocean surface. It can obtain daily and weekly global coverage data with high revisit frequency and high spatial resolution by synthetic aperture radar (SAR). Chapron et al.,[2] and Johannessen et al.[3] derived an indirect retrieval algorithm for ocean surface current from the SAR Doppler frequency shift, as observed in the imagery. This method can only retrieve ocean current velocity in the range direction and the current direction is only derived with the aid of ancillary information. Marghany[4] improved the retrieval method for ocean current for RADARSAT-1 measurements by SAR imagery through using a method based on wavelength discrepancy and multiple looks at different frequencies. Some relevant studies and publications have reported ocean current retrieval results in different geographical areas by using TerraSAR-X, and Envisat ASAR.[5,6] Unfortunately, there is no method to directly measure ocean currents by sensors on satellites presently.
For ocean surface current, it is necessary to study the remote sensing mechanism, where the effect of the ocean current on electromagnetic (EM) backscattering of the sea surface is a key step to solve the problem. The surface current can modulate the EM backscattering signal because the current can change the wave parameters such as wave spectrum, wave height, wave period and other relevant variables. As a case study, the shoaling wave experiment (SHOWEX) shows that there is a drift of the wind wave spectrum with the mean wind direction because of horizontal current shear at the edge of the current front.[7] Therefore, there is an obvious correction of the amplitude dispersion relation, which is needed in the shallow water area.[8] Numerical results for the time evolution of the shallow water wave show that offshore currents can occur when a wave propagates and breaks in topographically changing shallow water, whereas the intensity and scale of the offshore current can be weakened by negative feedback because of the wave–current interaction.[9]
A fundamental objective of our study is to establish a high accuracy sea surface model. The fractal geometry method has characteristics of both periodicity and stochasticity. It can therefore be easily used to simulate the sea surface. Many recent studies focused on the fractal sea surface model and have used this approach to study EM scattering at the sea surface.[10–17] In this paper, the one-dimensional linear and nonlinear fractal sea surface models are used to derive wave–current coupled models, based on the wave–current interaction mechanism.
Nonlinear wave–current coupled models are derived in Section 2. An error analysis of our models is given in Section 3. Numerical simulation of the effect of the ocean current on the waves is given in Section 4. Conclusions are shown in Section 5.
Starting with linear and nonlinear fractal sea surface models, linear and nonlinear wave–current models are derived in this section.
For a one-dimensional linear irrotational flow system, the velocity potential function is





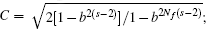
Assuming a linear sea surface and based on the basis of long-wave–short-wave interactions, Xie et al.[10] presented a model for the nonlinear fractal sea surface as follows:

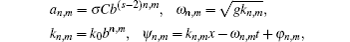

Ryu et al.[19] developed a numerical wave tank (NWT) with free surface boundary conditions to investigate wave–current interactions and the resulting kinematics. Inspired by their method, we derive a one-dimensional nonlinear wave–current fractal sea surface model in this paper.
A schematic diagram of the numerical wave tank (NWT) and its boundaries are shown in Fig.
Assuming that the surface current is uniform and C0 is in the x direction, the velocity potential of the sea surface current is


The wave should be completely dissipated in the artificial damping zone. According to the boundary conditions on the input boundary (L), the wall (R), and the bottom (B), we have















Considering nonlinear wave–wave interaction between the long wave and short wave, the nonlinear fractal sea surface model is derived as given in Eq. (



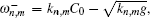
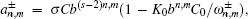
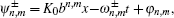
To estimate the accuracy of our wave–current couple model, wave amplitude is selected to numerically calculate relative error.
Longuet-Higgins and Stewart[18] suggested that the variation in energy of the short wave is caused by the work done by the long wave against the radiation stress of the short wave. According to the Longuet-Higgins and Stewart study, orbital velocities near the free surface have the horizontal component





The relative error er of the difference between the wave amplitude in deep water from our model and that from the analytic solution by Longuet-Higgins MS and Stewart,[18] is

Figure
Moreover, the limit of the possible numerical application of our model is studied here. According to Stokes wave theory, the maximum steepness of ocean wave is 0.142. Therefore we let wave steepness increase from 0 to 0.142, and let the velocities of sea surface currents range from −2 m·s−1 to 2 m·s−1. Therefore, the RMS relative wave amplitude error varies with wave steepness and velocity of sea surface current as shown in Fig.
 | Fig. 3. Variation of RMS relative wave amplitude error with wave steepness and sea surface current velocity. |
Numerical results show that our model can simulate 92% of the case shown in Fig.
To find the differences between the current effect on the nonlinear sea surface model and that on its wave–current coupled model, the initial conditions are set to be the same as previous ones, i.e., x = 1 m, λ0 = 200 m, b = 2e/3, σ= 075, s= 13, and N= 25. According to Eq. (
The effect of ocean surface current on wave amplitude is investigated here. Suppose that the velocity of the ocean surface current is positive when the current direction is the same as the wave propagation direction, and negative when the current direction is opposite to the wave propagation direction. Let C0 = ±0.5 m·s−1 and C0 = 0 m·s−1; the effects of current on the wave amplitude for different cases are shown in Fig.
The effects of current on wave amplitude are shown in Fig.
The effects of current on wave wavelength are shown in Fig.
We now choose the following parameters:

As an example, consider currents of C0 = ±0.6 m·s−1 and C0 = 0 m·s−1 on linear and nonlinear fractal sea surfaces respectively. The wave height evolutions with time are shown in Fig.
Results in Fig.
The values of kurtosis (β) and skewness (α) of the wave height PDF of the fractal sea affected by different current velocities in Fig.
| Table 1. Values of kurtosis and skewness of PDF of the fractal sea surface wave height affected by different current velocities. . |
The effective trends of current on kurtosis and skewness of wave height distributions on the linear and nonlinear fractal sea surface are shown in Fig.
The results in Fig.
Results in Fig.
It is shown in both Figs.
The differences in spectrum between linear and nonlinear fractal sea surfaces, for different current velocities, are shown in Fig.
A wave–current coupled model is established in this paper. The model is used to numerically study the effect of the current on the wave.
Numerical simulation results show that the wave amplitude decreases (increases) when the wave propagates in the direction the same as (opposite to) the current direction. Wavelength and wave height kurtosis increase, whereas wave spectrum intensity decreases and shifts towards lower frequencies when current direction is parallel to the ocean wave direction. By comparison, if current direction is opposite to the the wave direction, then wave amplitude increases, wavelength and wave height kurtosis decrease, and spectrum intensity increases and shifts towards higher frequencies. The effect of ocean current is much stronger than that of a nonlinear wave. The kurtosis of the nonlinear fractal ocean surface is larger than that of the linear fractal ocean surface. The effect of current on the skewness of the probability distribution function is negligible.
Our results imply that the ocean wave spectrum distribution is changed by ocean surface currents, which must be reflected in electromagnetic backscattering observations. An electromagnetic backscatter model of the effect of current on fractal sea surface is established in Part 2 of this study, based on the wave–current coupled model presented in this paper (Part 1).
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 | |
| 18 | |
| 19 |










