Low-dimensional semiconductor systems (LDSS) and their nonlinear optical properties are of great interest because of their promising utilization and relevance in making new optical devices for the switching^[1] and antenna^[2,3] applications. It is found that higher optical transition energies do exist in LDSS. By reducing the dimensionality of nano-heterostructures, the optical, electrical, and transport properties of this system could be enhanced due to the geometrical confinement effects.

The exceptional development in the microfabrication makes it possible to produce LDSS in many laboratories and to play a critical role in microelectronic and optoelectronic devices. Some studies also reveal the atomic properties such as discrete energy levels and shell structures motivate the study of the electronic and optical properties of these nanostructures.^[4,5]

The electronic and optical properties of bulk materials also depend on the electron–photon interaction that plays a significant role and also affects the LDSS. Therefore, LDSS especially quantum dots (QDs) have been extensively investigated both theoretically and experimentally. Discrete energy levels are formed by the confinement of charge carriers (electrons and holes) of QDs in three dimensions (3D) that changes the optical properties and due to this QDs are also known as artificial atoms.^[6]

There have been many theories discussing the electronic properties of QDs. Quantum genetic algorithm,^[7] configuration interaction,^[8,9] perturbation,^[10] variational,^[11,12] density functional,^[13,14] Hartree–Fock Roothaan method,^[15] exact solution,^[16] and other theoretical methods^[17–19] have been employed to study such properties. According to these theories, electronic properties mainly depend on the shapes of these semiconductor nanocrystals, which have been observed experimentally, but precise calculations of the quantum dot (QD) structure have not yet been realized due to manufacturing imperfections resulting from the growth methods. The k.p. theory gives a complete description of the electronic structure, but its high computational requirements make it difficult to know the structure parameters. According to the literature, many analytical and numerical models have been used to research different shape QDs. For example, Jungho and Chuang^[20] offered the quantum disk model, Zhang et al.^[21] discussed cylindrical QDs, Nenad et al.^[22] presented QDs in the form of a truncated hexagonal pyramid, and cone or truncated cone dots were discussed in many studies.^[23–25] Many researchers have studied QDs in lens or dome shapes,^[26–29] the results of which are in good agreement with the experimental results (see Figs. 1(a) and 1(b)). In most of these studies, simulated results are different from the real structure and do not provide precise information about the whole QD structure as some simplifications were employed. One of such simplifications is the eigenvalue problem for a particle in the 2D system. It is assumed that the confinement of the particle to the lens or dome shape QD merely depends on the time-independent Schrödinger equation with cylindrical symmetry. A few studies used the variable separation method to separate ρ and z directions,^[26,27,29] such as in the cylindrical problem. Another study used one direction in the solution and ignored the other direction.^[23,28] None of these studies incorporated the effect of 3D geometry for lens or dome shaped QDs.

Fig. 1.

	Figure Option ViewDownloadNew Window
	Fig. 1. Cross-sectional TEM images showing lens-shaped InGaN QD ((a) Ref. [42], (b) Ref. [43]). (c) Schematic illustration of 3D lens-shaped QD grown on wetting layer (WL) inside a cubic computation domain.

This study deals with the inspection of confinement effects of QDs on the electronic and optical properties for III–nitride (III–N) materials. III–N semiconductors (InN, GaN, AlN, and their alloys) have exhibited considerable potential in developing the optoelectronic devices working in the ultra-violet and visible region, for example lasers, light emitting diodes, optical amplifiers, solar cells, and photodetectors.^[30–32] A few recent results are indicating the small band-gap (∼ 0.7 eV) of InN.^[33–35] This shows that the bandgap of ternary alloy InGaN could cover the whole solar spectrum, i.e., from infrared to ultraviolet. This exclusive bandgap span of nitride-based materials is very crucial in fabricating high-efficiency (50%) multijunction solar cells and full-spectrum devices.^[36] Currently, the devices based on III–nitrides are fabricated by using metal–organics chemical vapor deposition (MOCVD), metal–organic–vapor phase epitaxy (MOVPE), and molecular beam epitaxy (MBE) techniques.^[37–40]

The InGaN alloy is a major player in the recent development of optoelectronics and high-power as well as high-temperature devices. Particularly, this material exhibits promising applications for future multi-layers solar cells with high efficiency,^[38,41] and has also shown a higher degree of resistance to radiation damage compared to other photovoltaic materials.^[37] It offers a flexible choice of the band gap energies and a number of the component junctions. Technologically, this would be very important as relatively few precursors are needed to grow different junctions. From III–N group, researchers have not only significantly investigated GaN but also have reasonably developed it, whereas, with reference to the photovoltaic application, the lower band gap InGaN is more practical and yet is a subject of fundamental research.

The optical interband and intersubband (intraband) transitions are the most interesting characteristics of QDs. Furthermore, the linear and the third-order nonlinear optical absorption coefficients (ACs) greatly affect the optoelectronic device applications, such as optical amplifiers, photodetectors, and solar cells. Hence, in recent years, the nonlinear optical properties of QDs are the center of interest for both fundamental and applied research due to large values of the dipole moment matrix elements that attain both linear and nonlinear optical properties, and large value of oscillator strength function. Bouzaïene et al.^[27] have studied nonlinear optical rectification of lens-shaped InAs QDs inside a large cylinder of GaAs. Within the same assumptions, Khaledi–Nasab et al.^[28] have investigated the effect of Woods–Saxon (WS) potential on the electronic structure of InAs QDs, which leads to strong alterations in linear susceptibility and group velocity.

All the previous studies were in 2D and unable to explain the real system. To model an appropriate optical device close to reality, the investigation of electronic and optical properties of the 3D system is imperative. To the best of our knowledge, up till now, the linear and third-order nonlinear optical absorption coefficient for interband and intraband transitions of 3D lens-shaped QDs has not been studied.

The focus of this article is to investigate linear and nonlinear optical ACs in different sizes of lens-shaped QDs. Firstly, we calculated the ground state and the first excited state energies and their corresponding wave functions of the QD system with and without strain effect. Calculations were performed using 3D finite element method (FEM). The linear, third-order nonlinear, and total optical ACs as a function of incident photon energy with size and In-composition effect were also studied.

In order to probe semiconductor QDs’ properties with lens-shaped QDs, the effective mass approximation (EMA) of one-band Schrödinger equation for electrons (holes) in conduction (valence) bands has been employed as

Figure 1(c) shows a schematic illustration of 3D lens-shaped QD grown on wetting layer (WL) inside a cubic computation domain. In this system, three types of physical boundary conditions can be classified. Dirichlet boundary condition (Ψ = 0) is applied on the top and bottom boundaries (I and II). Meanwhile, the Neumann boundary condition (n̂, · ∇Ψ = 0) is used to the four side boundaries (III). Finally, the periodic boundary conditions are assumed for internal interface boundaries (IV and V) of InGaN and GaN because of the potential finiteness and the envelope function continuity.

In this study, we are interested in wurtzite (W) structure as its hexagonal structure is more stable than the zinc-blend. The strain effect is calculated to figure out the changes in the confinement energy for both electrons and holes. Due to strain, there is an energy shifting for the conduction and valence band edges as^[30]

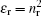
Firstly, conduction and valence subbands are treated for In_xGa_1−xN/GaN lens-shaped QD with a base diameter ranging from 8 nm to 30 nm, height variation from 2 nm to 13 nm, and in all calculations 2-nm thickness of WL is also assumed, as in the previous experiments.^{[39,43,46,47]} The other related parameters (at room temperature) used in the calculation are listed in Table 1.

Table 1.

Table 1.

Table 1. Material parameters of wurtzite III-nitride semiconductors.[48,49] . Parameter Notation Unit InN GaN InxGa1−xN Electron effective mass me kg 0.22mo (0.22 − 0.11x)mo Hole effective mass mh kg 0.5mo 0.8mo (0.8 − 0.3x)mo Lattice constant a Å 3.545 3.189 3.189 + 0.356x Band gap energy Eg eV 0.608 3.437 3.437 − 4.259x + 1.43x2 Electrical permittivity εr – 15 9.6 9.6 + 5.4x Refractive index – 3.87 3.09 3.09 + 0.78x Elastic constant C13 GPa 92 106 106 − 14x Elastic constant C33 GPa 224 398 398 − 174x Conduction-band hydrostatic deformation potential ac eV –2.65 –6.71 4.06x − 6.71 Valence-band deformation potential D1 eV –3.6 –3.6 –3.6 Valence-band deformation potential D2 eV 1.7 1.7 1.7 Valence-band deformation potential D3 eV 5.2 5.2 5.2 Valence-band deformation potential D4 eV –2.7 –2.7 –2.7 a mo = free electron mass.

Table 1. Material parameters of wurtzite III-nitride semiconductors.[48,49] .

The Schrödinger equation (Eq. (1)) is numerically solved by FEM. For electron and hole, the eigenvalues and envelope functions are obtained as quantum confinement energies for two first states separately. The strain effect of In_xGa_1−xN QD on GaN WL as a function of In-composition is shown in Table 2. The band gap of In_xGa_1−xN increases enormously due to compressive strain and causes a change in the confined energy levels of QDs. The difference between strained and unstrained band gap energy also reduces with the decrease of the In-fraction in In_xGa_1−xN material. This is accredited to the QDs’ materials and unstrained GaN becoming similar, and thus reduces the strain effect. As it is shown in Table 2, this fact is very clear at the point x = 0.3 and due to strain the energy level at both s- and p-states increases nearly 0.3 eV. It is important to mention here that Coulomb-coupling interaction, piezoelectric and spontaneous polarization energy are not incorporated in the present calculations because they do not have a dramatic influence on the QDs as their QDs size is very small.^[50]

Table 2.

Table 2.

Table 2. Conduction and valence subbands for InxGa1−xN/GaN unstrained structure with the change of In-content in QD, and 30-nm base diameter, 2-nm QD height and WL. . Unstrained Strained x Conduction subbands/eV Valence subbands/eV Conduction subbands/eV Valence subbands/eV s-states p-states s-states p-states s-states p-states s-states p-states 0.1 3.090312 3.102728 0.021158 0.025076 3.192378 3.204794 0.053302 0.057220 0.2 2.723315 2.738358 0.025289 0.029848 2.911848 2.926891 0.090243 0.094802 0.3 2.379786 2.396626 0.028002 0.032991 2.639348 2.656188 0.126532 0.131521 0.4 2.063208 2.081613 0.030236 0.035589 2.378558 2.396963 0.163228 0.168581 0.5 1.774666 1.794580 0.032275 0.037968 2.130803 2.150717 0.200767 0.206460 0.6 1.514667 1.536119 0.034245 0.040273 1.896885 1.918337 0.239456 0.245484 0.7 1.283517 1.306588 0.036216 0.042584 1.677483 1.700554 0.279599 0.285967 0.8 1.081439 1.106256 0.038233 0.044957 1.473291 1.498108 0.321531 0.328255 0.9 0.908626 0.935358 0.040333 0.047430 1.285109 1.311841 0.365667 0.372764

Table 2. Conduction and valence subbands for InxGa1−xN/GaN unstrained structure with the change of In-content in QD, and 30-nm base diameter, 2-nm QD height and WL. .

Cross-section distributions for s- and p-state envelope functions are illustrated in Figs. 2 and 3, for several QD sizes. In Fig. 2, s-state envelope function covers the central part of lens-shaped QD with a low percentage of overlapping with the WL, and it is decreasing with the increase of the QD height while the p-state envelope functions show a dumbbell-like distribution with more tendency to overlap with WL than s-state.

Fig. 2.

	Figure Option ViewDownloadNew Window
	Fig. 2. Cross sections of s- and p-states for In0.6Ga0.4N/GaN envelope function with 20 nm diameter, 2 nm WL and different QD heights: (a) 4 nm, (b) 8 nm, and (c) 12 nm.

Fig. 3.

	Figure Option ViewDownloadNew Window
	Fig. 3. Cross section of s- and p-states for In0.6Ga0.4N/GaN envelope function with 3 nm QD height, 2 nm WL, and different base diameters: (a) 10 nm, (b) 20 nm, and (c) 30 nm.

A comparison between Figs. 2 and 3 shows that the change in QD height is more effective than the base diameter, and the envelope function tends to be more confined inside QD. This behavior explains why the electron energy of s- and p-states changes by 0.1 eV and 0.11 eV, respectively, and the hole energy of s- and p-states changes by 0.04 eV for both strained and unstrained structures, when QD height changes from 2 nm to 13 nm (Fig. 4). In Fig. 5, QD base diameter changes from 8 nm to 30 nm, the electron energy of s- and p-states changes by 0.06 eV and 0.14 eV respectively for both strained and unstrained structures. The hole energy of s- and p-states changes by 0.02 eV and 0.04 eV, respectively, for both strained and unstrained structures.

Fig. 4.

	Figure Option ViewDownloadNew Window
	Fig. 4. The electron (a) and hole (b) energy of s-states (square) and p-states (circle) for In0.6Ga0.4N/GaN as a function of QD height with 20 nm QD base diameter and 2 nm WL.

Fig. 5.

	Figure Option ViewDownloadNew Window
	Fig. 5. The electron (a) and hole (b) energy of s-states (square) and p-states (circle) for In0.6Ga0.4N/GaN as a function of QD base diameter with 3 nm QD height and 2 nm WL.

After calculating conduction and valence subbands as well as the envelope functions corresponding to the s- and p-state configurations, the optical ACs of s–s, p–p, and all transitions between these energy states are shown in Figs. 6 and 7. In this part, we employed the following parameters, ε_r = 9.6 + 5.4x that is the electrical permittivity of the semiconductor In_xGa_1−xN QD, the relaxation time τ = 0.045 ps. In order to investigate the influence of In-composition on ACs, we plotted the linear, nonlinear, and total ACs of the s–s, p–p, and all transitions between two states as a function of photon energy for four different values of x-mole fraction (Figs. 6 and 7). Figure 6 reveals that the ACs of the p–p transition have an amplitude greater than these of the s–s transition. This is also evident from the figures that the peak positions of ACs are the same. Figure 7 displays a very important feature. It shows that the peak positions of ACs from interband and intraband transitions are shifting toward lower photon energy, i.e., the red-shift, and also the amplitudes of ACs decrease when the In-composition increases. These figures reveal that In_xGa_1−xN/GaN with x ≥ 0.5 is a good LDSS for solar cell devices, and the best for lasers at longer wavelengths. The theoretical predictions obtained here are in good agreement with the experimental results.^[51,52]

Fig. 6.

	Figure Option ViewDownloadNew Window
	Fig. 6. The absorption coefficient from interband (a) s–s state and (b) p–p state transition as a function of photon energy for InxGa1−xN / GaN strained structure with 30 nm base diameter, 2 nm QD height and WL, at optical intensity of 15 MW/m2.

Fig. 7.

	Figure Option ViewDownloadNew Window
	Fig. 7. The absorption coefficient from interband and intraband transitions as a function of photon energy for InxGa1−xN / GaN strained structure with 30 nm base diameter, 2 nm QD height and WL, at optical intensity of 15 MW/m2.

The change in the peak positions of photon energy and amplitudes of ACs is obvious when the height of QD is varied from 4 nm to 12 nm (Fig. 8). One can see that the total optical ACs of QD for small values of dot height are much stronger than those having large values. The physical reason is that the amplitude of the optical ACs strongly depends on the electron density in QDs, i.e., it is reverse proportional to the volume of QD (V_QD). In addition, we found that the absorption peaks shift towards the red as the QD height increases. With the QD height changing, there is a large overlapping between s- and p-energy states that means that the change in the state energy is small (Fig. 4), due to this overlapping, one peak for total, linear and nonlinear ACs (Fig. 8). Figure 9 displays the optical ACs as a function of photon energy with different values of QD base diameter. This can be clearly seen in these figures that the amplitudes of total, linear and nonlinear ACs decrease prominently with the increase of QD base diameter. Similar behavior has been found above for the variation of QD height. In addition, the red shift in the absorption peaks is noted when the base diameter of QD increases. The difference between energy states is very clear when QD base diameter decreases (similar behaviour is seen in Fig. 5), which induced the optical absorption spectrum separated into two main peaks at small values of QD base diameter (Fig. 9). Here, it is worth remembering that the changing in QD height has more effect than the QD base diameter on the amplitudes of ACs; mainly this effect comes from the contribution for height in volume calculation of QD. According to these results, by controlling the height of QDs in growth process only, and making it the smallest, one would fabricate optical devices with high absorption.

Fig. 8.

	Figure Option ViewDownloadNew Window
	Fig. 8. The absorption coefficient from interband and intraband transitions as a function of photon energy for In0.6Ga0.4N/GaN strained structure with 20 nm base diameter, 2 nm WL, and different QD heights: (a) 4 nm, (b) 8 nm, and (c) 12 nm, at optical intensity of 15 MW/m2.

Fig. 9.

	Figure Option ViewDownloadNew Window
	Fig. 9. The absorption coefficient from interband and intraband transitions as a function of photon energy for In0.6Ga0.4N/GaN strained structure with 3 nm QD height, 2 nm WL, and different base diameters: (a) 10 nm, (b) 20 nm, and (c) 30 nm, at optical intensity of 15 MW/m2.

To understand the relation between the incident optical intensity (I) and the absorption spectrum, ACs with four values of optical intensity are illustrated in Fig. 10. The peak value of the total AC decreases with the increase of the incident optical intensity that comes from the negative increasing contribution of the third-order nonlinear optical AC, which strongly depends on incident optical intensity. This fact was also verified experimentally.^[53] However, there is no shift in the peak position with the change of the incident optical intensity. This leads to taking into consideration the third-order nonlinear term in the calculation of the total optical AC, especially with high optical intensity.

Fig. 10.

	Figure Option ViewDownloadNew Window
	Fig. 10. The absorption coefficient from interband and intraband transitions as a function of photon energy for In0.6Ga0.4N/GaN strained structure with 2 nm QD height, 30 nm base diameter, and 2 nm WL, at four values of optical intensity: (a) 5 MW/m2, (b) 10 MW/m2, (c) 15 MW/m2, and (d) 20 MW/m2.

In this work, electronic structures of InGaN/GaN lens-shaped QDs were numerically investigated within the framework of Schrödinger equation for envelope function in the effective mass approximation by using FEM. The linear and nonlinear optical ACs were calculated. Our results showed that by decreasing In-concentration of InGaN QDs, the amplitudes of linear and nonlinear absorption coefficients increase. In addition, it has been found that increasing QD size causes a red shift and reduces the amplitudes of total, linear and nonlinear ACs, especially QD height is more effective. Furthermore, we have calculated the total optical AC, and found that it is essential to consider the nonlinearity part particularly with high values of optical intensity. The present results are of great impact and can be used for the improvement of optical devices. These results would be important for applications based on the nonlinear optical properties. This theoretical work may provide the basis for profound outcomes for practical applications of optoelectronic devices.